二進制與十進制的區別在于數碼的個數和進位規律有很大的區別
,顧名思義,二進制的計數規律為逢二進一,是以2為基數的計數體制。10這個數在二進制和十進制中所表示的意義完全不同,在十進制中就是我們通常所說的十,在二進制中,其中的一個意義可能是表示一個大小等價于十進制數2的數值。
仿照例題1.3.1,我們可以將二進制數10表示為:10=1×21+0×20
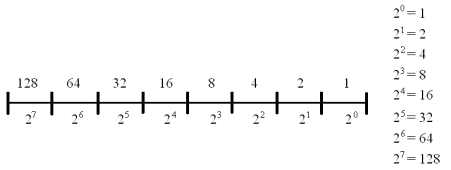
圖1.3.2 二進制數的位權圖
一般地,任意二進制數可表示為:
例題 1.3.2 試將二進制數(01010110)B轉換為十進制數。
解:將每一位二進制數乘以位權后相加便得相應的十進制數

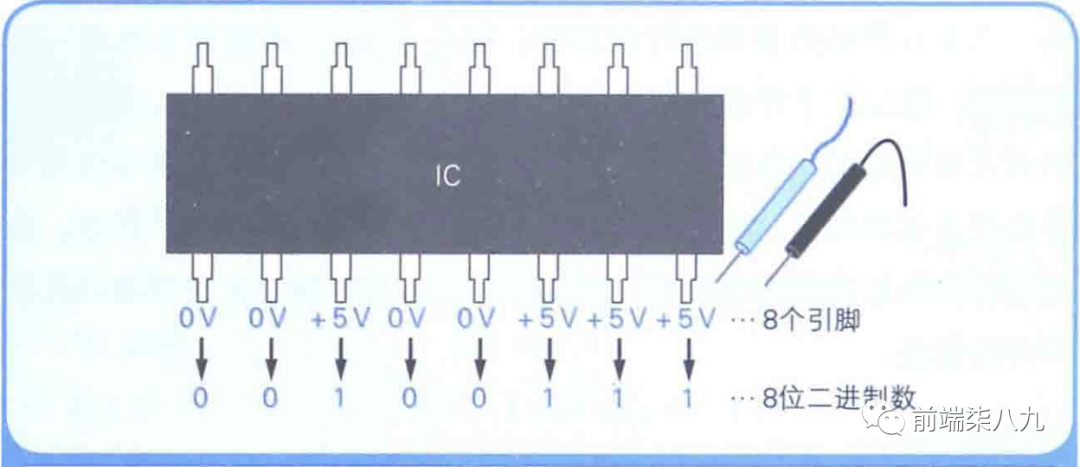
在數字電子技術和計算機應用中,二值數據常用數字波形來表示
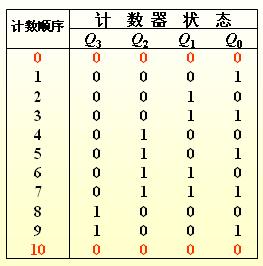
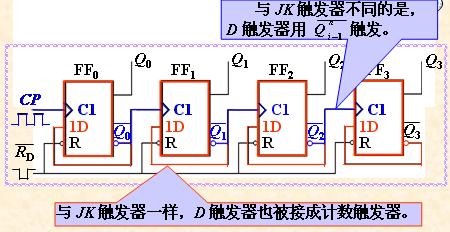
。使用數字波形可以使得數據比較直觀,也便于使用電子示波器進行監視。圖1.3.3表示一計數器的波形。
 圖1.3.3 用二進制數表示0~15波形圖
圖1.3.3 用二進制數表示0~15波形圖
圖中給出了四個二進制波形。看這種二進制波形圖時,我們應當沿著圖中虛線所示的方向來看,即使圖中沒有標出虛線(一般都沒有標出),也要想象出虛線來。其中在每一個波形上方的數字表示了與波形對應的位的數值,最后一行則是相應的十進制數 ,其中LSB是英文Least Significant Bit的縮寫,表示最低位,MSB是Most Significant Bit的縮寫,表示二進制數的最高位。顯然,這是一組4位的二進制數,總共有16組,最左邊的二進制數為0000,最上邊的波形代表二進制數的最低位,也就是通常在十進制數中我們所說的個位數,最下面的是最高位。圖中最右邊的二進制數為1111,對應的十進制數為15。再來看看對應于十進制數5的二進制數是多少呢?是0101,對了,讀數的順序是從下往上。
二進制數在數字系統(比如計算機之間)中的傳輸的方式分為串行和并行兩種。
其中串行傳輸時二進制數是按照逐位傳遞的方式進行傳輸,根據實際情況可以從最高位或最低位開始傳輸,一般情況下是從最高位開始傳輸的。只需要一根數據線。如圖1.3.4所示,要完成八位二進制數的傳輸,需要經歷八個時鐘周期。

圖1.3.4 二進制數據的串行傳輸
(a) 兩臺計算機之間的串行通信 (b) 二進制數據的串行表示
典型的例子是調制解調器與計算機之間的通信就是通過串行傳輸來完成的。
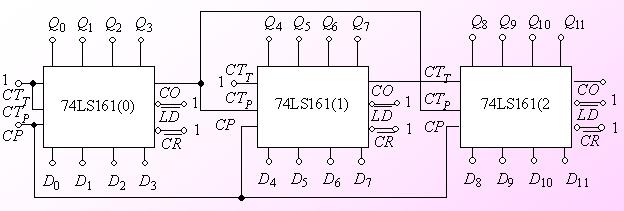
并行傳輸的效率要高于串行傳輸,一次可以傳輸完整的一組二進制數。但是根據所要傳輸的二進制數的位數的多少,需要備足足夠多的數據線。一般來說,常見的并行傳輸采用的數據線有8、16、32等,再多就很少見了。典型的并行傳輸例子是打印機與計算機之間的通信傳輸,見圖1.3.5。

(a)

(b)
圖1.3.5 并行傳輸數據的示意圖
(a) 計算機與打印機之間的并行通信 (b) 二進制數據的并行表示
圖1.3.5顯示了采用并行傳輸模式,只需要一個時鐘周期,即可完成八位二進制數的傳輸。
二進制的優點:
數字裝置簡單可靠,所用元件少;
只有兩個數碼0和1,因此它的每一位數都可用任何具有兩個不同穩定狀態的元件來表示;
基本運算規則簡單,運算操作方便。
二進制的缺點:
用二進制表示一個數時,位數多;
例如:(49)D=(110001)B;
因此實際使用中多采用送入數字系統前用十進制,送入機器后再轉換成二進制數,讓數字系統進行運算,運算結束后再將二進制轉換為十進制供人們閱讀;這就引出了十-二進制之間的轉換問題。
 電子發燒友App
電子發燒友App












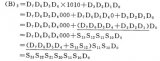

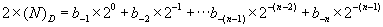











評論