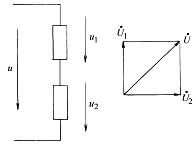
正弦量除了用波形和瞬時表達式來表示以外,利用歐拉公式還可以表示成復指數的形式。一個正弦交流電流![]() ,可以表示為復指數形式:
,可以表示為復指數形式:
![]() (3-3-1)
(3-3-1)
方括號內是一個復數,符號Im表示取復數的虛部。復指數的模即為正弦函數的幅值![]() ,
,

圖3-3-1
幅角為正弦函數的相位![]() ,它隨時間以角度
,它隨時間以角度![]() 增長。若把復數
增長。若把復數![]() 在復平面上的對應點與原點之間用一帶箭頭的有向線段相連,如圖3-3-1所示,則可得到一個幅角隨時間變化的旋轉矢量。這條用來表示正弦函數的矢量稱為正弦量的相量。相量在復平面上的圖形稱為相量圖。圖中畫出了該相量在
在復平面上的對應點與原點之間用一帶箭頭的有向線段相連,如圖3-3-1所示,則可得到一個幅角隨時間變化的旋轉矢量。這條用來表示正弦函數的矢量稱為正弦量的相量。相量在復平面上的圖形稱為相量圖。圖中畫出了該相量在![]() 和
和![]() 時的位置。當
時的位置。當![]() 時,該相量與實軸夾角為正弦函數的初始相位角
時,該相量與實軸夾角為正弦函數的初始相位角 。該相量
。該相量 以角速度隨時間向逆時針方向旋轉,當
以角速度隨時間向逆時針方向旋轉,當![]() 時刻,相量轉到圖中虛線所示位置。此時與實軸夾角為
時刻,相量轉到圖中虛線所示位置。此時與實軸夾角為![]() 。由圖可以看出,該相量在虛軸上的投影長度等于
。由圖可以看出,該相量在虛軸上的投影長度等于![]() ,即等于對應的正弦函數在該時刻的瞬時值。
,即等于對應的正弦函數在該時刻的瞬時值。
在用復平面上的相量表示正弦函數時,只要確定其初相位時的相量即可,即相當于取![]() 時的復指數函數
時的復指數函數![]() 。實際的正弦時間函數只要把該復數乘以
。實際的正弦時間函數只要把該復數乘以![]() ,再取其虛部就可以得到。在電工計算中,復數中的模一般取為正弦量的有效值,即可以把復數表示為
,再取其虛部就可以得到。在電工計算中,復數中的模一般取為正弦量的有效值,即可以把復數表示為![]() ,這里I為有效值,
,這里I為有效值, 為初相角。這樣我們可以把式(3-1-1)的正弦交流電流表示成相量形式為
為初相角。這樣我們可以把式(3-1-1)的正弦交流電流表示成相量形式為
![]() ?? (3-2-2) 或 ?
?? (3-2-2) 或 ?![]() ??(3-2-3)
??(3-2-3)
掌握正弦函數的瞬時值表達式,相量表示圖形和復數表達式,并理解它們之間的內在轉換關系和意義,是穩態正弦交流電路中相量計算的基礎。

圖? 3-3-2
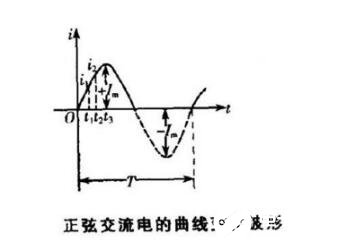
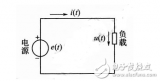
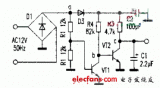
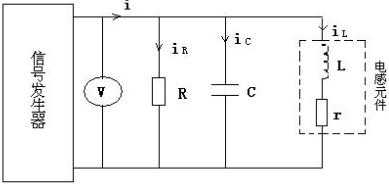
下面來討論兩個同頻率正弦量的計算問題。對于圖3-3-2所示的電路,若已知兩條支路中的電流為
![]() ,
,![]()
則合成電流i為:![]()
由前面分析得:
![]()
![]()
![]()
![]()
這里:![]() ? (3-3-4)
? (3-3-4)
由上式可知,要計算合成電流i只要知道合成電流的相量 即可,于是兩個同頻率的正弦電流相加問題,就轉化成這兩個正弦電流對應的相量的相加問題,即把三角函數的相加轉化為兩個復數的相加運算。
即可,于是兩個同頻率的正弦電流相加問題,就轉化成這兩個正弦電流對應的相量的相加問題,即把三角函數的相加轉化為兩個復數的相加運算。
我們還可以在相量圖上直觀地來分析兩個正弦量的相量相加的意義。電流i1與i2的相量 、
、 示于圖3-3-3中。
示于圖3-3-3中。
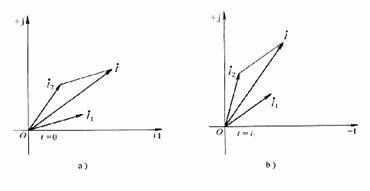
圖? 3-3-3
當![]() 時相量處于初始位置。按兩個相量相加的平行四邊形法則,作
時相量處于初始位置。按兩個相量相加的平行四邊形法則,作 與
與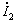 的合成相量
的合成相量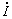 ,如圖3-3-3b所示。由圖可見
,如圖3-3-3b所示。由圖可見 在虛軸上的投影即為
在虛軸上的投影即為 與
與 相量在虛軸上的投影值之和,合成相量
相量在虛軸上的投影值之和,合成相量 在虛軸上的投影即為
在虛軸上的投影即為![]() 的瞬時值。經過時刻
的瞬時值。經過時刻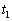 ,相量
,相量 與
與 都沿著逆時針方向旋轉了
都沿著逆時針方向旋轉了![]() 角度,如圖3-3-3a所示,由于
角度,如圖3-3-3a所示,由于 與
與 的相對位置沒有變化,因此其合成相量
的相對位置沒有變化,因此其合成相量 的長度也沒有變化。與
的長度也沒有變化。與![]() 時刻相比,
時刻相比, 也逆時針旋轉了
也逆時針旋轉了![]() 相角。此時
相角。此時 與
與 在虛軸上的投影值之和仍等于合成相量在虛軸上的投影。在任意時刻都可以用合成相量
在虛軸上的投影值之和仍等于合成相量在虛軸上的投影。在任意時刻都可以用合成相量 在虛軸的投影來表示
在虛軸的投影來表示 與
與 的投影之和。相量在虛軸的投影即為該相量對應的正弦函數的瞬時值,這樣兩個正弦函數瞬時值相加之和就等于合成相量所表示的正弦函數瞬時值,從而把三角函數運算變成為相量相加減的復數運算。必須指出,只有同頻率的
的投影之和。相量在虛軸的投影即為該相量對應的正弦函數的瞬時值,這樣兩個正弦函數瞬時值相加之和就等于合成相量所表示的正弦函數瞬時值,從而把三角函數運算變成為相量相加減的復數運算。必須指出,只有同頻率的
正弦量才可以進行相量運算。
圖? 3-3-4
例3-3-1?? 在圖3-3-4中,已知![]() ,
,![]() ,試求總電壓u的值。
,試求總電壓u的值。
解:根據基爾霍夫定律有![]() ,用相量來表示則
,用相量來表示則![]() ,已知
,已知![]() ,
,![]() ,則可求得
,則可求得
![]()
總電壓u的瞬時表達式為:![]()
 電子發燒友App
電子發燒友App














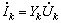
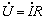
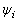












評論