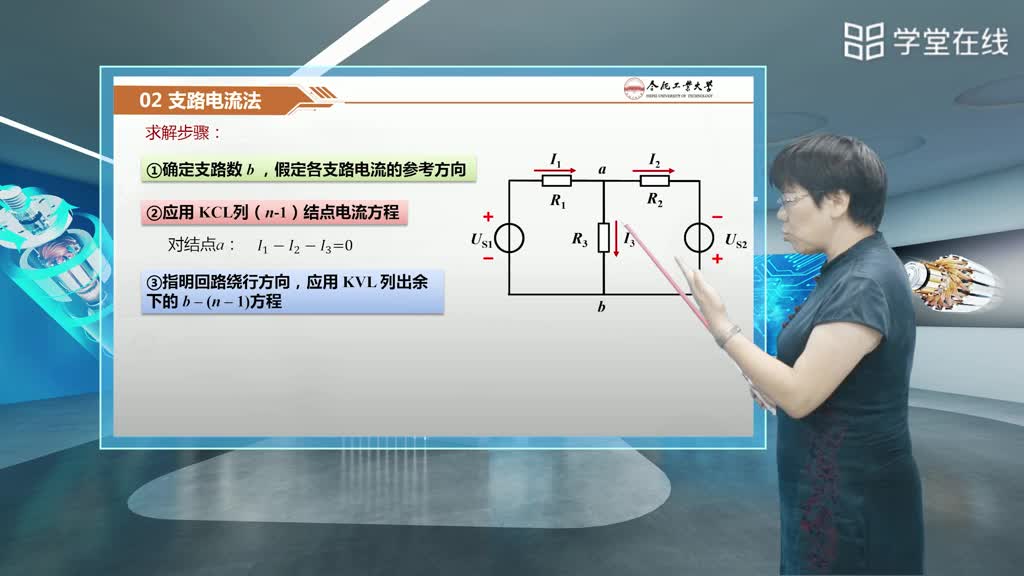
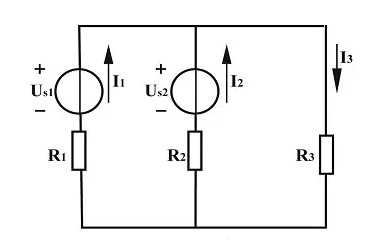
以支路電流作為電路變量,根據KCL,KVL建立電路方程,聯(lián)合求解電路方程從而解出各支路電流的電路分析方法,稱為支路電流法。
如圖2-2-1所示,已知:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,現要求
,現要求![]() 和
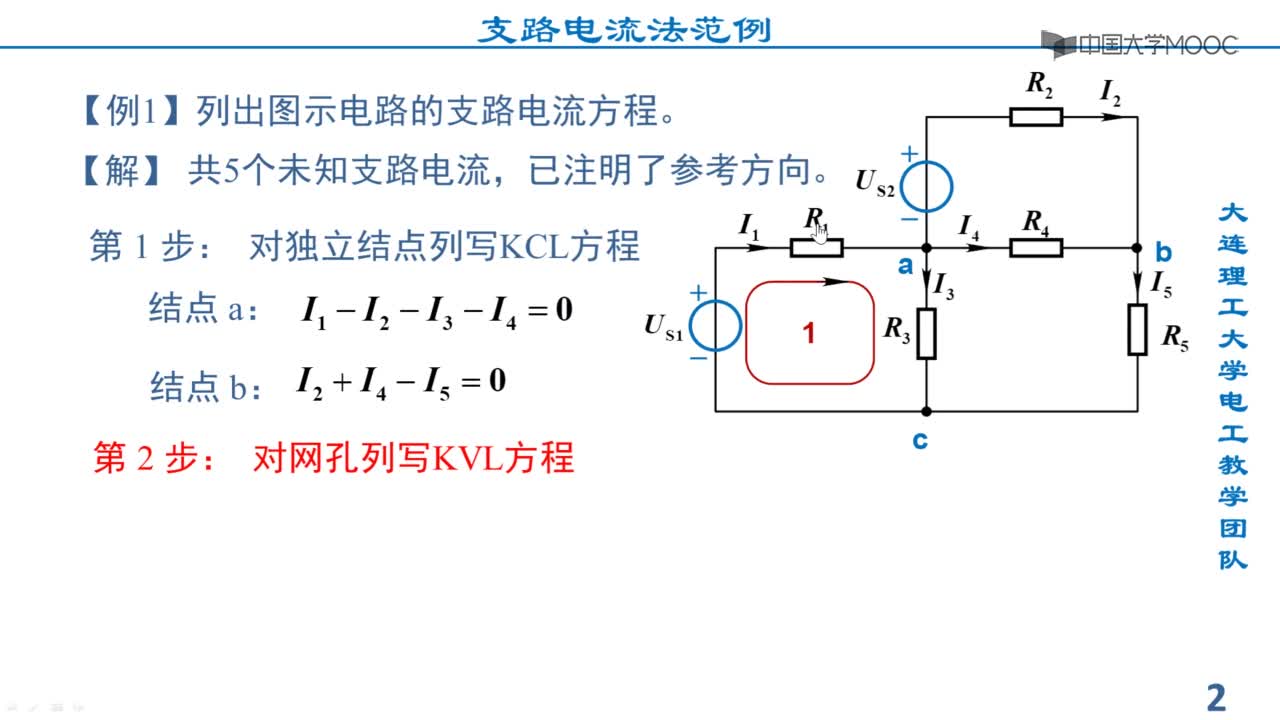
和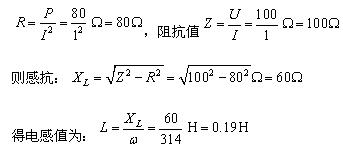 ,如圖選擇各支路電流參考方向。根據基爾霍夫電流定律有:
,如圖選擇各支路電流參考方向。根據基爾霍夫電流定律有:

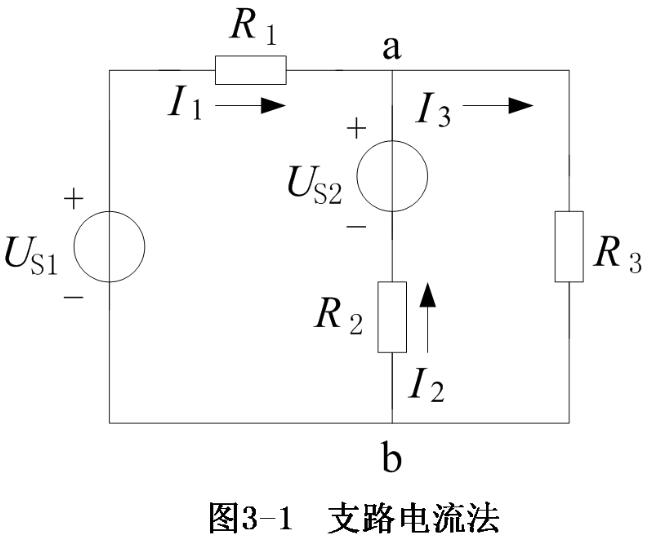
圖2-2-1
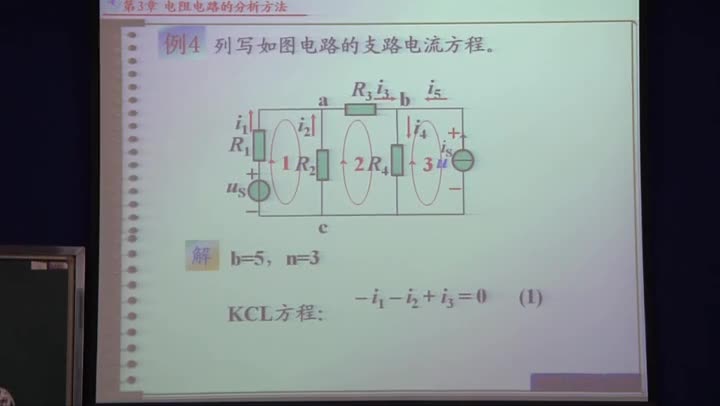
節(jié)點a: ![]() (式2-2-1),? 節(jié)點b:
(式2-2-1),? 節(jié)點b: ![]() (式2-2-2)
(式2-2-2)
顯然,(式2-2-1)與(式2-2-2)是彼此不獨立的兩個方程。
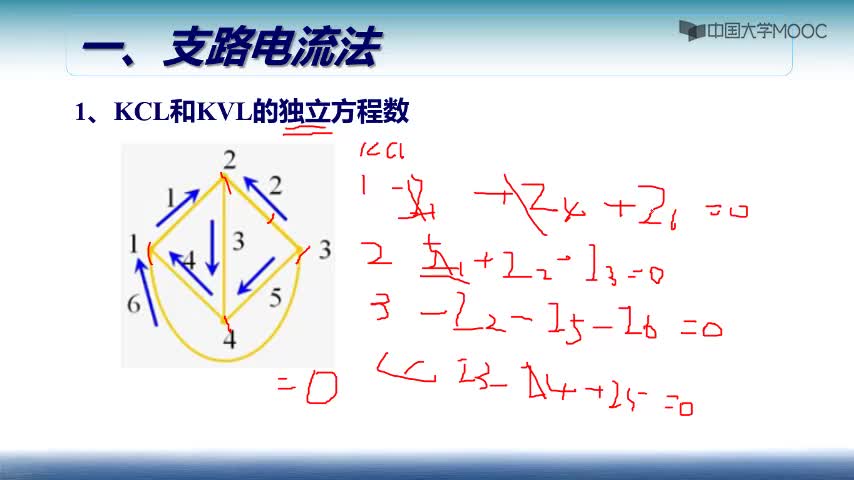
一個節(jié)點數為n,支路數為b的電路,它的獨立的節(jié)點電流方程數為![]() 。獨立節(jié)點電流方程對應的節(jié)點稱為獨立節(jié)點。那么,電路的獨立節(jié)點數為
。獨立節(jié)點電流方程對應的節(jié)點稱為獨立節(jié)點。那么,電路的獨立節(jié)點數為![]() 。
。
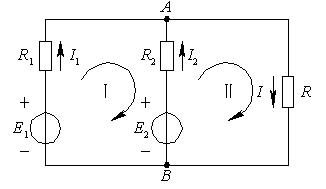
就象所有節(jié)點的KCL方程不彼此獨立一樣,所有回路的KVL方程也不彼此獨立。如圖2-2-1,![]() 是三個回路,如果分別對這三個回路列寫KVL方程,有:
是三個回路,如果分別對這三個回路列寫KVL方程,有:
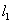 回路:?
回路:? ![]() ?????(式2-2-3)
?????(式2-2-3)
 回路:?
回路:? ![]() ?????????(式2-2-4)
?????????(式2-2-4)
 回路:?
回路:? ![]() ??????????(式2-2-5)
??????????(式2-2-5)
(式2-2-3)加上(式2-2-4)就等于(式2-2-5)。三個回路的基爾霍夫電壓定律方程不相互獨立。為此,求解前應首先選擇樹,例如圖2-2-1,選擇 所在支路為樹支(用粗線條表示),
所在支路為樹支(用粗線條表示),![]() 所在支路則為連支,這樣就可以畫出兩個基本回路(獨立回路),此時的基本回路正好是兩個網孔,也就是上述的
所在支路則為連支,這樣就可以畫出兩個基本回路(獨立回路),此時的基本回路正好是兩個網孔,也就是上述的 回路與
回路與 回路。(式2-2-3)與(式2-2-4)相互獨立。對于基本回路列寫的KVL方程,必定彼此間相互獨立。
回路。(式2-2-3)與(式2-2-4)相互獨立。對于基本回路列寫的KVL方程,必定彼此間相互獨立。
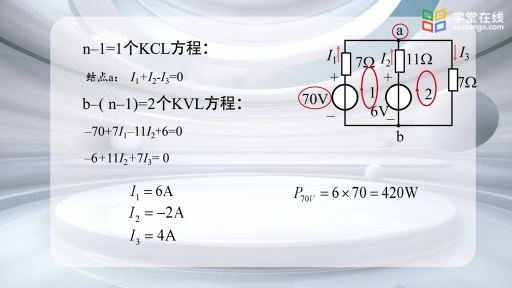
如果將圖2-2-1中![]() 所在支路改換為一個電流源,即成為圖2-2-2。若以電流源
所在支路改換為一個電流源,即成為圖2-2-2。若以電流源![]() 所在支路為樹支(用粗線條表示),可畫出兩個單連支回路
所在支路為樹支(用粗線條表示),可畫出兩個單連支回路![]() ,由支路電流法得到3個方程如下:
,由支路電流法得到3個方程如下:
![]() ?
?![]() ,
, :
:![]() ,
, :
:![]()

圖2-2-2
還有: ![]() ,從以上方程組可以解出
,從以上方程組可以解出![]() 與
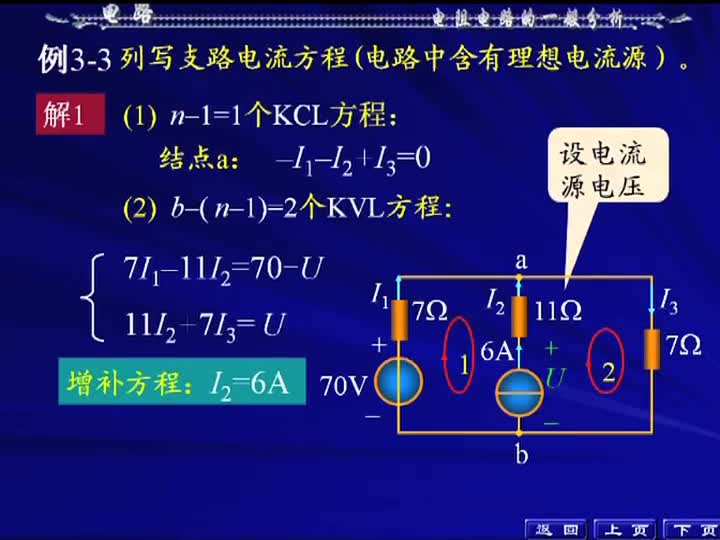
與![]() 。我們發(fā)現如此取樹后,兩個獨立回路均含有電流源所在支路,而對于含有電流源的回路列寫KVL方程時,會不可避免地引入新的未知量,即電流源兩端的電壓,從而增加了方程數目,使求解過程更加繁瑣。因此,在取樹時,應盡可能將電流源所在支路置于連支上,對于以電流源為連支的獨立回路不去列寫它的KVL方程,而代之以電流源所在支路電流就等于該電流源電流的方程。具體求解過程如下:以
。我們發(fā)現如此取樹后,兩個獨立回路均含有電流源所在支路,而對于含有電流源的回路列寫KVL方程時,會不可避免地引入新的未知量,即電流源兩端的電壓,從而增加了方程數目,使求解過程更加繁瑣。因此,在取樹時,應盡可能將電流源所在支路置于連支上,對于以電流源為連支的獨立回路不去列寫它的KVL方程,而代之以電流源所在支路電流就等于該電流源電流的方程。具體求解過程如下:以![]() 所在支路為樹(用粗線條表示),如圖2-2-3所示,畫出兩個獨立回路,則有:
所在支路為樹(用粗線條表示),如圖2-2-3所示,畫出兩個獨立回路,則有:![]() :
: ![]() ,
, 
![]() ,
,![]()
![]()

圖2-2-3
?
?????????????????????
?????? 當電路中含有電流源的個數越多,這樣選樹求解的優(yōu)越性越明顯。
?????? 在圖2-2-3中,若將電流源![]() 所在支路改換為一個受控源,如圖2-2-4所示。對于含有受控源的電路,列寫方程的原則為:首先將受控源視為獨立源列寫相應方程,然后再增加相應附加方程,用以建立控制量與方程變量間的關系。選
所在支路改換為一個受控源,如圖2-2-4所示。對于含有受控源的電路,列寫方程的原則為:首先將受控源視為獨立源列寫相應方程,然后再增加相應附加方程,用以建立控制量與方程變量間的關系。選![]() 所在支路為樹,有:
所在支路為樹,有:
![]() :
:![]() ,
,
![]() ,
,![]()
![]()
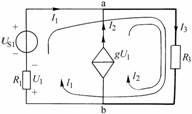
圖2-2-4
附加方程: ![]()
從上面的方程組就可以求解出![]() 和
和 。
。
 電子發(fā)燒友App
電子發(fā)燒友App




















































































評論