前面章節中已對直流電路與正弦交流電路的分析計算方法作了詳細介紹,當電路的激勵源為直流或正弦交流電源時,可用所述方法對電路進行分析計算。但是在實際電氣系統中,卻經常會遇到非正弦的激勵源問題,例如電力系統的交流發電機所產生的電動勢,其波形并非理想的正弦曲線,而是接近正弦波的周期性波形。即使是正弦激勵源電路,若電路中存在非線性器件時,也會產生非正弦的響應。在電子通信工程中,遇到的電信號大都為非正弦量,如常見的方波、三角波、脈沖波等,有些電信號甚至是非周期性的。
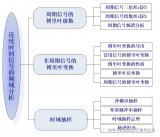
對于線性電路,周期性非正弦信號可以利用傅里葉級數展開把它分解為一系列不同頻率的正弦分量,然后用正弦交流電路相量分析方法,分別對不同頻率的正弦量單獨作用下的電路進行計算,再由線性電路的疊加定理,把各分量疊加,得到非正弦周期信號激勵下的響應。這種將非正弦激勵分解為一系列不同頻率正弦量的分析方法稱為諧波分析法。
設周期函數的周期為T,則有:
![]() ?? (k為任意整數)
?? (k為任意整數)
如果函數滿足狄里赫利條件,那么它就可以分解成為傅里葉級數。一般電工技術中所涉及的周期函數通常都能滿足狄里赫利條件,能展開為傅里葉級數,在后面討論中均忽略這一問題。
對于上述周期函數,可表示成傅里葉級數:
![]() ????? ??????(6-1-1)
????? ??????(6-1-1)
或? ???????????????(6-1-2)
式中,![]() 稱為基波角頻率;二式中系數之間有關系式:
稱為基波角頻率;二式中系數之間有關系式:
或 ?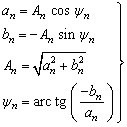 ?????????????????????????(6-1-3)
?????????????????????????(6-1-3)
展開式中除第一項外,每一項都是不同頻率的正弦量,![]() 稱為周期函數的直流分量(恒定分量),第二項
稱為周期函數的直流分量(恒定分量),第二項![]() 稱為基波分量,基波角頻率
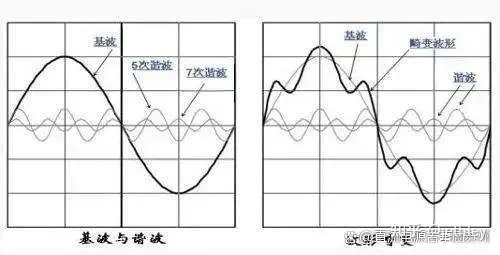
稱為基波分量,基波角頻率![]() ,其變化周期與原函數周期相同,其余各項(的項)統稱為高次諧波。高次諧波分量的頻率是基波頻率的整數倍。當時稱為二次諧波,時稱為三次諧波等等。是第n次諧波的初相角。
,其變化周期與原函數周期相同,其余各項(的項)統稱為高次諧波。高次諧波分量的頻率是基波頻率的整數倍。當時稱為二次諧波,時稱為三次諧波等等。是第n次諧波的初相角。
當已知時,傅里葉級數表達式中各諧波分量的系數可由下面公式求得:
???????? (6-1-4)
下面用一個具體例子來進行傅里葉分解。
例6-1-1?? 圖6-1-1所示為對稱方波電壓,其表達式可寫為:
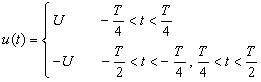
求此信號的傅里葉級數展開式。

圖 6-1-1
解:根據傅里葉級數的系數推導公式,可得
![]()
![]()
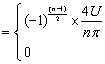
?
![]()
?
由此可得所求信號的傅里葉級數展開式為
![]()
在實際工程計算中,由于傅里葉級數展開為無窮級數,因此要根據級數展開后的收斂情況,電路頻率特性及精度要求,來確定所取的項數。一般只要取前面幾項主要諧波分量即可。例如對于上述方波展開的傅里葉級數表達式,當取不同項數合成時,其合成波形畫于圖6-1-2中。由圖可見,當取諧波項數越多時,合成波形就越接近于原來的理想方波,與原波形偏差越小。

圖 6-1-2
在對一些非正弦周期信號展開時,可根據函數的對稱性質來確定展開式中的系數變化情況。如果函數為偶函數,![]() ,波形對稱于Y軸(見圖6-1-3a),此時它的傅里葉級數展開式中不存在
,波形對稱于Y軸(見圖6-1-3a),此時它的傅里葉級數展開式中不存在![]() 項諧波,即有
項諧波,即有![]() ,此項不必計算。如果函數為奇函數,即有
,此項不必計算。如果函數為奇函數,即有![]() ,波形對稱于原點(見圖6-1-3b),它的傅里葉級數中不包含
,波形對稱于原點(見圖6-1-3b),它的傅里葉級數中不包含![]() 項諧波與直流分量,即有
項諧波與直流分量,即有![]() ,
,![]() 。如果函數滿足
。如果函數滿足![]() ,即將波形移動半個周期后與原波形對稱于X軸(見圖6-1-3c),則其傅里葉級數展開后不包含偶次諧波分量,即有
,即將波形移動半個周期后與原波形對稱于X軸(見圖6-1-3c),則其傅里葉級數展開后不包含偶次諧波分量,即有![]() 。關于傅里葉級數的詳細討論可參見有關書籍。
。關于傅里葉級數的詳細討論可參見有關書籍。
?

圖 6-1-3
非正弦周期信號除了可以表示成上述三角函數形式的傅里葉級數展開式外,還可表示成指數形式的傅里葉級數形式。已知函數可展開成傅里葉級數
![]()
利用歐拉公式
![]()

可得:


因為![]() 對于變量n為奇函數,故有:
對于變量n為奇函數,故有:

同時當![]() 時
時![]() ,因此可以把表達式中的各項統一表達為:
,因此可以把表達式中的各項統一表達為:
![]() ??????? (6-1-5)
??????? (6-1-5)
上式就是傅里葉級數復指數形式的表達式,它把一個周期信號表示成一系列以![]() 為指數的復指數函數式,式中:
為指數的復指數函數式,式中:
![]() ?????????????? (6-1-6)
?????????????? (6-1-6)
系數an、bn與傅里葉三角展開式中的系數一致。![]() 可由下式直接求出:
可由下式直接求出:
![]()
![]()
或 ???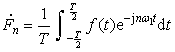 ???????????(6-1-8)
???????????(6-1-8)
![]() 為
為![]() 函數,它代表了信號中各諧波分量的所有信息。
函數,它代表了信號中各諧波分量的所有信息。![]() 的模為對應諧波分量的幅值的一半,而
的模為對應諧波分量的幅值的一半,而![]() 的幅角(當n取正值時)則為對應諧波分量的初相角。它是一個已知信號的頻域表達式,與信號的時域表達式是完全等價的。
的幅角(當n取正值時)則為對應諧波分量的初相角。它是一個已知信號的頻域表達式,與信號的時域表達式是完全等價的。![]() 稱為給定信號的頻譜函數。
稱為給定信號的頻譜函數。![]() 幅值隨
幅值隨![]() 變化的關系
變化的關系![]() 稱為振幅頻譜,
稱為振幅頻譜,![]() 的相位隨
的相位隨![]() 變化的關系
變化的關系![]() 稱為相位頻譜。由于系數
稱為相位頻譜。由于系數![]() ,
,![]() ,因此振幅頻譜為偶函數,而相位頻譜則為奇函數。信號所包含的各諧波幅值與相位可用幅頻特性和相頻特性圖來直觀表示。
,因此振幅頻譜為偶函數,而相位頻譜則為奇函數。信號所包含的各諧波幅值與相位可用幅頻特性和相頻特性圖來直觀表示。
例6-1-2?? 周期脈沖信號如圖6-1-4a所示,求該信號的頻譜函數![]() ,并作振幅頻譜和相位頻譜圖。
,并作振幅頻譜和相位頻譜圖。
解:由波形圖可知:

頻譜函數為:

?????????????????????????????????????????????????????  ??????????????(6-1-9)
??????????????(6-1-9)
若![]() ,則可得:
,則可得:

由上式可作出振幅頻譜與相位頻譜圖,如圖6-1-4b、c所示。
?
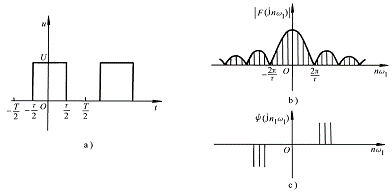
圖 6-1-4
從振幅頻譜圖可看出,周期信號的頻譜圖是一系列離散的譜線組成的,所有譜線都出現在基波頻率的整數倍的頻率上。周期信號的這種頻譜稱為離散頻譜。
從頻譜函數表達式中可看出,當脈沖重復周期增大時,基波頻率![]() 將變小,譜線之間的間隔縮小,同時振幅也隨之減小。當T無限增大時,譜線將趨于無限密集,即從離散趨于連續,而幅值卻趨于無窮小,這時周期信號也已轉化為非周期信號。
將變小,譜線之間的間隔縮小,同時振幅也隨之減小。當T無限增大時,譜線將趨于無限密集,即從離散趨于連續,而幅值卻趨于無窮小,這時周期信號也已轉化為非周期信號。
 電子發燒友App
電子發燒友App








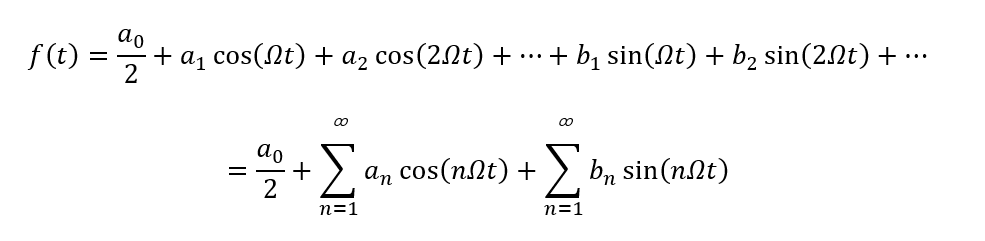






























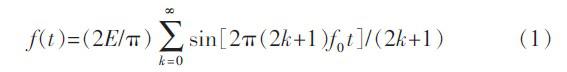











評論