定點補碼一位除法的實現方案
與補碼乘法類似,也可以用補碼直接完成除法運算,即用 [X]補/[Y] 補 直接求得[X/Y]補 。補碼除法的規則比原碼除法的規則復雜一些。當除數和被除數用補表示時,判別是否夠除,就不再是簡單地用被除數(余數)減去除數,而是要比較它們的絕對值的大小。因此,若二數同符號,要用減法,若異號,則要用加法,請注意,這樣求出來的商是反碼形式的。
我們不準備對此進行更多地討論,可以給出其運算規則如下:
(1) 開始時,求第一位商,如果被除數與除數同號, 用被除數減去除數,若二數異號,則用被除數加上除數的辦法處理。
(2) 運算過程中確定商的值,若余數與除數同號,上商1,左移一位后下次用余數減除數操作求商,若余數與除數異號,上商0,左移一位后下次用余數加除數操作求商。
(3) 商的符號,是在第一次求商試算時求出的,若定點除不溢出,得到的就是正確的符號位的值。
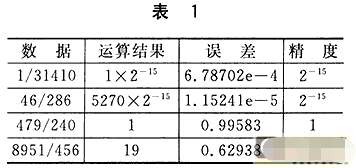
(4) 商的修正問題。在對精度要求不高時,將商的最低一位恒置1。最大誤差為 | 2-n |。
若對商的精度要求較高,可對n位數求商n+1次,按得到的不同結果對商進行修正。當商為負時,要在商的最低一位加1,從反碼的結果得到商的正確的補碼值。
下面給出補碼除法執行運算過程的一個實例。
假定 [X]補 =1 0111 , [Y]補 = 0 1101, 則 [-Y]補 = 1 0011
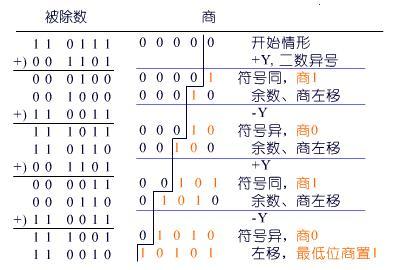
再求下去,可得下一位商并舍入;也可以不執行最后一步求商操作,而直接用在最低位上商1來結束除運算過程。
除法運算也有快速除運算的各種方案,如一次求得1位或多位商的跳0跳1法,專用的高速除法裝置,用快速乘法器完成快速除運算等。由于在程序中,除法指令的使用頻度不高,因此一般機器中較少采用快速除法方案。
與補碼乘法類似,也可以用補碼直接完成除法運算,即用 [X]補/[Y] 補 直接求得[X/Y]補 。補碼除法的規則比原碼除法的規則復雜一些。當除數和被除數用補表示時,判別是否夠除,就不再是簡單地用被除數(余數)減去除數,而是要比較它們的絕對值的大小。因此,若二數同符號,要用減法,若異號,則要用加法,請注意,這樣求出來的商是反碼形式的。
我們不準備對此進行更多地討論,可以給出其運算規則如下:
(1) 開始時,求第一位商,如果被除數與除數同號, 用被除數減去除數,若二數異號,則用被除數加上除數的辦法處理。
(2) 運算過程中確定商的值,若余數與除數同號,上商1,左移一位后下次用余數減除數操作求商,若余數與除數異號,上商0,左移一位后下次用余數加除數操作求商。
(3) 商的符號,是在第一次求商試算時求出的,若定點除不溢出,得到的就是正確的符號位的值。
(4) 商的修正問題。在對精度要求不高時,將商的最低一位恒置1。最大誤差為 | 2-n |。
若對商的精度要求較高,可對n位數求商n+1次,按得到的不同結果對商進行修正。當商為負時,要在商的最低一位加1,從反碼的結果得到商的正確的補碼值。
下面給出補碼除法執行運算過程的一個實例。
假定 [X]補 =1 0111 , [Y]補 = 0 1101, 則 [-Y]補 = 1 0011

再求下去,可得下一位商并舍入;也可以不執行最后一步求商操作,而直接用在最低位上商1來結束除運算過程。
除法運算也有快速除運算的各種方案,如一次求得1位或多位商的跳0跳1法,專用的高速除法裝置,用快速乘法器完成快速除運算等。由于在程序中,除法指令的使用頻度不高,因此一般機器中較少采用快速除法方案。
 電子發燒友App
電子發燒友App













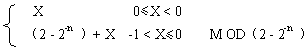










評論