什么是基爾霍夫定律
基爾霍夫定律Kirchhoff laws是電路中電壓和電流所遵循的基本規(guī)律,是分析和計算較為復雜電路的基礎(chǔ),1845年由德國物理學家G.R.基爾霍夫(Gustav Robert Kirchhoff,1824~1887)提出。它既可以用于直流電路的分析,也可以用于交流電路的分析,還可以用于含有電子元件的非線性電路的分析。運用基爾霍夫定律進行電路分析時,僅與電路的連接方式有關(guān),而與構(gòu)成該電路的元器件具有什么樣的性質(zhì)無關(guān)。基爾霍夫定律包括電流定律和電壓定律。
基本概念
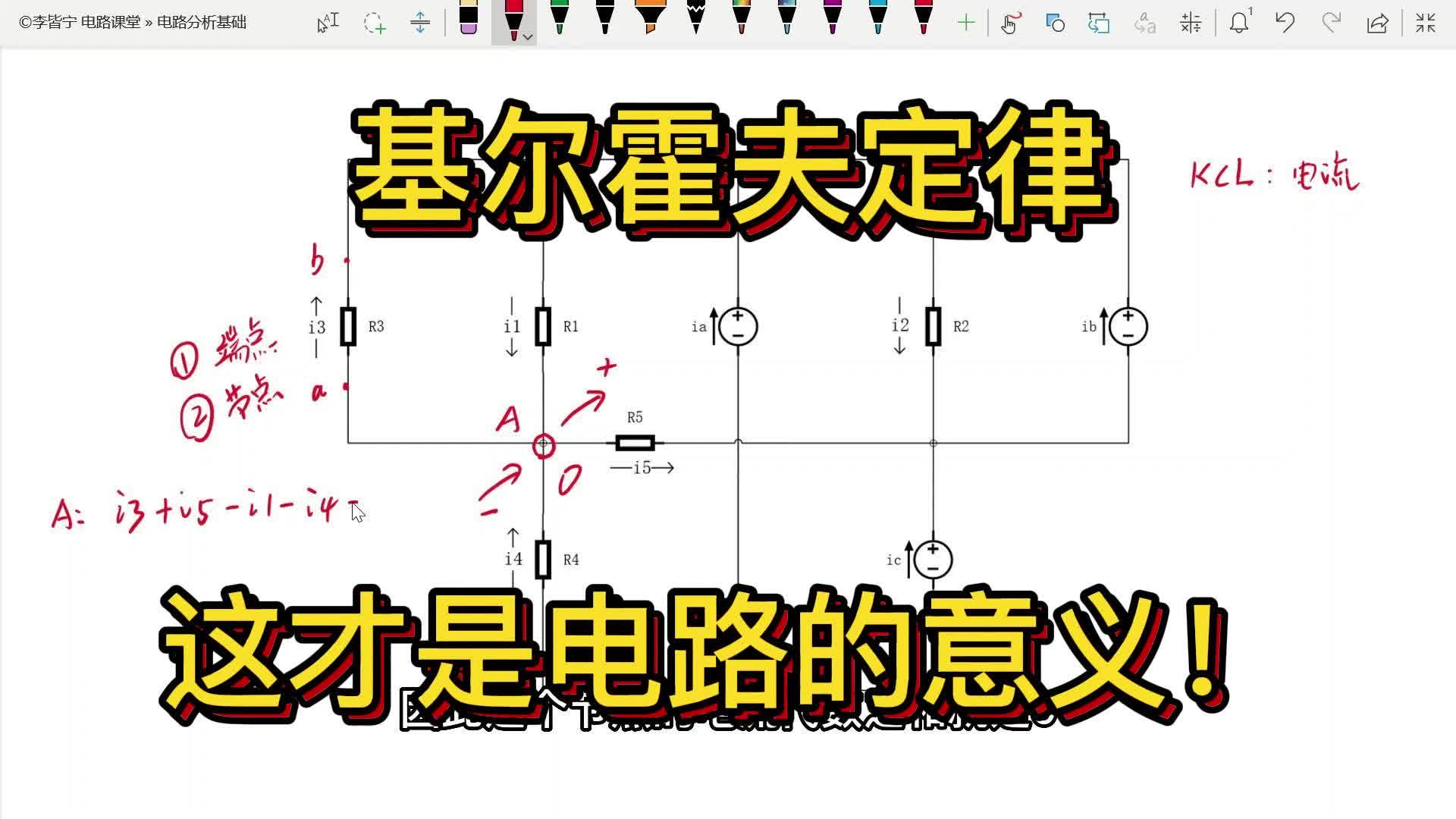
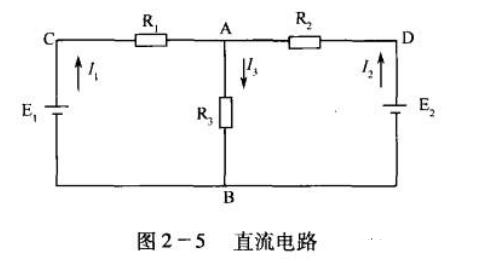
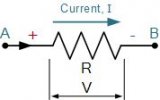
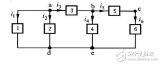
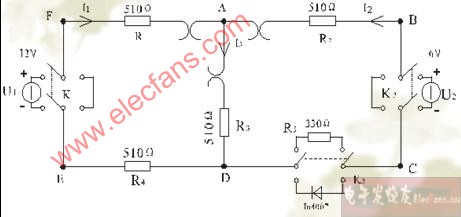
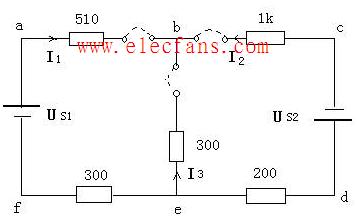
⑴ 支路:由一個或幾個元件首尾相接組成的無分支電路。圖

中共有5條支路,支路電流分別標于圖中。
⑵ 節(jié)點:三條或三條以上支路的連接點。圖中共有a、b、c三個節(jié)點。
⑶ 回路:電路中任何一個閉合路徑。圖中共有6個回路。
⑷網(wǎng)孔:中間無任何支路穿過的回路。網(wǎng)孔是最簡單的回路,或是不可再分的回路。,圖中最簡單的回路aR1R2a,aR2R4ba,bR4R5b三個是網(wǎng)孔。
基爾霍夫第一定律
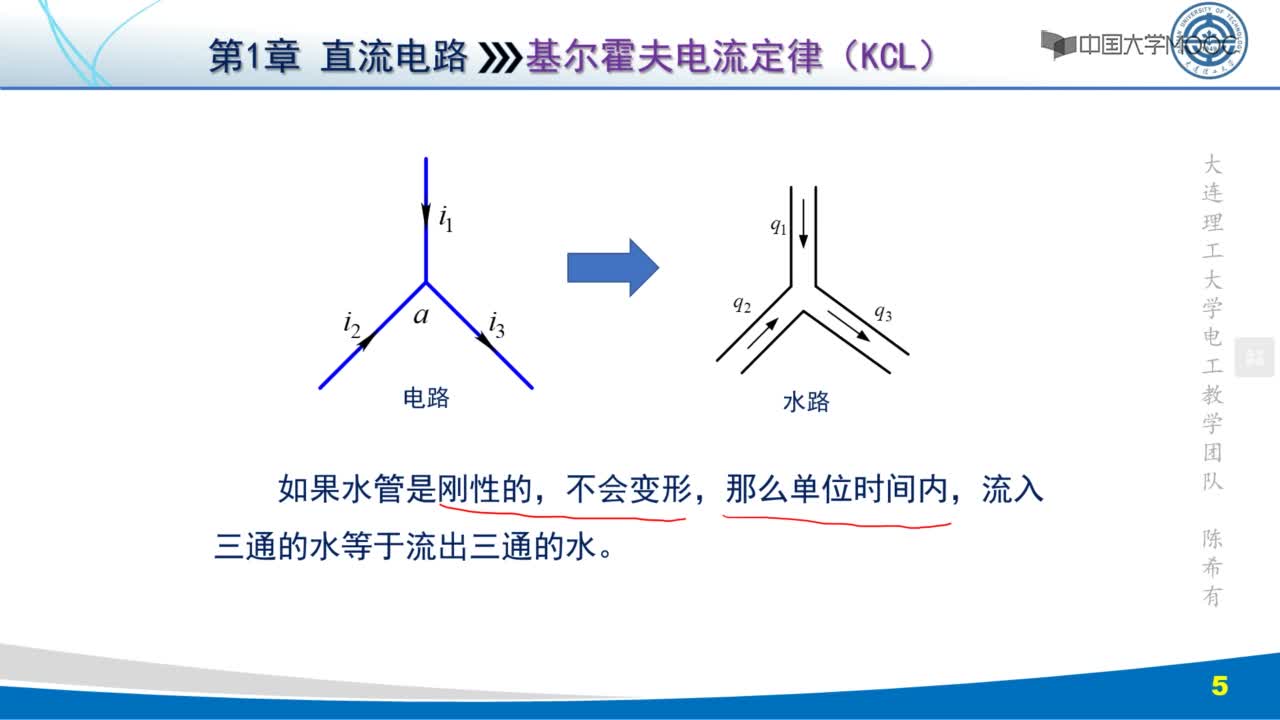
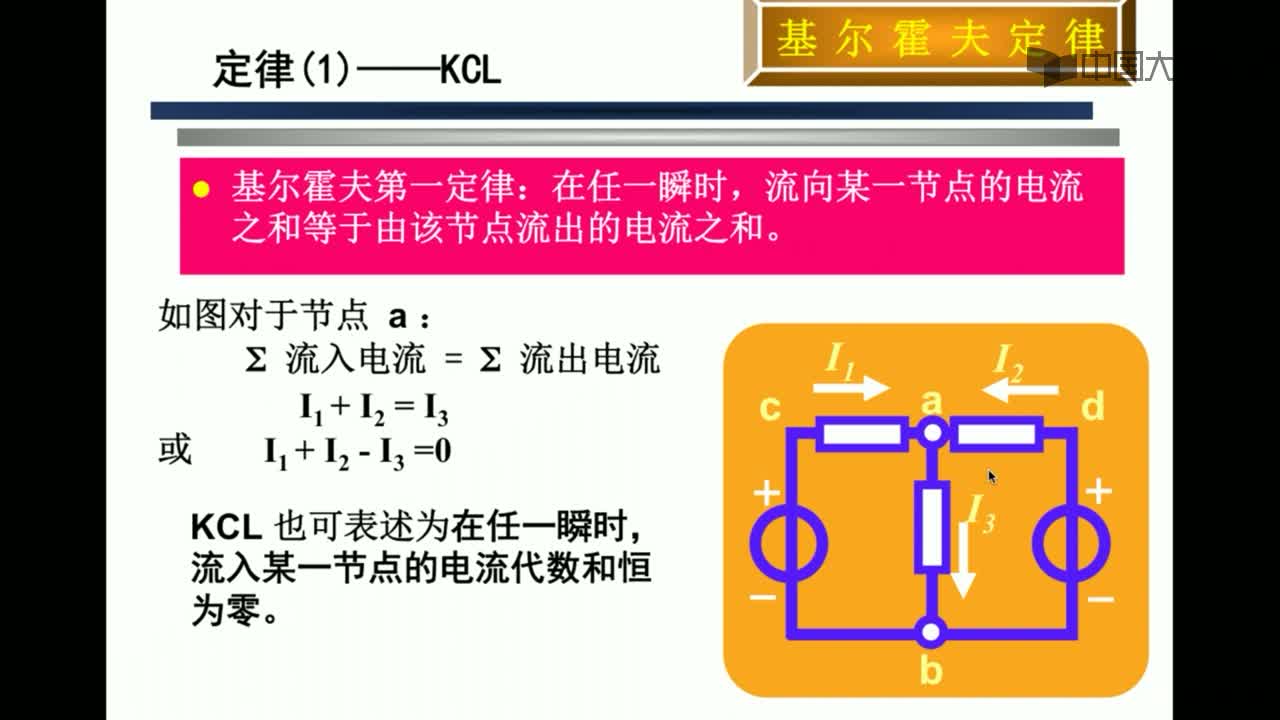
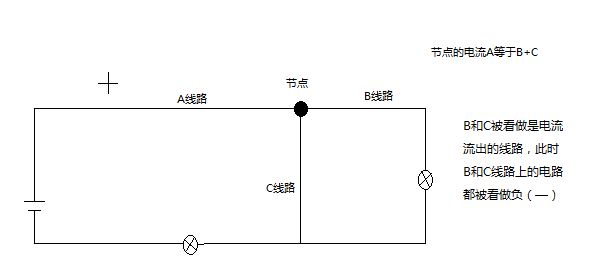
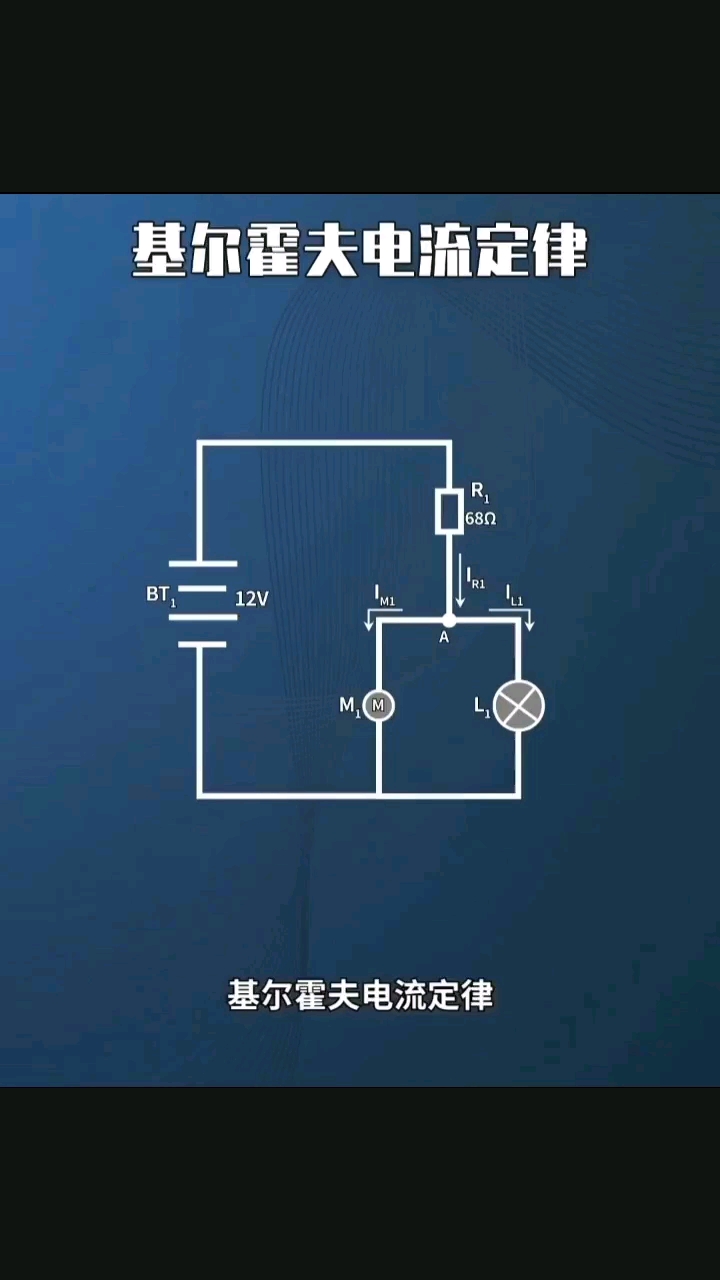
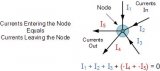
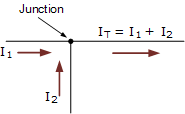
⑴ 內(nèi)容:在任一瞬間,對電路中的任一節(jié)點,流進某一節(jié)點的電流之和恒等于
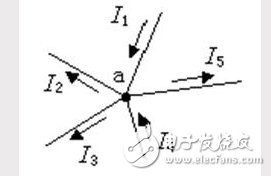
流出該節(jié)點的電流之和。
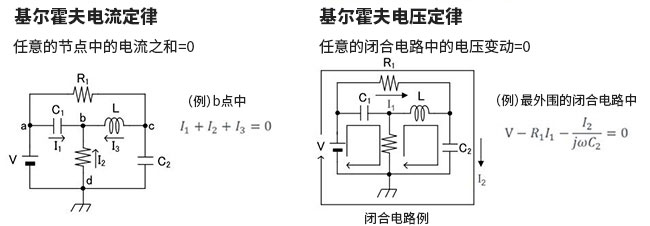
⑵ 公式:∑I入=∑I出
⑶ 定律討論的對象:節(jié)點電流(故基爾霍夫第一定律又稱為節(jié)點電流定律)。
I1+I3+I2+I4+I5=0,即:∑I=0
上式表明:若規(guī)定流入節(jié)點的電流以為“+I”,流出節(jié)點的電流為“-I”,則節(jié)點電流定律又可敘述為:在任一瞬間通過電路中任一節(jié)點,流入(或流出)該節(jié)點電流的代數(shù)和恒等于零。
基爾霍夫第二定律(回路電壓定律)
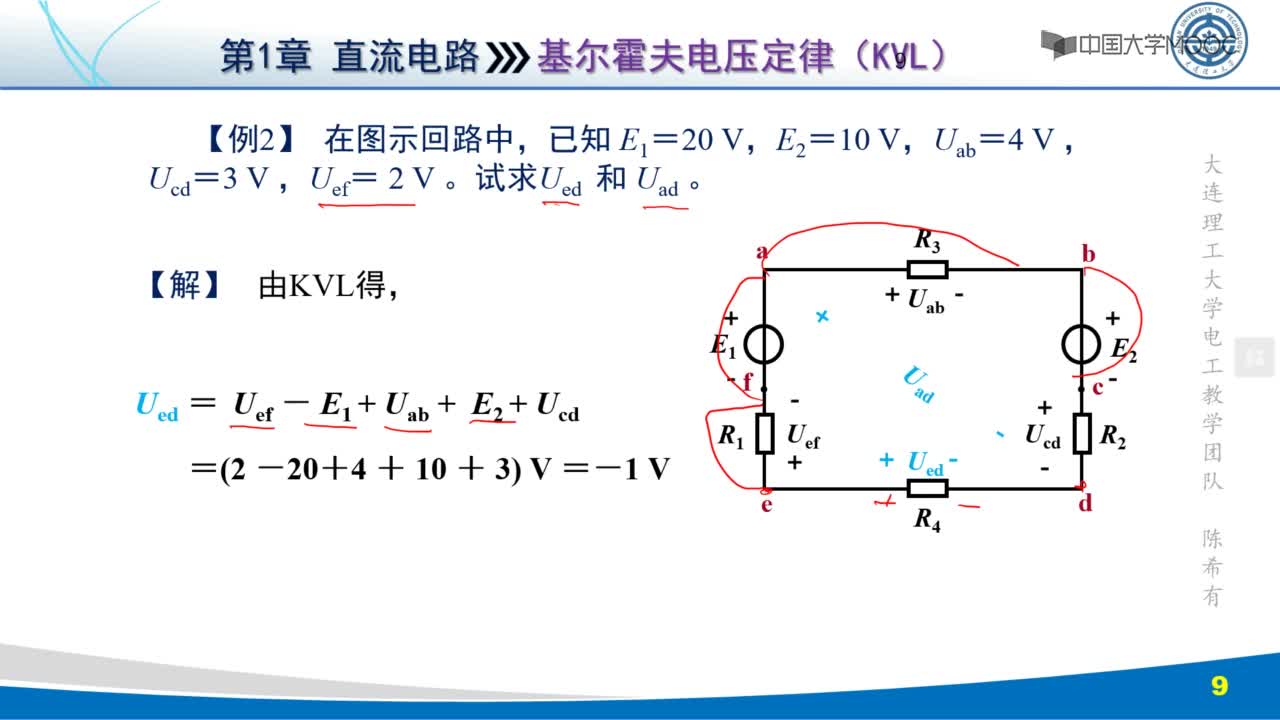
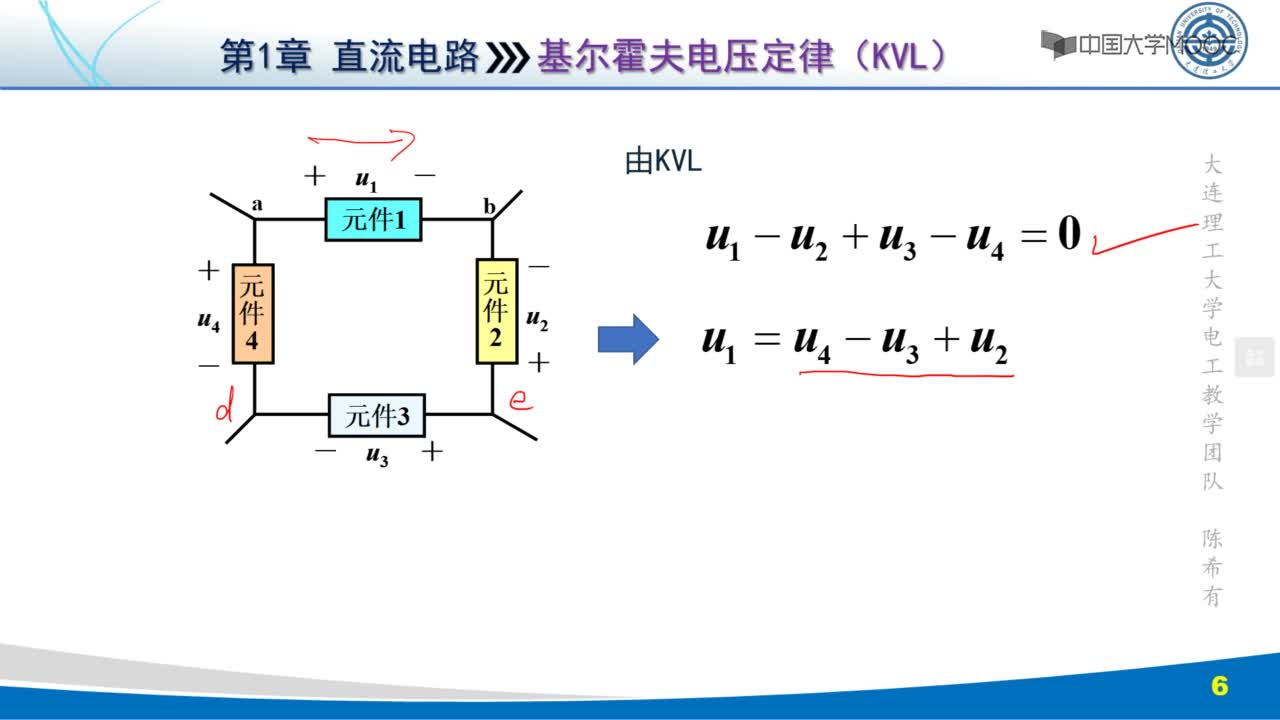
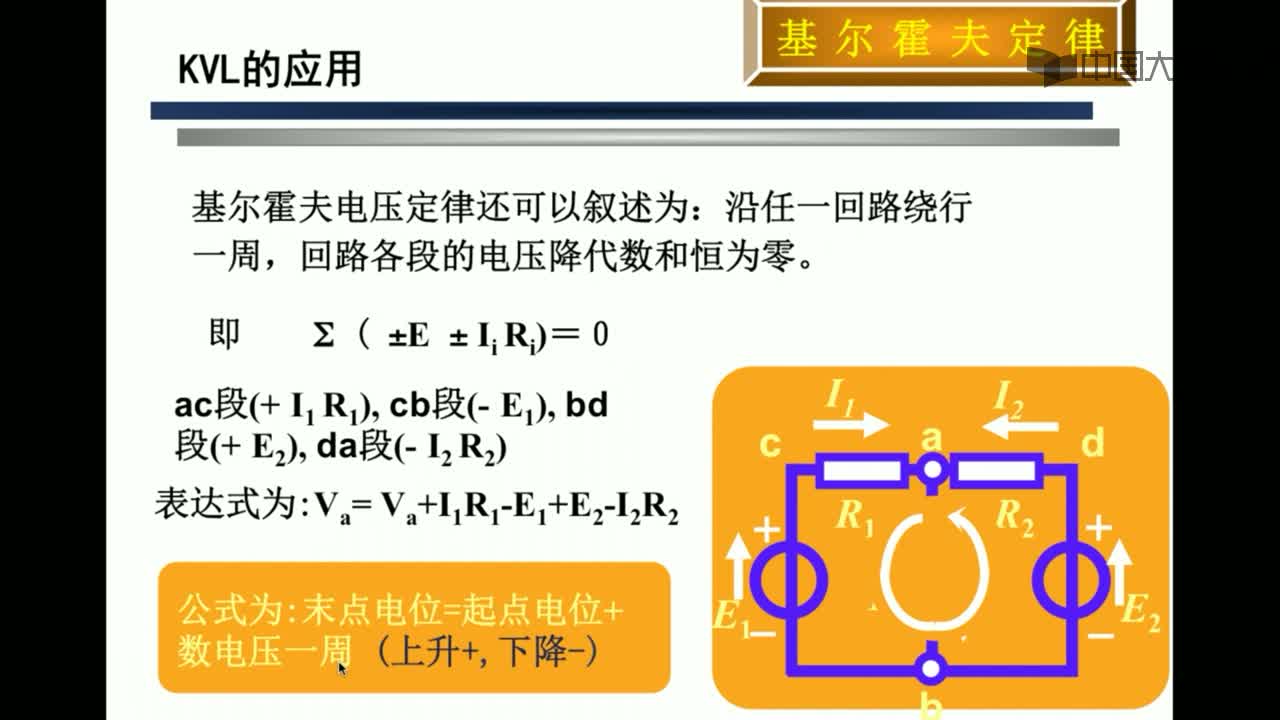
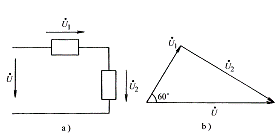
⑴內(nèi)容:在任一瞬間,對任一閉合回路,沿回路繞行方向上各段

電壓代數(shù)和恒等于零。
⑵公式:∑U=0
⑶定律討論的對象:回路上的電壓(故基爾霍夫第二定律又稱為回路電壓定律)。
對于電路中的任意一個回路(此回路斷開與否均可)。有:電動勢的代數(shù)和等于電壓降的代數(shù)和。其數(shù)學表達式為:∑E=∑IR=∑U電動勢和電壓降的正負由方向確定,即電動勢和電壓降的正方向與回路的循行方向一致時取正,反之取負。
上式表明:在任一回路循環(huán)方向中,回路中各電動勢的代數(shù)和恒等于各電阻上電壓降的代數(shù)和。
基爾霍夫定律的應用
基爾霍夫電流定律(KCL)描述了電路中各支路的電流之間的關(guān)系,
基爾霍夫電壓定律(KVL)描述了電路中各支路電壓之間的關(guān)系,它們都與電路元件的性質(zhì)無關(guān),而只取決于電路的連接方式。所以我們把這種約束關(guān)系稱為連接方式約束或拓撲約束,而把根據(jù)它們寫出來的方程分別稱為KCL約束方程和KVL約束方程。

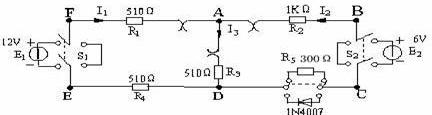
基爾霍夫第一定律的推廣:節(jié)點電流不僅適用于節(jié)點,還可推廣于任意假設(shè)的封閉面來說,它仍然成立。下圖電路中閉合面所包圍的是一個三角形電路,有三個節(jié)點。
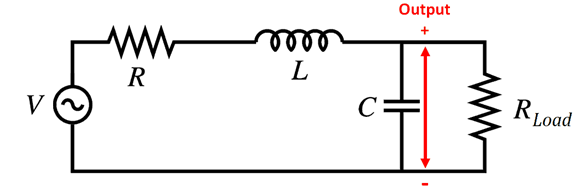
基爾霍夫第二定律的推廣:可以推廣到用于不完全由實際元件構(gòu)成的假想回路,如圖所示。
 電子發(fā)燒友App
電子發(fā)燒友App


























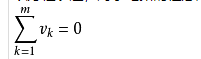
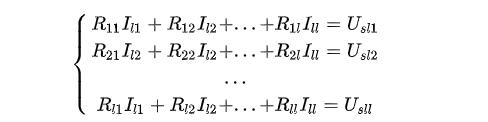
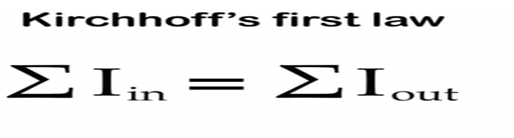
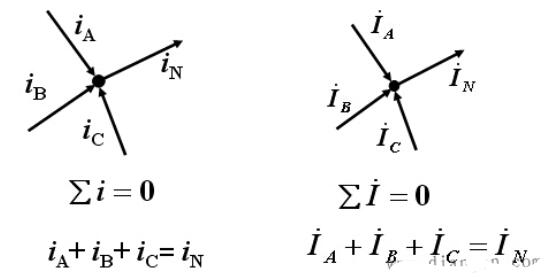


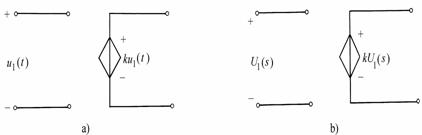











評論