將物理或抽象對象的集合分成由類似的對象組成的多個類的過程被稱為聚類。由聚類所生成的簇是一組數據對象的集合，這些對象與同一個簇中的對象彼此相似，與其他簇中的對象相異。

　　（一）原理部分

　　模糊C均值（Fuzzy C-means）算法簡稱FCM算法，是一種基于目標函數的模糊聚類算法，主要用于數據的聚類分析。理論成熟，應用廣泛，是一種優秀的聚類算法。本文關于FCM算法的一些原理推導部分介紹等參考下面視頻，加上自己的理解以文字的形式呈現出來，視頻參考如下，比較長，看不懂的可以再去看看：

　　FCM原理介紹

　　FCM分析1

　　FCM分析2

　　FCM分析3

　　首先介紹一下模糊這個概念，所謂模糊就是不確定，確定性的東西是什么那就是什么，而不確定性的東西就說很像什么。比如說把20歲作為年輕不年輕的標準，那么一個人21歲按照確定性的劃分就屬于不年輕，而我們印象中的觀念是21歲也很年輕，這個時候可以模糊一下，認為21歲有0.9分像年輕，有0.1分像不年輕，這里0.9與0.1不是概率，而是一種相似的程度，把這種一個樣本屬于結果的這種相似的程度稱為樣本的隸屬度，一般用u表示，表示一個樣本相似于不同結果的一個程度指標。

　　基于此，假定數據集為X，如果把這些數據劃分成c類的話，那么對應的就有c個類中心為C，每個樣本j屬于某一類i的隸屬度為uij，那么定義一個FCM目標函數（1）及其約束條件（2）如下所示：

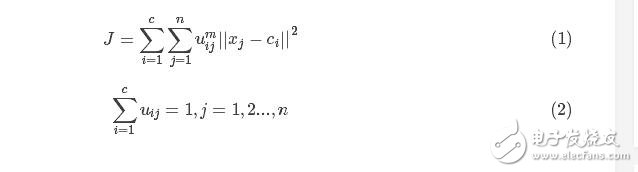
　　看一下目標函數（式1）而知，由相應樣本的隸屬度與該樣本到各個類中心的距離相乘組成的，m是一個隸屬度的因子，個人理解為屬于樣本的輕緩程度，就像x2與x3這種一樣。式（2）為約束條件，也就是一個樣本屬于所有類的隸屬度之和要為1。觀察式（1）可以發現，其中的變量有uij、ci，并且還有約束條件，那么如何求這個目標函數的極值呢？

　　這里首先采用拉格朗日乘數法將約束條件拿到目標函數中去，前面加上系數，并把式（2）的所有j展開，那么式（1）變成下列所示：

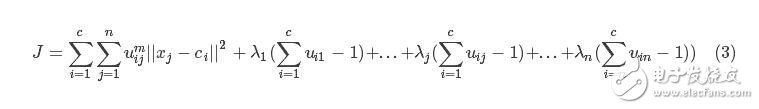
　　現在要求該式的目標函數極值，那么分別對其中的變量uij、ci求導數，首先對uij求導。

　　分析式（3），先對第一部分的兩級求和的uij求導，對求和形式下如果直接求導不熟悉，可以把求和展開如下：

　　再來看后面那個對uij求導，同樣把求和展開，再去除和uij不相關的（求導為0），那么只剩下這一項：λj（uij?1），它對uij求導就是λj了。

　　那么最終J對uij的求導結果并讓其等于0就是：

　　我們發現uij與ci是相互關聯的，彼此包含對方，有一個問題就是在fcm算法開始的時候既沒有uij也沒有ci，那要怎么求解呢？很簡單，程序開始的時候我們隨便賦值給uij或者ci其中的一個，只要數值滿足條件即可。然后就開始迭代，比如一般的都賦值給uij，那么有了uij就可以計算ci，然后有了ci又可以計算uij，反反復復，在這個過程中還有一個目標函數J一直在變化，逐漸趨向穩定值。那么當J不在變化的時候就認為算法收斂到一個比較好的結了。可以看到uij和ci在目標函數J下似乎構成了一個正反饋一樣，這一點很像EM算法，先E在M，有了M在E，在M直至達到最優。

　　公式（5），（6）是算法的關鍵。現在來重新從宏觀的角度來整體看看這兩個公式，先看（5），在寫一遍

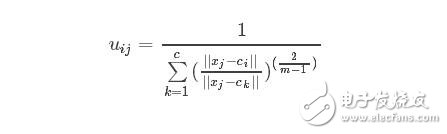
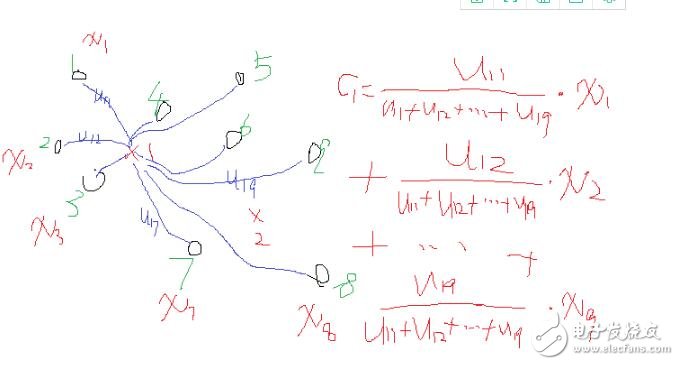
　　假設看樣本集中的樣本1到各個類中心的隸屬度，那么此時j=1，i從1到c類，此時上述式中分母里面求和中，分子就是這個點相對于某一類的類中心距離，而分母是這個點相對于所有類的類中心的距離求和，那么它們兩相除表示什么，是不是表示這個點到某個類中心在這個點到所有類中心的距離和的比重。當求和里面的分子越小，是不是說就越接近于這個類，那么整體這個分數就越大，也就是對應的uij就越大，表示越屬于這個類，形象的圖如下：

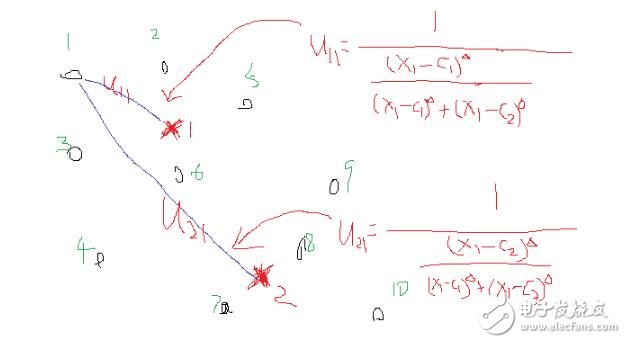
　　再來宏觀看看公式（6），考慮當類i確定后，式（6）的分母求和其實是一個常數，那么式（6）可以寫成：

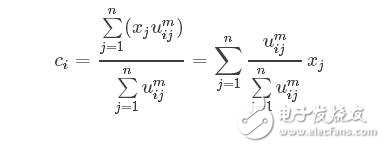
　　這是類中心的更新法則。說這之前，首先讓我們想想kmeans的類中心是怎么更新的，一般最簡單的就是找到屬于某一類的所有樣本點，然后這一類的類中心就是這些樣本點的平均值。那么FCM類中心怎么樣了？看式子可以發現也是一個加權平均，類i確定后，首先將所有點到該類的隸屬度u求和，然后對每個點，隸屬度除以這個和就是所占的比重，乘以xj就是這個點對于這個類i的貢獻值了。畫個形象的圖如下：

　　由上述的宏觀分析可知，這兩個公式的迭代關系式是這樣的也是可以理解的。

　　（二）簡單程序實現

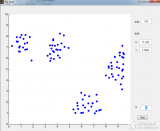
　　下面我們在matlab下用最基礎的循環實現上述的式（5）與式（6）的FCM過程。首先，我們需要產生可用于FCM的數據，為了可視化方便，我們產生一個二維數據便于在坐標軸上顯示，也就是每個樣本由兩個特征（或者x坐標與y坐標構成），生成100個這樣的點，當然我們在人為改變一下，讓這些點看起來至少屬于不同的類。生成的點畫出來如下：

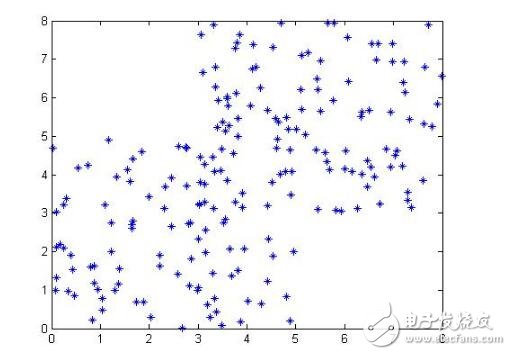
　　那么我們說FCM算法的一般步驟為：

　　（1）確定分類數，指數m的值，確定迭代次數（這是結束的條件，當然結束的條件可以有多種）。

　　（2）初始化一個隸屬度U（注意條件—和為1）；

　　（3）根據U計算聚類中心C；

　　（4）這個時候可以計算目標函數J了

　　（5）根據C返回去計算U，回到步驟3，一直循環直到結束。

　　還需要說一點的是，當程序結束后，怎么去判斷哪個點屬于哪個類呢？在結束后，肯定有最后一次計算的U吧，對于每一個點，它屬于各個類都會有一個u，那么找到其中的最大的u就認為這個點就屬于這一類。基于此一個基礎的程序如下：

　　clc

　　clear

　　close all

　　%% create samples：

　　for i=1:100

　　x1（i） = rand（）*5; %人為保證差異性

　　y1（i） = rand（）*5;

　　x2（i） = rand（）*5 + 3; %人為保證差異性

　　y2（i） = rand（）*5 + 3;

　　end

　　x = ［x1，x2］;

　　y = ［y1，y2］;

　　data = ［x;y］;

　　data = data‘;%一般數據每一行代表一個樣本

　　%plot（data（：，1），data（：，2），’*‘）; %畫出來

　　%%---

　　cluster_n = 2;%類別數

　　iter = 50;%迭代次數

　　m = 2;%指數

　　num_data = size（data，1）;%樣本個數

　　num_d = size（data，2）;%樣本維度

　　%--初始化隸屬度u，條件是每一列和為1

　　U = rand（cluster_n，num_data）;

　　col_sum = sum（U）;

　　U = U./col_sum（ones（cluster_n，1），：）;

　　%% 循環--規定迭代次數作為結束條件

　　for i = 1:iter

　　%更新c

　　for j = 1:cluster_n

　　u_ij_m = U（j，：）.^m;

　　sum_u_ij = sum（u_ij_m）;

　　sum_1d = u_ij_m./sum_u_ij;

　　c（j，：） = u_ij_m*data./sum_u_ij;

　　end

　　%-計算目標函數J

　　temp1 = zeros（cluster_n，num_data）;

　　for j = 1:cluster_n

　　for k = 1:num_data

　　temp1（j，k） = U（j，k）^m*（norm（data（k，：）-c（j，：）））^2;

　　end

　　end

　　J（i） = sum（sum（temp1））;

　　%更新U

　　for j = 1:cluster_n

　　for k = 1:num_data

　　sum1 = 0;

　　for j1 = 1:cluster_n

　　temp = （norm（data（k，：）-c（j，：））/norm（data（k，：）-c（j1，：）））.^（2/（m-1））;

　　sum1 = sum1 + temp;

　　end

　　U（j，k） = 1./sum1;

　　end

　　end

　　end

　　figure;

　　subplot（1，2，1），plot（J）;

　　［~，label］ = max（U）; %找到所屬的類

　　subplot（1，2，2）;

　　gscatter（data（：，1），data（：，2），label）123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960

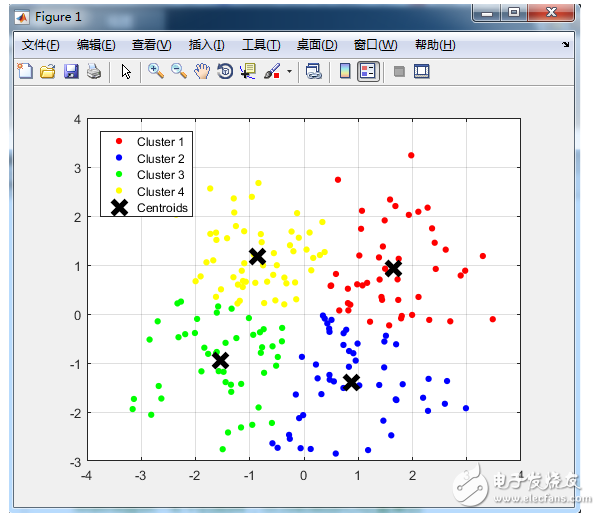
　　得到結果如下：

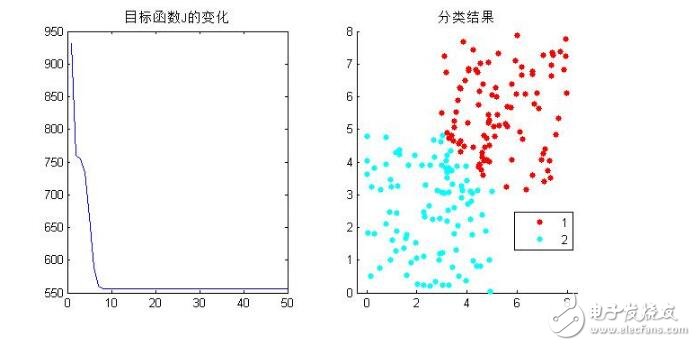
　　分成3類看看：

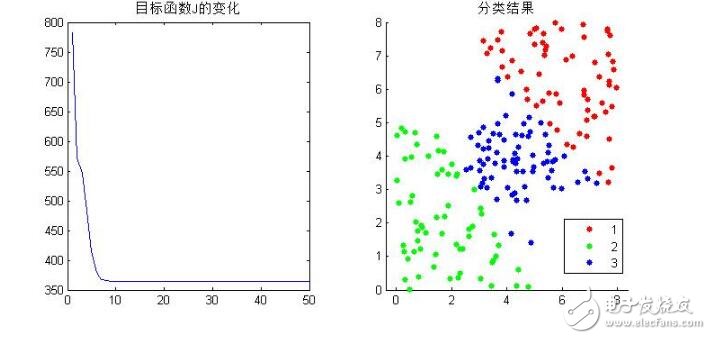
　　基于此，結果還算正確。但是不得不說的一個問題就是算法的效率問題。為了和公式計算方式吻合，便于理解，這個程序里面有很多的循環操作，當分類數大一點，樣本多一點的時候，這么寫是很慢的，matlab號稱矩陣實驗室，所以要盡量少的使用循環，直接矩陣操作，那么上述的操作很多地方是可以把循環改成矩陣計算的，這里來介紹下matlab自帶的fcm函數，就是使用矩陣運算來的。

　　Matlab下help fcm既可以查閱相關用法們這里只是簡單介紹，fcm函數輸入需要2個或者3個參數，返回3個參數，如下：

　　［center， U， obj_fcn］ = fcm（data， cluster_n， options）

　　對于輸入：data數據集（注意每一行代表一個樣本，列是樣本個數）

　　cluster_n為聚類數。

　　options是可選參數，完整的options包括：

　　OPTIONS（1）： U的指數 （default： 2.0）

　　OPTIONS（2）： 最大迭代次數 （default： 100）

　　OPTIONS（3）： 目標函數的最小誤差 （default： 1e-5）

　　OPTIONS（4）： 是否顯示結果 （default： 1，顯示）

　　options都有默認值，自帶的fcm結束的條件是OPTIONS（2）與OPTIONS（3）有一個滿足就結束。

　　對于輸出：center聚類中心，U隸屬度，obj_fcn目標函數值，這個迭代過程的每一代的J都在這里面存著。

　　為了驗證我們寫的算法是否正確，用它的fcm去試試我們的數據（前提是數據一樣），分成3類，畫出它們的obj_fcn看看如下：

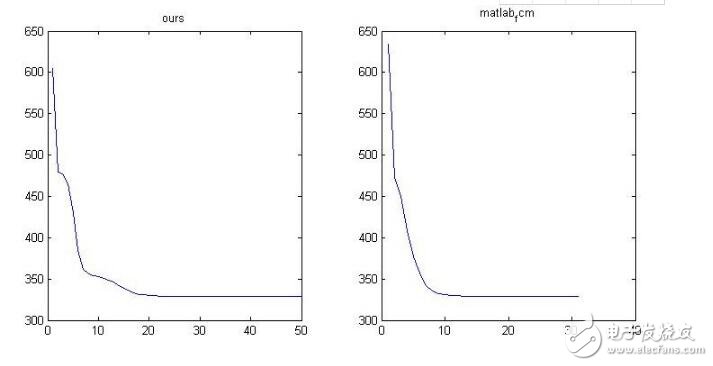
　　可以看到，雖然迭代的中間過程不一樣，但是結果卻是一樣的。

　　（三）進階應用

　　了解了fcm，再來看看它的幾個應用。

　　3.1）基于fcm的圖像分割

　　我們知道fcm主要用于聚類，而圖像分割本身就是一個聚類的過程。所以可以用fcm去實現圖像分割。

　　這里以matlab下的灰度圖像為例。灰度圖像一圖像的角度看是二維的，但是我們知道，決定圖像的無非是里面的灰度值。而灰度值就是一個值，所以當我們把圖像變成1維，也就是拉成一行或者一列的時候，其實灰度圖像就是一個一維數據（上面那個例子生成的隨機點是二維的）。

　　那么我們就可以對這個一維數據進行聚類，待得到了分類結果后，再把這個結果返回到二維圖像空間去顯示就可以了。

　　一個例子如下：

　　clc

　　clear

　　close all

　　img = double（imread（’lena.jpg‘））;

　　subplot（1，2，1），imshow（img，［］）;

　　data = img（：）;

　　%分成4類

　　［center，U，obj_fcn］ = fcm（data，4）;

　　［~，label］ = max（U）; %找到所屬的類

　　%變化到圖像的大小

　　img_new = reshape（label，size（img））;

　　subplot（1，2，2），imshow（img_new，［］）;123456789101112

　　需要注意的是label出來的是標簽類別（1-4），并非真實的灰度，這里不過是把它顯示出來就行了。

　　3.2）實際數據的分類

　　這里介紹一個常用于機器學習、模式劃分的數據下載網站：

　　http://archive.ics.uci.edu/ml/datasets.html

　　這里面包含眾多的數據庫可用分類劃分等。這里我們選擇其中一個數據庫：

　　http://archive.ics.uci.edu/ml/datasets/seeds#

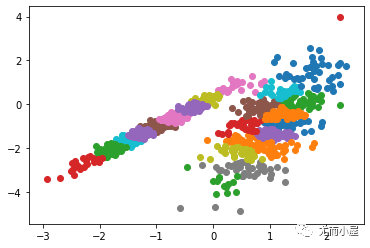
　　這個數據庫看介紹好像是關于種子分類的，里面共包含3類種子，每類種子通過什么x射線技術等等采集他們的特征，反正最后每個種子共有7個特征值來表示它（也就是說在數據里面相當于7維），每類種子又有70個樣本，那么整個數據集就是210*7的樣本集。從上面那個地方下載完樣本集存為txt文件，并放到matlab工作目錄下就可以使用了（注意看看下下來的數據有沒有串位的，有的話要手動調整回去）。因為matlab只能顯示低于3維的數據，這里有7維，我們現在在二維下顯示其中的兩維以及正確的分類結果看看什么情況：

　　clc

　　clear

　　close all

　　data = importdata（’data.txt‘）;

　　%data中還有第8列，正確的標簽列

　　subplot（2，2，1）;

　　gscatter（data（：，1），data（：，6），data（：，8）），title（’choose:1，6 列‘）

　　subplot（2，2，2）;

　　gscatter（data（：，2），data（：，4），data（：，8）），title（’choose:2，4 列‘）

　　subplot（2，2，3）;

　　gscatter（data（：，3），data（：，5），data（：，8）），title（’choose:3，5 列‘）

　　subplot（2，2，4）;

　　gscatter（data（：，4），data（：，7），data（：，8）），title（’choose:4，7 列‘）12345678910111213

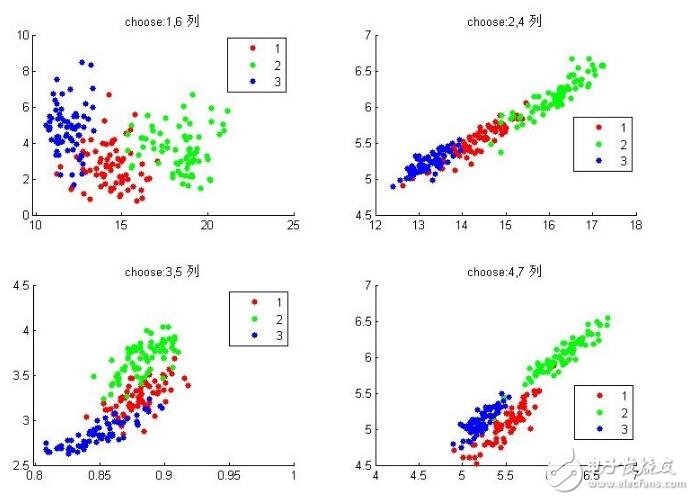
　　組合有限，隨便組合幾種看看，發現似乎任意兩個特征都可以把他們分開，當然還是有一些分不開的，其中最后一個選擇特征4，7似乎很好的分開了。

　　Ok，看過之后我們來試試fcm算法對其進行分類，并計算一下準確率，我們先把7個特征都用上看看：

　　clc

　　clear

　　close all

　　data = importdata（’data.txt‘）;

　　%data中還有第8列，正確的標簽列

　　［center，U，obj_fcn］ = fcm（data（：，1:7），3）;

　　［~，label］ = max（U）; %找到所屬的類

　　subplot（1，2，1）;

　　gscatter（data（：，4），data（：，7），data（：，8）），title（’choose:4，7列，理論結果‘）

　　% cal accuracy

　　a_1 = size（find（label（1:70）==1），2）;

　　a_2 = size（find（label（1:70）==2），2）;

　　a_3 = size（find（label（1:70）==3），2）;

　　a = max（［a_1，a_2，a_3］）;

　　b_1 = size（find（label（71:140）==1），2）;

　　b_2 = size（find（label（71:140）==2），2）;

　　b_3 = size（find（label（71:140）==3），2）;

　　b = max（［b_1，b_2，b_3］）;

　　c_1 = size（find（label（141:210）==1），2）;

　　c_2 = size（find（label（141:210）==2），2）;

　　c_3 = size（find（label（141:210）==3），2）;

　　c = max（［c_1，c_2，c_3］）;

　　accuracy = （a+b+c）/210;

　　% plot answer

　　subplot（1，2，2）;

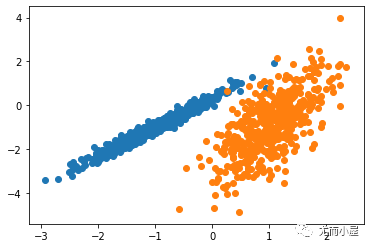
　　gscatter（data（：，4），data（：，7），label），title（［’實際結果，accuracy=‘，num2str（accuracy）］）1234567891011121314151617181920212223242526

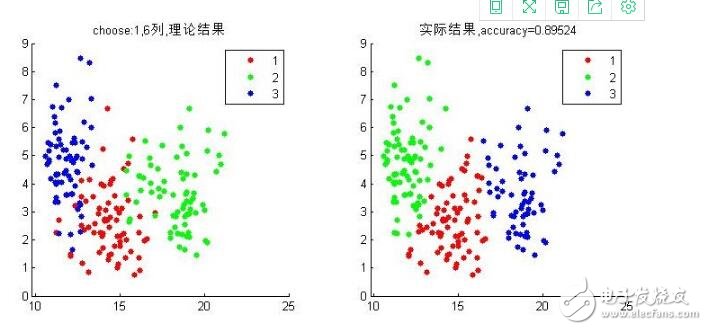
　　這里選擇以第1與6維的數據來可視化這個結果。可以看到準確率為0.89524。

　　這就是用了所有特征來實驗的，這與用哪個特征能到達更好的結果、怎么樣吧特征進行處理下能達到更好的結果，這都是機器學習與分類領域在研究的事情。上面我們感覺特征4，7不錯，那么當我們只用特征4與7去進行fcm會怎樣呢？

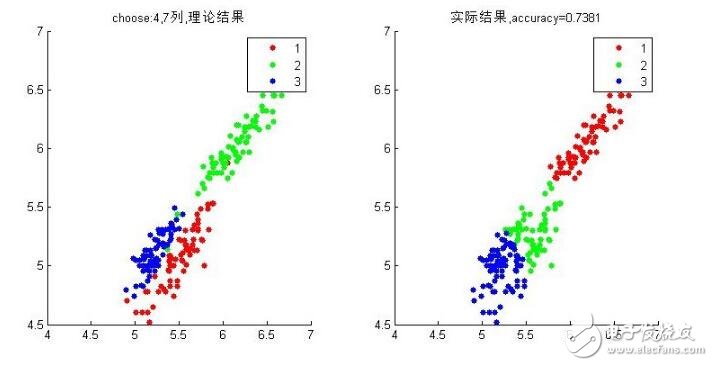
　　好像并不是很好，想想只用特征4與7結果本來就是這樣的，不好就對了，fcm是根據數據距離劃分來的，所以結果就是這樣。

　　試了很多組特征，都沒有超過0.89524的，那就所有特征都用上吧。其實這個準確率是可以提高的，我們看到這7個特征似乎有點重復有沒有，如果我們把這7個特征采用pca降維到3，4個特征了再去fcm實驗呢？可以去試試，有待實驗……