FFT是一種DFT的高效算法，稱為快速傅立葉變換（fast Fourier transform），它根據離散傅氏變換的奇、偶、虛、實等特性，對離散傅立葉變換的算法進行改進獲得的。

　　FFT運算效率

　　使用STM32官方提供的DSP庫進行FFT，雖然在使用上有些不靈活（因為它是基4的FFT，所以FFT的點數必須是4^n），但其執行效率確實非常高效，看圖1所示的FFT運算效率測試數據便可見一斑。

　　如何使用STM32提供的DSP庫函數

　　1.下載STM32的DSP庫

　　大家可以從網上搜索下載得到STM32的DSP庫

　　2.添加DSP庫到自己的工程項目中

　　下載得到STM32的DSP庫之后，就可以將其添加到自己的工程項目中了。

　　其中，inc文件夾下的stm32_dsp.h和table_fft.h兩個文件是必須添加的。stm32_dsp.h是STM32的DSP庫的頭文件。src文件夾下的文件可以有選擇的添加（用到那個添加那個即可）。

　　3.模擬采樣數據

　　根據采樣定理，采樣頻率必須是被采樣信號最高頻率的2倍。這里，我要采集的是音頻信號，音頻信號的頻率范圍是20Hz到20KHz，所以我使用的采用頻率是44800Hz。那么在進行256點FFT時，將得到44800Hz / 256 = 175Hz的頻率分辨率。

　　為了驗證FFT運算結果的正確性，這里我模擬了一組采樣數據，并將該采樣數據存放到了long類型的lBufInArray數組中，且該數組中每個元素的高16位存儲采樣數據的實部，低16位存儲采樣數據的虛部（總是為0）。

　今天小編選擇了使用STM32f4提供的DSP庫這種方法來做fft的運算，下面我們我看下具體詳情：

　　STM32F4 dsp庫做FFT運算：

　　環境：iar 6.2

　　板子：STM32F4DISCOVERY

　　第一 首先下載官方的 STM32F4xx_DSP_StdPeriph_Lib_V1.0.0 沒有的同學請自己去官網下一個

　　DSP庫在 STM32F4xx_DSP_StdPeriph_Lib_V1.0.0\Libraries\CMSIS

　　然后我們使用IAR建立工作空間，這個教程到處都有，我就不說了在編譯器里面加入

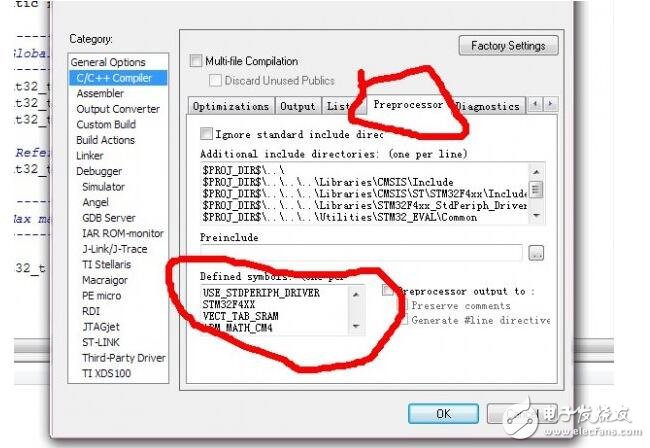
　　$PROJ_DIR$\。。\。。\。。\Libraries\CMSIS\DSP_Lib\Source

　　ARM_MATH_CM4

　　ARM_MATH_MATRIX_CHECK

　　ARM_MATH_ROUNDING

　　__FPU_PRESENT

　　__FPU_USED

　　這樣才可以使用DSP庫

　　注意 我的是IAR MDK貌似不是這樣的 。。。。。

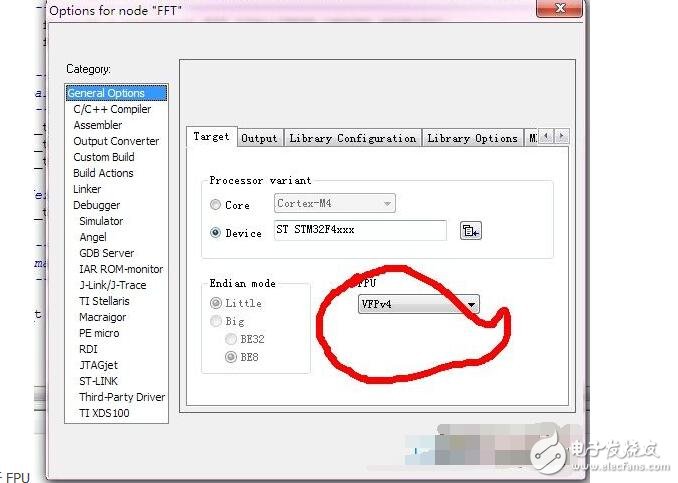
　　然后再編譯器里面打開 FPU

　　然后再你的EWARM 目錄下添加官方的例子文件

　　我們用的就是這幾個文件 STM32F4xx_DSP_StdPeriph_Lib_V1.0.0\Libraries\CMSIS\DSP_Lib\Examples\arm_fft_bin_example

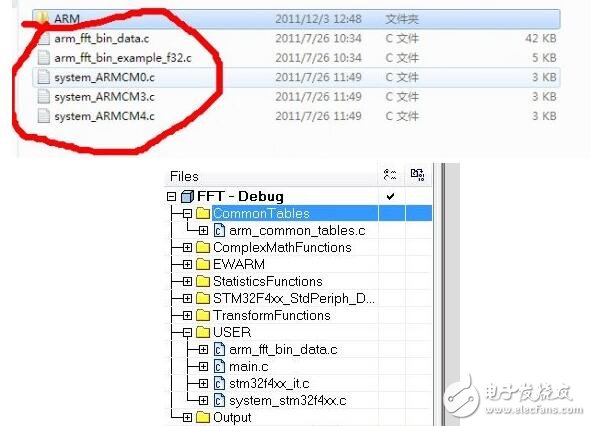
　　接著像我這樣加入這些組 在里面添加文件 文件在STM32F4xx_DSP_StdPeriph_Lib_V1.0.0\Libraries\CMSIS\DSP_Lib\Source添加，然后在IAR里面加入 arm_fft_bin_example_f32 這個就是官方的例子 和官方的數據 arm_fft_bin_data

　　連接下載

　　使用WATCH窗口可以看見值

　　然后 我講一下這幾個函數的作用

　　/* Initialize the CFFT/CIFFT module */

　　status = arm_cfft_radix4_init_f32（&S， fftSize，

　　ifftFlag， doBitReverse）; //這里是FFT的初始化

　　/* Process the data through the CFFT/CIFFT module */ //FFT計算的函數 注意 testInput_f32_10khz 這個數組 不能是const 因為計算值是覆蓋在這里面的

　　arm_cfft_radix4_f32（&S， testInput_f32_10khz）;

　　/* Process the data through the Complex Magnitude Module for // FFT出來的是復數 這里是把復數求模 得幅值

　　calculating the magnitude at each bin */

　　arm_cmplx_mag_f32（testInput_f32_10khz， testOutput，

　　fftSize）;

　　/* Calculates maxValue and returns corresponding BIN value */ //這里是求FFT出來數據模的最大值

　　arm_max_f32（testOutput， fftSize， &maxValue， &testIndex）;

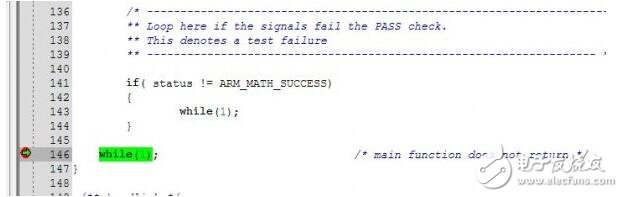
　　最后，如果你的運行到這一步 你就成功了