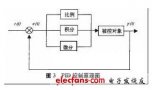
一、PID算法:
比例、積分、微分控制,簡稱PID控制,又稱PID調節;
二、應用環境:
當被控對象的結構和參數不能完全掌握,或得不到精確的數學模型時,控制理論的其它技術難以采用時,系統控制器的結構和參數必須依靠經驗和現場調試來確定;(由于賽道的參數事先未知,所以只能根據實時采集到的賽道數據控制小車沿著賽道行進)
三、PID算法應用實例
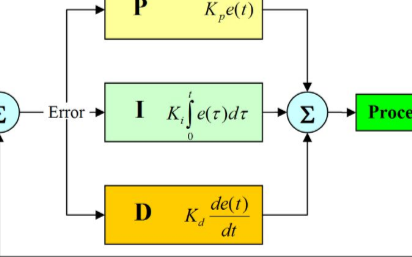
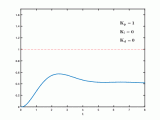
四、參數調整
PID控制器參數選擇的方法很多,例如試湊法、臨界比例度法、擴充臨界比例度法等。但是,對于PID控制而言,參數的選擇始終是一件非常煩雜的工作,需要經過不斷的調整才能得到較為滿意的控制效果。依據經驗,一般PID參數確定的步驟如下:
(1)確定比例系數Kp
確定比例系數Kp時,首先去掉PID的積分項和微分項,可以令Ti=0、Td=0,使之成為純比例調節。輸入設定為系統允許輸出最大值的60%~70%,比例系數Kp由0開始逐漸增大,直至系統出現振蕩;再反過來,從此時的比例系數Kp逐漸減小,直至系統振蕩消失。記錄此時的比例系數Kp,設定PID的比例系數Kp為當前值的60%~70%。
(2)確定積分時間常數Ti
比例系數Kp確定之后,設定一個較大的積分時間常數Ti,然后逐漸減小Ti,直至系統出現振蕩,然后再反過來,逐漸增大Ti,直至系統振蕩消失。記錄此時的Ti,設定PID的積分時間常數Ti為當前值的150%~180%。
(3) 確定微分時間常數Td
微分時間常數Td一般不用設定,為0即可,此時PID調節轉換為PI調節。如果需要設定,則與確定Kp的方法相同,取不振蕩時其值的30%。
(4) 系統空載、帶載聯調
對PID參數進行微調,直到滿足性能要求。
PID代碼
//定義變量
float Kp; //PI調節的比例常數
float Ti; //PI調節的積分常數
float T; //采樣周期
float Ki;
float ek; //偏差e[k]
float ek1; //偏差e[k-1]
float ek2; //偏差e[k-2]
float uk; //u[k]
signed int uk1; //對u[k]四舍五入取整
signed int adjust; //調節器輸出調整量
//變量初始化
Kp=4;
Ti=0.005;
T=0.001;
// Ki=KpT/Ti=0.8,微分系數Kd=KpTd/T=0.8,Td=0.0002,根據實驗調得的結果確定這些參數
ek=0;
ek1=0;
ek2=0;
uk=0;
uk1=0;
adjust=0;
int piadjust(float ek) //PI調節算法
{
if( gabs(ek)《0.1 )
{
adjust=0;
}
else
{
uk=Kp*(ek-ek1)+Ki*ek; //計算控制增量
ek1=ek;
uk1=(signed int)uk;
if(uk》0)
{
if(uk-uk1》=0.5)
{
uk1=uk1+1;
}
}
if(uk《0)
{
if(uk1-uk》=0.5)
{
uk1=uk1-1;
}
}
adjust=uk1;
}
return adjust;
}
下面是在AD中斷程序中調用的代碼。
。。。。。。。。。。。
else //退出軟啟動后,PID調節,20ms調節一次
{
EvaRegs.CMPR3=EvaRegs.CMPR3+piadjust(ek);//誤差較小PID調節穩住
if(EvaRegs.CMPR3》=890)
{
EvaRegs.CMPR3=890; //限制PWM占空比
}
}
下面是在AD中斷程序中調用的代碼。
。。。。。。。。。。。
else //退出軟啟動后,PID調節,20ms調節一次
{
EvaRegs.CMPR3=EvaRegs.CMPR3+piadjust(ek);//誤差較小PID調節穩住
if(EvaRegs.CMPR3》=890)
{
EvaRegs.CMPR3=890; //限制PWM占空比
}
}
 電子發燒友App
電子發燒友App








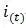
















評論