PID是比例-積分-微分控制的簡稱，也是一種控制算法，其特點(diǎn)是結(jié)構(gòu)改變靈活、技術(shù)成熟、適應(yīng)性強(qiáng)。

　　對一個(gè)控制系統(tǒng)而言，由于控制對象的精確數(shù)學(xué)模型難以建立，系統(tǒng)的參數(shù)經(jīng)常發(fā)生變化，運(yùn)用控制理論綜合分析要耗費(fèi)很大的代價(jià)，卻不能得到預(yù)期的效果，所以人們往往采用PID調(diào)節(jié)器，根據(jù)經(jīng)驗(yàn)在線整定參數(shù)，以便得到滿意的控制效果。隨著計(jì)算機(jī)特別是微機(jī)技術(shù)的發(fā)展，PID控制算法已能用微機(jī)簡單實(shí)現(xiàn)，由于軟件系統(tǒng)的靈活性，PID算法可以得到修正而更加完善。

　　PID參數(shù)的工程整定方法

　　數(shù)字PID調(diào)節(jié)器與模擬PID調(diào)節(jié)器控制思想完全一樣，只是實(shí)現(xiàn)的物理過程不同，數(shù)字PID調(diào)節(jié)器參數(shù)的整定方法也和模擬PID調(diào)節(jié)器基本相同，只是增加了自整定功能。

　　參數(shù)整定的方法很多，我們只介紹幾種工程上最常用的方法。最實(shí)用的是試湊法。

　　1、自整法

　　現(xiàn)在的數(shù)字調(diào)節(jié)器，大多采用了模糊控制技術(shù)進(jìn)行PID調(diào)節(jié)。

　　模糊控制基于專家知識或熟練操作者的成熟經(jīng)驗(yàn)，并可通過學(xué)習(xí)不斷更新。因而它具有智能性和自學(xué)習(xí)性，是一種人工智能調(diào)節(jié)方式。PID參數(shù)的自整功能，模擬專家操作，自動尋優(yōu)，整定出最佳參數(shù)，使之達(dá)到理想的控制效果。我們在使用調(diào)節(jié)器時(shí)，應(yīng)首先啟動自整功能，看一看整定的結(jié)果和控制效果，這是一個(gè)向?qū)＜蚁到y(tǒng)學(xué)習(xí)的過程。自整定結(jié)果，也不一定都是最佳參數(shù)，有時(shí)還需我們進(jìn)一步尋優(yōu)。關(guān)于啟動自整功能的方法，請閱讀有關(guān)的說明書，非常簡單。

　　2、逐試法

　　將PID參數(shù)之一增加或減少30～50%，如果控制效果變好，則繼續(xù)增加或減少該參數(shù)，否則往反方向調(diào)整，直到效果滿足要求。

　 ??3、臨界值整定性

? ? ? ?①比例+積分調(diào)節(jié)器 a、積分時(shí)間置于最大； b、置TD=0；

　　c、從一個(gè)比較大的比例帶逐步降低，每降低一次等待一定的時(shí)間，觀察記錄表上或記錄紙上被控參量的記錄曲線，直至記錄曲線出現(xiàn)周期性振蕩，然后在這一點(diǎn)上再加大比例帶，直到不出現(xiàn)振蕩；

　　D、減少積分時(shí)間，每減一次同樣等待一定的時(shí)間，觀察記錄曲線，當(dāng)它低于由過程的滯后特性所決定的某個(gè)臨界值時(shí)，曲線又出現(xiàn)周期性振蕩，然后在這點(diǎn)上緩慢地加大積分時(shí)間直至振蕩停止。

　　②比例+積分+微分調(diào)節(jié)器

? ? ? ? a、積分時(shí)間置于最大；
?
? ? ? ? b、微分時(shí)間置于最小；

　　c、用上方法減小比例帶至周期性振蕩出現(xiàn)；

　　d、加大微分時(shí)間，使周期性振蕩停止，再減小比例帶，使振蕩重新出現(xiàn)，再加大微分時(shí)間，使振蕩停止，重復(fù)上述過程至加大微分時(shí)間后振蕩不再停止。再增大比例帶至周期性振蕩停止。

　　E、取積分時(shí)間為微分時(shí)間的2～5倍，如果周期性振蕩出現(xiàn)，加大積分時(shí)間至振蕩停止。

　　4、經(jīng)驗(yàn)整定法

　　根據(jù)PID控制原理和系統(tǒng)的特性，結(jié)合自己的經(jīng)驗(yàn)，直接設(shè)置PID參數(shù)，然后再根據(jù)控制效果做進(jìn)一步的修改。

　　當(dāng)調(diào)節(jié)器輸出變化很小，而引起測量值（被控參量）變化較大時(shí)，應(yīng)將比例帶置于較大的數(shù)值，反之亦然。當(dāng)調(diào)節(jié)器輸出變化，很快引起被控參量的變化，則積分和微分時(shí)間的整定就應(yīng)較小，對于快速的流量系統(tǒng)則可以不加入微分運(yùn)算，反之亦然。熟悉系統(tǒng)的特性是整定PID參數(shù)的關(guān)鍵。最后分析兩個(gè)溫度調(diào)節(jié)系統(tǒng)，加深對上述內(nèi)容的理解。

　　例1：果凍條封口溫控系統(tǒng)，采用佳能電子CNG-5181智能數(shù)字調(diào)節(jié)儀出廠時(shí)參數(shù)設(shè)定為P=20，I=130，d=30，置設(shè)定值SV=150℃，PV達(dá)到SV時(shí)，啟動自整定功能，大約在20分鐘左右，自整結(jié)束。P=15，I=236，d=59。進(jìn)入PID控制后，PV很快穩(wěn)定在上150℃上，當(dāng)設(shè)定值改為155℃，PV很快又穩(wěn)定在155℃，動靜態(tài)品質(zhì)均非常理想，實(shí)際上采用出廠設(shè)定參數(shù)值也能獲得滿意的控制效果。

　　例2，聯(lián)苯鍋爐用于化纖紡絲管道伴熱，工藝溫度為290℃～300℃，溫控器選用日本島電公司SR74型PID自整定溫控儀，出廠設(shè)定值為P=3，I=120，D=30，在該參數(shù)下，溫度波動較大為295℃±3℃。啟動自整定功能，約1小時(shí)后，整定出的PID參數(shù)為P=0.3，I=1168，D=292，顯示溫度始終為295℃，改變設(shè)定值為300℃時(shí)。顯示溫度又始終為300℃。

　　點(diǎn)評：果凍條封口溫控系統(tǒng)屬于小型溫控系統(tǒng)，系統(tǒng)靈敏度高，熱慣性小，滯后時(shí)間短，所以比例帶較大，積分、微分時(shí)間常數(shù)均比較小。或者說比例、微分作用較弱，積分作用較強(qiáng)。例2中的溫控系統(tǒng)屬于大型的調(diào)節(jié)系統(tǒng)，靈敏度低，熱慣性大，滯后時(shí)間長，所以整定出的PID參數(shù)和例1相反，比例帶較小，積分和微分時(shí)間常數(shù)均較大，且TI≈4TD。

　　1）臨界比例度法

　　這是目前使用較廣的一種方法，具體作法如下：

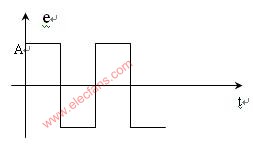
　　先在純比例作用下（把積分時(shí)間放到最大，微分時(shí)間放到零），在閉合的調(diào)節(jié)系統(tǒng)中，從大到小地逐漸地改變調(diào)節(jié)器的比例度，就會得到一個(gè)臨界振蕩過程，如圖8所示。這時(shí)的比例度叫臨界比例度δk，周期為臨界振蕩周期Tk。記下δk和Tk，然后按表1的經(jīng)驗(yàn)公式來確定調(diào)節(jié)器的各參數(shù)值。

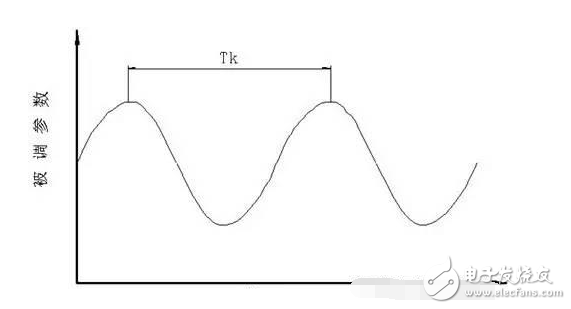
　　表1 臨界比例度法數(shù)據(jù)表

　　這種方法在下面兩種情況下不宜采用：

　　a）臨界比例度過小，因?yàn)檫@時(shí)候調(diào)節(jié)閥很容易處于全開及全關(guān)位置，對于工藝生產(chǎn)不利，舉例來說，對于一個(gè)用燃料油（或瓦斯）加熱的爐子，如δ很小，接近雙位調(diào)節(jié)，將一會兒熄火，一會兒煙囪濃煙直沖。

　　b）工藝上約束條件較嚴(yán)格時(shí)，因?yàn)檫@時(shí)候如達(dá)到等幅振蕩，將影響生產(chǎn)的安全運(yùn)行。

　　2）衰減曲線法

　　臨界比例度法是要系統(tǒng)等幅振蕩，還要多次試湊，而用衰減曲線法較簡單，一般又有兩種方法。

　　（1）4：1衰減曲線法

　　使系統(tǒng)處于純比例作用下，在達(dá)到穩(wěn)定時(shí)，用改變給定值的辦法加入階躍干擾，觀察記錄曲線的衰減比，然后逐漸從大到小改變比例度，使出現(xiàn)4：1的衰減比為止，如下圖所示。記下此時(shí)的比例度δs和Ts的值，再按表2的經(jīng)驗(yàn)公式來確定PID數(shù)值。

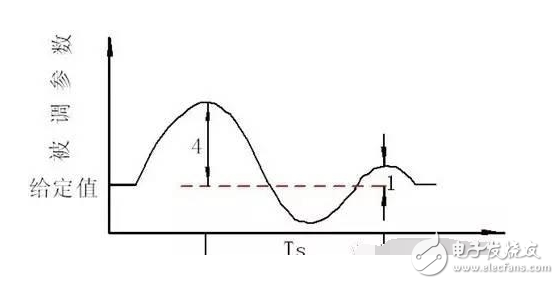
　　表2 4：1衰減曲線法數(shù)據(jù)表

　　（2）10：1衰減曲線法

　　有的過程，4：1衰減仍嫌振蕩過強(qiáng)，可采用10：1衰減曲線法。方法同上，得到10：1衰減曲線，記下此時(shí)的比例度δ＇s和上升時(shí)間T＇s，再按表3的經(jīng)驗(yàn)公式來確定PID的數(shù)值。衰減曲線如下圖所示。

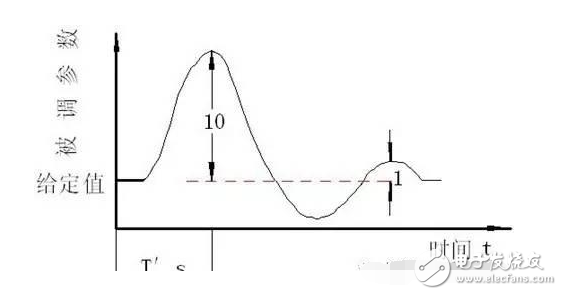
　　表3 10：1衰減曲線法數(shù)據(jù)表

　　采用衰減曲線法必須注意幾點(diǎn)：

　　a）加給定干擾不能太大，要根據(jù)生產(chǎn)操作要求來定，一般在5%左右，也有例外的情況。

　　b）必須在工藝參數(shù)穩(wěn)定的情況下才能加給定干擾，否則得不到正確得δs、Ts、或δ＇s和T＇s值。

　　c）對于反應(yīng)快的系統(tǒng)，如流量、管道壓力和小容量的液位調(diào)節(jié)等，要在記錄紙上嚴(yán)格得到4：1衰減曲線較困難，一般以被調(diào)參數(shù)來回波動兩次達(dá)到穩(wěn)定，就近似地認(rèn)為達(dá)到4：1衰減過程了。

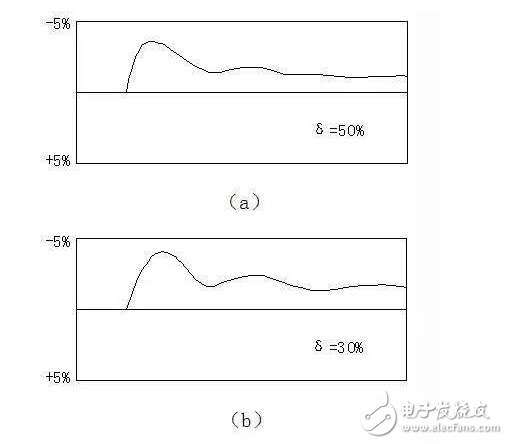
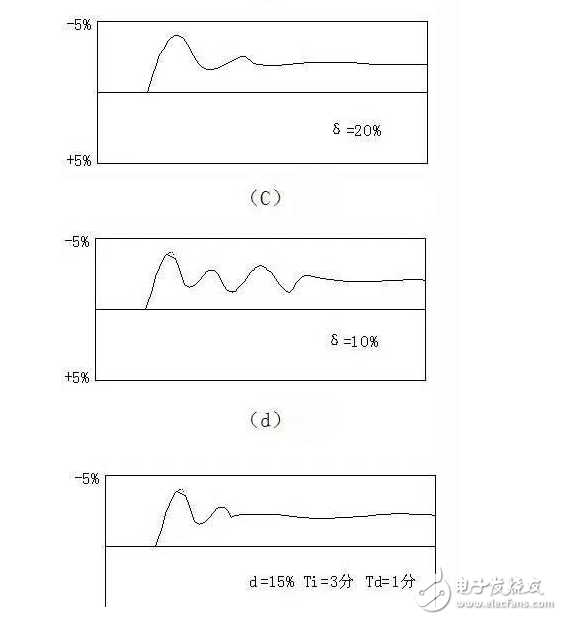
　　下面舉一個(gè)現(xiàn)場整定的例子。在某塔頂溫度調(diào)節(jié)系統(tǒng)中，被調(diào)參數(shù)是塔頂溫度，工藝允許波動為＜4℃，調(diào)節(jié)參數(shù)是回流量。在整定過程中，考慮到對象滯后較大，反應(yīng)較慢的情況，δ的選擇從50%開始湊試起，此時(shí)在階躍作用下（給定值降低2%）的過渡過程曲線見下圖（a）。此時(shí)調(diào)節(jié)時(shí)間長，不起振蕩，于是將比例度減少，δ=30%、20%、及10%時(shí)的曲線見（b）、（c）、（d）。顯然，20%的情況最好，衰減比接近4：1，Ts=10分。

　　按4：1衰減曲線法數(shù)據(jù)表定出整定參數(shù)：

　　δ=0.8·δs=16%；

　　Ti=0.3·Ts=3分；

　　Td=0.1·Ts=1分。

　　投運(yùn)時(shí)，先將δ放在較大的數(shù)值，把Ti從大減少到3分，把Td從小到大逐步放大到1分，然后把δ拉到15%，（如果在δ=15%的條件下很快地把Td放到1分，調(diào)節(jié)器的輸出會劇烈變化）。再對系統(tǒng)加2% 的給定值變化時(shí)，仍產(chǎn)生4：1衰減過程，見圖（e）所示，調(diào)節(jié)質(zhì)量顯著改善，超調(diào)量小于1℃，調(diào)節(jié)時(shí)間為6.5分。

　　3）經(jīng)驗(yàn)試湊法

　　這是在生產(chǎn)實(shí)踐中所總結(jié)出來的方法，目前應(yīng)用最為廣泛，其步驟簡述如下：

　　（1）確定KP

　　可用“優(yōu)選法”，詳見下表

　　表4 優(yōu)選法確定KP

　　（2）看曲線，調(diào)參數(shù)，根據(jù)操作經(jīng)驗(yàn)，看曲線的形狀，直接在閉合的調(diào)節(jié)系統(tǒng)中逐步反復(fù)試湊，一直得到滿意數(shù)據(jù)。

　　在實(shí)踐中，把具體整定的方法總結(jié)了幾段順口溜：

　　參數(shù)整定找最佳，從大到小順次查，先是比例后積分，最后才把微分加；曲線振蕩很頻繁，比例度值要放大， //比例度放大即比例系數(shù)KP要減小。曲線漂浮繞大彎，比例度值應(yīng)減小；曲線偏離回復(fù)慢，積分時(shí)間往下降，曲線振蕩周期長，積分時(shí)間再加長；曲線振蕩頻率快，先把微分降下來，動差大來波動慢，微分時(shí)間應(yīng)加長；理想曲線兩個(gè)波，前高后低四比一，一看二調(diào)多分析，調(diào)節(jié)質(zhì)量不會低。

　　第一段講的是整定順序，δ和Ti都是從大到小逐步加上去，微分是最后才考慮的。第二段講的是比例度如何整定。第三段講的是積分時(shí)間如何整定。第四段講的是微分時(shí)間如何整定。第五段講的是標(biāo)準(zhǔn)。

　　上面這種方法步驟是先加δ，再加Ti，最后才加Td。應(yīng)用中較穩(wěn)妥。

　　另一種方法是先從表列范圍內(nèi)取Ti的某個(gè)數(shù)值，如果需要微分，則取Td=（1/3~1/4）Ti，然后對δ進(jìn)行試湊，也能較快地達(dá)到要求。

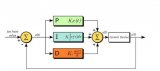
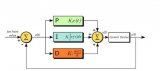
　　常用PID控制參數(shù)的經(jīng)驗(yàn)值如下圖所示。

　　PID算法的定義：

　　P：比例控制項(xiàng)。 I：積分控制項(xiàng)。 D：微分控制項(xiàng)。

　　設(shè)當(dāng)前輸出量為U，我們的期望值或是設(shè)定值為U0，則可得當(dāng)前時(shí)刻誤差：E=U-U0;

　　PID算法即是對誤差量E及E的歷史進(jìn)行某種線性組合得到控制量的算法。

　　一般形式：

　　Up=P*E;

　　Ui=i*（E+E_1+E_2+.。。） E_n為之前的第n次誤差．

　　Ud=i*（E-E_1）

　　U=Up+Ui+Ud; U為PID控制輸出量．

　　上式中Ui的計(jì)算不太方便，長時(shí)間單方向的累加將可能出現(xiàn)溢出，于是將上式改為如下所示的增量形式：

　　Up=p*（E-E_1） 比例項(xiàng)增量

　　Ui=i*（E-2*E_1+E_2） 微分項(xiàng)增量

　　Ud=i*E 積分項(xiàng)增量

　　U=Uout_1+Up+Ui+Ud U為PID控制輸出量，Uout_1為前次PID輸出值

　　Uout=U 保存本次值

　　對于上面的公式或理論，便可得到相應(yīng)的C語言程序：

　　//======================定義PID結(jié)構(gòu)=========================

　　static float MinValue; //最大值限制

　　static float MaxValue; //最小值限制

　　static float CurrentValue; //當(dāng)前采樣值

　　static struct PID{

　　float Ki; //定義積分常數(shù)

　　float Kp; //定義比例常數(shù)

　　float Kd; //定義微分常數(shù)

　　float E_2; //存儲前前次誤差

　　float E_1; //存諸前次誤差

　　float E; //存儲本次誤差

　　float OutPut; //本次輸出量

　　float ValueSet; //設(shè)定值或期望值

　　}Control;

　　//===========================PID計(jì)算函數(shù)=====================

　　void PidWork（） {

　　float Up，Ud，Ui;

　　Control.E=CurrentValue-Control.ValueSet; //得到本次誤差

　　Up =Control.Kp*（Control.E-Control.E_1）; //得到比例項(xiàng)

　　Ud=Control.Kd*（Control.E-2*Control.E_1+Control.E_2）; //得到微分項(xiàng)

　　Ui=Control.Ki*Control.E; //得到積分項(xiàng)

　　Control.E_2=Control.E_1; //歷史存儲

　　Control.E_1=Control.E;

　　Control.OutPut+=Up+Ud+Ui; //計(jì)算增量和

　　if（Control.OutPut

　　else if（Control.OutPut》MaxValue）Control.OutPut=MaxValue;

　　}

　　//==========================初始化速度=========================

　　void PidInit（） {

　　MinValue=0;

　　MaxValue=1000;

　　CurrentValue=0;

　　Control.Kp=-6;

　　Control.Ki=-1.5;

　　Control.Kd=-0.5;

　　Control.E=0;

　　Control.E_2=0;

　　Control.E_1=0;

　　Control.ValueSet=100;

　　Control.OutPut=0;

　　}

　　以上三個(gè)函數(shù)為PID的主體函數(shù)，也是萬用PID函數(shù)．代碼量已經(jīng)相當(dāng)精簡了。注意上面的PID初始化函數(shù)中有Kp，Ki，Kd的符號一定要正確，否則輸出量方向相反，后果不堪設(shè)想！！！

　　附上一段完整代碼：

　　#include

　　struct _pid {

　　int pv; /*integer that contains the process value*/

　　int sp; /*integer that contains the set point*/

　　float integral;

　　float pgain;

　　float igain;

　　float dgain;

　　int deadband;

　　int last_error;

　　};

　　struct _pid warm，*pid;

　　int process_point， set_point，dead_band;

　　float p_gain， i_gain， d_gain， integral_val，new_integ;;

　　/*------------------------------------------------------------------------

　　pid_init

　　DESCRIPTION This function initializes the pointers in the _pid structure

　　to the process variable and the setpoint. *pv and *sp are

　　integer pointers.

　　------------------------------------------------------------------------*/

　　void pid_init（struct _pid *warm， int process_point， int set_point）

　　{

　　struct _pid *pid;

　　pid = warm;

　　pid-》pv = process_point;

　　pid-》sp = set_point;

　　}

　　/*------------------------------------------------------------------------

　　pid_tune

　　DESCRIPTION Sets the proportional gain （p_gain）， integral gain （i_gain），

　　derivitive gain （d_gain）， and the dead band （dead_band） of

　　a pid control structure _pid.

　　------------------------------------------------------------------------*/

　　void pid_tune（struct _pid *pid， float p_gain， float i_gain， float d_gain， int dead_band）

　　{

　　pid-》pgain = p_gain;

　　pid-》igain = i_gain;

　　pid-》dgain = d_gain;

　　pid-》deadband = dead_band;

　　pid-》integral= integral_val;

　　pid-》last_error=0;

　　}

　　/*------------------------------------------------------------------------

　　pid_setinteg

　　DESCRIPTION Set a new value for the integral term of the pid equation.

　　This is useful for setting the initial output of the

　　pid controller at start up.

　　------------------------------------------------------------------------*/

　　void pid_setinteg（struct _pid *pid，float new_integ）

　　{

　　pid-》integral = new_integ;

　　pid-》last_error = 0;

　　}

　　/*------------------------------------------------------------------------

　　pid_bumpless

　　DESCRIPTION Bumpless transfer algorithim. When suddenly changing

　　setpoints， or when restarting the PID equation after an

　　extended pause， the derivative of the equation can cause

　　a bump in the controller output. This function will help

　　smooth out that bump. The process value in *pv should

　　be the updated just before this function is used.

　　------------------------------------------------------------------------*/

　　void pid_bumpless（struct _pid *pid）

　　{

　　pid-》last_error = （pid-》sp）-（pid-》pv）;

　　}

　　/*------------------------------------------------------------------------

　　pid_calc

　　DESCRIPTION Performs PID calculations for the _pid structure *a. This function uses the positional form of the pid equation， and incorporates an integral windup prevention algorithim. Rectangular integration is used， so this function must be repeated on a consistent time basis for accurate control.

　　RETURN VALUE The new output value for the pid loop.

　　USAGE #include ‘control.h’*/

　　float pid_calc（struct _pid *pid）

　　{

　　int err;

　　float pterm， dterm， result， ferror;

　　err = （pid-》sp） - （pid-》pv）;

　　if （abs（err） 》 pid-》deadband）

　　{

　　ferror = （float） err; /*do integer to float conversion only once*/

　　pterm = pid-》pgain * ferror;

　　if （pterm 》 100 || pterm 《》

　　{

　　pid-》integral = 0.0;

　　}

　　else

　　{

　　pid-》integral += pid-》igain * ferror;

　　if （pid-》integral 》 100.0）

　　{

　　pid-》integral = 100.0;

　　}

　　else if （pid-》integral 《 0.0）=“” pid-=“”》integral = 0.0;

　　}

　　dterm = （（float）（err - pid-》last_error）） * pid-》dgain;

　　result = pterm + pid-》integral + dterm;

　　}

　　else result = pid-》integral;

　　pid-》last_error = err;

　　return （result）;

　　}

　　void main（void）

　　{

　　float display_value;

　　int count=0;

　　pid = &warm;

　　// printf（‘Enter the values of Process point， Set point， P gain， I gain， D gain \n’）;

　　// scanf（‘%d%d%f%f%f’， &process_point， &set_point， &p_gain， &i_gain， &d_gain）;

　　process_point = 30;

　　set_point = 40;

　　p_gain = （float）（5.2）;

　　i_gain = （float）（0.77）;

　　d_gain = （float）（0.18）;

　　dead_band = 2;

　　integral_val =（float）（0.01）;

　　printf（‘The values of Process point， Set point， P gain， I gain， D gain \n’）;

　　printf（‘ %6d %6d %4f %4f %4f\n’， process_point， set_point， p_gain， i_gain， d_gain）;

　　printf（‘Enter the values of Process point\n’）;

　　while（count《》

　　{

　　scanf（‘%d’，&process_point）;

　　pid_init（&warm， process_point， set_point）;

　　pid_tune（&warm， p_gain，i_gain，d_gain，dead_band）;

　　pid_setinteg（&warm，0.0）; //pid_setinteg（&warm，30.0）;

　　//Get input value for process point

　　pid_bumpless（&warm）;

　　// how to display output

　　display_value = pid_calc（&warm）;

　　printf（‘%f\n’， display_value）;

　　//printf（‘\n%f%f%f%f’，warm.pv，warm.sp，warm.igain，warm.dgain）;

　　count++;

　　}

　　}