一、霍夫曼編碼介紹
霍夫曼編碼(Huffman Coding)是一種編碼方式,是一種用于無損數據壓縮的熵編碼(權編碼)算法。
霍夫曼編碼是可變字長編碼(VLC)的一種。 Huffman于1952年提出一種編碼方法,該方法完全依據字符出現概率來構造異字頭的平均長度最短的碼字,有時稱之為最佳編碼,一般就稱Huffman編碼。下面引證一個定理,該定理保證了按字符出現概率分配碼長,可使平均碼長最短。
定理:在變字長編碼中,如果碼字長度嚴格按照對應符號出現的概率大小逆序排列,則其平 均碼字長度為最小。
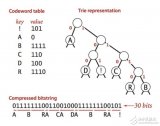
霍夫曼編碼的具體方法:先按出現的概率大小排隊,把兩個最小的概率相加,作為新的概率 和剩余的概率重新排隊,再把最小的兩個概率相加,再重新排隊,直到最后變成1。每次相 加時都將“0”和“1”賦與相加的兩個概率,讀出時由該符號開始一直走到最后的“1”, 將路線上所遇到的“0”和“1”按最低位到最高位的順序排好,就是該符號的霍夫曼編碼。
二、霍夫曼編碼特點
1) 編出來的碼都是異字頭碼,保證了碼的唯一可譯性。
2) 由于編碼長度可變。因此譯碼時間較長,使得霍夫曼編碼的壓縮與還原相當費時。
3) 編碼長度不統一,硬件實現有難度。
4) 對不同信號源的編碼效率不同,當信號源的符號概率為2的負冪次方時,達到100%的編碼效率;若信號源符號的概率相等,則編碼效率最低。
5) 由于0與1的指定是任意的,故由上述過程編出的最佳碼不是唯一的,但其平均碼長是一樣的,故不影響編碼效率與數據壓縮性能。
三、Huffman霍夫曼編碼的壓縮原理
我們把文件中一定位長的值看作是符號,比如把8位長的256種值,也就是字節的256種值看作是符號。我們根據這些符號在文件中出現的頻率,對這些符號重新編碼。對于出現次數非常多的,我們用較少的位來表示,對于出現次數非常少的,我們用較多的位來表示。這樣一來,文件的一些部分位數變少了,一些部分位數變多了,由于變小的部分比變大的部分多,所以整個文件的大小還是會減小,所以文件得到了壓縮。
四、Huffman霍夫曼壓縮編碼算法實現分析
哈夫曼編碼Huffman方法于1952年問世,迄今為止仍經久不衰,廣泛應用于各種數據壓縮技術中,且仍不失為熵編碼中的最佳編碼方法,deflate等壓縮算法也是結合了huffman算法的。
采用霍夫曼編碼時有兩個問題值得注意:
①霍夫曼碼沒有錯誤保護功能,在譯碼時,如果碼串中沒有錯誤,那么就能一個接一個地正確譯出代碼。但如果碼串中有錯誤,哪僅是1位出現錯誤,不但這個碼本身譯錯,更糟糕的是一錯一大串,全亂了套,這種現象稱為錯誤傳播(error propagation)。計算機對這種錯誤也無能為力,說不出錯在哪里,更談不上去糾正它。
②霍夫曼碼是可變長度碼,因此很難隨意查找或調用壓縮文件中間的內容,然后再譯碼,這就需要在存儲代碼之前加以考慮。盡管如此,霍夫曼碼還是得到廣泛應用。
/*
霍夫曼編碼模型:思想是壓縮數據出現概率高的用短編碼,出現概率低的用長編碼,且每個字符編碼都不一樣。
壓縮數據單個字符出現的概率抽象為葉子節點的權值,huffman樹葉子節點到根節點的編碼(是父節點左子節點那么填0,否則填1)
作為字符的唯一編碼。
實現時候需要注意的規則:
1)最左的放置在左邊,作為父節點的左節點。
2)每次都從沒有設置父節點的所用節點中(葉子和分支節點一樣對待),從數組小下標到大下標優先順序遍歷。
3)當前搜尋的次數i + n作為新生成的分支節點的數組下標。
實現的過程和具體算法思想:
兩個數據結構:
一個是huffman樹節點結構體,一個是從霍夫曼樹葉子節點編碼的結構體。
兩個處理過程:
1)建立huffman樹:
基本思想是:對于沒有設置父節點的節點集選出最小的兩個,最小的放置在左邊,次小的放置在右邊
設置好父節點和左右子節點關系,方便獲得霍夫曼編碼。
2) 從huffman樹得到葉子節點的huffman編碼:
基本思想:對于建立好的Huffman樹的每個葉子節點,由編碼的數組的末端也是從葉子節點最底端,往上遍歷
如果是父節點的左節點那么用編碼數組填1,如果是父節點的右節點那么編碼數組填0,一直往上追溯到根節點。
*/
// 以下是實現的代碼,在win32編譯通過。
#include “stdafx.h”
#define MAXCODELEN 7
#define MAXWEIGHT 10000
struct tagHuffmanNode
{
int m_nWeight;
int m_nParent;
int m_nLChild;
int m_nRChild;
};
struct tagHuffmanCode
{
int m_nWeight;
int m_nStart;
int m_nBit[MAXCODELEN];
};
void Huffman(int w[], int n, tagHuffmanNode ht[], tagHuffmanCode hc[])
{
int nTotalCount = 2 * n - 1;
// 初始化填充好ht的所有權值,包括葉子節點和分支節點
for(int i = 0; i 《 nTotalCount; i++)
{
if( i 《 n)
{
ht[i].m_nWeight = w[i];
}
else
{
ht[i].m_nWeight = 0;
}
ht[i].m_nParent = 0;
ht[i].m_nLChild = ht[i].m_nRChild = -1;
}
// 構造一顆huffman樹,設置n-1個分支節點(非葉子),
// 基本思想是:對于沒有設置父節點的節點集選出最小的兩個,最小的放置在左邊,次小的放置在右邊
// 設置好父節點和左右子節點關系,方便獲得霍夫曼編碼
int nCurMinWeight,nCurSecondMinWeight;
int nCurLeftChild, nCurRightChild;
for( int i = 0; i 《 n-1; i++)
{
nCurMinWeight = nCurSecondMinWeight = MAXWEIGHT;
nCurLeftChild = nCurRightChild = 0;
// 確定一個分支節點,需要對n + i個節點進行篩選
for( int j = 0; j 《 n + i; j++)
{
if( ht[j].m_nWeight 《 nCurMinWeight && ht[j].m_nParent == 0)
{
nCurSecondMinWeight = nCurMinWeight;
nCurRightChild = nCurLeftChild;
nCurMinWeight = ht[j].m_nWeight;
nCurLeftChild = j;
}
else if(ht[j].m_nWeight 《 nCurSecondMinWeight && ht[j].m_nParent == 0)
{
nCurSecondMinWeight = ht[j].m_nWeight;
nCurRightChild = j;
}
}
// 得到分支節點,設置節點關系
ht[n + i].m_nLChild = nCurLeftChild;
ht[n + i].m_nRChild = nCurRightChild;
ht[n + i].m_nWeight =nCurMinWeight + nCurSecondMinWeight;
ht[nCurLeftChild].m_nParent = n + i;
ht[nCurRightChild].m_nParent = n + i;
}
// 測試用
/*for(int i = 0; i 《 nTotalCount; i++)
{
printf(“--------------------------------\n”);
printf(“ht[%d].m_nWeight: %d\n”, i, ht[i].m_nWeight);
printf(“ht[%d].m_nParent: %d\n”, i, ht[i].m_nParent);
printf(“ht[%d].m_nLChild: %d\n”, i, ht[i].m_nLChild);
printf(“ht[%d].m_nRChild: %d\n”, i, ht[i].m_nRChild);
}*/
// 記錄下來每個葉子節點的huffman編碼
// 基本思想:對于建立好的Huffman樹的每個葉子節點,由編碼的數組的末端也是從葉子節點最底端,往上遍歷
// 如果是父節點的左節點那么用編碼數組填1,如果是父節點的右節點那么編碼數組填0,一直往上追溯到根節點。
for(int k = 0; k 《 n; k++)
{
hc[k].m_nWeight = ht[k].m_nWeight;
hc[k].m_nStart = n - 1;// start等于最大的值
int nChild = k;
int nParent = ht[k].m_nParent;
while(nParent != 0)
{
if(nChild == ht[nParent].m_nLChild)
{
hc[k].m_nBit[hc[k].m_nStart] = 0;
}
else if(nChild == ht[nParent].m_nRChild)
{
hc[k].m_nBit[hc[k].m_nStart] = 1;
}
hc[k].m_nStart--;
nChild = nParent;
nParent = ht[nChild].m_nParent;
}
// 因為遞減了需要增加,得到正確的起始下標
hc[k].m_nStart++;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int nDataNum = 7;
int nWeigt[] = {4, 2, 6, 8, 3, 2, 1};
const int nMaxLen = 2 * nDataNum - 1;
tagHuffmanNode *ht = new tagHuffmanNode[nMaxLen];
tagHuffmanCode *hc = new tagHuffmanCode[nDataNum];
Huffman(nWeigt, nDataNum, ht, hc);
for(int i = 0; i 《 7; i++)
{
printf(“index: %d, weight: %d, hc[%d].m_nBit: ”, i, hc[i].m_nWeight, i);
for(int j = hc[i].m_nStart; j 《 7; j++)
{
printf(“%d”, hc[i].m_nBit[j]);
}
printf(“\n”);
}
delete []ht;
delete []hc;
while(1);
return 0;
}
 電子發燒友App
電子發燒友App























評論