微軟研究院最近提出了一個新的 LLM 自回歸基礎架構 Retentive Networks (RetNet)[1,4],該架構相對于 Transformer 架構的優勢是同時具備:訓練可并行、推理成本低和良好的性能,不可能三角。
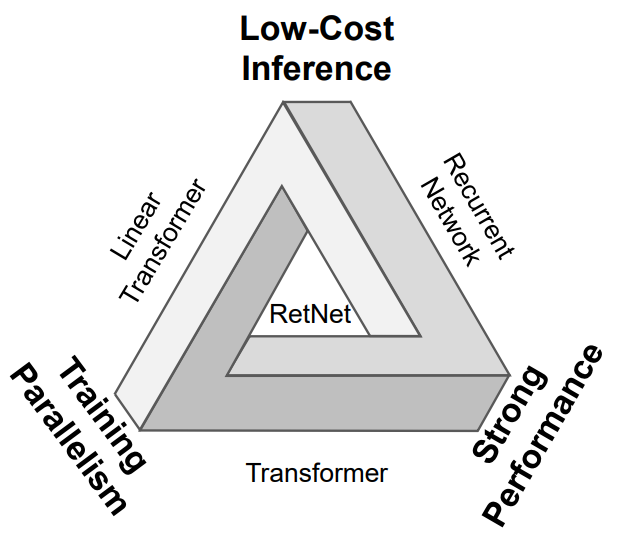
論文中給出一個很形象的示意圖,RetNet 在正中間表示同時具備三個優點,而其他的架構 Linear Transformer、Recurrent Network 和 Transformer 都只能同時具備其中兩個有點。
接下來看一下論文給出的 RetNet 和 Transformer 的對比實驗結果:
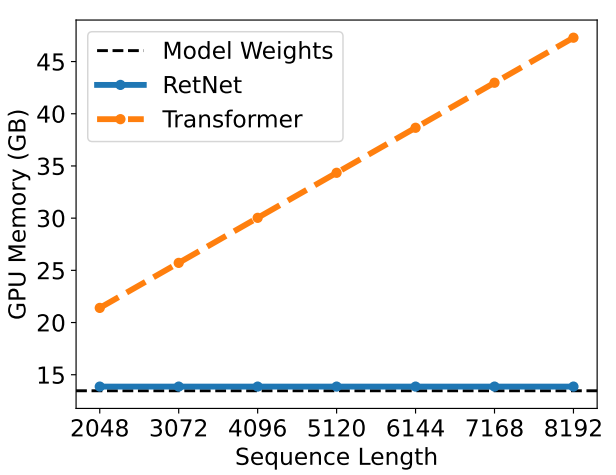
當輸入序列長度增加的時候,RetNet 的 GPU 顯存占用一直是穩定的和權值差不多,而 Transformer 則是和輸入長度成正比。
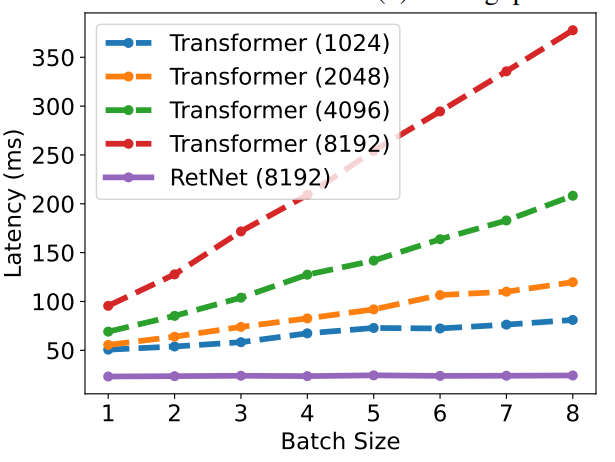
首先看紅色線和紫色線,都是輸入長度在 8192 下,RetNet 和 Transformer 推理延時的對比。
可以看到當 batch size 增加的時候, RetNet 的推理延時也還是很穩定,而 Transformer 的推理延時則是和 batch size 成正比。
而 Transformer 即使是輸入長度縮小到 1024 ,推理延時也還是比 RetNet 要高。
RetNet 架構解讀
RetNet 架構和 Transformer 類似,也是堆疊 層同樣的模塊,每個模塊內部包含兩個子模塊:一個 multi-scale retention(MSR)和一個 feed-forward network (FFN)。
下面詳細解讀一下這個 retention 子模塊。
首先給定一個輸入序列 :
其中 表示序列的長度。然后輸入序列首先經過 embedding 層得到詞嵌入向量:
其中 表示隱含層的維度。
Retention 機制
首先對給定輸入詞嵌入向量序列 中的每個時間步 的向量 都乘以權值 得到 :
然后同樣有類似 Transformer 架構的 Q 和 K 的投影:
其中 是需要學習的權值。
接著假設現在有一個序列建模的問題,通過狀態 將 映射為 向量。首先來看論文中給出的映射方式定義:
其中 是一個矩陣, 表示時間步 對應的 投影則 。同樣 表示時間步 對應的 投影。
那么上面公式中的 計算公式是怎么得出來呢,下面詳細解釋一下,首先將 展開:
其中 表示單位矩陣(主對角線元素為1,其余元素為0的方陣)。然后我們假定 為初始狀態元素為全0的矩陣,則有:
再繼續上述推導過程:
所以根據上述推導過程和條件歸納可得:
然后我們來看一下 矩陣是什么,論文中定義了 是一個可對角化的矩陣,具體定義為:
其中 都是 維的向量, 是一個可逆矩陣,而要理解 首先得復習一下歐拉公式 [2]:
其中 表示任意實數, 是自然對數的底數, 是復數中的虛數單位,也可以表示為實部 ,虛部 的一個復數,歐拉公式[2]建立了指數函數、三角函數和復數之間的橋梁。
而這里 是一個 維向量:
則 也就是將向量元素兩兩一組表示分別表示為復數的實部和虛部:
然后 就是一個對角矩陣,對角元素的值就對應將 和 轉成復數向量相乘再將結果轉回實數向量的結果。
關于復數向量相乘可以參考文章:?
一文看懂 LLaMA 中的旋轉式位置編碼(Rotary Position Embedding)
現在我們知道了矩陣 的構成就能得到:
這里因為 是可逆矩陣則有性質
其中 為單位矩陣,則將 次方展開:
就是 個 矩陣相乘,中間相鄰的 都消掉了,所以可得:
然后我們回到計算 的公式:
接著論文中提出把 吸收進 和 也就是 和 分別用 和 替代當作學習的權值,那么可得:
接著將公式簡化,將 改為一個實數常量,那么可得:
在繼續推導前,先來仔細看一下 ,借助歐拉公式展開:
然后復習一下三角函數的性質[3]:
則有:
轉為復數形式表示就是:
剛好就對應 的共軛
所以可得:
其中 表示共軛轉置操作。
Retention 的訓練并行表示
首先回顧單個時間步 的輸出 的計算公式如下:
而所有時間步的輸出是可以并行計算的,用矩陣形式表達如下:
其中 ,而 表示兩個矩陣逐元素相乘, 和 每一行對應一個時間步的 q 和 k 向量。
而 每一行對應向量 。 就是對應 矩陣的共軛,也就是將 矩陣每一行改為復數的共軛形式。
而 矩陣是一個下三角矩陣,其中第 行第 列的元素計算方式:
Retention 的推理循環表示
推理階段的循環表示論文中定義如下:
怎么理解呢,還是先回顧單個時間步 的輸出 的計算公式:
上述公式最后一步和推理階段循環表示公式中各個元素的對應關系是:
對應論文中的圖示:
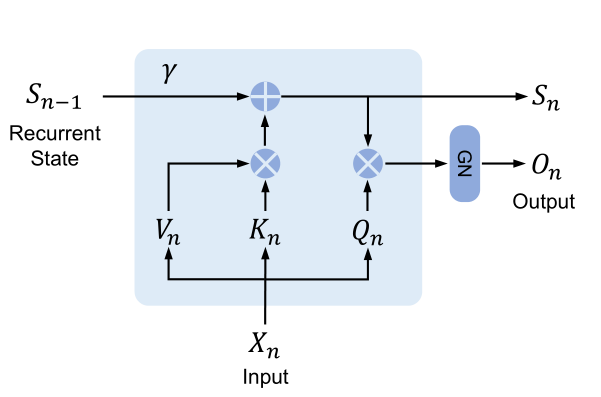
圖中的 表示 GroupNorm。
可以看到在推理階段,RetNet 在計算當前時間步 的輸出 只依賴于上一個時間步產出的狀態矩陣 。
其實就是把計算順序改了一下,先計算的 和 的相乘然后一直累加到狀態矩陣 上,最后再和 相乘。
而不是像 Transformer 架構那樣,每個時間步的計算要先算 和前面所有時間步的 相乘得到 attention 權值再和 相乘求和,這樣就需要一直保留歷史的 和 。
Gated Multi-Scale Retention
然后 RetNet 每一層中的 Retention 子模塊其實也是分了 個頭,每個頭用不同的 參數,同時每個頭都采用不同的 常量,這也是 ?Multi-Scale Retention 名稱的來由。
則對輸入 , MSR 層的輸出是:
其中, , 是激活函數用來生成門控閾值,還有由于每個頭均采用不同的 ,所以每個頭的輸出要單獨做 normalize 之后再 concat。
編輯:黃飛
?
 電子發燒友App
電子發燒友App





















評論