一種多類(lèi)原型模糊聚類(lèi)的初始化方法

模糊聚類(lèi)是非監(jiān)督模式分類(lèi)的一個(gè)重要分支，在模式識(shí)別和圖像處理中已經(jīng)得到了廣泛的應(yīng)用.但現(xiàn)有模糊聚類(lèi)算法大都需要聚類(lèi)數(shù)的先驗(yàn)知識(shí)，而且對(duì)初始化極為敏感，從而限制了它們的實(shí)際應(yīng)用.此外對(duì)于多類(lèi)原型樣本集的聚類(lèi)分析，還需要事先已知原型的類(lèi)型及相應(yīng)數(shù)目.為了克服這些限制，本文提出一種聚類(lèi)原型先驗(yàn)知識(shí)的獲取方法，并用來(lái)初始化多類(lèi)原型模糊聚類(lèi)，取得了較好的效果.
　　關(guān)鍵詞:模糊聚類(lèi)；數(shù)學(xué)形態(tài)學(xué)；細(xì)化；曲線擬合

An Initialization Method for Multi-Type Prototype Fuzzy Clustering

GAO Xin-bao,XUE Zhong,LI Jie,XIE Wei-xin
(School of Electronics Engineering,Xidian University,Xi'an 710071,China)

　　Abstract:Fuzzy clustering is an important branch of unsupervised classification,and has been widely used in pattern recognition and image processing.However,most of exiting fuzzy clustering algorithms are sensitive to initialization,and strongly depend on the number of clusters,which limits their applications.Moreover,it also needs to know the type and number of prototypes in advance in multi-type prototype fuzzy clustering.To overcome these limitation,a method for acquiring a priori knowledge about clustering prototype is proposed in this paper,which obtains better performance in initializing multi-type prototype fuzzy clustering.
　　Key words:fuzzy clustering;mathematical morphology;thinning;curve fitting

一、引　　言
　　聚類(lèi)分析是非監(jiān)督模式分類(lèi)的一個(gè)分支，其基本任務(wù)是把特征空間中一個(gè)未標(biāo)記的模式樣本集按照某種相似性準(zhǔn)則劃分到若干個(gè)子集中，使相似的樣本盡量歸為一類(lèi).傳統(tǒng)的聚類(lèi)分析是基于硬劃分的，每個(gè)樣本屬于且只屬于某一類(lèi).1973年Dunn［1］引入模糊集理論，定義了基于目標(biāo)函數(shù)J2(U,v)的模糊c-均值聚類(lèi)算法.后來(lái)，Bezdek［2］又推廣到了一個(gè)目標(biāo)函數(shù)的無(wú)限族，此后模糊c-均值聚類(lèi)算法成為研究的主流.在模糊聚類(lèi)中，樣本不再僅屬于某一類(lèi)，而是以不同的程度分屬于每一類(lèi)，表達(dá)出了樣本間的相近信息及事物在性態(tài)和類(lèi)屬方面的中介性，從而更符合人的分類(lèi)方式.
　　隨著模糊c-均值算法理論和應(yīng)用的發(fā)展［3］，為檢測(cè)橢球狀分布以外的模式子集，該算法被逐步推廣到模糊c-線［4］、模糊c-殼［5］以及模糊c-二次曲線［6］等新型算法.新算法把聚類(lèi)原型從點(diǎn)擴(kuò)展到了線、面、殼等幾何結(jié)構(gòu)，把模糊聚類(lèi)的應(yīng)用范圍從簡(jiǎn)單的模式分類(lèi)拓寬到基元檢測(cè)、曲線擬合等眾多領(lǐng)域.作為上述算法的集成和統(tǒng)一，最近提出了一種多類(lèi)原型模糊聚類(lèi)算法［7］，該算法中聚類(lèi)原型不再是單一的形式，而是多類(lèi)原型的混合，因此可以同時(shí)檢測(cè)呈不同幾何結(jié)構(gòu)分布的樣本子集.
　　然而上述各類(lèi)算法大都依賴于聚類(lèi)原型和聚類(lèi)數(shù)的先驗(yàn)知識(shí)，即必須事先已知樣本子集分布的幾何結(jié)構(gòu)及類(lèi)別數(shù)，這限制了它們?cè)谏a(chǎn)自動(dòng)化中的應(yīng)用.此外，這些算法均采用局部搜索技術(shù)，因此對(duì)初始化極為敏感，即使在聚類(lèi)原型和聚類(lèi)數(shù)給定的情況下，如果種子點(diǎn)選擇不當(dāng)，也很容易陷于局部極值點(diǎn)，得不到最佳分類(lèi).
　　針對(duì)以上限制及缺點(diǎn)，本文提出了一種結(jié)合數(shù)學(xué)形態(tài)學(xué)、圖像描述及曲線擬合等技術(shù)的初始化方法.本方法不僅可以估計(jì)各類(lèi)原型的位置，而且能夠自動(dòng)獲取原型的結(jié)構(gòu)參數(shù)及數(shù)目，從而使聚類(lèi)分析成為真正的機(jī)器自動(dòng)學(xué)習(xí)算法.
　　以下，第二部分簡(jiǎn)要介紹多類(lèi)原型的模糊聚類(lèi)分析，第三部分引入幾個(gè)數(shù)學(xué)形態(tài)學(xué)算子，第四部分給出聚類(lèi)原型參數(shù)的自動(dòng)獲取方法，第五部分為實(shí)驗(yàn)結(jié)果及討論，最后是結(jié)論及后續(xù)工作.

二、多類(lèi)原型的模糊聚類(lèi)
　　多類(lèi)原型的模糊聚類(lèi)［7］是傳統(tǒng)模糊聚類(lèi)的集成和統(tǒng)一，在這種分析方法中聚類(lèi)原型不再是單一的形式，而是呈現(xiàn)多樣化.它不僅能完成現(xiàn)有各種聚類(lèi)算法的功能，即檢測(cè)單一模式樣本子集，而且可以用來(lái)分析呈多種幾何結(jié)構(gòu)分布的特征集.除模式分類(lèi)外，該算法還能實(shí)現(xiàn)基元檢測(cè)、物體識(shí)別等多種功能.
　　設(shè)x為Rp中的一個(gè)子集x={x1,x2,…,xn}Rp,xk=(xk1，xk2，…，xkp)∈Rp稱為特征矢量或模式矢量，xkj為觀測(cè)樣本xk的第j個(gè)特征.設(shè)Vcn是所有c×n階的矩陣集合，c為［2,n)區(qū)間內(nèi)的整數(shù)，則x的模糊c-劃分空間為：

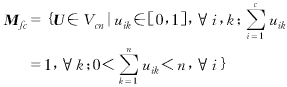　(1)

其中U矩陣的元素uik表示第k個(gè)樣本xk屬于第i個(gè)聚類(lèi)的程度.設(shè)B={β1，β2，…,βc}為聚類(lèi)原型集，其中為第i個(gè)模糊子集的模式原型，則多類(lèi)原型的模糊劃分可以通過(guò)極小化如下的目標(biāo)函數(shù)而得到：

　(2)

式中，m為模糊指數(shù)，m越大分類(lèi)的模糊度越大，當(dāng)時(shí)，退化為硬聚類(lèi)算法；D(xk,βi)為樣本xk與第i個(gè)原型βi的相似性測(cè)度，當(dāng)c個(gè)原型βi(i=1,…,c)均為RP空間中的點(diǎn)、線或殼時(shí)，該算法分別退化為模糊c-均值、模糊c-線或模糊c-殼聚類(lèi).
　　Jm(U,B)通過(guò)U與B的迭代沿著一子序列而逐漸收斂到初始B(0)附近的極值點(diǎn)或鞍點(diǎn)［8］，由于Jm(U,B)是一個(gè)多峰的復(fù)雜函數(shù)，因此原型B的初始化就變得尤為重要，一個(gè)隨機(jī)的初始化，可能導(dǎo)致分類(lèi)的錯(cuò)誤.而如果初始化B(0)落到包含有最佳B*的收斂子序列中，則能保證Jm(U,B)最終收斂到全局最優(yōu)點(diǎn).此外，對(duì)于多類(lèi)原型的模糊聚類(lèi)算法必須事先已知原型的類(lèi)型及相應(yīng)的數(shù)目，否則將無(wú)法得到正確的聚類(lèi)結(jié)果.因此需要有效的初始化方法來(lái)提供有關(guān)聚類(lèi)原型的信息.

三、數(shù)學(xué)形態(tài)學(xué)的基本算子
　　為了設(shè)計(jì)一種多類(lèi)原型模糊聚類(lèi)的初始化方法，需要引入數(shù)學(xué)形態(tài)學(xué)中的幾個(gè)基本算子和基本操作.首先介紹幾個(gè)習(xí)慣表示符，令帶有下劃線的大寫(xiě)字母“A，B，…”表示N維離散空間中的二值點(diǎn)集；集合中的點(diǎn)定義為N維整數(shù)坐標(biāo)的矢量，用相應(yīng)的大寫(xiě)字母表示為“A,B，…”；并用帶有下標(biāo)的小寫(xiě)字母“a1，a2,…,aN”表示矢量A的各個(gè)分量，比如：A=(a1,a2,…,an,…,aN)T.
　　1.膨脹與腐蝕算子
　　設(shè)X，S，…ZN，且元素X=(x1,x2,…,xn,…,xN)T和S=(s1,s2,…,sn,…,sN)T都是具有離散坐標(biāo)的N元組，如果用

(X)s={T∈ZN|T=X+S,X∈X}　(3)

表示點(diǎn)集X平移S，則X被S膨脹可基于Minkowski加法而定義為：

　(4)

同樣，基于Minkowski減法可以定義S對(duì)X的腐蝕操作

　(5)

其中S稱為結(jié)構(gòu)元素.
　　2.開(kāi)、閉運(yùn)算
　　在實(shí)際中，膨脹、腐蝕算子很少單獨(dú)使用，而是相互結(jié)合成對(duì)使用，這就是常見(jiàn)的數(shù)學(xué)形態(tài)學(xué)中的開(kāi)運(yùn)算和閉運(yùn)算.設(shè)我們用XS表示集合X相對(duì)于S的結(jié)構(gòu)開(kāi)，則開(kāi)運(yùn)算Xs為集合X相對(duì)于結(jié)構(gòu)元素S先腐蝕后膨脹的結(jié)果，即有

　(6)

開(kāi)運(yùn)算具有平滑功能，它能消除集合X幾何結(jié)構(gòu)中孤立的小點(diǎn)，毛刺和小橋，使XS變成一個(gè)邊緣相對(duì)光滑、簡(jiǎn)單的結(jié)構(gòu).
　　由對(duì)偶性，集合X相對(duì)于S的結(jié)構(gòu)閉XS，即為先膨脹后腐蝕的結(jié)果，有

　(7)

閉運(yùn)算也具有過(guò)濾功能，能填平集合X幾何結(jié)構(gòu)中的孔洞、彌補(bǔ)小裂縫.
　　實(shí)驗(yàn)中，我們發(fā)現(xiàn)對(duì)集合X先相對(duì)于S作膨脹操作，然后再作開(kāi)運(yùn)算就不再改變其大體結(jié)構(gòu).因此下一節(jié)中我們將構(gòu)造開(kāi)、閉運(yùn)算的鏈?zhǔn)讲僮鱽?lái)刪除待聚類(lèi)數(shù)據(jù)集中的細(xì)節(jié)，而保留模式子集結(jié)構(gòu)的總體形狀，以便獲取聚類(lèi)原型的有關(guān)信息.

四、聚類(lèi)原型及聚類(lèi)數(shù)的自動(dòng)獲取
　　在呈多類(lèi)原型分布的模式集中，特征矢量在特征空間中的分布可用如下模型描述：

xk=βi+εi，xk∈ci,εi∈N(0,σi)　(8)

其中xk為特征矢量；ci為矢量xk最貼近的模式子集，即有uik=maxcj=1uij;βi為模式子集或聚類(lèi)ci的原型；N(0,σi)表示高斯分布.也就是說(shuō)，貼近于同一個(gè)聚類(lèi)的矢量按照正態(tài)分布模式聚集在原型的附近，σi反映了其聚散程度.由高斯分布的特點(diǎn)可知，聚類(lèi)ci中的樣本絕大多數(shù)都散布在鄰域Δ內(nèi)，因此定義聚類(lèi)ci的厚度為3σi.基于樣本分布的這些形態(tài)特征，可以借助形態(tài)處理來(lái)提取聚類(lèi)原型信息.
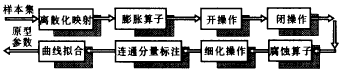
　　一個(gè)聚類(lèi)原型信息自動(dòng)獲取的流程可由圖1所示的框圖來(lái)表示：