幾乎周期時變MA系統的辨識
本文利用循環統計量討論幾乎周期時變滑動平均(APTV-MA)系統的辨識問題.提出了基于奇數階時變累量的參數估計的法方程方法,并導出了基于時變累量和循環累量的系統模型定階方法.仿真實驗說明了本文所提方法的性能.
關鍵詞:循環統計量;幾乎周期時變MA系統;法方程;系統辨識
Identification of Almost Periodic Time-Varying MA Systems
LI Hong-wei
(Department of Mathermatics and Physics,China University of Geoscience,Wuhan 430074,China)
YUAN Bao-zong
(Institute of Information Science,Northern Jiaotong University,Beijng 100044,China)
Abstract:This paper addresses the problem of identification of almost periodic time-varying moving average (APTV-MA) systems using cyclic statistics.The normal equation approaches based on odd order time-varying cumulants are presented for parameters estimation.Model order detemination procedures based on time-varying and cyclic cumulants are also derived.Simulations are performed to illustrate performance of the presented methods.
Key words:cyclic statistics;almost periodic time-varying MA system;normal equation;identification of system
一、引 言
考慮q階幾乎周期時變滑動平均(APTV-MA)信號模型
![]() (1)
(1)
并且,假設下列假定成立.
假定1 激勵噪聲?(t)是零均值獨立同分布的,且存在一個奇數k(![]() 3),使得其k階累量γk?滿足0<|γk∈|<+∞.
3),使得其k階累量γk?滿足0<|γk∈|<+∞.
假定2 對于每一個固定的n,有限沖激響應序列h(t,n)是關于t的幾乎周期實序列(可以是非最小相位的),并且,h(0,0)=1;h(t,0)≠0,h(t,q)≠0,![]() t.
t.
在實際應用中,信號x(t)是在噪聲中被觀測的:
y(t)=x(t)+v(t),t=0,1,…,T-1 (2)
其中,加性噪聲v(t)滿足
假定3 v(t)是一個與∈(t)獨立的功率譜未知的零均值高斯(有色)過程(可以是非平穩的).
在模型(2)下,y(t)是非平穩的,原有的討論時不變MA系統的辨識方法不能直接應用.易證y(t)是循環平穩的.因此,我們的目的是根據觀測值{y(t),t=0,1,…,T-1}利用循環統計量來估計![]()
上述問題可以看作時不變MA系統在幾乎周期時變情形的推廣.這一類問題在通訊,水文氣象等領域具有廣泛的應用[5,11,14].在高斯信號情形,文獻[15]提出了基于二階統計量的近似最大似然技術估計信號參數.相關問題的討論可見文獻[8]和[13].最近[5],Dandawate和Giannakis對于幾乎周期時變MA信號進行了較深入的研究,他們利用高階循環統計量來辨識APTV-MA系統,提出了模型參數估計的線性和非線性算法以及一種統計的定階方法.
眾所周知,對于時不變MA系統,基于高階累量的參數估計方法可分為閉式解,法方程和非線性最優化解三大類[12].由于不涉及極值問題求解,前二種線性方法尤其令人重視[7,17].但是到目前為止,對于幾乎周期時變MA系統的辨識,這兩種方法的研究還較小.本文討論利用循環統計量辨識APTV-MA系統的新方法,提出了參數估計的法方程方法和基于時變累量和循環累量的時域定階方法.
二、參數估計方法
在本節先假定幾乎周期時變MA系統的階q已知,推導APTV-MA信號參數的法方程.
實信號z(t)的k階時變的和循環的累量分別定義[3,5]為
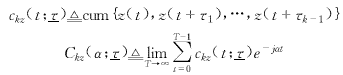
其中,τ=(τ1,…,τk-1).有關循環統計量的詳細定義和記號參見文獻[3].
當k![]() 3時,由假定3和累量性質有ckx(t;τ)=cky(t;τ).即觀測信號y(t)與無加性噪聲污染的輸出信號x(t)具有相同的時變累量,因此,在基于高階時變和循環累量的分析中不必考慮加性高斯噪聲的影響.
3時,由假定3和累量性質有ckx(t;τ)=cky(t;τ).即觀測信號y(t)與無加性噪聲污染的輸出信號x(t)具有相同的時變累量,因此,在基于高階時變和循環累量的分析中不必考慮加性高斯噪聲的影響.
由累量性質可知,滿足模型(1)和假定1~2的APTV-MA信號x(t)的k(>3)階時變累量為
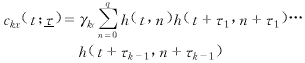 (3)
(3)
它是時不變MA系統的BBR公式[1]在APTV-MA情形的推廣.
令τ1=τ2=…=τk-2=q,則由式(3)得到
ckx(t;q,…,q,τk-1)=γk∈h(t,0)hk-2(t+q,q).h(t+τk-1,τk-1) (4)
利用上式不難得到
ckx(t-i;q,…,q,i)=γk∈h(t-i,0)hk-2(t-i+q,q)h(t,i)
ckx(t-i;q,…,q,q)=γk∈h(t-i,0)hk-1(t-i+q,q)
ckx(t-i;q,…,q,0)=γk∈h2(t-i,0)hk-2(t-i+q,q)
由上述得到
γk∈hk(t;i)=ckkx(t-i;q,…,q,i)/[ck-2kx(t-i;q,…,q,q).ckx(t-i;q,…,q,0)] (5)
由上式(t=i=0)和假定2(h(0,0)=1)可知,
γk∈=ck-1kx(0;q,…,q,0)/ck-2kx(0;q,…,q,q) (6)
當k為奇數時,
h(t,i)=ckx(t-i;q,…,q,i)/{γ1/kkx[ck-2kx(t-i;q,…,q,q)
.ckx(t-i;q,…,q,0)]1/k} (7)
因此,當k為奇數時,由式(6)和式(7)可以獲得沖激響應序列h(t,i).當k為偶數時,由式(6)和式(7)只能得到h(t,i)的幅值,而無法判定其符號.相應于時不變情形的結果見文獻[6].
特別地,當k=3時,式(6)和式(7)成為
γ3∈=c33x(0;q,0)/c3x(0;q,q)
h(t,i)=c3x(t-i;q,i)/{γ1/33∈[c3x(t-i;q,q)
.c3x(t-i;q,0)]1/3}
文獻[5]也得到了上式,式(6)和式(7)將文獻[5]的結果推廣到任意奇數階累量情形.
雖然在奇數階情形可以利用式(6)和式(7)來估計h(t,i),但是與時不變情形類似,這種方法將產生較大的估計誤差,考慮下面的法方程方法.
在式(3)中,令τ1=i,τ2=…=τk-1=0,得到
![]() (8)
(8)
式(8)可以變換為
![]() (9)
(9)
記
B1![]() (ckx(t+q;-q,0,…,0),ckx(t+q-1;
(ckx(t+q;-q,0,…,0),ckx(t+q-1;
-q+1,0,…,0),…,ckx(t-q;q,0,…,0))T.
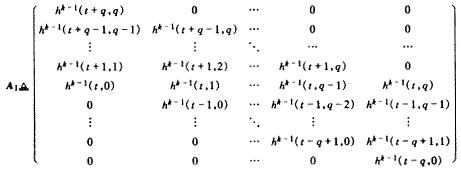
H1![]() (γk∈h(t,0),γk∈h(t,1),…,γk∈h(t,q-1),γk∈h(t,q))T.
(γk∈h(t,0),γk∈h(t,1),…,γk∈h(t,q-1),γk∈h(t,q))T.
在式(9)中令i=-q,-q+1,…,-1,0,1,…,q,可得
A1H1=B1 (10)
將式(6)和式(7)代入A1,求解超定線性方程組(10),可以得到γk∈和h(t,n).
方程(10)是本文得到的基于時變累量的APTV-MA系統參數的線性法方程.在A1中,考慮其前q+1行構成的三角陣,由假定2可知這個三角陣的對角線元素用式(6)和式(7)中的時變累量代入均不為零,三角陣是滿秩的,故秩A1=q+1.因此,易得如下的唯一識別定理.
定理1 在模型(1)之下,假定信號的k階累量已知,則由方程(10)確定的H1的解是唯一的.
在實際的估計計算中,為求解線性方程組(10),需要將A1和B1中的元素用其估計值代替,有關循環統計量的估計將在第四節中討論.
由式(8)得到另一類法方程,記
A2![]()
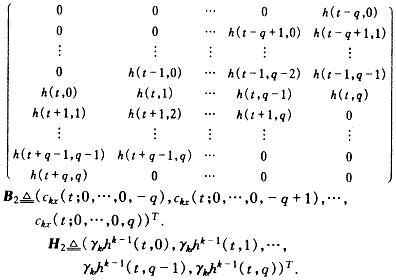
在式(8)中令i=-q,-q+1,…,-1,0,1,…,q,可得
A2H2=B2 (11)
將式(6)和式(7)代入A2,求解超定線性方程組(11),得到γk∈和h(t,n)的幅值,其符號可由式(6)和式(7)確定.
方程(11)是得到的基于時變累量的另一類線性法方程,類似于式(10)的討論可知,秩A2=q+1.因此,可得如下的唯一識別定理.
定理2 在模型(1)之下,假定信號的k階累量已知,則由方程(11)確定的H2的解是唯一的.
三、APTV-MA模型定價
在上節的討論中,假定APTV-MA系統的階q是已知的,在許多實際問題中,模型的階是未知的.因此,本節計論APTV-MA系統階次的確定問題.
根據式(8),有
![]() (12)
(12)
以上兩式指出,APTV-MA的階數q是使ckx(t;i,0,…,0)≠0滿足的最大正整數imax.因此,定階問題轉化為判定時變累量是否為零的問題.與時不變MA情形一樣,在估計計算中,對于一組在噪聲中觀測到的有限長度數據,由樣本估計檢驗累量為零成立與否的閾值是難以確定的.為了解決這個問題,文獻[16]在討論時不變MA系統定價問題時,提出了一種新穎的時域定階方法,該方法易于實現,且具有較好的數值魯棒性.受該方法的啟發,討論APTV-MA信號的定階.
1.基于時變累量的模型定階
利用信號x(t)的k階時變累量構造矩陣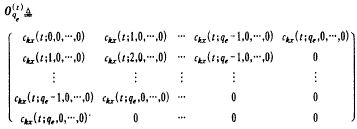 (13)
(13)
其中,qe(>q)是模型階次的上界(它在實際應用中是容易取到的),由式(12)可知,秩O(t)qe=q+1.因此,模型的階確定轉化為矩陣(13)的秩的確定.
在實際應用中,式(13)中的元素用樣本估計代替,用奇異值分解[2]求O(t)qe的有效秩,即可確定APTV-MA的階數.
由式(13),矩陣O(t)qe的有效秩的確定實際上等價于驗證
ci+1kx(t;i,0,…,0)≠0,i>0
使得上式成立的最大正整數imax即是模型的階數q.因此,基于時變累量的APTV-MA的定階方法如下,將ckx(t;i,0,…,0)用其樣本估計![]() kx(t;i,0,…,0)代替,選擇使得
kx(t;i,0,…,0)代替,選擇使得
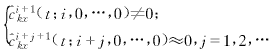 (14)
(14)
成立的最大正整數imax作為階數q的估計.
2.基于循環累量的模型定價
上一小節討論的是基于t時刻時變累量的定階方法,下面討論基于循環累量的定階方法,由時變累量和循環累量的關系[3],有
![]() t,ckx(t;τ)=0
t,ckx(t;τ)=0![]()
![]() α,Ckx(α;τ)=0
α,Ckx(α;τ)=0
由式(12),有
至少存在一個α0,使得Ckx(α0;q,0,…,q)≠0;
![]() α,Ckx(α;i,0,…,0)=0,i>q (15)
α,Ckx(α;i,0,…,0)=0,i>q (15)
模型定階轉化為找使上兩式成立的最大正整數imax.根據上節的討論,對于某一α0的qe>q,構造矩陣O(c)qe(見式(16)).易知秩O(c)qe=q+1,即模型定階轉化為判定矩陣O(c)qe的秩.
在實際應用中,盡管可以用奇異值分解來判定O(c)qe的有效秩,但必須先找α0,這在應用中是相當麻煩的.然而,類似上一小節的討論,對于某一α0,只須找到使Ci+1kx(α0;i,0,…,0)≠0成立的最大的正整數imax作為模型階數q的估計.這等價于選擇使得[supα|Ckx(α;i,0,…,0)|]i+1≠0成立的最大的正整數imax作為模型階數q的估計.
O(c)qe![]()
 (16)
(16)
因此,基于循環累量的APTV-MA的定階方法如下,將Ckx(α;i,0,…,0)用其樣本估計代替,選擇使得
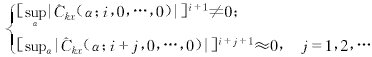 (17)
(17)
成立的最大正整數imax作為階數q的估計.
四、樣本估計和收斂性討論
在上兩節中,提出了APTV-MA系統的定階方法和參數估計的法方程方法,它們是基于時變的和循環的累量進行的.在實際的估計計算中,這些統計量只能由有限長度的樣本(觀測數據)![]() 進行估計而得到.
進行估計而得到.
對于滿足模型(2)和假定1-3的APTV-MA信號y(t),由循環累量的定義可知,當k![]() 3時,Cky(α;τ)=Ckx(α;τ).若要估計ckx(t;τ)和Ckx(α;τ),只須估計cky(t;τ)和Cky(α;τ).
3時,Cky(α;τ)=Ckx(α;τ).若要估計ckx(t;τ)和Ckx(α;τ),只須估計cky(t;τ)和Cky(α;τ).
對于一般的k階情形,cky(t;τ)和Cky(α;τ)的強相容估計可以按照文獻[9]的方法得到.
對于k=1,有c1y(t)=C1y(α)=0.
對于k=3,y(t)的三階循環矩和時變矩估計分別為
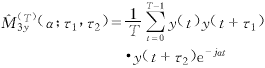 (18)
(18)![]() (19)
(19)
其中,![]() ,y(t)的三階時變累量和循環累量估計分別為
,y(t)的三階時變累量和循環累量估計分別為
![]() (20)
(20)![]() (T)3y(α;τ1,τ2)=
(T)3y(α;τ1,τ2)=![]() (T)3y(α;τ1,τ2) (21)
(T)3y(α;τ1,τ2) (21)
在上述估計中,循環矩估計![]() (T)3y(α;τ)是一個關鍵的估計量,時變的和循環的累量估計都是由它獲得的.另外有一個量需要估計的是Am3y.關于它的估計,有兩種方法.一種是統計檢驗方法[4],另一種是基于DFT的直接檢驗方法[10].
(T)3y(α;τ)是一個關鍵的估計量,時變的和循環的累量估計都是由它獲得的.另外有一個量需要估計的是Am3y.關于它的估計,有兩種方法.一種是統計檢驗方法[4],另一種是基于DFT的直接檢驗方法[10].
在模型(2)的假定之下,由文獻[9]的定理,可知上述關于時變累量和循環累量的估計都是其真值的強相容估計.由前兩節的參數唯一識別定理和矩陣擾動分析理論可知,上兩節提出的參數和階數估計均是強收斂的.
五、仿真實驗
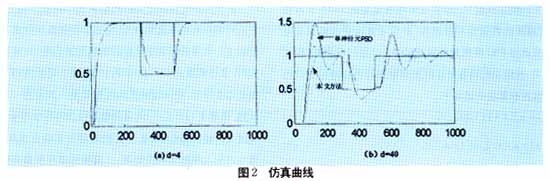
為了檢驗本文提出的基于時變和循環累量的模型定階方法和參數估計的法方程方法對APTV-MA信號的定階和參數估計的性能,進行了如下的仿真實驗.
例 驅動噪聲?(t)是零均值獨立的指數分布隨機數,并且,σ2?=1,γ3∈=2.加性噪聲v(t)取為零均值AR(2)高斯過程:
v(t)-1.6v(t-1)+0.68v(t-2)=e(t) (22)
APTV沖激響應序列h(t,n)取為關于t的周期為2的實序列:
t為偶數時:h(t,0)=1,h(t,1)=0.2,t(t,2)=-0.75
t為奇數時:h(t,0)=0.6,h(t,1)=-0.65,t(t,2)=1.2
即無噪聲污染的信號x(t)是一個周期為2的時變MA(2)過程.當t為偶數時,x(t)=∈(t)+0.2∈(t-1)-0.75∈(t-2).它是最小相位的,其零點為0.7713和-0.9713.當t為奇數時,x(t)=0.6∈(t)-0.65∈(t-1)+1.2∈(t-2).它是非最小相位的,其零點為0.5417±1.3064j.信噪比定義為SNR=10log10(σ2?/σ2v).
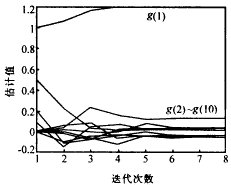
在實驗中,信噪比取為0dB,觀測數據由上述參數和式(2)產生.數據長度取為8192,Monte Carlo運行次數為100.基于三階時變累量和法方程方法(式(10))的參數估計的統計結果見表1.基于t=0時刻的三階時變累量的定階統計結果見表2.基于三階循環累量的定階統計結果見表3.
表1 基于三階時變累量的參數估計的統計結果
| 待估參數 | γ3? | h(0,1) | h(0,2) | h(1,0) | h(1,1) | h(1,2) |
| 真值 | 2.00000 | 0.20000 | -0.75000 | 0.60000 | -0.65000 | 1.20000 |
| 估計均值 | 2.02758 | 0.26036 | -0.75511 | 0.61655 | -0.59606 | 1.16906 |
| 標準偏差 | 0.29703 | 0.09312 | 0.11403 | 0.12365 | 0.12205 | 0.18681 |
|
表2 基于三階時變累量的定階統計結果 |
| i值 | ||||
| 均值 | 標準偏差 | 均值 | 標準偏差 | |
| i=1 | -0.45716 | 0.17114 | 0.23829 | 0.16242 |
| i=2* | 0.88060 | 0.28343 | 0.90109 | 0.83031 |
| i=3 | -0.01843 | 0.14205 | 0.00112 | 0.00243 |
| i=4 | 0.02757 | 0.20303 | 0.00085 | 0.00387 |
| i=5 | 0.04614 | 0.15643 | 0.00050 | 0.00270 |
| i=6 | 0.00925 | 0.18165 | 0.00006 | 0.00055 |
| i=7 | 0.01157 | 0.12909 | 0.00001 | 0.00003 |
| i=8 | 0.01862 | 0.21002 | 0.00004 | 0.00084 |
| i=9 | 0.01646 | 0.14416 | 0.00000 | 0.00002 |
| i=10 | 0.01380 | 0.17514 | 0.00000 | 0.00002 |
|
表3 基于三階循環累量的定階統計結果 |
| i值 | supα| |
supα| | ||
| 均值 | 標準偏差 | 均值 | 標準偏差 | |
| i=1 | 0.74568 | 0.11763 | 0.56988 | 0.18373 |
| i=2* | 1.17688 | 0.16014 | 1.72152 | 0.70514 |
| i=3 | 0.47164 | 0.05893 | 0.05441 | 0.03061 |
| i=4 | 0.44282 | 0.05312 | 0.01968 | 0.01309 |
| i=5 | 0.40810 | 0.04865 | 0.00577 | 0.00514 |
| i=6 | 0.39960 | 0.04397 | 0.00211 | 0.00184 |
| i=7 | 0.37370 | 0.04522 | 0.00058 | 0.00074 |
| i=8 | 0.38182 | 0.04109 | 0.00026 | 0.00031 |
| i=9 | 0.36517 | 0.03844 | 0.00007 | 0.00009 |
| i=10 | 0.38063 | 0.04190 | 0.00005 | 0.00009 |
| 表1說明參數估計的法方程方法具有較好的估計勻值和較小的標準偏差.特別要指出的是,例題中的系統不僅是周期時變的,而且是非最小相位的. 表2~3說明基于時變和循環累量的定階方法(與直接判定統計量相比較)具有很好的數值穩定性,且每次運算都能給出準確的階數估計(q=imax=2). 在實驗中,盡管信噪比較低,但是所用的數據長度較大(與傳統的二階統計量方法和累量方法比較),這是因為循環統計量具有較大的估計方差. 六、結束語 |
 電子發燒友App
電子發燒友App




















評論