本文將混沌引入到蟻群算法(Ant Colony Optimization，ACO)當中，以形成混沌蟻群算法(Chaos Ant Colony Optimization，CACO)，從而提高了對于BP神經(jīng)網(wǎng)絡(luò)的優(yōu)化效率和精度，解決了上述問題；同時，也在對異步電機直接轉(zhuǎn)矩控制(DTC)轉(zhuǎn)速辨識的仿真試驗中，實現(xiàn)了對電機轉(zhuǎn)速的準確辨識。基于BP神經(jīng)網(wǎng)絡(luò)模型的速度辨識方法得到了廣泛研究，但其仍存在收斂速度慢、易陷入局部極小值等問題，因此，對神經(jīng)網(wǎng)絡(luò)的優(yōu)化一直是當前的研究熱點。

1 BP神經(jīng)網(wǎng)絡(luò)的缺點

BP神經(jīng)網(wǎng)絡(luò)是目前控制領(lǐng)域中應(yīng)用廣泛的一種神經(jīng)網(wǎng)絡(luò)模型，其學(xué)習(xí)過程由信息前向計算和誤差反向傳播過程組成。它采用梯度搜索技術(shù)，可使網(wǎng)絡(luò)的實際輸出值與期望輸出值的誤差均方值最小化。此外，該網(wǎng)絡(luò)還具有良好的非線性映射和泛化能力。BP神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)如圖1所示。



BP神經(jīng)網(wǎng)絡(luò)的數(shù)學(xué)模型為：



其中，x_j為輸入層節(jié)點輸出，y_i為隱含層節(jié)點輸出，O₁為輸出層輸出。輸入層節(jié)點與隱含層節(jié)點間的網(wǎng)絡(luò)連接權(quán)值為ω_ij；隱含層節(jié)點與輸出層節(jié)點間的網(wǎng)絡(luò)連接權(quán)值為T_li；輸出層節(jié)點l的期望輸出為t₁。f(net)為傳遞函數(shù)。為此，其網(wǎng)絡(luò)連接權(quán)值的調(diào)整公式如下：



其中，η為學(xué)習(xí)速率(η>0)；k為訓(xùn)練次數(shù)，α為平滑因子(0<α<1)，為隱層節(jié)點誤差。

2 BP神經(jīng)網(wǎng)絡(luò)的混沌蟻群優(yōu)化過程

2.1?基本蟻群算法

ACO的基本思路是：在算法的初始時刻，將一定數(shù)量的螞蟻隨機放在給定的N座城市上，并設(shè)此時各路徑上的信息素相等。螞蟻在運動過程中根據(jù)各條路徑上的信息素量獨立選擇下一城市。螞蟻系統(tǒng)使用的轉(zhuǎn)移規(guī)則是根據(jù)螞蟻在兩個城市之間的轉(zhuǎn)移概率來進行路徑選擇。在完成一次循環(huán)后，螞蟻在路徑上釋放一定量的信息素。完成一次循環(huán)所走過的路徑就是問題的一個解，當所有螞蟻都完成循環(huán)后，即可得到最優(yōu)解。

蟻群算法的基本公式如下：



2.2?混沌蟻群算法

混沌蟻群算法(CACO)是受到自然界螞蟻走行的混沌特點和整個種群的自組織特點的啟發(fā)。它利用混沌的遍歷性和隨機性等特點來將混沌擾動算子引入蟻群算法，并將帶有混沌特征的初始化變量線性映射到變量取值區(qū)間。該方法兼顧了混沌動態(tài)搜索和智能搜索的特點，可有效地避免搜索過程中陷入局部最優(yōu)，從而達到提高算法速度和全局尋優(yōu)的能力。

(1)混沌初始化

設(shè)τ_ij(t)為t時刻路徑上的信息濃度，利用混沌運動的遍歷性進行混沌初始化。混沌變量選擇典型的混沌系統(tǒng)Logistic映射迭代公式如下：



式中，μ為控制參數(shù)，當μ=4時，Logistic完全處于混沌狀態(tài)，此時系統(tǒng)在[0，1]之間具有遍歷性。如果利用全排列理論將每個混沌變量對應(yīng)于一條路徑，也就是為每條路段上的信息素濃度根據(jù)混沌量給定初始值τ_ij(0)，就可以有效地解決基本蟻群算法收斂速度慢的問題。

(2)引入混沌擾動量

在蟻群算法中，如果螞蟻后從點i至某一點j，則在路徑ij上留下信息素τ_ij(t)。螞蟻k在走完任意一路徑以后，將按式(5)更新該路徑上的信息素。可以看出，此更新方法在加快尋優(yōu)的同時，卻容易陷入局部最優(yōu)解。因此，在此處引入混沌擾動量來調(diào)整信息素，以使其避免陷入局部最優(yōu)極值區(qū)間。改進后的式子為：



其中，X_ij為混沌擾動量，可采用典型混沌系統(tǒng)Logistic映射得到，q為相關(guān)系數(shù)。

2.3? 混沌蟻群算法的實現(xiàn)步驟

實現(xiàn)混沌蟻群算法的具體步驟如下：

Step1：初始化BP網(wǎng)絡(luò)結(jié)構(gòu)，設(shè)定網(wǎng)絡(luò)的輸入層、隱含層、輸出層的神經(jīng)元個數(shù)；

Step2：混沌初始化信息素濃度、個體最優(yōu)和全局最優(yōu)；

Step3：用公式(4)計算每只螞蟻的轉(zhuǎn)移概率；

Step4：根據(jù)每只螞蟻的轉(zhuǎn)移概率得出本次最優(yōu)路徑并最優(yōu)值比較，若更優(yōu)，則更新最優(yōu)值；

Step5：將每只螞蟻的最優(yōu)值與整個蟻群的最優(yōu)值相比較，若更優(yōu)，則其將成為整個蟻群新的最優(yōu)值；

Step6：更新并按公式(9)修改路徑ij上的信息素濃度；

Step7：比較次數(shù)是否達到預(yù)設(shè)的精度，若滿足預(yù)設(shè)精度，則最后一次迭代的全局最優(yōu)值中每一維的權(quán)值和閾值就是所求的；否則返回step3，算法繼續(xù)迭代，直至滿足條件為止。

3?基于DTC的系統(tǒng)仿真

3.1?直接轉(zhuǎn)矩控制系統(tǒng)結(jié)構(gòu)

直接轉(zhuǎn)矩控制(DTC)系統(tǒng)的結(jié)構(gòu)原理如圖2所示。在α-β坐標系下，通過獲得定子電壓U_sα、U_sβ，定子電流I_sα、I_sβ及定子電流導(dǎo)數(shù)pI_sα、pI_sβ歸一化后，即可構(gòu)成神經(jīng)網(wǎng)絡(luò)的六個輸入，再經(jīng)過反歸一化，即可得到轉(zhuǎn)子轉(zhuǎn)速ω，從而構(gòu)建一個動態(tài)轉(zhuǎn)速估計器。

3.2?仿真實驗

在MATLAB／Simulink仿真環(huán)境下建立直接轉(zhuǎn)矩控制系統(tǒng)的仿真平臺時，系統(tǒng)采樣周期可設(shè)定為0.1 ms，異步感應(yīng)電動機的其它各參數(shù)為：額定功率P_N=15 kW，額定電壓V_N=380 V，額定頻率f_N=50 Hz，定子電阻R_s=0.435 Ω，轉(zhuǎn)子電阻R_r=0.816 Ω，定子電感L_s=0.002H，轉(zhuǎn)子電感L_r=0.002H，定轉(zhuǎn)子互感L_m=0.06931H，極對數(shù)p=2，轉(zhuǎn)動慣量J=0.0918 kg.m²。設(shè)定電機轉(zhuǎn)速ω=20 rad／s時，采取1000組數(shù)據(jù)作為訓(xùn)練樣本，5000組數(shù)據(jù)作為驗證樣本，最大訓(xùn)練次數(shù)設(shè)定為2000次，最小容許誤差設(shè)定為0.001。

學(xué)習(xí)網(wǎng)絡(luò)的隱含層節(jié)點個數(shù)經(jīng)多次訓(xùn)練后確定為k₁=11和k₂=6，設(shè)n為輸入節(jié)點個數(shù)。混沌變量個數(shù)m為神經(jīng)網(wǎng)絡(luò)所有權(quán)值、閾值的總和，m=156，蟻群種群數(shù)M=30，p=0.8，Q=50。其算法訓(xùn)練誤差比較如表1所列。



從表1可以看出，傳統(tǒng)的BP算法優(yōu)化神經(jīng)網(wǎng)絡(luò)的最小適應(yīng)度收斂十分緩慢，并且誤差較大。而混沌蟻群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)誤差更小，精度更高，其收斂性要遠遠優(yōu)于傳統(tǒng)的BP算法。

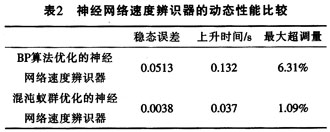
表2所列是由實驗仿真結(jié)果中分別提取出的神經(jīng)網(wǎng)絡(luò)速度辨識器的動態(tài)性能指標。可以看出，混沌蟻群優(yōu)化的神經(jīng)網(wǎng)絡(luò)較之傳統(tǒng)BP算法的動態(tài)性能有了很大改進。



4 結(jié)束語

本文構(gòu)造了一種基于混沌蟻群算法的BP神經(jīng)網(wǎng)絡(luò)模型，并將其應(yīng)用到直接轉(zhuǎn)矩控制系統(tǒng)中的轉(zhuǎn)速辨識器中，從而顯示出其辨識非線性函數(shù)的優(yōu)越性能以及速度快、精度高的特點。仿真結(jié)果表明，用混沌蟻群優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)速度辨識器是可行的，而且具有較強的速度跟蹤精度，可實現(xiàn)直接轉(zhuǎn)矩控制系統(tǒng)的無速度傳感器控制，而且系統(tǒng)具有良好的動、靜態(tài)性能。