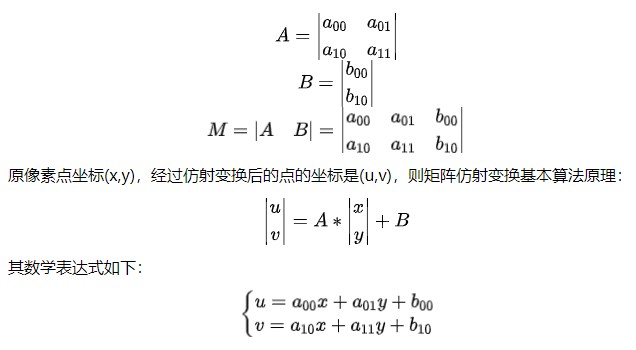
透視變換(Perspective Transformation)是將圖片投影到一個新的視平面(Viewing Plane),也稱作投影映射(Projective Mapping)。通用的變換公式為:
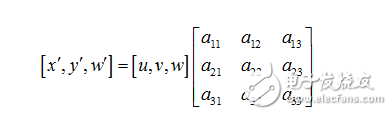
u,v是原始圖片左邊,對應得到變換后的圖片坐標x,y,其中x=x/w,y=y/w。變換矩陣

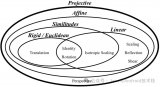
可以拆成4部分,(a11,a12,a13,a14)表示線性變換,比如scaling,shearing和ratotion。(a31,a32)用于平移,(a13,a23)T產生透視變換。所以可以理解成仿射等是透視變換的特殊形式。經過透視變換之后的圖片通常不是平行四邊形(除非映射視平面和原來平面平行的情況)。
重寫之前的變換公式可以得到:
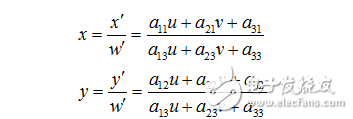
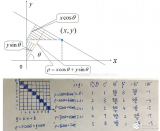
所以,已知變換對應的幾個點就可以求取變換公式。反之,特定的變換公式也能新的變換后的圖片。簡單的看一個正方形到四邊形的變換:
變換的4組對應點可以表示成:
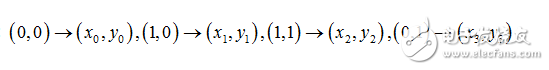
根據變換公式得到:
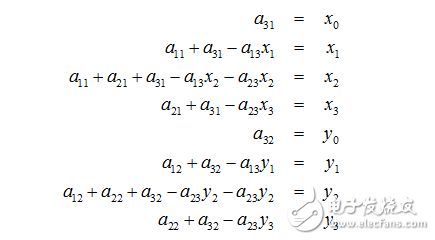
定義幾個輔助變量:
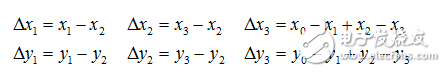
? ? ?都為0時變換平面與原來是平行的,可以得到:

不為0時,得到:
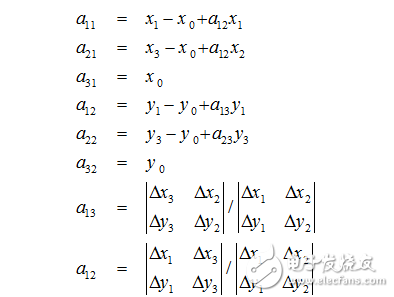
求解出的變換矩陣就可以將一個正方形變換到四邊形。反之,四邊形變換到正方形也是一樣的。于是,我們通過兩次變換:四邊形變換到正方形+正方形變換到四邊形就可以將任意一個四邊形變換到另一個四邊形。
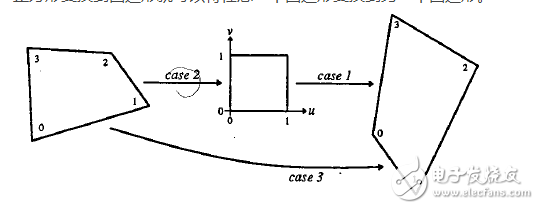
具體流程為:
a)載入圖像→灰度化→邊緣處理得到邊緣圖像(edge map)
cv::Mat im = cv::imread(filename);
cv::Mat gray;
cvtColor(im,gray,CV_BGR2GRAY);
Canny(gray,gray,100,150,3);
看一段代碼:
[cpp] view plain copy print?
PerspectiveTransform::PerspectiveTransform(float inA11, float inA21,
float inA31, float inA12,
float inA22, float inA32,
float inA13, float inA23,
float inA33) :
a11(inA11), a12(inA12), a13(inA13), a21(inA21), a22(inA22), a23(inA23),
a31(inA31), a32(inA32), a33(inA33) {}
PerspectiveTransform PerspectiveTransform::quadrilateralToQuadrilateral(float x0, float y0, float x1, float y1,
float x2, float y2, float x3, float y3, float x0p, float y0p, float x1p, float y1p, float x2p, float y2p,
float x3p, float y3p) {
PerspectiveTransform qToS = PerspectiveTransform::quadrilateralToSquare(x0, y0, x1, y1, x2, y2, x3, y3);
PerspectiveTransform sToQ =
PerspectiveTransform::squareToQuadrilateral(x0p, y0p, x1p, y1p, x2p, y2p, x3p, y3p);
return sToQ.times(qToS);
}
PerspectiveTransform PerspectiveTransform::squareToQuadrilateral(float x0, float y0, float x1, float y1, float x2,
float y2, float x3, float y3) {
float dx3 = x0 - x1 + x2 - x3;
float dy3 = y0 - y1 + y2 - y3;
if (dx3 == 0.0f && dy3 == 0.0f) {
PerspectiveTransform result(PerspectiveTransform(x1 - x0, x2 - x1, x0, y1 - y0, y2 - y1, y0, 0.0f,
0.0f, 1.0f));
return result;
} else {
float dx1 = x1 - x2;
float dx2 = x3 - x2;
float dy1 = y1 - y2;
float dy2 = y3 - y2;
float denominator = dx1 * dy2 - dx2 * dy1;
float a13 = (dx3 * dy2 - dx2 * dy3) / denominator;
float a23 = (dx1 * dy3 - dx3 * dy1) / denominator;
PerspectiveTransform result(PerspectiveTransform(x1 - x0 + a13 * x1, x3 - x0 + a23 * x3, x0, y1 - y0
+ a13 * y1, y3 - y0 + a23 * y3, y0, a13, a23, 1.0f));
return result;
}
}
PerspectiveTransform PerspectiveTransform::quadrilateralToSquare(float x0, float y0, float x1, float y1, float x2,
float y2, float x3, float y3) {
// Here, the adjoint serves as the inverse:
return squareToQuadrilateral(x0, y0, x1, y1, x2, y2, x3, y3).buildAdjoint();
}
PerspectiveTransform PerspectiveTransform::buildAdjoint() {
// Adjoint is the transpose of the cofactor matrix:
PerspectiveTransform result(PerspectiveTransform(a22 * a33 - a23 * a32, a23 * a31 - a21 * a33, a21 * a32
- a22 * a31, a13 * a32 - a12 * a33, a11 * a33 - a13 * a31, a12 * a31 - a11 * a32, a12 * a23 - a13 * a22,
a13 * a21 - a11 * a23, a11 * a22 - a12 * a21));
return result;
}
PerspectiveTransform PerspectiveTransform::times(PerspectiveTransform other) {
PerspectiveTransform result(PerspectiveTransform(a11 * other.a11 + a21 * other.a12 + a31 * other.a13,
a11 * other.a21 + a21 * other.a22 + a31 * other.a23, a11 * other.a31 + a21 * other.a32 + a31
* other.a33, a12 * other.a11 + a22 * other.a12 + a32 * other.a13, a12 * other.a21 + a22
* other.a22 + a32 * other.a23, a12 * other.a31 + a22 * other.a32 + a32 * other.a33, a13
* other.a11 + a23 * other.a12 + a33 * other.a13, a13 * other.a21 + a23 * other.a22 + a33
* other.a23, a13 * other.a31 + a23 * other.a32 + a33 * other.a33));
return result;
}
void PerspectiveTransform::transformPoints(vector《float》 &points) {
int max = points.size();
for (int i = 0; i 《 max; i += 2) {
float x = points[i];
float y = points[i + 1];
float denominator = a13 * x + a23 * y + a33;
points[i] = (a11 * x + a21 * y + a31) / denominator;
points[i + 1] = (a12 * x + a22 * y + a32) / denominator;
}
}
對一張透視圖片變換回正面圖的效果:
[cpp] view plain copy print?
int main(){
Mat img=imread(“boy.png”);
int img_height = img.rows;
int img_width = img.cols;
Mat img_trans = Mat::zeros(img_height,img_width,CV_8UC3);
PerspectiveTransform tansform = PerspectiveTransform::quadrilateralToQuadrilateral(
0,0,
img_width-1,0,
0,img_height-1,
img_width-1,img_height-1,
150,250, // top left
771,0, // top right
0,1023,// bottom left
650,1023
);
vector《float》 ponits;
for(int i=0;i《img_height;i++){
for(int j=0;j《img_width;j++){
ponits.push_back(j);
ponits.push_back(i);
}
}
tansform.transformPoints(ponits);
for(int i=0;i《img_height;i++){
uchar* t= img_trans.ptr《uchar》(i);
for (int j=0;j《img_width;j++){
int tmp = i*img_width+j;
int x = ponits[tmp*2];
int y = ponits[tmp*2+1];
if(x《0||x》(img_width-1)||y《0||y》(img_height-1))
continue;
uchar* p = img.ptr《uchar》(y);
t[j*3] = p[x*3];
t[j*3+1] = p[x*3+1];
t[j*3+2] = p[x*3+2];
}
}
imwrite(“trans.png”,img_trans);
return 0;
}

另外在OpenCV中也實現了基礎的透視變換操作,有關函數使用請見下一篇:【OpenCV】透視變換 Perspective Transformation
注意這種將原圖變換到對應圖像上的方式會有一些沒有被填充的點,也就是右圖中黑色的小點。解決這種問題一是用差值的方式,再一種比較簡單就是不用原圖的點變換后對應找新圖的坐標,而是直接在新圖上找反向變換原圖的點。說起來有點繞口,具體見前一篇《透視變換 Perspective Transformation》的代碼應該就能懂啦。
除了getPerspectiveTransform()函數,OpenCV還提供了findHomography()的函數,不是用點來找,而是直接用透視平面來找變換公式。這個函數在特征匹配的經典例子中有用到,也非常直觀:
[cpp] view plain copy print?
int main( int argc, char** argv )
{
Mat img_object = imread( argv[1], IMREAD_GRAYSCALE );
Mat img_scene = imread( argv[2], IMREAD_GRAYSCALE );
if( !img_object.data || !img_scene.data )
{ std::cout《《 “ --(!) Error reading images ” 《《 std::endl; return -1; }
//-- Step 1: Detect the keypoints using SURF Detector
int minHessian = 400;
SurfFeatureDetector detector( minHessian );
std::vector《KeyPoint》 keypoints_object, keypoints_scene;
detector.detect( img_object, keypoints_object );
detector.detect( img_scene, keypoints_scene );
//-- Step 2: Calculate descriptors (feature vectors)
SurfDescriptorExtractor extractor;
Mat descriptors_object, descriptors_scene;
extractor.compute( img_object, keypoints_object, descriptors_object );
extractor.compute( img_scene, keypoints_scene, descriptors_scene );
//-- Step 3: Matching descriptor vectors using FLANN matcher
FlannBasedMatcher matcher;
std::vector《 DMatch 》 matches;
matcher.match( descriptors_object, descriptors_scene, matches );
double max_dist = 0; double min_dist = 100;
//-- Quick calculation of max and min distances between keypoints
for( int i = 0; i 《 descriptors_object.rows; i++ )
{ double dist = matches[i].distance;
if( dist 《 min_dist ) min_dist = dist;
if( dist 》 max_dist ) max_dist = dist;
}
printf(“-- Max dist : %f ”, max_dist );
printf(“-- Min dist : %f ”, min_dist );
//-- Draw only “good” matches (i.e. whose distance is less than 3*min_dist )
std::vector《 DMatch 》 good_matches;
for( int i = 0; i 《 descriptors_object.rows; i++ )
{ if( matches[i].distance 《 3*min_dist )
{ good_matches.push_back( matches[i]); }
}
Mat img_matches;
drawMatches( img_object, keypoints_object, img_scene, keypoints_scene,
good_matches, img_matches, Scalar::all(-1), Scalar::all(-1),
vector《char》(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS );
//-- Localize the object from img_1 in img_2
std::vector《Point2f》 obj;
std::vector《Point2f》 scene;
for( size_t i = 0; i 《 good_matches.size(); i++ )
{
//-- Get the keypoints from the good matches
obj.push_back( keypoints_object[ good_matches[i].queryIdx ].pt );
scene.push_back( keypoints_scene[ good_matches[i].trainIdx ].pt );
}
Mat H = findHomography( obj, scene, RANSAC );
//-- Get the corners from the image_1 ( the object to be “detected” )
std::vector《Point2f》 obj_corners(4);
obj_corners[0] = Point(0,0); obj_corners[1] = Point( img_object.cols, 0 );
obj_corners[2] = Point( img_object.cols, img_object.rows ); obj_corners[3] = Point( 0, img_object.rows );
std::vector《Point2f》 scene_corners(4);
perspectiveTransform( obj_corners, scene_corners, H);
//-- Draw lines between the corners (the mapped object in the scene - image_2 )
Point2f offset( (float)img_object.cols, 0);
line( img_matches, scene_corners[0] + offset, scene_corners[1] + offset, Scalar(0, 255, 0), 4 );
line( img_matches, scene_corners[1] + offset, scene_corners[2] + offset, Scalar( 0, 255, 0), 4 );
line( img_matches, scene_corners[2] + offset, scene_corners[3] + offset, Scalar( 0, 255, 0), 4 );
line( img_matches, scene_corners[3] + offset, scene_corners[0] + offset, Scalar( 0, 255, 0), 4 );
//-- Show detected matches
imshow( “Good Matches & Object detection”, img_matches );
waitKey(0);
return 0;
}
代碼運行效果:

findHomography()函數直接通過兩個平面上相匹配的特征點求出變換公式,之后代碼又對原圖的四個邊緣點進行變換,在右圖上畫出對應的矩形。這個圖也很好地解釋了所謂透視變換的“Viewing Plane”。
 電子發燒友App
電子發燒友App



















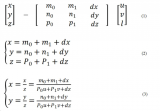










評論