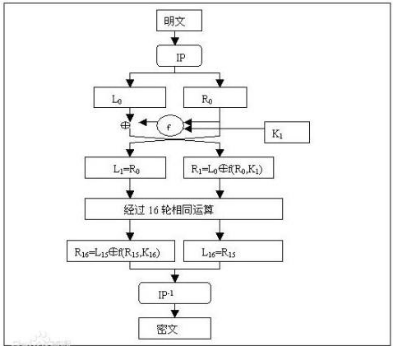
一、RSA算法?
首先, 找出三個數, p, q, r,
其中 p, q 是兩個相異的質數, r 是與 (p-1)(q-1) 互質的數
p, q, r 這三個數便是 private key
接著, 找出 m, 使得 rm == 1 mod (p-1)(q-1)
這個 m 一定存在, 因為 r 與 (p-1)(q-1) 互質, 用輾轉相除法就可以得到了
再來, 計算 n = pq
m, n 這兩個數便是 public key
編碼過程是, 若資料為 a, 將其看成是一個大整數, 假設 a 《 n
如果 a 》= n 的話, 就將 a 表成 s 進位 (s 《= n, 通常取 s = 2^t),
則每一位數均小於 n, 然後分段編碼
接下來, 計算 b == a^m mod n, (0 《= b 《 n),
b 就是編碼後的資料
解碼的過程是, 計算 c == b^r mod pq (0 《= c 《 pq),
於是乎, 解碼完畢 等會會證明 c 和 a 其實是相等的 :)
如果第三者進行竊聽時, 他會得到幾個數: m, n(=pq), b
他如果要解碼的話, 必須想辦法得到 r
所以, 他必須先對 n 作質因數分解
要防止他分解, 最有效的方法是找兩個非常的大質數 p, q,
使第三者作因數分解時發生困難
《定理》
若 p, q 是相異質數, rm == 1 mod (p-1)(q-1),
a 是任意一個正整數, b == a^m mod pq, c == b^r mod pq,
則 c == a mod pq
證明的過程, 會用到費馬小定理, 敘述如下:
m 是任一質數, n 是任一整數, 則 n^m == n mod m
(換另一句話說, 如果 n 和 m 互質, 則 n^(m-1) == 1 mod m)
運用一些基本的群論的知識, 就可以很容易地證出費馬小定理的
《證明》
因為 rm == 1 mod (p-1)(q-1), 所以 rm = k(p-1)(q-1) + 1, 其中 k 是整數
因為在 modulo 中是 preserve 乘法的
(x == y mod z and u == v mod z =》 xu == yv mod z),
所以, c == b^r == (a^m)^r == a^(rm) == a^(k(p-1)(q-1)+1) mod pq
1. 如果 a 不是 p 的倍數, 也不是 q 的倍數時,
則 a^(p-1) == 1 mod p (費馬小定理) =》 a^(k(p-1)(q-1)) == 1 mod p
a^(q-1) == 1 mod q (費馬小定理) =》 a^(k(p-1)(q-1)) == 1 mod q
所以 p, q 均能整除 a^(k(p-1)(q-1)) - 1 =》 pq | a^(k(p-1)(q-1)) - 1
即 a^(k(p-1)(q-1)) == 1 mod pq
=》 c == a^(k(p-1)(q-1)+1) == a mod pq
2. 如果 a 是 p 的倍數, 但不是 q 的倍數時,
則 a^(q-1) == 1 mod q (費馬小定理)
=》 a^(k(p-1)(q-1)) == 1 mod q
=》 c == a^(k(p-1)(q-1)+1) == a mod q
=》 q | c - a
因 p | a
=》 c == a^(k(p-1)(q-1)+1) == 0 mod p
=》 p | c - a
所以, pq | c - a =》 c == a mod pq
3. 如果 a 是 q 的倍數, 但不是 p 的倍數時, 證明同上
4. 如果 a 同時是 p 和 q 的倍數時,
則 pq | a
=》 c == a^(k(p-1)(q-1)+1) == 0 mod pq
=》 pq | c - a
=》 c == a mod pq
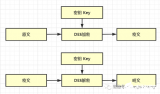
首先是密鑰對的生成:
(1)選取兩個大素數p和q(目前兩個數的長度都接近512bit是安全的)
(2)計算乘積n=p*q,Φ(n)=(p-1)(q-1),其中Φ(n)為n的歐拉函數(因為兩素數乘積的歐拉函數等于兩數分別減一后的乘積)
(3)隨機選取整數e(1《e《Φ(n))作為公鑰d,要求滿足e與Φ(n)的最大公約數為1,即兩者互素
(4)用Euclid擴展算法計算私鑰d,已滿足d * e ≡ 1 (mod Φ(n)),即d ≡ e^(-1) (mod Φ(n))。則e與n是公鑰,d是私鑰
注意:e與n應公開,兩個素數p和q不再需要,可銷毀,但絕不可泄露。
 電子發燒友App
電子發燒友App






















評論