PID的數學模型
在工業應用中PID及其衍生算法是應用最廣泛的算法之一,是當之無愧的萬能算法,如果能夠熟練掌握PID算法的設計與實現過程,對于一般的研發人員來講,應該是足夠應對一般研發問題了,而難能可貴的是,在很多控制算法當中,PID控制算法又是最簡單,最能體現反饋思想的控制算法,可謂經典中的經典。經典的未必是復雜的,經典的東西常常是簡單的,而且是最簡單的。PID算法的一般形式:
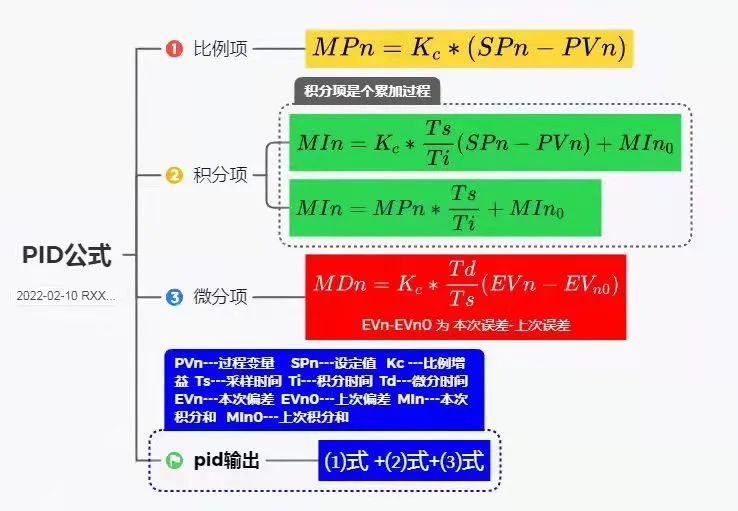
PID算法通過誤差信號控制被控量,而控制器本身就是比例、積分、微分三個環節的加和。這里我們規定(在t時刻):
?
1.輸入量為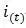
2.輸出量為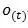
3.偏差量為?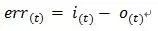
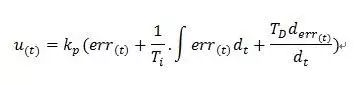
?
PID算法的數字離散化
假設采樣間隔為T,則在第K個T時刻:
偏差=?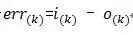
積分環節用加和的形式表示,即?
微分環節用斜率的形式表示,即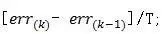
PID算法離散化后的式子:?
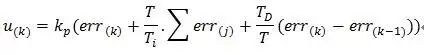
則可表示成為:
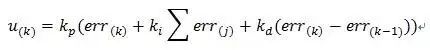
其中式中:
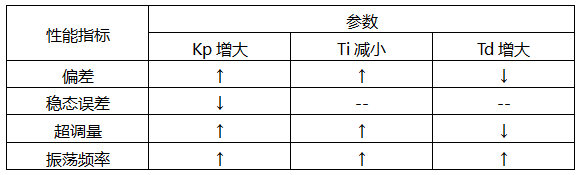
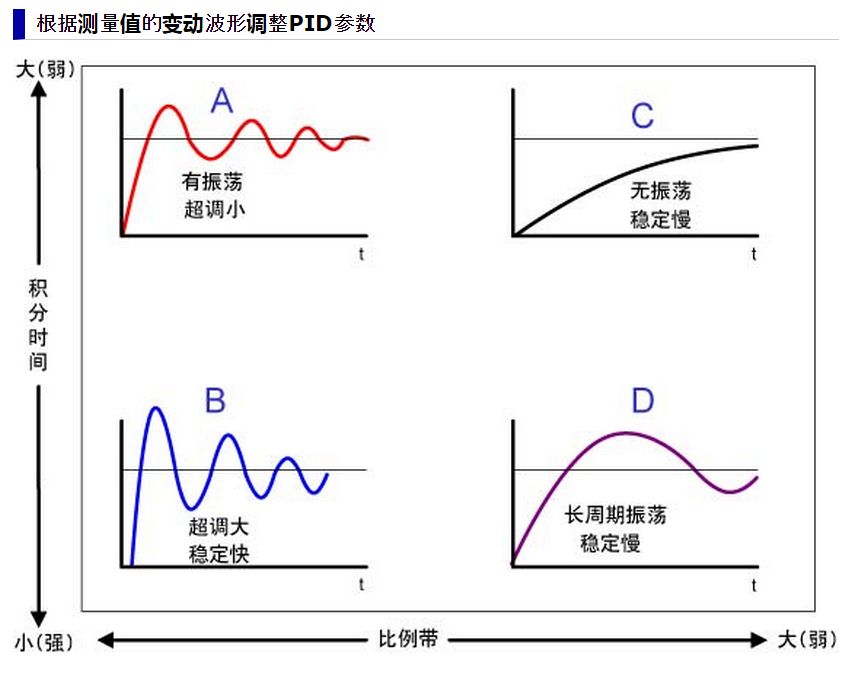
比例參數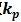 :控制器的輸出與輸入偏差值成比例關系。系統一旦出現偏差,比例調節立即產生調節作用以減少偏差。特點:過程簡單快速、比例作用大,可以加快調節,減小誤差;但是使系統穩定性下降,造成不穩定,有余差。
:控制器的輸出與輸入偏差值成比例關系。系統一旦出現偏差,比例調節立即產生調節作用以減少偏差。特點:過程簡單快速、比例作用大,可以加快調節,減小誤差;但是使系統穩定性下降,造成不穩定,有余差。
積分參數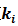 :積分環節主要是用來消除靜差,所謂靜差,就是系統穩定后輸出值和設定值之間的差值,積分環節實際上就是偏差累計的過程,把累計的誤差加到原有系統上以抵消系統造成的靜差。
:積分環節主要是用來消除靜差,所謂靜差,就是系統穩定后輸出值和設定值之間的差值,積分環節實際上就是偏差累計的過程,把累計的誤差加到原有系統上以抵消系統造成的靜差。
微分參數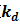 :微分信號則反應了偏差信號的變化規律,或者說是變化趨勢,根據偏差信號的變化趨勢來進行超前調節,從而增加了系統的快速性。
:微分信號則反應了偏差信號的變化規律,或者說是變化趨勢,根據偏差信號的變化趨勢來進行超前調節,從而增加了系統的快速性。
PID的基本離散表示形式如上。目前的這種表述形式屬于位置型PID,另外一種表述方式為增量式PID,由上述表達式可以輕易得到:
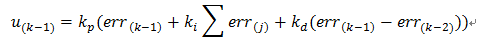
那么:
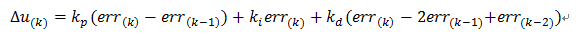
上式就是離散化PID的增量式表示方式,由公式可以看出,增量式的表達結果和最近三次的偏差有關,這樣就大大提高了系統的穩定性。需要注意的是最終的輸出結果應該為:
輸出量?=?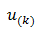 +?增量調節值
+?增量調節值
目的
PID 的重要性應該無需多說了,這個控制領域的應用最廣泛的算法了.
本篇文章的目的是希望通過一個例子展示算法過程,并解釋以下概念:
(1)簡單描述何為PID, 為何需要PID,PID 能達到什么作用。
(2)理解P(比例環節)作用:基礎比例環節。
缺點:?產生穩態誤差.
疑問: 何為穩態誤差 為什么會產生穩態誤差.
(3)理解I(積分環節)作用:消除穩態誤差.
缺點: 增加超調
疑問: 積分為何能消除穩態誤差?
(4) 理解D(微分環節)作用:加大慣性響應速度,減弱超調趨勢
疑問: 為何能減弱超調
(5)理解各個比例系數的作用
?
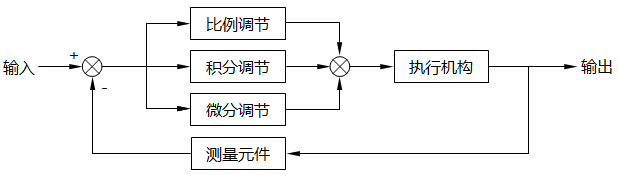
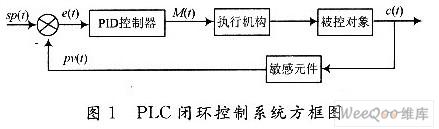
何為PID以及為何需要PID?
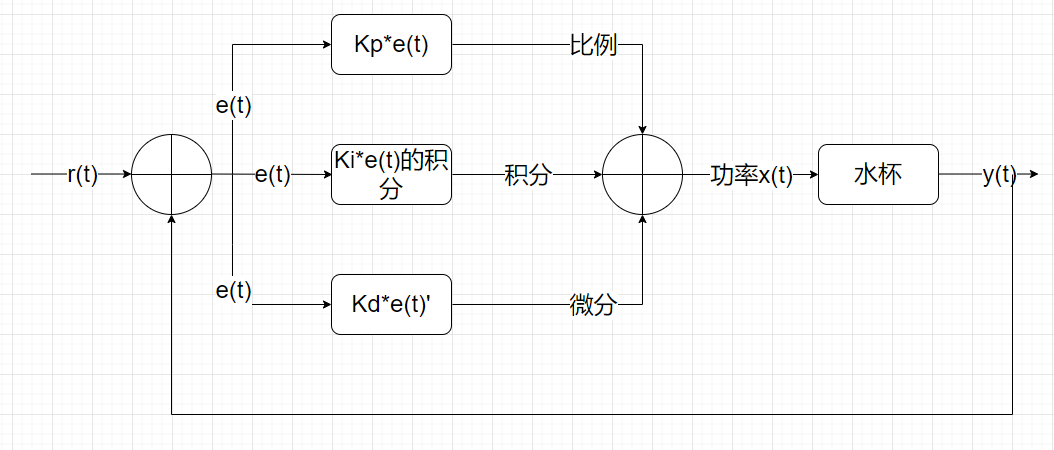
以下即PID 控制的整體框圖,過程描述為:?
設定一個輸出目標,反饋系統傳回輸出值,如與目標不一致,則存在一個誤差,PID 根據此誤差調整輸入值,直至輸出達到設定值.
疑問:
那么我們為什么需要PID 呢,比如我控制溫度,我不能監控溫度值,溫度值一到就停止嗎?
這里必須要先說下我們的目標,因為我們所有的控制無非就是想輸出能夠達到我們的設定,即如果我們設定了一個目標溫度值,那么我們想要一個什么樣的溫度變化呢.
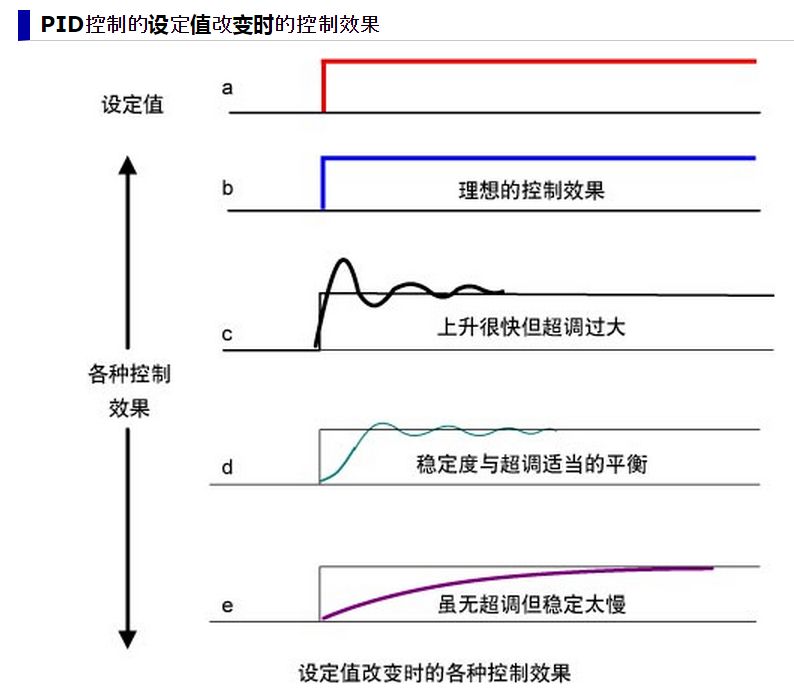
比如設定目標溫度為30度, 目標無非是希望達到圖1?希望其能夠快速而且沒有抖動的達到30度.
那這樣大家應該就明白,如果使用溫度一到就停止的辦法,當然如果要求不高可能也行,當肯定達不到圖1 這樣的要求,因為溫度到了后余溫也會讓溫度繼續升高.而且溫度自身也會通過空氣散熱的.
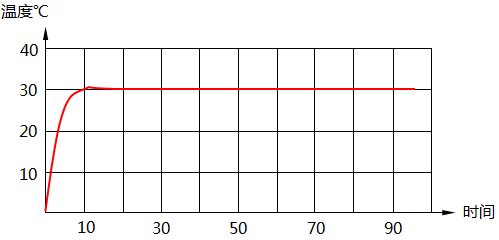
圖? 系統輸出的響應目標
綜上所述,我們需要PID的原因無非就是普通控制手段沒有辦法使輸出快速穩定的到達設定值。
控制器的P,I,D項選擇
下面將常用的各種控制規律的控制特點簡單歸納一下:
(1)、比例控制規律P:采用P控制規律能較快地克服擾動的影響,它的作用于輸出值較快,但不能很好穩定在一個理想的數值,不良的結果是雖較能有效的克服擾動的影響,但有余差出現。它適用于控制通道滯后較小、負荷變化不大、控制要求不高、被控參數允許在一定范圍內有余差的場合。如:金彪公用工程部下設的水泵房冷、熱水池水位控制;油泵房中間油罐油位控制等。
(2)、比例積分控制規律(PI):在工程中比例積分控制規律是應用最廣泛的一種控制規律。積分能在比例的基礎上消除余差,它適用于控制通道滯后較小、負荷變化不大、被控參數不允許有余差的場合。如:在主線窯頭重油換向室中F1401到F1419號槍的重油流量控制系統;油泵房供油管流量控制系統;退火窯各區溫度調節系統等。
(3)、比例微分控制規律(PD):微分具有超前作用,對于具有容量滯后的控制通道,引入微分參與控制,在微分項設置得當的情況下,對于提高系統的動態性能指標,有著顯著效果。因此,對于控制通道的時間常數或容量滯后較大的場合,為了提高系統的穩定性,減小動態偏差等可選用比例微分控制規律。如:加熱型溫度控制、成分控制。需要說明一點,對于那些純滯后較大的區域里,微分項是無能為力,而在測量信號有噪聲或周期性振動的系統,則也不宜采用微分控制。如:大窯玻璃液位的控制。
(4)、例積分微分控制規律(PID):PID控制規律是一種較理想的控制規律,它在比例的基礎上引入積分,可以消除余差,再加入微分作用,又能提高系統的穩定性。它適用于控制通道時間常數或容量滯后較大、控制要求較高的場合。如溫度控制、成分控制等。
鑒于D規律的作用,我們還必須了解時間滯后的概念,時間滯后包括容量滯后與純滯后。其中容量滯后通常又包括:測量滯后和傳送滯后。測量滯后是檢測元件在檢測時需要建立一種平衡,如熱電偶、熱電阻、壓力等響應較慢產生的一種滯后。而傳送滯后則是在傳感器、變送器、執行機構等設備產生的一種控制滯后。純滯后是相對與測量滯后的,在工業上,大多的純滯后是由于物料傳輸所致,如:大窯玻璃液位,在投料機動作到核子液位儀檢測需要很長的一段時間。
總之,控制規律的選用要根據過程特性和工藝要求來選取,決不是說PID控制規律在任何情況下都具有較好的控制性能,不分場合都采用是不明智的。如果這樣做,只會給其它工作增加復雜性,并給參數整定帶來困難。當采用PID控制器還達不到工藝要求,則需要考慮其它的控制方案。如串級控制、前饋控制、大滯后控制等。
Kp,Ti,Td三個參數的設定是PID控制算法的關鍵問題。一般說來編程時只能設定他們的大概數值,并在系統運行時通過反復調試來確定最佳值。因此調試階段程序須得能隨時修改和記憶這三個參數。
數字PID控制器
(1)模擬PID控制規律的離散化 ?

(2)數字PID控制器的差分方程
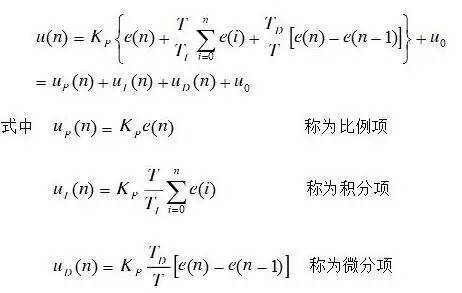
參數的自整定
在某些應用場合,比如通用儀表行業,系統的工作對象是不確定的,不同的對象就得采用不同的參數值,沒法為用戶設定參數,就引入參數自整定的概念。實質就是在首次使用時,通過N次測量為新的工作對象尋找一套參數,并記憶下來作為以后工作的依據。具體的整定方法有三種:臨界比例度法、衰減曲線法、經驗法。
1、臨界比例度法(Ziegler-Nichols)
1.1 ?在純比例作用下,逐漸增加增益至產生等副震蕩,根據臨界增益和臨界周期參數得出PID控制器參數,步驟如下:
(1)將純比例控制器接入到閉環控制系統中(設置控制器參數積分時間常數Ti =∞,實際微分時間常數Td =0)。
(2)控制器比例增益K設置為最小,加入階躍擾動(一般是改變控制器的給定值),觀察被調量的階躍響應曲線。
(3)由小到大改變比例增益K,直到閉環系統出現振蕩。
(4)系統出現持續等幅振蕩時,此時的增益為臨界增益(Ku),振蕩周期(波峰間的時間)為臨界周期(Tu)。
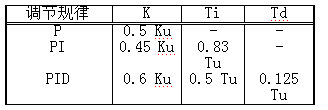
(5) 由表1得出PID控制器參數。
表1
1.2 ?采用臨界比例度法整定時應注意以下幾點:
(1)在采用這種方法獲取等幅振蕩曲線時,應使控制系統工作在線性區,不要使控制閥出現開、關的極端狀態,否則得到的持續振蕩曲線可能是“極限循環”,從線性系統概念上說系統早已處于發散振蕩了。
(2)由于被控對象特性的不同,按上表求得的控制器參數不一定都能獲得滿意的結果。對于無自平衡特性的對象,用臨界比例度法求得的控制器參數往住使系統響應的衰減率偏大(ψ>0.75 )。而對于有自平衡特性的高階等容對象,用此法整定控制器參數時系統響應衰減率大多偏小(ψ<0.75 )。為此,上述求得的控制器參數,應針對具體系統在實際運行過程中進行在線校正。
(3) 臨界比例度法適用于臨界振幅不大、振蕩周期較長的過程控制系統,但有些系統從安全性考慮不允許進行穩定邊界試驗,如鍋爐汽包水位控制系統。還有某些時間常數較大的單容對象,用純比例控制時系統始終是穩定的,對于這些系統也是無法用臨界比例度法來進行參數整定的。
(4)只適用于二階以上的高階對象,或一階加純滯后的對象,否則,在純比例控制情況下,系統不會出現等幅振蕩。
1.3 ?若求出被控對象的靜態放大倍數KP=△y/△u ,則增益乘積KpKu可視為系統的最大開環增益。通常認為Ziegler-Nichols閉環試驗整定法的適用范圍為: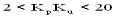
(1) 當KpKu > 20時,應采用更為復雜的控制算法,以求較好的調節效果。
(2)當KpKu < 2時,應使用一些能補償傳輸遲延的控制策略。
(3)當1.5
(4)當KpKu< 1.5時,在對控制精度要求不高的場合仍可使用PI控制器,在這種情況下,微分作用已意義不大。
2、衰減曲線法
衰減曲線法與臨界比例度法不同的是,閉環設定值擾動試驗采用衰減振蕩(通常為4:1或10:l),然后利用衰減振蕩的試驗數據,根據經驗公式求取控制器的整定參數。整定步驟如下:
(1)在純比例控制器下,置比例增益K為較小值,并將系統投入運行。
(2)系統穩定后,作設定值階躍擾動,觀察系統的響應,若系統響應衰減太快,則減小比例增益K;反之,應增大比例增益K。直到系統出現如下圖(a)所示的4:1衰減振蕩過程,記下此時的比例增益Ks及和振蕩周期Ts數值。
?
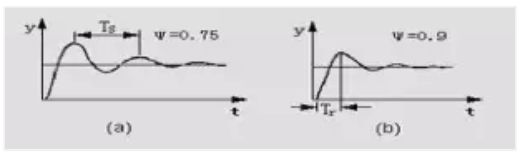
(3)利用Ks和Ts值,按下表給出的經驗公式,計算出控制器的參數整定值。?????
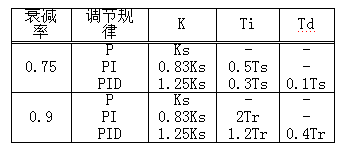
(4)10:1衰減曲線法類似,只是用Tr帶入計算。
采用衰減曲線法必須注意幾點:
(1)加給定干擾不能太大,要根據生產操作要求來定,一般在5%左右,也有例外的情況。
(2)必須在工藝參數穩定的情況下才能加給定干擾,否則得不到正確得 整定參數。
(3)對于反應快的系統,如流量、管道壓力和小容量的液位調節等,要得到嚴格的4:1衰減曲線較困難,一般以被調參數來回波動兩次達到穩定,就近似地認為達到4:1衰減過程了。
(4)投運時,先將K放在較小的數值,把Ti減少到整定值,把Td逐步放大到整定值,然后把K拉到整定值(如果在K=整定值的條件下很快地把Td放到整定值,控制器的輸出會劇烈變化)。
3、經驗整定法
3.1方法一A:
(1)確定比例增益
使PID為純比例調節,輸入設定為系統允許最大值的60%~70%,由0逐漸加大比例增益至系統出現振蕩;再反過來,從此時的比例增益逐漸減小至系統振蕩消失,記錄此時的比例增益,設定PID的比例增益P為當前值的60%~70%。
(2)確定積分時間常數
比例增益P確定后,設定一個較大的積分時間常數Ti的初值,然后逐漸減小Ti至系統出現振蕩,之后在反過來,逐漸加大Ti至系統振蕩消失。記錄此時的Ti,設定PID的積分時間常數Ti為當前值的150%~180%。
(3)確定積分時間常數Td
積分時間常數Td一般不用設定,為0即可。若要設定,與確定 P和Ti的方法相同,取不振蕩時的30%。
(4)系統帶載聯調,再對PID參數進行微調,直至滿足要求。
3.2 方法一B:
(1)PI調節
(a)純比例作用下,把比例度從較大數值逐漸往下降,至開始產生周期振蕩(測量值以給定值為中心作有規則得振蕩),在產生周期性振蕩得情況下,把此比例度逐漸加寬直至系統充分穩定。
(b)接下來把積分時間逐漸縮短至產生振蕩,此時表示積分時間過短,應把積分時間稍加延長,直至振蕩停止。
(2)PID調節
(a)純比例作用下尋求起振點。
(b)加大微分時間使振蕩停止,接著把比例度調得稍小一些,使振蕩又產生,加大微分時間,使振蕩再停止,來回這樣操作,直至雖加大微分時間,但不能使振蕩停止,求得微分時間的最佳值,此時把比例度調得稍大一些直至振蕩停止。
(c)把積分時間調成和微分時間相同的數值,如果又產生振蕩則加大積分時間直至振蕩停止。
3.3 方法二:
另一種方法是先從表列范圍內取Ti的某個數值,如果需要微分,則取Td=(1/3~1/4)Ti,然后對δ進行試湊,也能較快地達到要求。實踐證明,在一定范圍內適當地組合δ和Ti的數值,可以得到同樣衰減比的曲線,就是說,δ的減少,可以用增加Ti的辦法來補償,而基本上不影響調節過程的質量。所以,這種情況,先確定Ti、Td再確定δ的順序也是可以的。而且可能更快些。如果曲線仍然不理想,可用Ti、Td再加以適當調整。
3.4 方法三:
(1)在實際調試中,也可以先大致設定一個經驗值,然后根據調節效果修改。
流量系統:P(%)40--100,I(分)0.1--1
壓力系統:P(%)30--70,?? I(分)0.4--3
?????? 液位系統:P(%)20--80,?? I(分)1—5
溫度系統:P(%)20--60,?? I(分)3--10,D(分)0.5--3
(2)以下整定的口訣:
階躍擾動投閉環,參數整定看曲線;先投比例后積分,最后再把微分加;
理想曲線兩個波,振幅衰減4比1;比例太強要振蕩,積分太強過程長;
動差太大加微分,頻率太快微分降;偏離定值回復慢,積分作用再加強。
4、復雜調節系統的參數整定
以串級調節系統為例來說明復雜調節系統的參數整定方法。由于串級調節系統中,有主、副兩組參數,各通道及回路間存在著相互聯系和影響。改變主、副回路的任一參數,對整個系統都有影響。特別是主、副對象時間常數相差不大時,動態聯系密切,整定參數的工作尤其困難。
在整定參數前,先要明確串級調節系統的設計目的。如果主要是保證主參數的調節質量,對副參數要求不高,則整定工作就比較容易;如果主、副參數都要求高,整定工作就比較復雜。下面介紹“先副后主”兩步參數整定法。
第一步:在工況穩定情況下,將主回路閉合,把主控制器比例度放在100%,積分時間放在最大,微分時間放在零。用4:1衰減曲線整定副回路,求出副回路得比例增益K2s和振蕩周期T2s。
第二步:把副回路看成是主回路的一個環節,使用4:1衰減曲線法整定主回路,求得主控制器K1s和T1s。
根據K1s、K2s、T1s、T2s按表2經驗公式算出串級調節系統主、副回路參數。先放上副回路參數,再放上主回路參數,如果得到滿意的過渡過程,則整定工作完畢。否則可進行適當調整。
如果主、副對象時間常數相差不大,按4:1衰減曲線法整定,可能出現“共振”危險,這時,可適當減小副回路比例度或積分時間,以達到減少副回路振蕩周期的目的。同理,加大主回路比例度或積分時間,以期增大主回路振蕩周期,使主、副回路振蕩周期之比加大,避免“共振”。這樣做的結果會降低調節質量。
如果主、副對象特性太相近,則說明確定的方案欠妥當,就不能完全依靠參數整定來提高調節質量了。
實際應用體會:
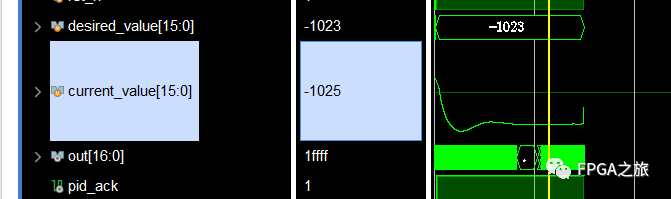
一是利用數字PID控制算法調節直流電機的速度,方案是采用光電開關來獲得電機的轉動產生的脈沖信號,單片機(MSP430G2553)通過測量脈沖信號的頻率來計算電機的轉速(具體測量頻率的算法是采用直接測量法,定時1s測量脈沖有多少個,本身的測量誤差可以有0.5轉加減),測量的轉速同給定的轉速進行比較產生誤差信號,來產生控制信號,控制信號是通過PWM調整占空比也就是調整輸出模擬電壓來控制的(相當于1位的DA,如果用10位的DA來進行模擬調整呢?效果會不會好很多?),這個實驗控制能力有一定的范圍,只能在30轉/秒和150轉/秒之間進行控制,當給定值(程序中給定的速度)高于150時,實際速度只能保持在150轉,這也就是此系統的最大控制能力,當給定值低于30轉時,直流電機轉軸實際是不轉動的,但由于誤差值過大,轉速會迅速變高,然后又會停止轉動,就這樣循環往復,不能達到控制效果。
根據實測,轉速穩態精度在正負3轉以內,控制時間為4到5秒。實驗只進行到這種程度,思考和分析也只停留在這種深度。
二是利用數字PID控制算法調節直流減速電機的位置,方案是采用與電機同軸轉動的精密電位器來測量電機轉動的位置和角度,通過測量得到的角度和位置與給定的位置進行比較產生誤差信號,然后位置誤差信號通過一定關系(此關系純屬根據想象和實驗現象來擬定和改善的)轉換成PWM信號,作為控制信號的PWM信號是先產生對直流減速電機的模擬電壓U,U來控制直流減速電機的力矩(不太清楚),力矩產生加速度,加速度產生速度,速度改變位置,輸出量是位置信號,所以之間應該對直流減速電機進行系統建模分析,仿真出直流減速電機的近似系統傳遞函數,然后根據此函數便可以對PID的參數進行整定了。
兩次體會都不是特別清楚PID參數是如何整定的,沒有特別清晰的理論指導和實驗步驟,對結果的整理和分析也不夠及時,導致實驗深度和程度都不能達到理想效果。
怎樣形象理解PID算法
小明接到這樣一個任務:
有一個水缸點漏水(而且漏水的速度還不一定固定不變)
要求水面高度維持在某個位置
一旦發現水面高度低于要求位置,就要往水缸里加水。?
小明接到任務后就一直守在水缸旁邊,時間長就覺得無聊,就跑到房里看小說了,每30分鐘來檢查一次水面高度。水漏得太快,每次小明來檢查時,水都快漏完了,離要求的高度相差很遠,小明改為每3分鐘來檢查一次,結果每次來水都沒怎么漏,不需要加水,來得太頻繁做的是無用功。
幾次試驗后,確定每10分鐘來檢查一次。這個檢查時間就稱為采樣周期。
開始小明用瓢加水,水龍頭離水缸有十幾米的距離,經常要跑好幾趟才加夠水,于是小明又改為用桶加,一加就是一桶,跑的次數少了,加水的速度也快了,
但好幾次將缸給加溢出了,不小心弄濕了幾次鞋,小明又動腦筋,我不用瓢也不用桶,老子用盆,幾次下來,
發現剛剛好,不用跑太多次,也不會讓水溢出。這個加水工具的大小就稱為比例系數。
小明又發現水雖然不會加過量溢出了,有時會高過要求位置比較多,還是有打濕鞋的危險。他又想了個辦法,在水缸上裝一個漏斗,
每次加水不直接倒進水缸,而是倒進漏斗讓它慢慢加。這樣溢出的問題解決了,但加水的速度又慢了,有時還趕不上漏水的速度。
于是他試著變換不同大小口徑的漏斗來控制加水的速度,最后終于找到了滿意的漏斗。漏斗的時間就稱為積分時間 。
小明終于喘了一口,但任務的要求突然嚴了,水位控制的及時性要求大大提高,一旦水位過低,必須立即將水加到要求位置,而且不能高出太多,否則不給工錢。
小明又為難了!于是他又開努腦筋,終于讓它想到一個辦法,常放一盆備用水在旁邊,一發現水位低了,不經過漏斗就是一盆水下去,這樣及時性是保證了,但水位有時會高多了。
他又在要求水面位置上面一點將水鑿一孔,再接一根管子到下面的備用桶里這樣多出的水會從上面的孔里漏出來。這個水漏出的快慢就稱為微分時間。
拿一個水池水位來說,我們 可以制定一個規則,
把水位分為超高、高、較高、中、較低、低、超低幾個區段;
再把水位波動的趨勢分為甚快、快、較快、慢、停幾個區段,并區分趨勢的正負;
把輸出分為超大幅 度、大幅度、較大幅度、微小幾個區段。
當水位處于中值、趨勢處于停頓的時候,不調節;
當水位處于中值、趨勢緩慢變化的時候,也可以暫不調節;
當水位處于較高、趨勢緩慢變化 的時候,輸出一個微小調節兩就夠了;
當水位處于中值、趨勢較快變化的時候,輸出進行叫 大幅度調節……。
如上所述,我們需要制定一個控制規則表,然后制定參數判斷水位區段的界值、波動趨 勢的界值、輸出幅度的界值。
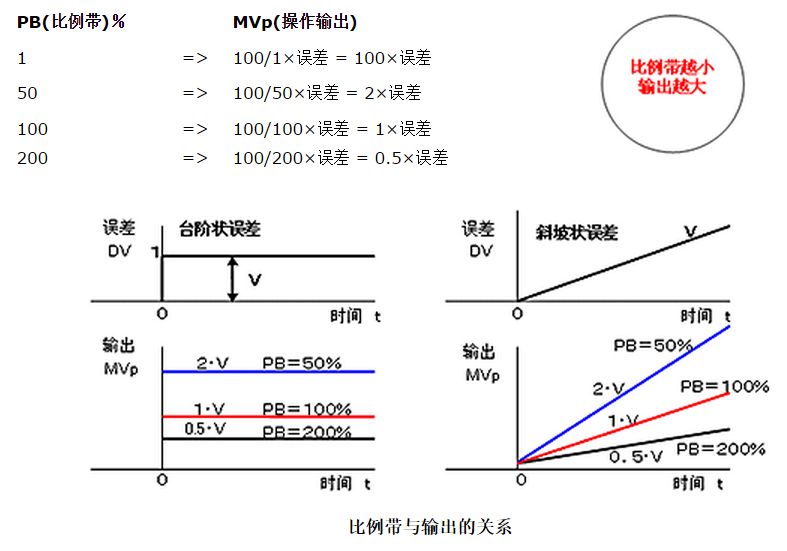
比例控制(P)是一種最簡單的控制方式。其控制器的輸出與輸入誤差信號成比例關系。
根據設備有所不同,比例帶一般為2~10%(溫度控制)。
但是,僅僅是P控制的話,會產生下面將提到的offset (穩態誤差),所以一般加上積分控制(I),以消除穩態誤差。
比例帶與比例控制(P)輸出的關系如圖所示。用MVp運算式的設定舉例:
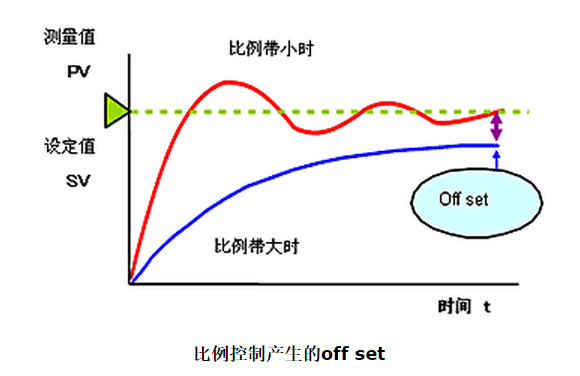
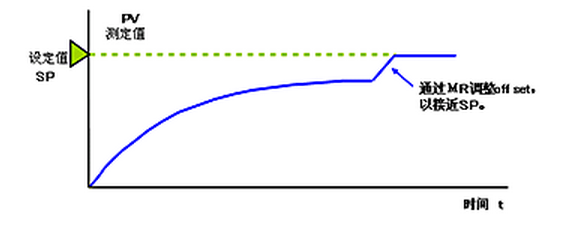
穩態誤差(Off set)
比例控制中,經過一定時間后誤差穩定在一定值時,此時的誤差叫做穩態誤差(off set)。
僅用比例控制的時候,根據負載的變動及設備的固有特性不同,會出現不同的穩態誤差。
負載特性與控制特性曲線的交點和設定值不一致是產生穩態誤差的原因。
比例帶小時不會產生。為消除穩態誤差,我們設定手動復位值--manual reset值(MR),以消除控制誤差。
手動復位(Manual reset)

如前所述,僅用比例控制不能消除穩態誤差。
為此,將MR(manual reset值)設為可變,則可自由整定(即調整)調節器的輸出。 只要手動操作輸出相當于offset的量,就能與目標值一致。
這就叫做手動復位(manual reset),通常比例調節器上配有此功能。
在實際的自動控制中,每次發生off set時以手動進行reset的話,這樣并不實用。 在后面將敘述的積分控制功能,能自動消除穩態誤差。
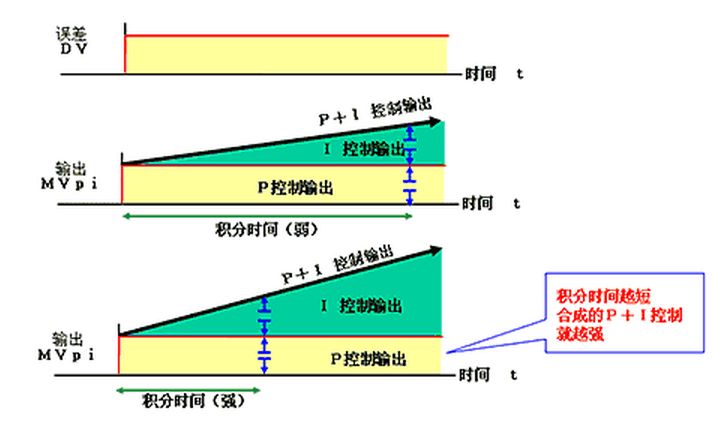
所謂積分控制(I),就是在出現穩態誤差時自動的改變輸出量,使其與手動復位動作的輸出量相同,達到消除穩態誤差的目的。
當系統存在誤差時,進行積分控制,根據積分時間的大小調節器的輸出會以一定的速度變化,只要誤差還存在,就會不斷的進行輸出。
積分時間的定義:?
當積分項和比例項對于控制器的輸出的貢獻相同,即積分作用重復了一次比例作用時所花費的時間,就是積分時間。
?
微分控制(D)的功能是通過誤差的變化率預報誤差信號的未來變化趨勢。
通過提供超前控制作用,微分控制能使被控過程趨于穩定。
? 因此,它經常用來抵消積分控制產生的不穩定趨勢。
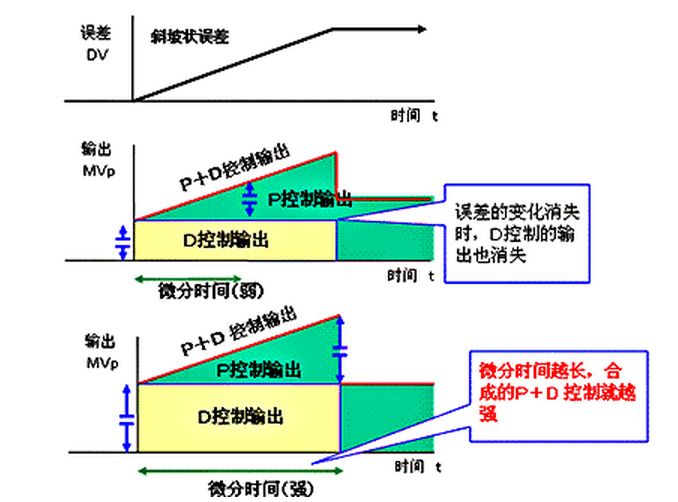
微分時間的定義:?
? 當輸入量持續的以一定速率變化時,微分項和比例項對于控制器的輸出的貢獻相同,即微分作用重復了一次比例作用時所花費的時間,就是微分時間。
實際中如何使用
我們看一個生活例子,冬天洗熱水澡,需要先放掉一段時間的冷水,因為水管里有一段冷水,熱水器也需要一個加熱過程,等過了這段時間之后水溫有些接近目標值后,開始調節水龍頭來調節冷、熱水之間的比例及出水量,之后再慢慢的微調,在洗浴過程中感覺溫度不合適,再一點點的調節。這個過程,其實就是PID算法過程。我們之所以微調,是因為水溫的變化速度與我調節的速度不相匹配,存在一個滯后效應,我們需要調節一點點,等一下再感覺一下溫度,不夠再調節一點點,再感覺,這個過程就叫PID算法,也可以說,滯后效應是引入PID的原因。
失去的能否找回來?能、只是我找回了紐扣,卻發現衣服已經不再了。這個就是滯后效應。
負反饋系統,都有滯后效應,但為什么運放、電源這類的卻從來不提PID算法呢?這是因為這類系統的滯后延時時間非常短,若考慮這個延時,負反饋引入180度相位,延時恰好引入180度相位,則完全可能引起振蕩。問題在于這個延時時間足夠短,它的諧振頻率點比較高,以運放為例,加入延時加上負反饋引起的諧振點為10MHz,但這片運放的頻率響應是1MHz,則在10MHz下完全不可能導致振蕩,因為這個芯片的頻響特性只有1MHz。我們常用的線性電源IC,比如SOT23封裝的LDO,假如輸出不加電容,就會輸出一個振蕩的波形,相對來說電源IC的滯后效應比運放要大,但是,因為電源一般后面都要接大電容的,它的頻響特性很低,接近直流0Hz,所以當有電容時候,就無法振蕩了。
而工業控制領域,比如溫度等,都是滯后效應很嚴重的,往往都是mS,甚至是10mS級別的,若直接用負反饋,因為激勵與反饋的不同步,必然導致強烈的振蕩,所以為了解決這個問題,我們需要引入PID算法,來實現這類滯后效應嚴重系統的負反饋控制,我們以高頻感應加熱設備加熱工件,從常溫25度加熱到700度為例做說明:
1、25~600度,100%的全功率加熱工件,這是因為溫差太大,前期要全功率,先加熱到靠近目標溫度。之所以考慮在600度,是因為滯后效應,若設定太高,當發現接近700度再停下來,但實際上,溫度會沖過700度。當然,600度是一個經驗值,以下幾個溫度點都是經驗值,根據實際情況而來。
2、600以上,開啟P算法,P就是根據測量值與目標值的誤差來決定負反饋的大小。P算法公式:反饋=P*(當前溫度-目標溫度)。但因為負反饋是基于存在誤差為前提的,所以P算法導致一個問題,永遠到不了想要的值:700度。因為到了700度,反饋值就沒有了。P算法的開啟,進一步逼近了目標溫度,假設穩態下可以達到650度,這樣就算因為滯后效應導致的延時,也不會超過700度太多。
3、當達到P算法的穩態極限650度附近的時候,比如640度,就應該開啟另外一個算法解決P算法引起的極限誤差,那就是I算法。I算法就是為了消除這個P算法導致的誤差值,畢竟我們想要的是700度,而不是650度。I算法,本質上講就是獲取一個700度下對應的一個驅動值,之后用這個驅動值來取代P算法,那么我們怎么得到這個驅動值呢,唯一的手段就是把之前的誤差都累加起來,最后得到一個期望值,這個期望值就是我們想要的驅動值。因為只要與目標值存在誤差,那么把這些誤差值積累起來再去反饋控制,就能一步步的逼近目標值,這如同水溫不夠高,再加一點點熱水,不夠高再加,這樣總能達到想要的水溫。值得注意的是,I算法不能接入太高,必須要在P算法的后期介入,不然很容易積累過大。這個時候可以引入一個誤差門限,比如誤差為60,當作6來處理,誤差為50,當作5來處理,消除大的誤差值,具體根據項目情況決定。
4、當I算法把工件溫度加熱到很接近目標溫度后,那么可以調節的范圍就很小了,最后一點點的微動,讓調節的每一次的變化,不要太大,這就是D算法。D算法本質上講就是反對劇烈的變化,所以適用于達到目標溫度的時候。
PID算法其實不復雜,但從目前看,很多人都是因為對這三者的使用條件不了解導致的問題,都是從加熱一開始,三個要素都上,結果可想而知。P算法是溫度接近目標值的時候用,I算法是在P算法到穩態極限的時候用,D算法是達到目標值附近的時候用。實際項目中,D算法一般不用,效果不大。假如非要找一個現實中對應的實物,那么以開關電源為例,TL431基準電源比較器可以認為是P,輸出濾波電容C是I,輸出濾波電感是D,兩者完全等價。它們各自的應用工作點可以認為:假設目標溫度700度,600~800度:P算法;640~760度:I算法;690~710度:D算法。具體值,以實驗為準,數據僅供參考。
最后給出一個PID最通俗的解讀:我們設計一樣東西,一般都是先打個樣,這個樣跟我們想要的接近,但細節沒到位,這就是P,樣有差異,所以就要修改,擬合逼近,這就是I,到了定稿,就不允許隨便修改了,就算要修改,也是有限制的修改,這就是D。 ? 編輯:黃飛
?
 電子發燒友App
電子發燒友App























評論