方案設計
采用舵機作為魔方機器人的驅動電機,從舵機的驅動原理可知:舵機運行的速度和控制器的主頻沒有關系,所以采用單片機和采用更高主頻的嵌入式處理器相比在控制效果上沒有什么差別。單片機編程過程簡單,非常容易上手,而且不需要進行操作系統的移植,非常適合對魔方機器人的舵機進行控制。 2.復原時間是魔方機器人的一個非常重要,可以說是最為重要的一個參數,本文的軟件設計中涉及到了大量的算法,如 Kocemba 復原算法和 KNN 分類算法等,而控制器主頻對于算法運行時間的長短起著決定性的作用。 所以在本文的方案設計中,我們把核心算法全部交給 Allwinner A20 運行的 APP。
設計原理
1、Kociemba算法
Kociemba算法,又稱為二階段算法,是一個使用較短時間和較少次數還原魔方的算法。按照以前網上的說法,詳細的原理可以在網頁http://kociemba.org/cube上面找到。然而現在這一個網頁也是已經不存在了,其他網站所介紹的也是非常的簡略。幸好,在我的努力之下,還是找到一些零星的資料,主要是一些外文的論文和一些github項目。通過幾天的加班閱讀,我總算是理解了大部分的內容。我把自己所理解的只是寫在這篇論文上面,希望能給和我一樣的魔方愛好者一些啟發,同時也算是一個拋磚引玉,希望能夠獲得讀者們更好的建議。
2、從魔方的狀態數說起
這篇文章討論的對象是三階魔方,原則上Kociemba算法可以變形為四階魔方的,但是這并不是本文要討論的內容。首先我們先對魔方的元素進行命名上面的約定,魔方由26個方塊組成,每個方塊由1到3個面是露在外面的,有1個面的我們稱為中心方塊,兩個面為邊,三個面的為角。通過旋轉,每個角有8中位置、3個方向,每個邊有12種位置、2個方向。我們假定魔方的中心方塊是不會移動的,也就是說,只有非中間層的面可以旋轉,以后也是不考慮中間面的旋轉。所以會產生變化的只有邊和角的位置和方向,不考慮組合的合法性,魔方的總組合為:8!12!(38)*(212)種 但是魔方會包括非法的情況,這里要考慮到魔方的狀態集的問題。我們約定魔方的所有邊和角的位置和方向為魔方的一個狀態。魔方從一個狀態通過若干次的旋轉后,魔方的新狀態一定和原狀態在一個狀態集里面。
可以證明,魔方的狀態集分成12個,每一個的總數是一樣的,所以,實際上魔方的狀態數為:8!12!(38)*(212)/12種 這個數大概是4.3萬億億,具體大小不必細究,反正非常大。如果使用最暴力的算法,例如DFS、BFS等,絕對會耗盡計算機的資源,更高階的魔方就不用說了。所以,我們要對這些狀態進行裁剪,Kociemba使用的就是因式分解的算法。打個比方,如果m=a*b,且a、b>2,那么令n=a+b,必有n
3、魔方的特殊性質
人們發現,魔方具有一些優良的性質,這些性質可以幫助將狀態數分解: 1.指定角的方向后,對于所有的面,旋轉兩次并不會改變角的方向,會有相對的兩個面(例如前和后),旋轉一次不會改變角的方向。其他面旋轉一次,會按照特定的規律變換方向,如果我們把方向編碼為0、1、2,假如某一個面的四個角原始方向按照順時針是co0、co1、co2、co3,那么如果這個面的一次旋轉會改變四個角的方向的話,對角的兩個角會變成co0+1、co2+1另外兩個對角會變成co1-1、co3-1。 2.指定邊的方向后,只有兩個相對的面的旋轉會改變邊的方向,其余面的旋轉不會改變。 下面,我們假定一次旋轉上下面不會改變魔方的角的方向,一次旋轉左右面會改變魔方邊的方向。至于具體如何編碼,我會在下下面詳細闡述。
通過這兩種性質,我們將魔方的狀態分成兩個狀態集G1、G2。其中G1狀態為魔方的原始狀態經過若干步規定以內的旋轉所組成的狀態集,這規定的旋轉包括:T、T’、D、D’、T2、D2、F2、B2、L2、R2。根據上面的假定,這些旋轉不會改變魔方8個角的方向,也不會改變12條邊的方向,而且原始狀態下中間的四條邊,在這個集合里面依然在中間層內。
根據這一個結論,我們可以將魔方的總數減少為:4!*8!*8!/12 第一個4!表示中間四條邊的位置排列,第二個8!表示上下四條邊的位置排列,第三個8!表示8個角的位置排列。在使用因式分解,總數就變為:4!+8!+8!,這個數少于10萬,并且在下面會看到,使用這一種裁剪方法會獲得較高的精度。 G2表示以G1的所有狀態為原始狀態,經過若干次任意旋轉后的狀態集,在這個狀態集里面內有什么優良的的性質可以利用,所以實際上使用了單純的裁剪手段。也是分成三組,第一組為編號為0到3的所有邊的方向和位置,第二組為編號為4到11的所有邊位置上面邊的方向,第三組為所有角的方向,所以總數為A(12,4)*(26)+28+3^8種。
4、搜索算法
Kociemba算法使用了搜索算法還原魔方。具體來說,就是先使用搜索算法轉換為G1狀態,在使用另一種搜索方式轉換為原始狀態。使用何種搜索算法對于還原魔方至關重要,搜索算法選得不好,例如使用BFS解決問題,會耗盡計算機的資源。經過前輩的不斷探索,最終改良出IDA*。所謂IDA*,就是A*算法加上迭代加深的升級版。迭代加深就是可以保證搜索樹上面的任一個節點都可以獲得精確的啟發函數值,要實現迭代加深就必須先對搜索樹上的各個節點進行預先的計算,也就是初始化。
具體到這里,就是在A*的啟發函數初始化的時候,制作一個映射表,然后通過魔方從原始狀態為起點進行若干次操作,組成一個根節點為魔方的原始狀態的、具有一定深度的操作樹。遍歷操作樹上面的所有節點,也就是每一個狀態,從表上可以映射為一個啟發函數值,其值的的大小就為節點的深度。因為此時的魔方的狀態就是魔方在原始狀態通過等于其深度的次數的操作結果,經過相反的操作當然可以還原魔方。
同時,可以知道,操作數上面必然會有狀態相同的不同節點,因為啟發函數的值應該為最小值才可以保證精度,因此,我們在遍歷操作樹的時候,使用廣度優先搜索,保證淺層的節點先被記錄,而深層的同狀態節點因為映射已經存在就會被忽略。 有了映射表,在調用啟發函數的時候,根據當前的魔方狀態,經過查表可以獲得啟發函數的值,使用A*算法判斷魔方的下一個判斷即可,同時因為迭代加深的緣故,節點的判斷函數都是準確的,不需要記錄對未搜索的可達節點。 那么,問題推到了映射表上面,如何設計高效的映射表?
5、映射表的設計
映射表只是一個概念,它代表從魔方的特定狀態向最小還原步數的映射。具體需要選擇什么實現,還需要看實際情況。實際需求可以總結為一下幾點: 1.映射表初始化后不會發生改動,也就是說不需要動態的改動映射的內容和規模。 2.映射需要一個比較高的效率。 3.映射的規模是已知的。 4.映射表應該覆蓋所有的狀態編碼組合。 第2條決定了不應該使用像std::map之類的樹型映射表,最佳方案應該是數組。因為數組查詢速度快,規模是固定的。只要我們找到一個哈希函數,將當前魔方的狀態轉換為一個整數,就可以完成映射表了。
6、方塊編碼
我認為,這一部分是算法的核心之一,之前的各種設計各種規律都是建立在這種編碼方案之上的。這說明一個好的建模方案可以大大地減少問題的難度。 首先,我要介紹角的編碼,容易知道,魔方有八個角,分別編碼為0至7,編碼與位置的對應關系與問題的解決沒有關系。同理,魔方的12條邊編碼為0值11。 真正的問題在于邊和方塊的方向問題。我們知道,邊和角的方向沒有固定的參照物,因此,我們在編碼的時候,通過規定某一些方向的方法規定方塊的方向。對于邊的方向,這比較簡單,只要是0或者1即可。
對于角,情況就有點復雜,我在這里舉個例子,說明一下編碼的過程: 我們將T、F、R面交界處的角方塊,暫稱為方塊1,方塊1的原始位置為位置1。我們要求在位置1上面的各種角方塊面,都要按照T、F、R方向的順序表示,如果1號方塊在1號位置的順序剛好就是T、F、R,那么我們認為此時1號方塊的方向就是0,除此之外,還有的可能的順序就是F、R、T和R、T、F,我們分別標號為1和2。 由于T和D旋轉是不會改變方塊的方向,所以我們可以來一個T’旋轉,是的T、F、L面交界處的角方塊,我們暫稱為方塊2,到達位置1。此時從T、F、R面上面讀取方塊2,可以讀到T、L、F。
也就是所,方塊2在順序為T、L、F的時候是0號方向,我們模仿1號方塊,認為順序L、F、T為1號方向,F、T、L為2號。同理可以知道T面的其他角。 由于F2旋轉是不活改變角的方向,所以我們進行F2旋轉,此時方塊2旋轉至F、D、R的交接面處,暫稱為位置3。此時T、L、F面的方向為D、R、F,所以我們認為方塊3的0號方向順序為D、R、F。同理可以知道D面的其他角。 通過這種建模方式,可以模仿上面說道的魔方的這些優良性質,保證搜索算法和映射表的成立。
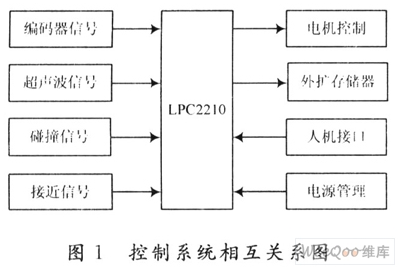
硬件設計框圖
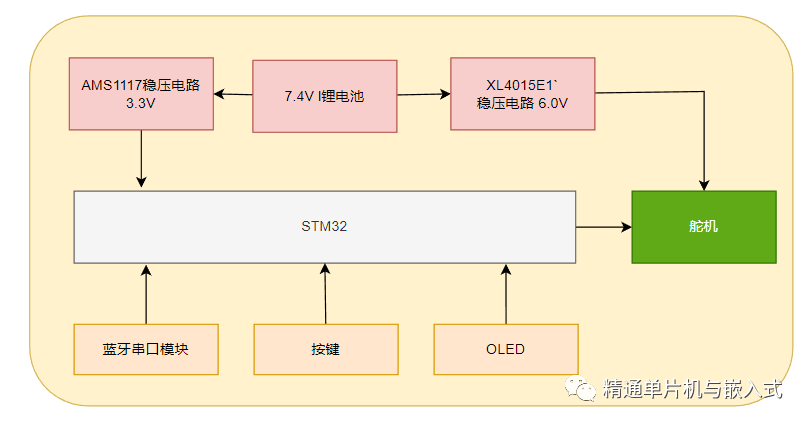
軟件設計框架
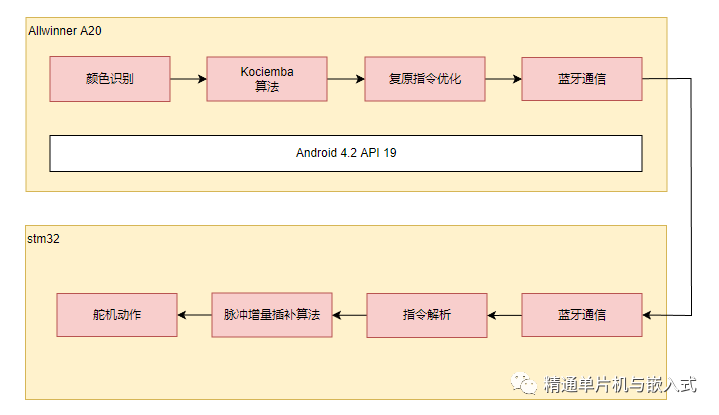
原理圖
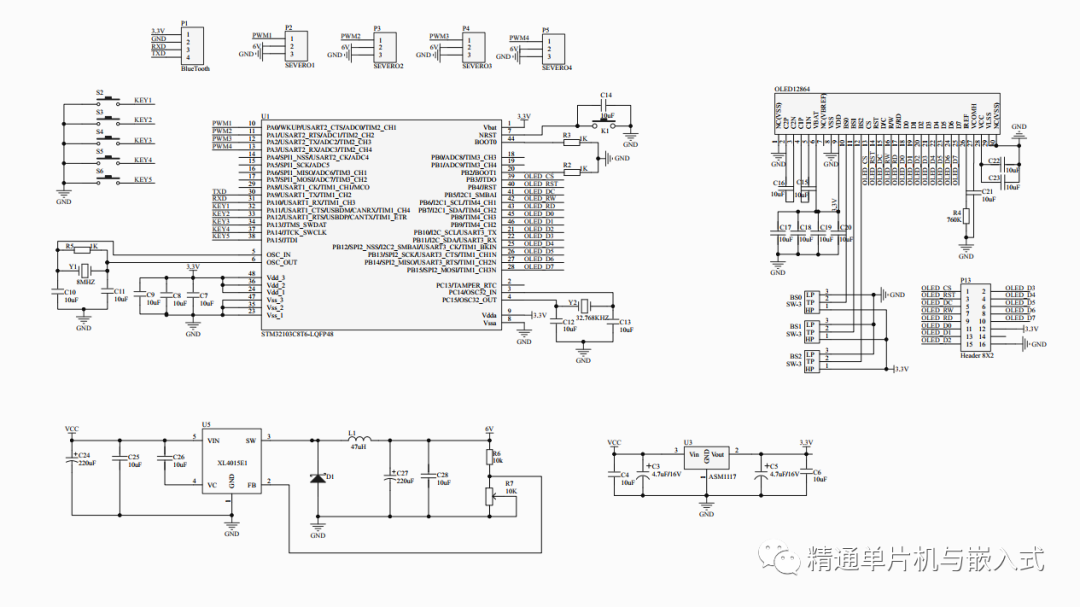
工程設計圖紙
源代碼
import kociemba as kc
import os
import cv2
import numpy as np
from copy import deepcopy
import math
def imgcheck(frame_raw):
hsv_table = [[[0, 10], [43, 255], [46, 255], '紅'],
[[156, 180], [43, 255], [46, 255], '紅'],
[[11, 20], [43, 255], [46, 255], '橙'],
[[20, 34], [43, 255], [46, 255], '黃'],
[[35, 80], [43, 255], [46, 255], '綠'],
[[80, 99], [43, 255], [46, 255], '青'],
[[100, 124], [43, 255], [46, 255], '藍'],
[[125, 155], [43, 255], [46, 255], '紫'],
[[0, 180], [0, 30], [166, 255], '白'],
[[0, 180], [0, 43], [46, 166], '灰'],
[[0, 180], [0, 255], [0, 46], '黑']]
cube_list = []
frame = frame_raw.copy()
index = 0
center = []
candidates = []
hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
for process_ind in range(2):
hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
#cv2.imshow("image", hsv)
#cv2.waitKey(0)
gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
blurred = cv2.GaussianBlur(gray, (3, 3), 0)
canny = cv2.Canny(blurred, 20, 40)
#cv2.imshow("image", canny)
#cv2.waitKey(0)
if process_ind == 0:
kernel = np.ones((3, 3), np.uint8)
dilated = cv2.dilate(canny, kernel, iterations=12)
else:
kernel = np.ones((6, 6), np.uint8)
dilated = cv2.dilate(canny, kernel, iterations=3)
if process_ind == 1 or process_ind == 0:
cv2.imshow("image", dilated)
cv2.waitKey(0)
(contours, hierarchy) = cv2.findContours(dilated.copy(), cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
hierarchy = hierarchy[0]
pre_cX = 0
pre_cY = 0
area_arr = []
for component in zip(contours, hierarchy):
contour = component[0]
peri = cv2.arcLength(contour, True)
approx = cv2.approxPolyDP(contour, 0.1 * peri, True)
area = cv2.contourArea(contour)
corners = len(approx)
# compute the center of the contour
M = cv2.moments(contour)
if M["m00"]:
cX = int(M["m10"] / M["m00"])
cY = int(M["m01"] / M["m00"])
else:
cX = None
cY = None
if cX is not None:
if process_ind == 0:
tmp = {'area': area, 'contour': contour}
area_arr.append(tmp)
elif 60000 > area > 1000:
tmp = {'index': index, 'cx': cX, 'cy': cY, 'contour': contour}
center.append(tmp)
index += 1
if process_ind == 0:
area_arr.sort(key=lambda k: (k.get('area', 0)), reverse=True)
mx,my,mw,mh = cv2.boundingRect(area_arr[0].get('contour'))
cv2.rectangle(frame, (mx,my), (mx+mw, my+mh), (0, 255, 0), 2)
#cv2.imshow("image", frame)
#cv2.waitKey(0)
frame = frame[my-5:my+mh+5, mx-5:mx+mw+5]
#cv2.imshow("image", frame)
#cv2.waitKey(0)
frame = cv2.resize(frame, (320, 320))
#if index < 9:
# return
print(str(index))
'''
center.sort(key=lambda k: (k.get('cx', 0)))
center.sort(key=lambda k: (k.get('cy', 0)))
'''
center.sort(key=lambda k: (k.get('cy', 0)))
row1 = center[0:3]
row1.sort(key=lambda k: (k.get('cx', 0)))
row2 = center[3:6]
row2.sort(key=lambda k: (k.get('cx', 0)))
row3 = center[6:9]
row3.sort(key=lambda k: (k.get('cx', 0)))
center.clear()
center = row1 + row2 + row3
for component in center:
candidates.append(component.get('contour'))
x,y,w,h = cv2.boundingRect(component.get('contour'))
if abs(w - h) < 10:
cv2.rectangle(frame, (x, y), (x+w, y+h), (0, 255, 0), 2)
#cv2.imshow("image", frame)
#cv2.waitKey(0)
h_ = 0
s_ = 0
v_ = 0
ss = w * h
for i in range(w):
for j in range(h):
h_ = h_ + hsv[y+j][x+i][0]
s_ = s_ + hsv[y+j][x+i][1]
v_ = v_ + hsv[y+j][x+i][2]
h_ = h_ / ss
s_ = s_ / ss
v_ = v_ / ss
print(str(h_) + ',' + str(s_) + ',' + str(v_))
for k in hsv_table:
if k[0][0] < h_ < k[0][1] and k[1][0] < s_ < k[1][1] and k[2][0] < v_ < k[2][1]:
# print(k[3])
cube_list.append(k[3])
break
print(str(len(cube_list)))
#if len(cube_list) == 9:
print(cube_list)
#cv2.drawContours(frame, candidates, -1, (0, 0, 255), 3)
cv2.imshow("image", frame)
cv2.waitKey(0)
if __name__ == "__main__":
webcam = cv2.VideoCapture(0)
if not webcam.isOpened():
print("can't open the camera!!!")
while True:
ret, frame = webcam.read()
rec_w = 200
rec_h = 200
rec_y = int((frame.shape[0] - rec_h)/2)
rec_x = int((frame.shape[1] - rec_w) / 2)
cv2.rectangle(frame, (rec_x, rec_y), (rec_x + rec_w, rec_y + rec_h), (0, 255, 0), 2)
imgcheck(frame)
cv2.imshow("video", frame)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
webcam.release()
cv2.destroyAllWindows()
編輯:黃飛
?
?
 電子發燒友App
電子發燒友App























評論