在實(shí)際應(yīng)用中, 直接利用DSP產(chǎn)生任意長(zhǎng)度偽隨機(jī)序列的方法, 可以為系統(tǒng)設(shè)計(jì)和測(cè)試帶來便利。文中
基于線性同余算法, 結(jié)合Analo Gdevices公司DSP芯片TigerSHARC20XS的運(yùn)算結(jié)構(gòu), 設(shè)計(jì)出一種利用尋址遞減長(zhǎng)度序列, 從而產(chǎn)生具有遍歷性的任意長(zhǎng)度偽隨機(jī)序列的方法。通過對(duì)比, 說明此方法成功解決了傳統(tǒng)方法中, 利用DSP的反饋位移寄存器只能產(chǎn)生2n (1≤n≤32)長(zhǎng)度偽隨機(jī)序列的問題, 在生成序列的任意長(zhǎng)度方面具有一定創(chuàng)新性, 對(duì)通信傳輸和雷達(dá)變頻抗干擾具有一定的參考價(jià)值。
關(guān)鍵詞 線性同余算法; 偽隨機(jī)數(shù); 任意長(zhǎng)度序列; DSP
Genera tion Method about Pseudo Random Sequence of Optiona l Cycle Ba sed on DSP
Abstract In many p rojects, it is a great advantage for designing and debugging systems to generate the p seudo random sequence by DSP. Based on the analysis of the linear congruential generator and TigerSHARC20XS of ANALOGDEV ICES, this paper p resents a method for generating the p seudo random sequence in op tional cycle by ad2 dressing the sequence of descending length. Compared with traditionalmethods, the new method, which is innova2 tive in op tional cycle, solves the p roblem that the p seudo random sequence can only be in a fixed cycle of 2n ( 1≤n≤32) using DSP in traditional methods and is of value in the transmission of communication and anti2jamming of the frequency hopp ing radar.
Keywords LCG; p seudo random number; op tional cycle sequence; DSP
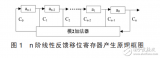
隨機(jī)數(shù)是雖然具有一定的統(tǒng)計(jì)學(xué)規(guī)律, 但抽樣值不能事先確定的數(shù)。實(shí)際中產(chǎn)生的隨機(jī)數(shù)不是絕對(duì)隨機(jī)數(shù), 而是相對(duì)的, 稱為“偽隨機(jī)數(shù)” 。偽隨機(jī)數(shù)既有隨機(jī)數(shù)所具有的優(yōu)良相關(guān)性, 又有隨機(jī)數(shù)所不具備的規(guī)律性。這兩個(gè)特點(diǎn), 使得以偽隨機(jī)數(shù)為基礎(chǔ)的偽隨機(jī)信號(hào)既易于從干擾信號(hào)中被識(shí)別和分離出來,又可以方便的產(chǎn)生和重復(fù)。因此偽隨機(jī)序列在通訊、雷達(dá)、導(dǎo)航、測(cè)量、密碼、計(jì)算機(jī)、相關(guān)辨識(shí)及故障診斷等許多領(lǐng)域中都有著廣泛的應(yīng)用。
在許多文獻(xiàn)中, 涉及的偽隨機(jī)序列產(chǎn)生方法多是基于高級(jí)語言的, 較少涉及硬件具體實(shí)現(xiàn)問題。已有的一些硬件實(shí)現(xiàn)方法, 在FPGA芯片和DSP芯片上都有過應(yīng)用 。其中在用DSP芯片實(shí)現(xiàn)時(shí), 如果要求產(chǎn)生任意長(zhǎng)度M (M > 0)的一個(gè)偽隨機(jī)序列并保證在無重復(fù)數(shù)的前提下該序列包含0~M - 1的每一個(gè)數(shù),傳統(tǒng)做法無法完成; 只有將生成的序列長(zhǎng)度M 限制為2n (1≤n ≤32)時(shí), 才能滿足要求。文中介紹的基于DSP的偽隨機(jī)序列產(chǎn)生方法解決了這樣的問題, 可以產(chǎn)生任意長(zhǎng)度的偽隨機(jī)序列, 對(duì)工程應(yīng)用有一定的現(xiàn)實(shí)意義。
1 線性同余算法的基本原理
線性同余算法[ 6 ]的核心公式是Xn + 1 = ( aXn + b) modM, n = 0, 1, ?, M - 1。其中, a ( 0≤a≤M )是 乘數(shù), b ( 0 ≤ b ≤M ) 是加數(shù), M (M > 0 ) 是模數(shù), X0 (0≤X0 ≤M )是初值即種子。模數(shù)M 也等于生成的 偽隨機(jī)序列的長(zhǎng)度, 所有參數(shù)均為整數(shù)。 線性同余算法產(chǎn)生的偽隨機(jī)序列在不更換種子的 前提下以M (M = 2n )為周期出現(xiàn)循環(huán), 如果M 不等于 2n , 序列將以
由上面的例子可以看出, 直接運(yùn)用線性同余算法用硬件產(chǎn)生偽隨機(jī)序列在實(shí)際工程應(yīng)用中并不靈活。比如在雷達(dá)信號(hào)處理中, 為了減小外界對(duì)雷達(dá)信號(hào)接收的干擾, 會(huì)要求發(fā)射機(jī)和接收機(jī)以一定的時(shí)間間隔隨機(jī)地在一定數(shù)目的頻點(diǎn)上跳頻, 在跳頻過程中不跳完所有規(guī)定的頻點(diǎn)不允許重復(fù)。如果一個(gè)頻點(diǎn)用一個(gè)偽隨機(jī)數(shù)來對(duì)應(yīng), 這就可以等價(jià)為一個(gè)偽隨機(jī)序列問題。顯然, 不能因?yàn)閭鹘y(tǒng)方法生成的偽隨機(jī)序列長(zhǎng)度必須為2n ( 1≤n ≤32) , 而要求發(fā)射機(jī)和接收機(jī)的跳頻點(diǎn)個(gè)數(shù)也設(shè)計(jì)為2n (1≤n≤32) 。
2 任意長(zhǎng)度偽隨機(jī)序列產(chǎn)生方法及DSP實(shí)現(xiàn)
由上面的舉例可以看出, 在序列長(zhǎng)度M ≠2n 的時(shí)候, 生成序列中的數(shù)都
下面結(jié)合DSP的硬件實(shí)現(xiàn)具體闡述各個(gè)步驟。首先, 用DSP程序生成一組特定長(zhǎng)度為M 的數(shù)然后放入內(nèi)存中, 這里的M 可以等于2n 也可以是任意值。也可以事先在外部文件中寫好需要輸出的一組數(shù)然后導(dǎo)入DSP的內(nèi)存中。根據(jù)不同的應(yīng)用場(chǎng)合,放入內(nèi)存的這組數(shù)可以是0~M - 1, 也可以是沒有任何規(guī)律排列的任意M 個(gè)數(shù)。
其次, 根據(jù)要求給種子、乘數(shù)、加數(shù)和模數(shù)賦值, 調(diào)用求余子程序根據(jù)線性同余算法公式進(jìn)行運(yùn)算, 得到一個(gè)余數(shù)。用得到的余數(shù)作為偏移地址, 加上已放入內(nèi)存中序列的首地址也就是基地值, 就得到了一個(gè)訪問地址。因?yàn)閯偛诺那笥嗖僮魇菍?duì)M 進(jìn)行,得到的余數(shù)即偏移地址一定
再次, 把上一步已輸出數(shù)后面的每個(gè)數(shù)都向前存放一個(gè)地址, 這樣內(nèi)存中的序列首地址不變, 序列長(zhǎng)度減1。把模數(shù)M 也減1, 以對(duì)應(yīng)新的序列長(zhǎng)度。再調(diào)用求余子程序, 根據(jù)線性同余算法公式進(jìn)行運(yùn)算,得到又一個(gè)余數(shù)。然后同樣會(huì)得到一個(gè)新訪問地址,同樣能輸出內(nèi)存中長(zhǎng)度為M - 1的序列中的某個(gè)數(shù),將其輸出。
隨后, 把上一步已輸出數(shù)后面的每個(gè)數(shù)再都向前存放一個(gè)地址, 這樣內(nèi)存中的序列首地址還不變, 序列長(zhǎng)度再減1, 把模數(shù)M 也再減1。按照剛才闡述的操作步驟重復(fù)進(jìn)行, 直至模數(shù)被減為1, 就會(huì)輸出一個(gè)符合要求的長(zhǎng)度為的偽隨機(jī)序列。此時(shí)的序列就是任意長(zhǎng)度的偽隨機(jī)序列。
最后, 如果內(nèi)存中的數(shù)都被輸出完, 重新導(dǎo)入長(zhǎng)度為M 的序列, 并更換種子 , 乘數(shù)和加數(shù)可以更換也可以不更換。然后進(jìn)入新一輪的偽隨機(jī)數(shù)生成,新生成序列中的M 個(gè)數(shù)和已生成序列中的M 個(gè)數(shù)相比較順序已經(jīng)被完全打亂。這樣一直重復(fù)操作下去,每輸出M 個(gè)數(shù)更換一次種子, 就可以生成含有M 個(gè)元素的長(zhǎng)度為n ×M ( n為正整數(shù))的偽隨機(jī)序列。
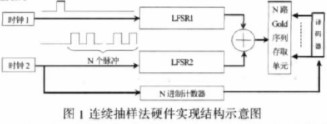
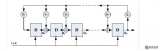
操作流程, 如圖1所示。
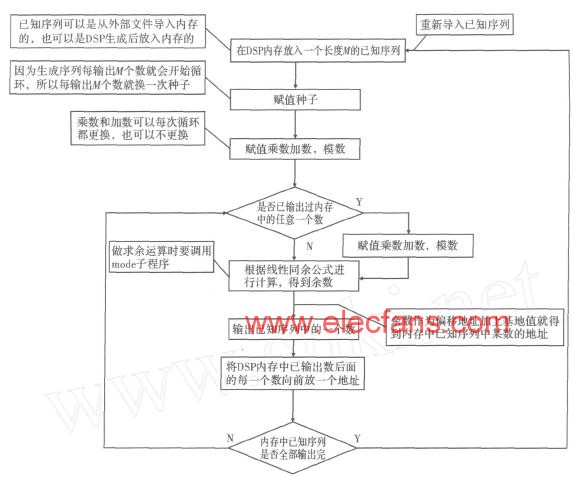
DSP主要匯編程序 。程序中以j19寄存器中所放值為基地值、長(zhǎng)度為M (M 為任意值)的一組數(shù)就是得到的長(zhǎng)度為M (M 為任意值)的偽隨機(jī)序列, 想要得到含有M 個(gè)元素的長(zhǎng)度為n ×M ( n為正整數(shù))的
偽隨機(jī)序列, 只要每隔M 個(gè)數(shù)更換種子重新運(yùn)行程序就可以得到。
當(dāng)外部文件中存有1~M 依次排列的M 個(gè)數(shù)時(shí),仿真結(jié)果舉例如下:
當(dāng)M = 8, a = b = X0 = 7時(shí), 生成序列為{ 1, 2,5, 4, 3, 8, 6, 7, 12, ...} , 周期為8; 當(dāng)M = 10,a = b = X0 = 7 時(shí), 生成序列為( 7, 3, 1, 2, 6, 5,4, 10, 8, 9, 7, 3, ...) , 周期為10; 當(dāng)M = 11,a = 5, b = 3, X0 = 4 時(shí), 生成序列為{ 2, 5, 8, 11,4, 10, 7, 9, 6, 3, 1, 2, 5, ...} , 周期為11; 當(dāng)M = 12, a = 5, b = 3, X0 = 4時(shí), 生成序列為{ 12, 2,5, 8, 11, 4, 10, 7, 9, 6, 3, 1, 12, 2, ...} , 周期為12。
由仿真結(jié)果可以看出, 文中介紹的方法能靈活產(chǎn)生任意長(zhǎng)度的偽隨機(jī)序列。
3 結(jié)束語
偽隨機(jī)序列有著廣泛的應(yīng)用前景, 在通信傳輸和雷達(dá)抗干擾方面尤為重要, 序列長(zhǎng)度是影響其應(yīng)用的關(guān)鍵因素。文中討論了偽隨機(jī)序列長(zhǎng)度和遍歷性的矛盾, 提出了基于DSP芯片具有遍歷性的任意長(zhǎng)度偽隨機(jī)序列的工程實(shí)現(xiàn)方法。給出了對(duì)該實(shí)現(xiàn)方法具體步驟的分析, DSP程序的仿真結(jié)果顯示了該實(shí)現(xiàn)方法的正確性和有效性。在應(yīng)用中可方便地修改程序中各參數(shù), 以滿足各種場(chǎng)合不同的需求。
參考文獻(xiàn)
[ 1 ] 束禮寶, 宋克柱, 王硯方. 偽隨機(jī)數(shù)發(fā)生器的FPGA實(shí)現(xiàn)與研究. 電路與系統(tǒng)學(xué)報(bào), 2003, 8 (3) : 121.
[ 2 ] 章瀲, 秦會(huì)斌. 基于FPGA偽隨機(jī)碼發(fā)生器的實(shí)現(xiàn).電子與封裝, 2008, 8 (2) : 43 - 45.
[ 3 ] 張瑞華, 劉慶華, 周德新. 偽隨機(jī)噪聲產(chǎn)生算法及DSP實(shí)現(xiàn). 聲學(xué)與電子工程, 2003 (2) : 22 - 23.
[ 4 ] 賈銀潔, 趙麗娟, 許鵬飛. 擴(kuò)頻系統(tǒng)中偽隨機(jī)碼發(fā)生器的實(shí)現(xiàn). 現(xiàn)代計(jì)算機(jī), 2008 (5) : 72 - 73.
[ 5 ] 吳浩, 郝燕玲, 徐定杰. DSP在偽隨機(jī)序列發(fā)生器中的應(yīng)用. 應(yīng)用科技, 2002, 29 (8) : 43 - 44.
[ 6 ] 馬華, 張曉清, 張鵬鴿. 一種基于線性同余算法的偽隨機(jī)數(shù)產(chǎn)生器. 純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué), 2005, 21 ( 9) :206 - 207.
[ 7 ] 茅以海. 頻率捷變雷達(dá). 北京: 國防工業(yè)出版社, 1981.
[ 8 ] 韓建輝. 雷達(dá)抗干擾中隨機(jī)數(shù)產(chǎn)生技術(shù)分析研究.雷達(dá)與對(duì)抗, 2006 (1) : 9 - 11.
[ 9 ] 林象平. 雷達(dá)對(duì)抗原理. 西安: 西北電訊工程學(xué)院出版社, 1985.
[ 10 ] 劉書明, 羅勇江. ADSP TS20XS系列DSP原理與應(yīng)用設(shè)計(jì). 北京: 電子工業(yè)出版社, 2007.
 電子發(fā)燒友App
電子發(fā)燒友App










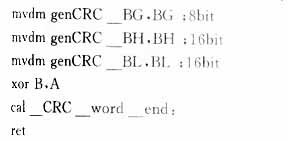
















評(píng)論