FPGA的Kalman濾波器的設計
摘要:針對電路設計中經常碰到數據的噪聲干擾現象,提出了一種Kalman濾波的FPGA實現方法。該方法采用了TI公司的高精度模數轉換器ADSl25l以及Altera公司的EPlCl2,首先用卡爾曼濾波算法設計了一個濾波器,然后將該濾波器分解成簡單的加、減、乘、除運算。通過基于FPGA平臺的硬件與軟件的合理設計,成功地實現了數據噪聲的濾除設計,并通過實踐仿真計算,驗證了所實現濾波的有效性。
??? 卡爾曼濾波是一個“Optimal Recursive Data Processing Algorithm(最優化自回歸數據處理算法)”,對于解決很大部分的問題,是最優化的,效率最高甚至是最有用的。傳統的卡爾曼濾波是在DSP上實現的。但是DSP成本相對較高,而且指令是串行執行的,不能滿足有些要求較高的場合。而FPGA由于其硬件結構決定了它的并行處理方式,無論在速度還是實時性都更勝一籌。文中以基于FPGA器件和A/D轉換器的數據采集系統為硬件平臺,進行了卡爾曼濾波算法設計,詳述了基于FPGA的卡爾曼濾波器的設計實現。
1 卡爾曼濾波算法
??? 工程中,為了了解工程對象(濾波中稱為系統)的各個物理量(濾波中稱為狀態)的確切數值,或為了達到對工程對象進行控制的目的,必須利用測量手段對系統的各個狀態進行測量。但是,量測值可能僅是系統的部分狀態或是部分狀態的線性組合,且量測值中有隨機誤差(常稱為量測噪聲)。最優估計就是針對上述問題的一種解決方法。它能將僅與部分狀態有關的測量進行處理,得出從統計意義上講誤差最小的更多狀態的估值。誤差最小的標準常稱為估計準則,根據不同的估計準則和估計計算方法,有各種不同的最優估計,卡爾曼濾波是一種遞推線性最小方差估計的最優估計。
??? 系統的狀態方程可設定為
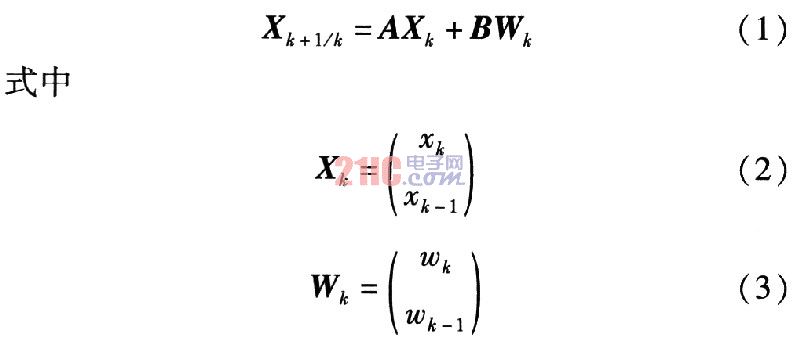
式(3)為系統噪聲。設設備的量測噪聲為Vk,系統得量測方程為

式中,![]() 是利用當前狀態預測的結果,
是利用當前狀態預測的結果,![]() 是當前狀態最優的結果,Pk+1/k是
是當前狀態最優的結果,Pk+1/k是![]() *對應的covariance,Rk是對應的covanance,表示A的轉置矩陣,Q是系統過程的covariance。式(1),式(2)就是卡爾曼濾波器5個公式中的前兩個,也就是對系統的預測。可以得到將來狀態k+l的最優化估算值。
*對應的covariance,Rk是對應的covanance,表示A的轉置矩陣,Q是系統過程的covariance。式(1),式(2)就是卡爾曼濾波器5個公式中的前兩個,也就是對系統的預測。可以得到將來狀態k+l的最優化估算值。
??? 式(9)中I為單位矩陣,對于單模型單測量,I=1。當系統進入k+2狀態時,Pk+1就是式(2)的Pk。這樣,算法就可以自回歸的運算下去。
??? R為測量數據的方差;Q為系統過程噪聲的方差,取值為![]() ,根據經驗可設置為測量數據方差的1/10;P的初值可選為單位陣,I為單位陣,X的處置可選為(0,0)T。算法示意圖,如圖1所示。
,根據經驗可設置為測量數據方差的1/10;P的初值可選為單位陣,I為單位陣,X的處置可選為(0,0)T。算法示意圖,如圖1所示。
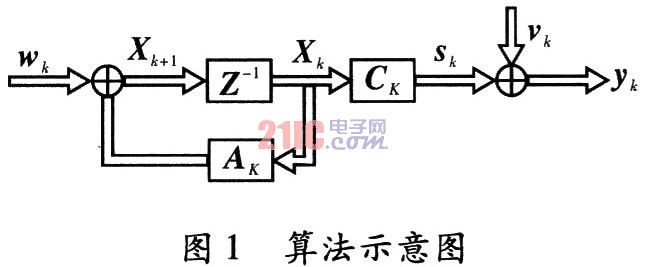
??? 將算法矩陣展開并寫成乘加形式,令
?
|
|
|
|
?
??? 這些公式包含了一些加、減、乘、除的數學運算,用FPGA實現卡爾曼濾波就是用FPGA實現這些運算。
2 硬件設計
2.1 A/D選擇
??? ADSl251是TI公司生產的一種高精度、寬動態范圍的24位△~∑乏結構的模數轉換器。采樣保持器的輸入形式采用差分模擬輸入方式,設計了一個簡單的電平轉換電路使得端和端之間的電壓波動范圍為士2.5 V。ADSl251的時鐘頻率由8 MHz的外部晶振提供,系統時鐘由FPGA給出。ADSl251的內部結構圖,如圖2所示。
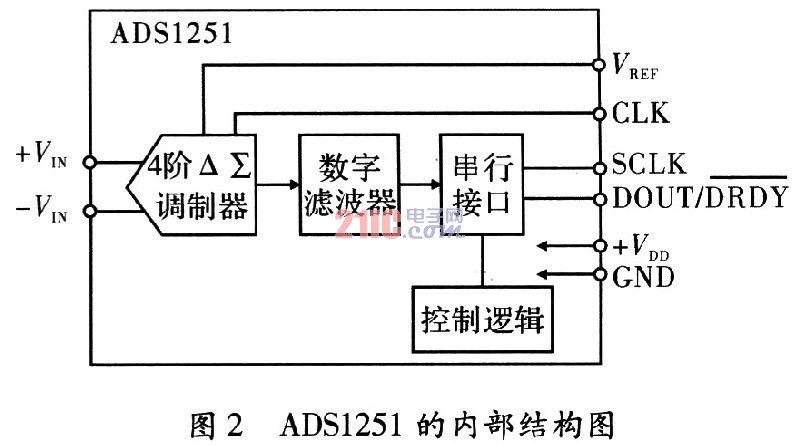
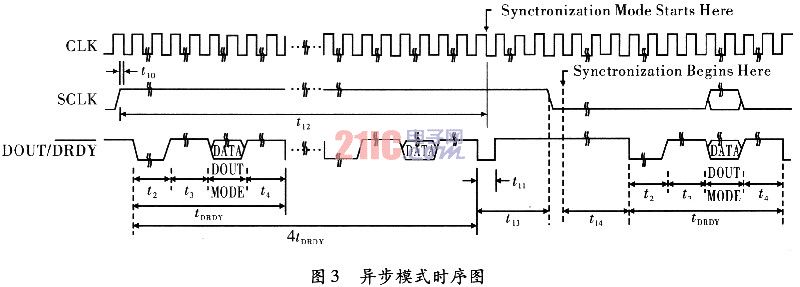
??? 輸出有3種模式:同步、異步及掉電模式,異步模式與Kalman濾波器數據輸入接口連接比較方便。其時序如圖3所示。
?
2.2 FPGA設計
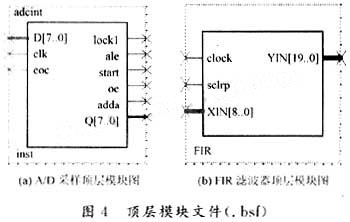
??? FPGA的特點在于靈活,通用。如果資源夠用,可以實現各種數字組合,包括CPU。本系統采用的:FPGA是Ahera公司低價位的EP1C12,該芯片內含有兩個PLLs,12060LEs及239616 Total RAMbits。在本系統的設計中,FPGA內主要實現以下幾個功能:Kalman狀態控制信號、Kalm-an濾波運算、A/D控制模塊、時鐘及波特率設置等。卡爾曼濾波器的系統結構圖,如圖4所示。

??? 通過A/D轉換芯片采集轉換數據后,進入FPGA的A/D控制模塊,在Kalman狀態控制信號的作用下,進行濾波運算,然后通過控制接口將濾波數據輸出。由此可見,卡爾曼濾波的實現包括兩部分:Kalman狀態控制信號和Kalman濾波運算。
3 Kalmaft濾波器的設計
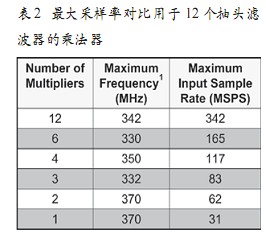
??? 在FPGA中實現Kalman濾波器,重點在于平衡資源利用率和處理速度、數據運算精度之間的矛盾,難點在于浮點加、減、乘、除的硬邏輯及卡爾曼濾波流程控制的實現。一般地,實際應用中,數字采樣重復頻率是待采樣信號最高頻率成分的5倍以上能保證較好恢復原信號,本設計中出于后期升級的考慮,將采樣率設置在800次/s,是輸出信號帶寬的20倍。
??? 通過第2節中的分解,Kalman濾波器由16次加法、20次乘法、1次除法以及必要的輸入、輸出及循環控制組成,共45步。狀態控制器(Kal-man狀態控制信號)實際是一個有限狀態機,分別控制濾波器中的45步運算,決定其執行順序,每一步利用計數器為其提供必要的時鐘周期。
??? Kalman濾波運算主要是浮點計算,浮點表示常用的標準是IEEE 754,IEEE二進制浮點數算術標準(IEEE754)是最廣泛使用的浮點數運算標準,為許多CPU與浮點運算器所采用。IEEE 754規定了4種表示浮點數值的方式:單精確度(32位元)、雙精確度(64位元)、延伸單精確度(43位元以上,較少使用)與延伸雙精確度(79位元以上,通常以80位元實做)。
??? 二進制浮點數是以符號數值表示法格式儲存,將最高效位元指定為符號位元(Sign Bit);“指數部分”,即次高效的e位元,為浮點數中經指數偏差(Exponent Bias)處理過后的指數;“小數部分”,即剩下的f位元,為有效位數(Significand)減掉有效位數本身的最高效位元,如圖5所示。

??? 文中采用的單精度二進制小數,使用32個位元存儲,如圖6所示。

其中,31位是符號位;0表示正;1表示負;30~23位為階數;22~0表示數值的有效位。偏正值為+127。其表示的具體值可用式(27)表示
??? 
??? 指數部分采用一個無符號的正數值存儲。單精度的指數部分是-126~+127加上127,指數值的大小為1~254(0和255是特殊值)。浮點小數計算時,指數值減去偏正值將是實際的指數大小。
??? 由于資源的限制,濾波中的運算過程只能以有限的精度進行,但過低的精度容易引起濾波發散,同時為了兼顧A/D高達24 bit的分辨率精度,在IEEE754單精度浮點數格式的基礎上按照浮點表示的原則做了改造,將指數部分減少到6位,尾數增加到25位,25位尾數可以完全表示A/D輸出的24位采樣值,并削弱舍入誤差的影響,其格式如圖7所示。
?

??? 本系統對處理速度的要求并不高,運算部件的設計并不考慮速度優化。
??? 加法器按以下通用的規則設計:
??? (1)階碼相減:兩個操作數階碼相減,求得階差d=|Ea-Eb|;
??? (2)尾數對齊:階碼小的操作數的尾數右移d位;
??? (3)尾數相加:完成移位處理后的尾數相加運算;
??? (4)轉換:尾數相加的結果為負數時,轉換為符號尾數的表示方式;
??? (5)前導0/1的判定:判定由于減法結果產生的左移位數,對于加法判定是否右移一位或不移,對前導0/1判定的結果進行編碼以驅動規格化移位;
??? (6)規格化:規格化有效位并且根據移位的方向和位數修改最終的階碼Ef;
??? (7)舍入:根據IEEE標準判定最終結果的舍入,如果需要入,則最末有效位加1;如舍入引起溢出,則需要有效位右移1位,同時階碼Ef加1。
??? 乘法器的設計相對簡單,與加法器一樣采用簡單的設計規則:
??? (1)指數相加:完成兩個操作數的指數相加運算;
??? (2)尾數調整:將尾數f調整為l/f的補碼格式;
??? (3)尾數相乘:完成兩個操作數的尾數相乘運算;
??? (4)規格化:根據尾數運算結果調整指數位,對尾數進行舍入截位操作,規格化輸出結果。
??? 采用Altera提供的IP核,除法器能完成IEEE754單精度除法運算。數據進入該除法器前需要將自定義的浮點格式的階碼擴展為8位加上95,尾數右移兩位,轉換為標準單精度浮點,計算結果再由標準單精度浮點的按相反的方法轉換為自定義浮點。
??? 文中硬件編程語言是用Verilog實現的。
4 實測結果分析與結論
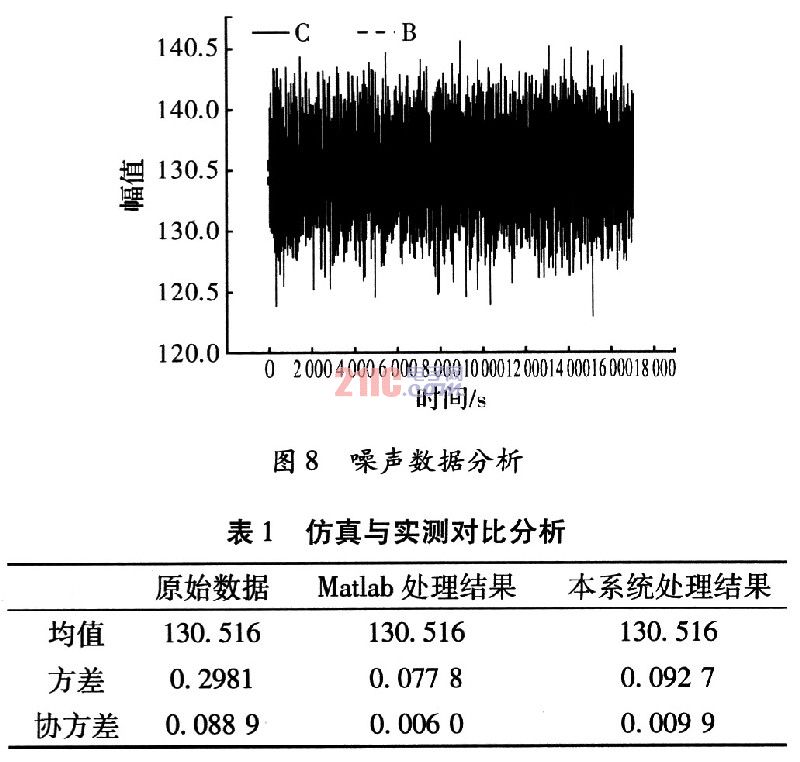
??? 從系統輸出數據中隨機抽取一段數據用Matlab分析,其結果如圖8所示。實線C表示的是濾波前的噪聲:虛線B表示的是濾波后的噪聲。很容易看出經過濾波后噪聲降低了很多。仿真與實測對比分析如表1所示。
?
5 結束語
??? 卡爾曼濾波器在很多領域具有重要的作用,可以實現數字信號處理功能,并能滿足實時性的要求。用FPGA實現Kalman濾波過程,實現簡便、成本較低、濾波效果好,被廣泛應用于圖像視頻、陀螺慣導去噪、電子羅盤、雷達接收機目標跟蹤處理、目標預測等圖像、數據采集與處理領域。
 電子發燒友App
電子發燒友App







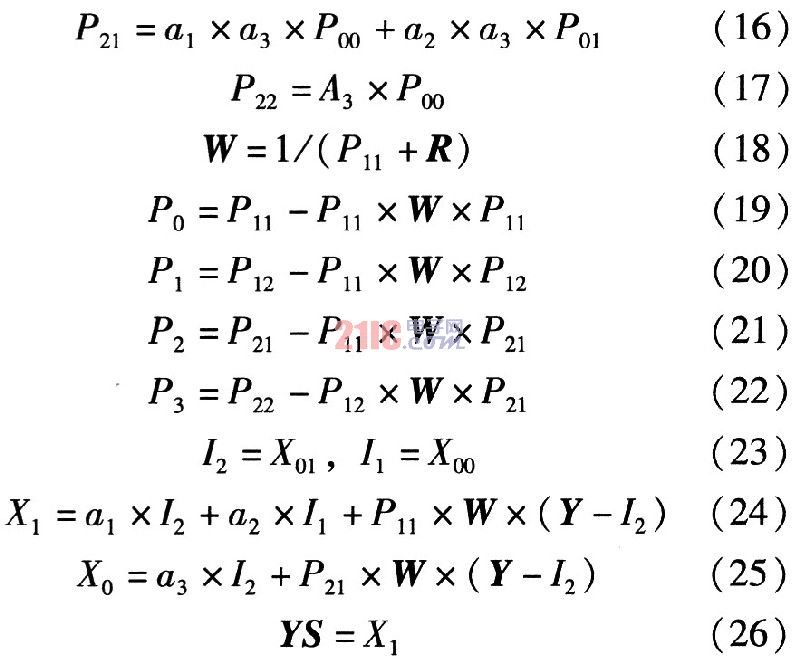





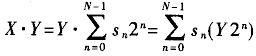













評論