雖然CORDIC 是實現 DSP 和數學函數最重要的算法之一,但許多設計人員并不熟悉。
大多數工程師在碰到需要在 FPGA 中實現諸如正弦、余弦或開平方這樣的數學函數時,首先會想到的是用查找表,可能再結合線性內插或者冪級數(如果有乘法器可用)。不過對這種工作來說,CORDIC 算法是工具庫中最重要的工具之一,只是鮮有工程師知曉。
CORDIC 的意思是坐標旋轉數字計算機, 是 JackVolder 在 1959 年為康維爾公司 (Convair) B-58A“盜賊”項目設計新的導航計算機時發明的。這是一種設計用于計算數學函數、三角函數和雙曲函數的簡單算法。
這種算法的真正優勢在于只需要采用極小型的 FPGA封裝就可以實現它。CORDIC 只需要一個小型查找表,加上用于執行移位和加法的邏輯。重要的是這種算法不需要專門的乘法器或除法器。
這種算法是 DSP 以及工業與控制應用最有用的工具之一,其最為常見的用途是實現如表 1 所示的傳統數學函數,可在器件缺少專用乘法器或 DSP 模塊的情況下提供器件所需的乘法器、除法器或更有意義的函數。舉例來說,設計人員在眾多小型工業控制器中使用 CORDIC 來實現數學傳遞函數和真正的 RMS 測量。工程師也在生物醫學應用中使用 CORDIC 來進行快速傅里葉變換 (FFT) 計算,以分析多種生理信號的頻譜。在本應用中,結合傳統的數學函數,設計人員使用 CORDIC 實現 FFT 旋轉因子。

CORDIC 詳解
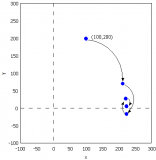
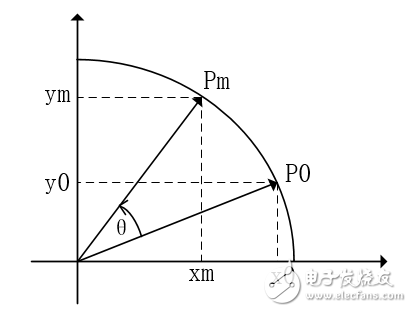
CORDIC 算法可以采用線性、圓或雙曲線三種配置中的任何一種進行運算。而對于每種配置,算法又可以在旋轉或向量任一模式下執行。在旋轉模式下,輸入向量按一定的角度旋轉,而在向量模式下,算法將輸入向量旋轉到 X 軸,同時記錄旋轉角度。
另外,可以從 CORDIC 的輸出求出其它函數。許多情況下,甚至可以使用另一個配置截然不同的 CORDIC來實現這些函數,如下所示:

下面的統一算法涵蓋了 CORDIC 的所有三種配置。該算法有 X、Y 和 Z 三種輸入。表 2 是根據配置預先計算的查找表值,表 3 則是根據運算模式(向量或旋轉)在啟動時的初始化方式。



其中m表示雙曲線(m=-1),線性(m=0)或旋轉(m=1)配置。ei 值則為不同配置下的對應的旋轉角度。ei 值一般在FPGA 中通過小查找表實現,如表 2 所示。
在這個等式中,di 為旋轉方向,這取決于運算模式。在旋轉模式下,如果 Zi < 0,則 di = -1,否則 di = +1;在向量模式,如果 Yi < 0,則 di = +1,否則 di = -1。
在圓函數旋轉模式或雙曲線旋轉模式下,輸出結果將有增量,這部分增量可以通過下面等式中定義的旋轉次數來預先求得。
這部分增量一般反饋到算法的初始設置中,以免對結果進行后縮放。
設計人員在工作時必須牢記 CORDIC 算法只能在嚴格收斂域內運算。可能需要進行一定的預縮放,以確保其能夠按預期執行。需要指出的是,決定執行的迭代(串行)或級數(并行)的次數越多,得到的運算結果就越準確。經驗法則告訴我們,如果需要 n 位的精度,就需要進行 n 次迭代或 n 個級數。不過在橫切代碼前,所有這些都可以采用諸如 Excel 或 MATLAB? 等簡易工具輕松完成建模,從而確保能夠用選定的迭代次數得到精確的結果。
根據定義,CORDIC 算法只能在有限的輸入值范圍內收斂(工作)。對采用圓函數配置的 CORDIC 算法而言,只要角度不大于查找表中的角度之和(即在 -99.7°到99.7°之間)即可保證收斂。對大于這個范圍的角度,必須使用三角恒等式將其轉換為這個范圍內的角度。采用線性配置時,其收斂亦如此。但是,要實現雙曲線配置下的收斂,必須重復進行一定數量的迭代(4、13、40、K…3K+1)。在這種情況下最大輸入值 θ 約為 1.118 弧度。
CORDIC 應用
設計人員在從數字信號處理和圖像處理到工業控制等多種應用中采用CORDIC 算法。最基本的用法是將CORDIC 與相位累加器結合,以生成正弦波和余弦波,供 I 調制和 Q 調制使用。使用該算法生成這些波形,如果生成正確,可以實現高度的無雜散動態范圍 (SFDR)。對大多數信號處理應用而言,需要良好的無雜散動態范圍。
在機器人技術領域,CORDIC 被用于運動學領域,對判斷機器人的關節、四肢的位置和運動非常有用。在該應用中,可以使用圓函數向量模式的 CORDIC 算法輕松將坐標值與新坐標值相加。在圖像處理領域,像光照和向量旋轉這樣的三維運算最好選用該算法來實現。
在 EXCEL 中建模
在橫切代碼前,建立 CORDIC 算法模型最直觀的方法之一是填制簡單的Excel 數據表。這樣可以先用浮點數系統,再用可擴展的定點數系統為迭代次數和增量(An)建模,以便為仿真過程中的代碼驗證提供參考。
從表 4 的 Excel 模型中可以看到,將初始的 X 輸入設為 An,可以減少結果后處理工作量。初始自變量設為 Z,單位為弧度,和結果一樣。

實現 CORDIC
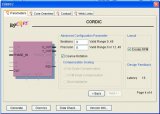
如果沒有其他更好的選擇,在 FPGA中實現 CORDIC 算法的最簡單方法就是使用像賽靈思 CORE Generator?這樣的工具。CORE Generator 提供了全面的接口,供用戶定義 CORDIC的確切功能(旋轉、向量等),如圖1 所示。

令人遺憾的是,CORE Generator 不提供 CORDIC 在線性模式下工作的選項(該工具確實提供有執行這些功能的獨立內核)。不過只需要幾行就可以編寫出實現該算法:
LIBRARY ieee;
USE ieee.std_logic_1164.all;
USE ieee.numeric_std.all;
ENTITY synth_cordic IS PORT(
clk : IN std_logic;
resetn : IN std_logic;
z_ip : IN std_logic_vector(16 DOWNTO
0); --1,16
x_ip : IN std_logic_vector(16 DOWNTO 0);
--1,16
y_ip : IN std_logic_vector(16 DOWNTO 0);
--1,16
cos_op : OUT std_logic_vector(16 DOWNTO
0); --1,16
sin_op : OUT std_logic_vector(16 DOWNTO
0)); --1,16
END ENTITY synth_cordic;
ARCHITECTURE rtl OF synth_cordic IS
TYPE signed_array IS ARRAY (natural RANGE
<> ) OF signed(17 DOWNTO 0);
--ARCTAN Array format 1,16 in radians
CONSTANT tan_array : signed_array(0 TO 16)
:= (to_signed(51471,18),
to_signed(30385,18),
to_signed(16054,18),to_signed(8149,18),
to_signed(4090,18), to_signed(2047,18),
to_signed(1023,18), to_signed(511,18),
to_signed(255,18), to_signed(127,18),
to_signed(63,18), to_signed(31,18),
to_signed(15,18),
to_signed(7,18),to_signed(3,18),
to_signed(1,18), to_signed(0, 18));
SIGNAL x_array : signed_array(0 TO 14) :=
(OTHERS => (OTHERS =>'0'));
SIGNAL y_array : signed_array(0 TO 14) :=
(OTHERS => (OTHERS =>'0'));
SIGNAL z_array : signed_array(0 TO 14) :=
(OTHERS => (OTHERS =>'0'));
BEGIN
--convert inputs into signed format
PROCESS(resetn, clk)
BEGIN
IF resetn = '0' THEN
x_array <= (OTHERS => (OTHERS =>
'0'));
z_array <= (OTHERS => (OTHERS =>
'0'));
y_array <= (OTHERS => (OTHERS =>
'0'));
ELSIF rising_edge(clk) THEN
IF signed(z_ip)< to_signed(0,18)
THEN
x_array(x_array'low) <=
signed(x_ip) + signed('0' & y_ip);
y_array(y_array'low) <=
signed(y_ip) - signed('0' & x_ip);
z_array(z_array'low) <=
signed(z_ip) + tan_array(0);
ELSE
x_array(x_array'low) <=
signed(x_ip) - signed('0' & y_ip);
y_array(y_array'low) <=
signed(y_ip) + signed('0' & x_ip);
z_array(z_array'low) <=
signed(z_ip) - tan_array(0);
END IF;
FOR i IN 1 TO 14 LOOP
IF z_array(i-1) < to_signed(0,17)
THEN
x_array(i) <= x_array(i-1) +
(y_array(i-1)/2**i);
y_array(i) <= y_array(i-1) -
(x_array(i-1)/2**i);
z_array(i) <= z_array(i-1) +
tan_array(i);
ELSE
x_array(i) <= x_array(i-1) -
(y_array(i-1)/2**i);
y_array(i) <= y_array(i-1) +
(x_array(i-1)/2**i);
z_array(i) <= z_array(i-1) -
tan_array(i);
END IF;
END LOOP;
END IF;
END PROCESS;
cos_op <=
std_logic_vector(x_array(x_array'high)(16
DOWNTO 0));
sin_op <=
std_logic_vector(y_array(y_array'high)(16
DOWNTO 0));
END ARCHITECTURE rtl;
在 FPGA 中實現 CORDIC 有兩種基礎拓撲,一種是狀態機法,一種是流水線法。
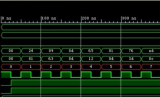
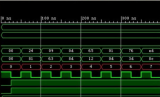
如果對處理時間要求不是特別嚴格,可以使用狀態機實現該算法,每周期計算一次 CORDIC 迭代,直到完成要求的周期次數。如果需要高計算速度,并行架構則更合適。上述代碼采用15 級并行旋轉模式 CORDIC 計算。它使用如表 2 所示的簡單圓函數模式 ArtTan(2-i) 查找表,結合簡單的陣列結構實現并行級。
在五花八門的各種方法中,CORDIC 算法證明自己是一種簡單且功能強大的算法,值得所有 FPGA 設計人員關注。更值得一提的是,使用內核生成工具或手動編碼可以輕松實現 CORDIC。
 電子發燒友App
電子發燒友App
























評論