1. 概述
基于FPGA實現各種設計的首要前提是理解并掌握數字的表示方法,計算機中的數字表示方法有兩種:定點數表示法和浮點數表示方法。其中,對于浮點數盡管當前應用最為廣泛的是基于IEEE 754所設計的浮點數表示方法,Xilinx(忘記Altera中是否有對應的IP核)的IP核中也提供了相應的設計方法,但其表示方法缺乏FPGA設計應有的靈活性,而且資源消耗相對嚴重,因此可以根據應用的需要,設計好基于FPGA實現的自定義浮點數。
2. 定點數表示
定點數大類上可分為有符號數和無符號數,需要清楚的是,無論是計算機還是FPGA,其底層并沒有無符號數、有符號數的概念,底層只是一大串二進制數據在進行運算(在底層就是一大堆寄存器處于開關的工作狀態中)。定點數的第一印象容易給人產生是用來表示整數的印象,然而無論是整數還是小數都可以采用定點數來表示,同理整數和小數的概念也是人為規定上去的,FPGA本身不會理解那一大串二進制數是表示整數還是小數,具體的運算法則由編程人員規定好。
1.1 Qm.n的表示方法
本文采用最廣泛使用的補碼表示形式(默認都懂其他的原碼表示和反碼表示形式),對應的用來表示有符號數。人為定義小數點的位置。
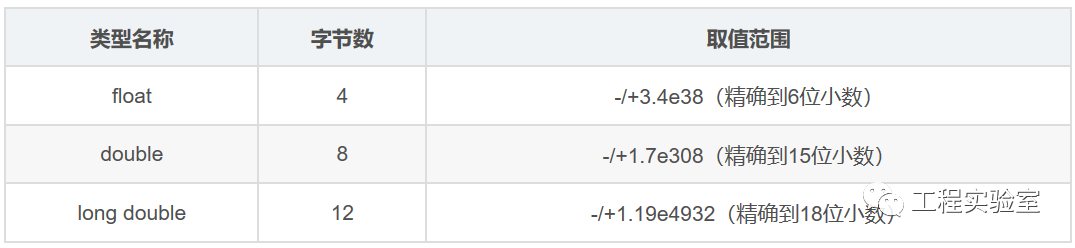
采用Qm.n量化表示定點數,其中m用來表示小數點前的位寬,包括一位符號位和m-1位整數位,n表示小數位寬。如16位有符號整數可以表示成Q16.0,用來表示小于1的小數則可以表示成Q1.15。對于Qm.n的表示格式,其范圍表示如下:
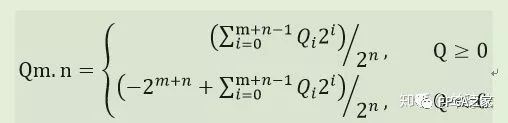
例如,1110整數則表示為Q4.0:(-2^4 + 2^3 + 2^2 +0)/2^0= -2,1110有兩位小數則表示為Q2.2:(-2^4+2^3+2^1+0)/2^2 = -0.5。下表對應表示16位二進制補碼表示的數的范圍。
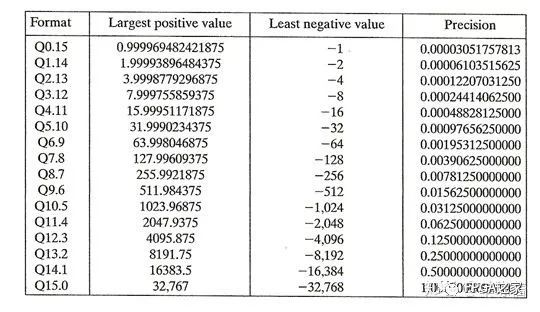
1.1 浮點數的定點化
浮點數的定點化涉及到量化方法。量化的過程可以表示為:
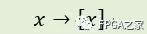
量化方法主要有兩種:尾部截斷舍棄法和尾部四舍五入法。
對于尾部截斷舍棄法,顧名思義則是丟棄掉尾部不能表示的部分。假設將浮點數表示成8位Q3.5的定點數,則表示過程如下(對3.2和-3.2進行定點化):
[3.2] = floor(3.2*2^5) = floor(102.4) = 102 = 01100110
[-3.2] = floor(-3.2*2^5) = floor(-102.4) = -103 = 10011001
采用MATLAB可以做如下實現:
dec2bin(floor(3.2*2^5), 8) = 01100110
dec2bin(2^8+floor(-3.2*2^5), 8) = 10011001
對于四舍五入法,則對應的過程表示如下:
[3.2] = round(3.2*2^5) = round(102.4) =102 = 01100110
[-3.2]=round(-3.2*2^5) = round(-102.4)= -102 = 10011010
采用MATLAB可以做如下實現:
dec2bin(round(3.2*2^5), 8) = 01100110
dec2bin(2^8+round(-3.2*2^5), 8) = 10011010
由于采用四舍五入方法還需要進行尾部數據的判斷,因此通常使用中,如無特別需求,多采用尾部截斷舍棄法。
3. 浮點數表示
在FPGA運算中,浮點數無論是表示方法、資源占用還是運算法則都比定點數復雜得多。但另一方面,基于FGPA 的實現的算法性能嚴重依賴于算法的數值精度表示,很多時候在信號處理中,數值的動態范圍過大,采用一般的定點算法往往無法滿足這樣大的動態范圍,而且定點算法經過精打細算之后,算法的小數位和整數位是固定的,表示的范圍同樣是固定的,無法在作調節,后續一旦有所修改,整個算法實現過程需要重新進行計算仿真設計,這樣的后期維護成本太高,簡直是牽一發而動全身。對于cpu處理器來說,浮點格式基本上會采用IEEE 754制定的標準單精度或雙精度格式。而對于FPGA來說,由于其強大的靈活性,雖然也是按照IEEE 754標準實現浮點數表示,但是卻可以對尾數和指數的位寬作修改。
IEEE 754定制的浮點格式在存儲方面有著很完美的形式,可以最大限度表示數的動態范圍的同時,減少存儲資源,但是實際參與運算時并沒那么直接,需要經過相應的換算。因此可利用FPGA的靈活性,自定義浮點數格式。
3.1 自定義浮點格式表示
不像根據IEEE 754[45] 標準所設計的32-bit和64-bit標準浮點格式,本論文的自定義浮點由位寬可配置的指數(Exponent)和尾數(Mantissa)兩部分組成。指數和尾數部分都是有符號定點數。作為一個例子,我們采用標準雙精度浮點格式和自定義浮點格式之間進行對比。標準雙精度浮點數可以表示如下等式:
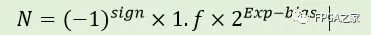
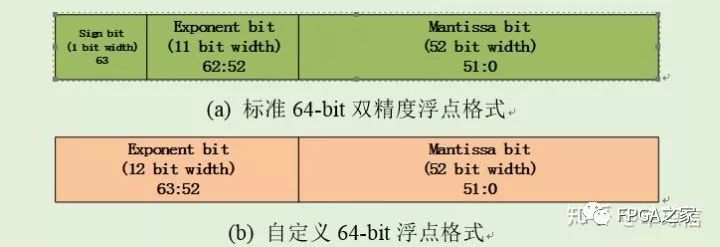
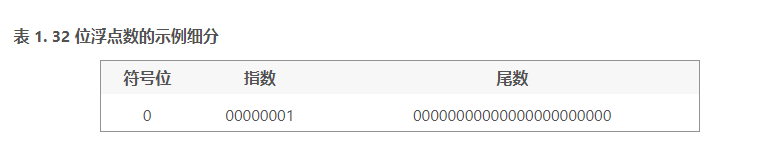
其中1.f表示52-bit尾數;Exp?表示存儲起來的指數值;bias?表示偏置,對于標準雙精度浮點,改值為1023;Exp-bias?表示實際的指數值。標準格式表示如圖(a) 所示。然而,對于自定義浮點格式表示的數的實際值如下:
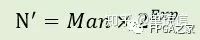
其中,Man?表示的尾數是52-bit有符號定點數,表示的實際值為0.1b49b48...b2b1b0 或者1.0b49b48...b2b1b0。而Exp?表示實際指數值。具體格式表示如圖(b)所示。
自定義浮點算法的其中一個優點是指數部分和尾數部分的位寬都是可配置的,設計者可以在算法精度要求和資源消耗方面進行權衡。而現存的由XILINX 提供的浮點運算IP 核是基于IEEE 754標準的,在每一次四則運算之后(如加法或乘法之后)都會進行一個格式化運算。而格式化運算占比的硬件資源消耗很大。無疑,如果存在多次連續加法運算或者乘加運算,這樣的運算方式是資源消耗嚴重的。而本文所提出的自定義浮點算法則是整合的乘加運算和連續加法運算,盡量減少格式化操作,從而減少資源消耗。
1.1 定點數轉自定義浮點格式
相比較于標準浮點格式的轉換,定點數轉成上文描述的自定義浮點格式相對來說簡單許多,只需要經過簡單的規格化,假設定點數為Qm.n,將其轉換為指數位寬為E,尾數位寬為M,其過程可以描述如下:
輸入:定點數Qm.n,則初始指數值為m,尾數Q1.(m+n-1);
規格化:計算符號位個數,假設計算得符號位個數為k;
輸出:指數輸出值為m-k,尾數從m+n-k作為最高位開始截位,截取M位,如果不夠長,則從最低位開始補零,補足到M位長度輸出。
這里唯一需要再次說明的是,如何計算符號位的個數,最簡單的方法就是采用一個for循環,for循環里邊使用一個計數器(初始值為1)和比較判斷器,從次高位開始與最高位做比較,如果相同(同為1或者同為0),則計數器加1,以此類推下去。這里使用MATLAB,按照比特級別仿真,打包成一個函數,如下:
?
function k = dupSign_cal(u)% ?u: 定點數輸入 % k:計算符號位個數 bit_len = get(u, 'WordLenght'); SignBit = bitget(u, bit_len); count = 1; for i = bit_len-1:-1:1 if bitget(u, i) == SignBit ? count = count+1; else ? break; end end
?
當然,無論是verilog里邊的for循環還是vhdl里邊的for循環,并非軟件中for的概念意義,實際上FPGA綜合時會將for循環全部展開,因此這里如果定點數太長,則for循環不但消耗的資源多,而且非常容易造成時序不過關(想想在規定的一個或兩個時鐘里邊完成幾十比特一比特一比特的比對)。因此如果定點位寬太長,則應該想更多的辦法來完成該過程,FPGA節省時間的方法無外乎增加資源,一個for循環不行,并行多個for循環嘛。
 電子發燒友App
電子發燒友App












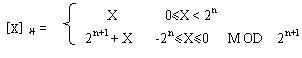


















評論