|作者：陳煥陽1，? 段琦琳1 伍瑞新2 馬紅孺3

(1 廈門大學物理科學與技術學院)

(2 南京大學電子科學與工程學院)

(3 云南大學物理與天文學院)

本文選自《物理》2022年第12期

摘要???基于變換光學的幻象光學器件能夠表現出自然界中不存在的現象，如隱身、超散射和隱形門等。其中電磁超散射現象利用變換光學中的折疊幾何變換，使得物體的散射截面遠大于其幾何截面，顛覆了人們對于傳統散射中散射截面通常小于散射體幾何截面的認知。這一現象也為現實中實現“穿墻術”提供了可能。文章著重介紹了基于變換光學的超散射的發展歷程以及利用超散射實現隱形門的方法。隱形門在自由空間的實現為將來幻象器件的設計提供了新的思路。

1??引言 ? ?

許多影視和文學作品中對于“隱身”的描繪令人心馳神往，其中最著名的當屬《哈利波特》中的隱身衣，當披上隱身衣即不為外部所見。人能感知到物體是由于接收到了物體反射的光，因此隱身的關鍵就是對于光的操縱。穿墻術在神話中指人作為主體具有穿過實體墻的超能力，現實中“穿墻”則需要通過改變墻的特殊光學性質來實現。對電磁波來說，穿墻術就是物體可以穿過一道特殊的門，而此門卻不為觀察者所見，即“隱形門”。用隱形門實現的穿墻術與幻象光學息息相關。物體的幻象光學效應是指被觀測到的物體和實際物體本身不同的一種光學現象，其中一個典型的例子是超散射效應，散射體的散射截面被極度增大[1]，即對觀察者而言物體的尺寸變得很大。2009年，上海交通大學馬紅孺/羅旭東課題組在研究中首先發現超散射。理論研究表明，超散射體可以用補償介質[2]結合變換光學的方法[3]加以實現。這一方法已被用來設計許多奇妙有趣的幻象光學器件，如基于超散射效應的隱形通道或隱形門[4]、超吸收體[5]、非包裹隱身衣[6]和內窺鏡[7]等，其中隱形門是最受關注的幻象光學器件。通過合理設計材料的介電常數ε?和磁導率μ?(或折射率n )，2009年研究人員首先在理論上實現了隱形門。然而，此隱形門對所需材料的折射率分布要求極其苛刻[4]，在實驗上很難實現。后來人們提出一種基于簡化參數的隱形門設計方案[8]，并用電路等效的方法驗證了隱形門的存在性[9]。然而直至2021年，真正的隱形門才在實驗上得到證實。南京大學伍瑞新課題組和陳煥陽合作，首次在微波頻率的自由空間中驗證了超散射現象，在實驗中實現了電磁隱形門這一幻象光學器件[10]。

隱形門從首次的理論提出到最終的實驗實現經歷了十余年。本文將著重介紹隱形門的發展歷程，主要從三個方面概述：首先是變換光學這一強有力理論的提出；其次是從準靜態極限到電磁超散射的提出；最后是基于超散射效應的隱形門理論設計以及實驗驗證。隱形門在實驗上的成功實現將為今后新型光場調控器件的應用和發展提供新的思路。

2? 變換光學 ? ?

光線在均勻介質中沿直線傳播，當光線通過兩個介質的交界面時會發生偏折。在生活中，放在盛有水的透明杯中的筷子仿佛被“折斷”就是這一原理的體現。當折射率出現漸變分布時，比如由于溫度的不均勻導致沙漠上空氣的密度不同從而產生漸變的折射率分布，進而出現神奇的海市蜃樓現象。這讓我們不禁想到，只要設計出具有一定折射率分布的介質，那么光線就會在其中沿著特定的方向傳播。

2006年，Pendry等[3]和Leonhardt[11]分別獨立地提出了通過變換光學設計隱身衣的方法。如圖1(a)所示，在“虛擬空間”，即真空中，光線沿著直線傳播，通過坐標變換，空間中的一個點膨脹開形成一個“物理空間”中的圓(圖1(b))，光線會繞著紅色圓圈傳播，因此紅色圓圈內部對外部不可見，呈現出隱形效果[12]。這一理論的提出讓《哈利波特》中神奇的隱身衣有了實現的可能。隨后，Smith等人利用開口諧振環作為超構材料的結構單元在微波波段的實驗上實現了單頻的二維隱身器件[13]。自此，變換光學因具有可自由操控光場的能力吸引了人們的廣泛關注。

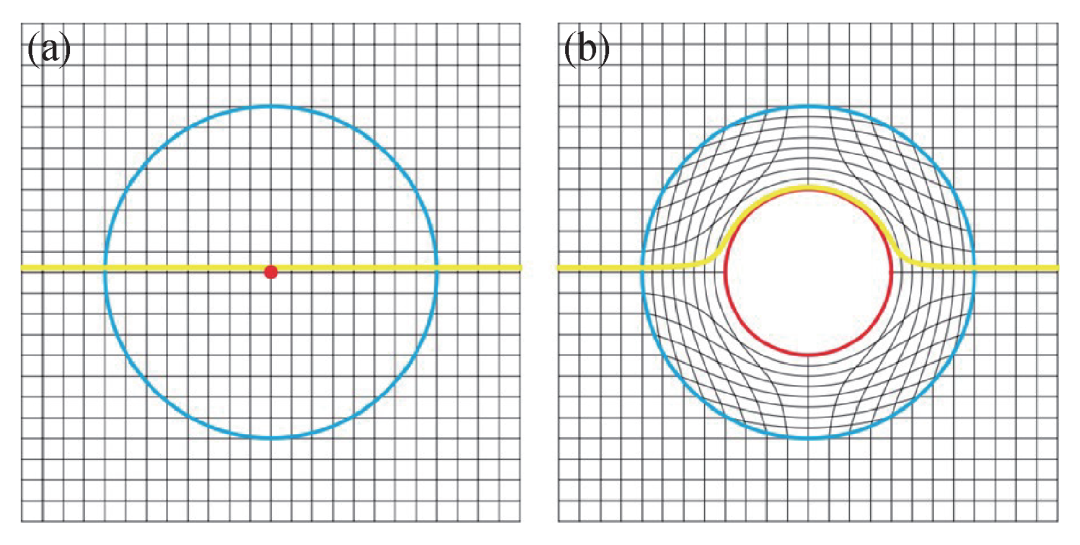
圖1 坐標變換? ?(a)變換前在自由空間沿直線傳播的光線；(b)通過變換將一個點膨脹成一個圓(紅色圓圈)，光線繞過圓形區域傳播[12]

變換光學的核心是通過坐標變換在兩個空間(虛擬空間和物理空間)建立起變換關系。由于坐標變換前后麥克斯韋方程組具有形式不變性，故兩個空間中的電磁參數(介電常數ε和磁導率μ)可以建立起與坐標變換的對應關系[14]：

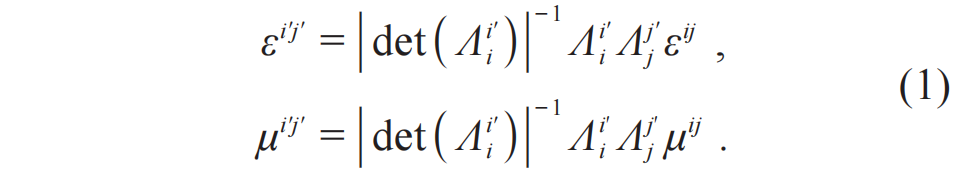
其中

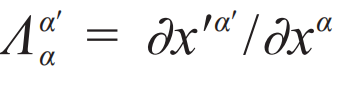
是虛擬空間與物理空間的雅可比變換矩陣，i、j?以及i?'、j '從1到3選值以分別表示三個空間坐標。利用變換光學可以設計出許多具有新穎功能的器件，如隱身衣[15]、旋轉衣[16，17]、匯聚器[18]以及幻象器件等。

圖2 部分幻象光學器件及其對應的坐標變換關系? ?(a)理想隱身衣；(b)弱化設計后的隱身衣；(c)基于法布里—珀羅共振的隱身衣；(d)折疊變換后的隱身器件；(e—h)相應器件對應虛擬空間r與物理空間r?′的變換關系，其中黃色圓點對應變換的轉變點，r與r?′分別表示變換前后同心圓環的半徑

變換光學自提出以來，最受關注的就是“隱身衣”的設計，如圖2(a)所示，隱身衣可以引導光線圍繞物體傳播，從而使物體“隱形”。在圓柱極坐標下，該理想二維隱身衣對應的變換關系如圖2(e)所示，即：

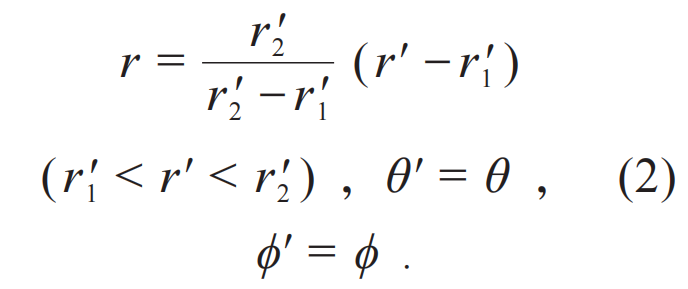
然而這樣的理想隱身衣只能在單一的頻點下工作，無法在較寬的頻率范圍內實現完美的隱身效果。針對這一問題，陳煥陽等提出了色散隱身衣[19]，這種隱身衣相較于理想隱身衣工作頻率有所拓寬，但伴隨著部分性能的犧牲。色散隱身衣設計的核心思想是用一個更一般的變換形式，如圖2(f)所示，將一個共心圓環區域區域r0?

2015年，陳煥陽/侯波課題組將法布里—珀羅共振引入了變換光學器件的設計中[20]，這樣的器件可以在多個共振頻率下工作，使得變換光學器件的多頻率應用成為可能。如圖2(g)所示，其變換的核心是將虛擬空間中的r1?≤?r?

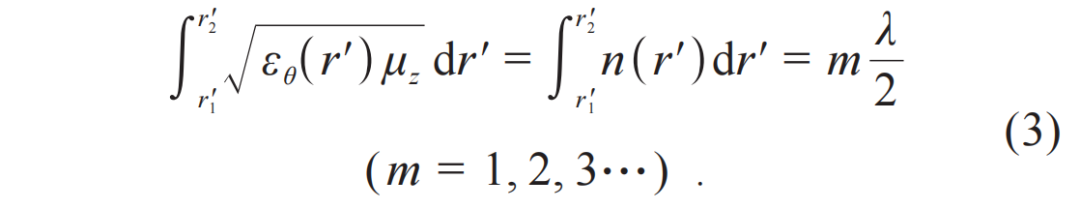
當m?= 3，r2′?= 2，r1′?= 1時，εθ(r′) = (3 -?r?′)2，其電磁波分布如圖2(c)所示，并且這一器件在實驗上得到了驗證。

當變換選擇的標記點位置進一步抬高，則對應折疊幾何變換。與之前提到的三種變換不同的是，如圖2(h)所示的折疊變換由于斜率為負將會引入負折射率材料(ε<0，μ<0)[21，22]。負折射率材料在自然界中并不存在，但是可以通過人工超構材料構造出ε?和μ?同時為負的負折射率材料[23，24]。在負折射率材料中，光的傳播與其在傳統材料中的傳播特性相反，從而引發許多“違背常理”的光學現象，為人們操控光的傳播提供了更多的可能。其中最著名的應用是Pendry提出的可以實現超越衍射極限的完美成像效果[22]。這一成像過程在幾何光學方面，可以從變換光學的角度來看，將其理解為空間的折疊變換，由虛擬空間中的單個點對應于物理空間中的三個點[25]。早在2003年，Pendry基于負折射率平板提出了補償介質的概念[2]，補償介質由兩個具有相反電磁特性的區域構成，光在通過補償介質后沒有相位的積累，看起來仿佛這一塊區域不存在[26]。在圖2(d)中，由內向外三個圓的材料依次是均勻介質(r?

結合負折射率和補償介質還可以設計出許多有趣的幻象光學器件。賴耘等人提出了非包裹式的隱身[6]，其原理是利用補償介質來消除被隱物體的反射以實現隱身效果。這不同于圖2(a)中的隱身裝置，由于光線無法進入r = r1′內部，故圖2(a)中隱身裝置內部的觀測者是看不到外部情況的，而非包裹式隱身內部的觀測者可以看到外部情況。通過折疊幾何變換還可以設計出反隱身的器件，破壞由正折射率材料組成的隱身器件的隱身效果[27]。這些神奇的幻象器件不禁讓人思考，所見即是真實嗎？

3??電磁超散射的提出與發展 ? ?

電磁波入射到物體表面時會發生散射，電磁散射是非常普遍的物理現象[28]。例如，晴朗的天空呈現藍色源于瑞利散射：空氣中的分子尺寸遠小于光的波長，可見光中藍光波長較短因此更容易發生散射，這就是蔚藍天空所蘊含的物理奧妙。當空氣中存在較多比光波長尺寸大的塵粒和液滴時會發生米氏散射，米氏散射中所有波長的光均等散射，故而天空呈灰白色。電磁散射還具有許多重要的應用。例如，在通信領域中，可以利用對流層對電磁波產生的散射作用進行超視距通信；在軍事雷達探測中，通過分析散射特征可以得到散射物體的信息。

可以看到在傳統散射中，散射特征與散射體尺寸息息相關，物體的散射截面通常小于其幾何截面。普通材料對于電磁波的調控能力有限，即便是相較于波長尺寸較大的散射體，其散射截面僅趨近幾何截面。一些基于共振效應獲得的超出幾何截面的散射截面，也可以通過分析各級米氏散射系數，將其與非共振散射體區分出來。變換光學和超材料的出現，極大增強了人們對電磁場的操控能力，除了可以完美消除散射的隱身效應，還可以使小物體與大物體的散射特征無法區分，即“超散射”現象。這一現象顛覆了電動力學中大尺度物體最大散射截面是其幾何截面的傳統認知。

超散射通過增強散射截面使得一個物體看起來比其實際尺寸大。該現象在傳感[29]、匯聚能量[30，31]、熒光成像[32]、電力無線傳輸[33]等方面有廣泛的應用前景。考慮從如圖3(a)所示核層結構的散射問題出發，在準靜態極限下(即物體尺寸遠小于波長)，可以使用近似的麥克斯韋方程組來求解問題，并且可以忽略其他項而只考慮偶極子項[34]，分析芯層(ε1)、殼層(ε2)和背景材料(ε3)組成的物體對于以離散電偶極子為源的響應[35]。當ε1+ε2=0且ε2+ε3=0時，物體對于外部場沒有影響；而僅當ε2+ε3=0時，芯層的散射會超過殼層的散射，仿佛芯層的半徑被放大。在準靜態極限下可以產生芯層被放大的現象，從準靜態極限過渡到電磁散射(需要考慮其他階數項的散射)。目前主要有三種方法可以實現超散射：第一種是通過變換光學的方法，并引入補償介質的概念來放大物體，從而實現超散射[1]；第二種是利用多層金屬—介質亞波長納米柱表面等離激元的共振打破單通道散射極限，以此實現超散射現象[36，37]，該方法通過共振只能實現有限階數的放大，并且材料的損耗對散射增強效果影響很大；第三種是利用近零折射率材料來增強物體散射[38，39]，該方法需要近零折射率的背景環境，對制備和兼容性提出了進一步的挑戰。本文聚焦于第一種實現超散射的方法，下面將做進一步的介紹。

在準靜態條件下，低階散射系數起到決定性作用，當物體的尺寸與波長可比擬時，不能忽略高階散射，通過變換光學的手段可以實現具有與波長可比擬尺寸的物體的超散射[1]。從圖3(b)的負折射率平板出發，在小于負折射率平板(黃色區域)厚度的位置放置點源S，通過幾何光學可知點源S會在F2和F1處成像。在R1處設置完美電導體邊界(PEC)，光線會被反彈回來，而區域R2?

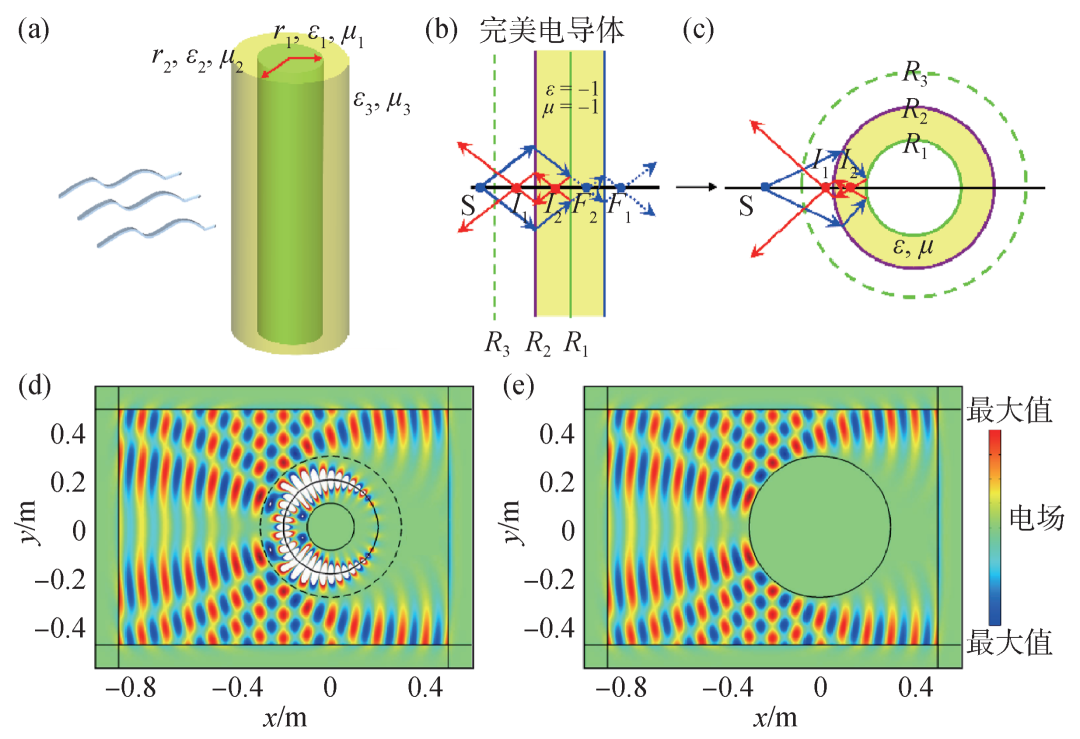
圖3 (a)核層結構的電磁散射示意圖；光線在平板負折射率材料(b)與圓柱負折射率材料(c)中的傳播，其中綠色實線為完美電導體[1]；(d)內外半徑分別為R1=0.1 m與R2=0.2 m的超散射圓柱周圍的總電場分布[1]；(e)半徑R3=0.3 m的完美電導體的總電場分布，(d)，(e)均為平面波入射[1]

當頻率為3 GHz的橫電模式(電場沿著z方向)平面波入射時，圖3(d)，(e)的電場分布相同，證明了超散射現象。其背后的物理機制是負折射率殼層對于倏逝波的放大。這種超散射現象不僅可以放大圓柱形狀的物體，也被證明了可以放大其他形狀的物體[26，40]。

4??電磁隱形門的實現 ? ? 在電影《哈利波特》中，站臺是登上霍格沃茨特快列車的隱形通道(或隱形門)，如圖4(a)所示，這既是魔法，也可以是一種幻象光學效應，即這個通道在空間上是實際存在的，但是在通道外的觀察者卻無法從視覺層面看到。隨著變換光學的不斷發展，研究人員發現結合超散射技術，便可實現隱形通道效應。

2009年，上海交通大學馬紅孺/羅旭東課題組[4]進一步發展了圖3(d)中提出的超散射體，將其推廣為方形超散射體并置于兩個恰當距離的金屬墻體之間。如圖4(b)所示，其中完美電導體的高度為2b3，隱形通道的區域寬度設計為2a3。當|x| ≤?a3+δ區域不存在超散射體時，則此通道區域( |x| ≤?a3+δ?)顯然可以通過分析散射電磁波被探測到，而當在該通道區域中放置設計好的方形超散射體時(該超散射體為Γ2邊界面包圍的區域)，由于該超散射體散射截面大于其幾何截面，故電磁波無法通過，因此構造了一個“隱形”通道。他們利用COMSOL仿真展示了當入射光源位于隱形門一側時，觀察者在隱形通道兩側時會看到截然不同的“景象”，如圖4(d)，(e)所示。這樣的隱形門設計雖與實際場景相符合，但實現起來需要負折射率材料，并且對材料的折射率分布要求苛刻，限制了隱形通道器件的發展。

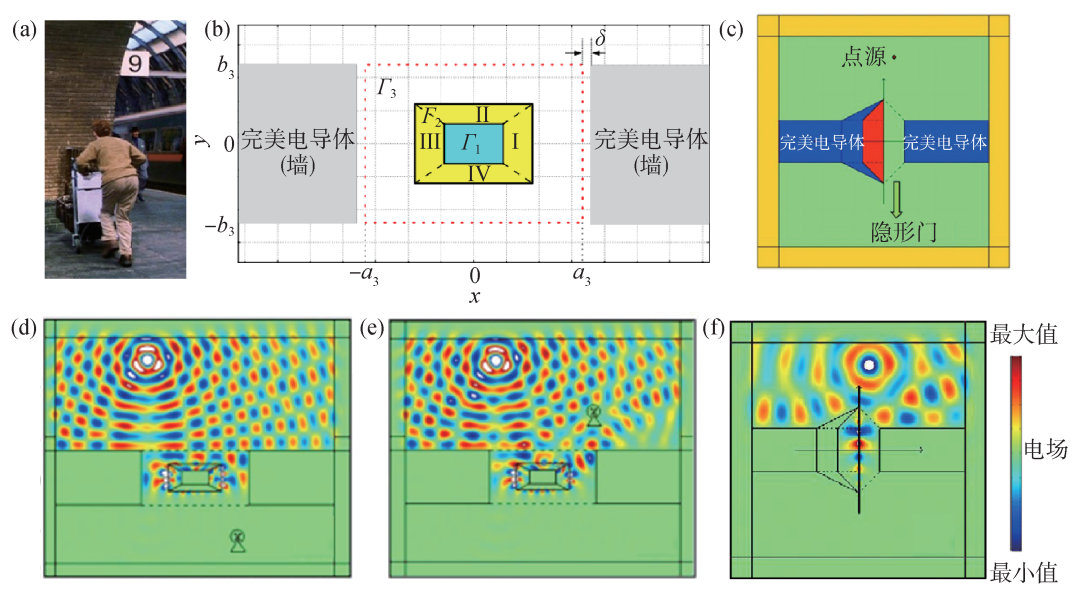
圖4 隱形門的理論原型設計[4，8]? ?(a)《哈利波特》中的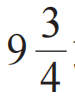站臺；(b)一種包裹式的隱形門，其中Γ1為完美電導體區域，Γ2為負折射率包裹區域，Γ3為電磁波無法透過的區域；(c)一種簡單化的隱形門；(d)，(e)對應(b)中的隱形門，通過仿真演示了觀察者分別位于兩側的效果；(f)對應(c)中的隱形門效果

同年，陳煥陽等[8]提出一種簡化的隱形門原型設計，如圖4(c)所示。這種新的超散射體不再需要復雜折射率分布的材料，取而代之的是填充部分折射率為-1的材料，并且還具有一定的工作帶寬。在光源激勵下，由于負折射率材料的存在(圖4(c)中的紅色區域)，會在空氣和材料界面激發表面波，進而表現出超散射的現象，其散射截面等效于器件本身附加填充負折射率材料區域的鏡像部分。在考慮橫電模式的情況下，在超散射體兩端放置完美電導體，自然形成了隱形通道。如圖COMSOL仿真結果4(f)所示，一側的電磁波在通過器件的空氣通道時被完美“阻擋”，但卻可以讓物體通過，充當著完美的隱形門。此外，他們還給出了利用磁光子晶體來實現隱形門的方案，并進行了仿真驗證。

在隱形門簡易化原型提出后不久，研究者們便利用電路模擬方法在實驗中予以實現。2010年，中國科學院電子學研究所李超和陳煥陽等人合作，利用傳輸線模型，在實驗中首次模擬驗證了隱形門器件[9]。如圖5(a)所示，他們利用串聯電感和并聯電容來模擬空氣，利用串聯電容和并聯電感來模擬負折射率材料，并優化兩者的邊界，最后在電路板上構造了隱形門器件，通過圖5(b)的實驗測量結果可以看出，隱形門可以完美阻擋交流信號的傳播。

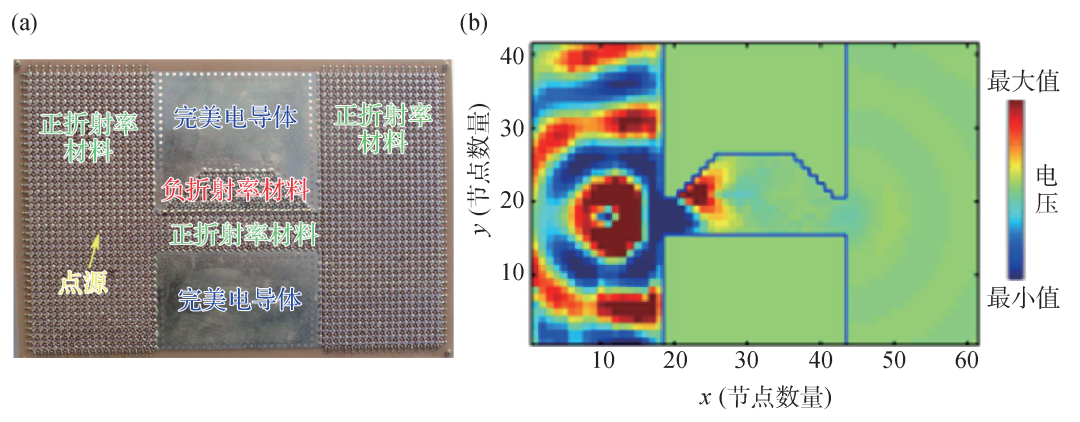
圖5?隱形門的電路實驗實現[9]? ??(a)利用電路模型模擬的隱形門器件；(b)電路模擬隱形門實驗測量結果

電路模擬的驗證方法為幻象光學器件的實現提供了一個可行方案，然而這與真實的場景仍有天壤之別，人們期待在真實環境中實現真正的隱形門。直到2021年，南京大學伍瑞新課題組與陳煥陽合作[10]，采用簡化的隱形門設計方案[8]，利用自偏置鍶磁鐵氧體陣列構建超散射體，并在自由空間中搭建了隱形門，如圖6(a)所示。在實驗中首次直接觀測到空氣通道對電磁場有著顯著的阻斷作用，如圖6(b)所示，入射電磁波沿著通道迅速衰減，在空氣通道的盡頭電場幾乎消失，從而實現了自由空間中真實的隱形門。作為對比，如圖6(c)所示，置于兩完美電導體之間與圖6(c)具有相同寬度的空氣通道則無法阻擋電磁波的傳播，入射電磁波可以穿透空氣通道而沒有衰減。為了進一步說明該隱形門對電磁波的阻擋效果，圖6(d)展示了在圖6(a)中標記的從B點到B′點的歸一化電場能量密度，可以看到在隱形門中，電場能量密度迅速衰減，從B點到B′點有90%的能量被阻擋，而在金屬波導中電場能量密度的衰減僅為15%。圖6(e)則展示了在實驗中隱形門和金屬波導兩個端口的電場能量密度比值與頻率的關系，可以看到在綠色陰影區間內比值逐漸減小而對應的金屬波導的比值則較為穩定。綜上說明了該隱形門對電磁波傳播的阻擋能力。超構材料隱形門的實現進一步推動了幻象光學器件的發展，使得隱形門在真實場景中的應用成為可能。

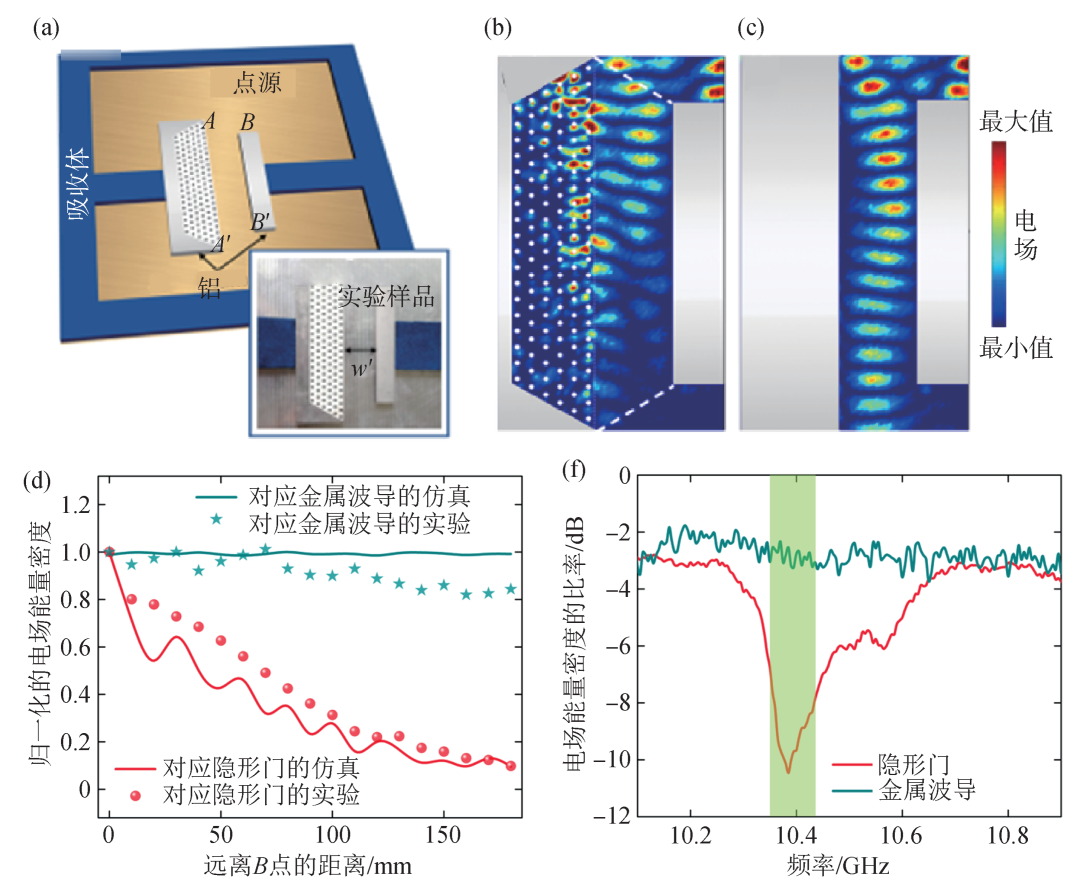
圖6 隱形門在微波頻段的自由空間的實驗實現[10]? ?(a)利用鐵氧體陣列(白色梯形陣列區域)搭建的電磁隱形門器件，與鐵氧體陣列接合的金屬鋁作為完美電導體；(b)電磁隱形門實驗測量結果；(c)用完美電導體代替鐵氧體陣列實驗對比結果，在圖(b)，(c)中，鐵氧體用白點標記，鋁用灰色表示；(d)實驗與仿真中沿著隱形門(對應(b)圖)和金屬波導(對應(c)圖)的空氣通道的歸一化的電場能量密度；(g)實驗中隱形門與金屬波導在輸出端口與輸入端口處的電場能量密度比值與頻率的關系

5? 總結 ? ?

一直以來，自由操控電磁波是人們孜孜不倦的追求。應用變換光學使得人們可以通過設計材料的電磁參數實現對電磁波散射的調控。當散射被抑制時可以實現完美的隱身衣，當散射被放大時就可以實現超散射現象。超散射不僅在傳感、能量收集等領域有廣闊的應用前景，而且還可以用于構造如隱形門等光學幻象器件。隱形門從最開始的電路等效實驗到微波頻段的自由空間中的實驗實現，預示著幻象光學領域又前進了一大步。值得注意的是，由于材料參數的簡化，該隱形門器件的橫向和縱向電尺寸(物理尺寸/波長)無嚴格的限制(橫向電尺寸通常大于1，縱向電尺寸通常大于2)，并且可以拓寬到其他光學頻段，例如可見光、紅外波段等。然而目前隱形門的實現主要依賴負折射率材料(折射率n=-1)，因此在工作帶寬上存在一定的限制，且不能推廣到幾何光學領域。隨著聲學負折射率材料的提出，該隱形門今后有望推廣到三維聲學領域中用于聲波的調控。

致 謝??有許多合作者都對這一系列工作做出了極大的貢獻和影響，不能一一羅列。比如，香港科技大學的陳子亭教授，張昭慶教授和沈平教授，上海交通大學的羅旭東教授和寧夏大學的楊濤教授，南京大學的賴耘教授，蘇州大學的侯波教授和徐亞東教授，南方科技大學的吳紫輝教授，復旦大學的林志方教授和浙江師范大學的劉士陽等，和他們在一起的討論，是極其愉悅的回憶，也是人生的幸事！還要感謝廈門大學的博士生殷玉杭、趙鵬飛、朱杉的辛勤工作與校正。

參考文獻

[1] Yang T，Chen H，Luo X et al. Opt. Express，2008，16：18545

[2] Pendry J B，Ramakrishna S A. J. Phys-Condens. Mat.，2003，15：6345

[3] Pendry J B，Schurig D，Smith D R. Science，2006，312：1780

[4] Luo X，Yang T，Gu Y et al. Appl. Phys. Lett.，2009，94：223513

[5] Ng J，Chen H，Chan C T. Opt. Lett.，2009，34：644

[6] Lai Y，Chen H，Zhang Z Q et al. Phys. Rev. Lett.，2009，102：093901

[7] Lai Y，Ng J，Chen H et al. Phys. Rev. Lett.，2009，102：253902

[8] Chen H，Chan C T，Liu S et al. New J. Phys.，2009，11：083012

[9] Li C，Meng X，Liu X et al. Phys. Rev. Lett.，2010，105：233906

[10] Ye K P，Pei W J，Sa Z H et al. Phys. Rev. Lett.，2021，126：227403

[11] Leonhardt U. Science，2006，312：1777

[12] Leonhardt U，Tyc T. Science，2009，323：110

[13] Schurig D，Mock J J，Justice B et al. Science，2006，314：977

[14] Pendry J B，Aubry A，Smith D et al. Science，2012，337：549

[15] Cummer S A，Popa B I，Schurig D et al. Phys. Rev. E，2006，74：036621

[16] Chen H，Chan C T. Appl. Phys. Lett.，2007，90：241105

[17] Chen H，Hou B，Chen S et al. Phys. Rev. Lett.，2009，102：183903

[18] Sadeghi M M，Xu L，Nadgaran H et al. Sci. Rep.，2015，5：1

[19] Chen H，Liang Z，Yao P et al. Phys. Rev. B，2007，76：241104

[20] Sadeghi M，Li S，Xu L et al. Sci. Rep.，2015，5：1

[21] Veselago V G. Sov. Phys. Usp.，1968，10：509

[22] Pendry J B，Phys. Rev. Lett.，2000，85：3966

[23] Smith D R，Pendry J B，Wiltshire M C. Science，2004，305：788

[24] Shalaev V M. Nat. Photon.，2007，1：41

[25] Leonhardt U，Philbin T G. New J. Phys.，2006，8：247

[26] Chen H，Chan C T，Sheng P. Nat. Mater.，2010，9：387

[27] Chen H，Luo X，Ma H et al. Opt. Express，2008，16：14603

[28] Kerker M. The Scattering of Light. New York：Academic press，1969

[29] Wan W，Zheng W，Chen Y et al. Nanoscale，2014，6：9093

[30] Schuller J A，Barnard E S，Cai W et al. Nat. Mater.，2010，9：193

[31] Green M A，Pillai S. Nat. Photon.，2012，6：130

[32] Kinkhabwala A，Yu Z，Fan S et al. Nat. Photon.，2009，3：654

[33] Zhu L，Luo X，Ma H. Appl. Phys. Lett.，2016，109：024103

[34] Alù A，Engheta N. J. Nanophotonics，2010，4：041590

[35] Nicorovici N，McPhedran R C，Milton G W. Phys. Rev. B，1994，49：8479

[36] Ruan Z，Fan S. Phys. Rev. Lett.，2010，105：013901

[37] Qian C，Yang Y，Xiong X et al. Phys. Rev. Lett.，2019，122：063901

[38] Zhou M，Shi L，Zi J et al. Phys. Rev. Lett.，2015，115：023903

[39] Zhou M，Ying L，Lu L et al. Nat. Commun.，2017，8：1388

[40] Pendry J B. Nature，2009，460：579

編輯：黃飛

?