本文討論了一些重要的FFT特性,解釋了如何利用這些特性設置FFT以實現高效的分析。
快速傅里葉變換(FFT)是20世紀70年代微處理器進入商業設計時首次出現的。從昂貴的實驗室型號到最便宜的業余型號,現在幾乎每一臺示波器都能提供FFT分析功能。FFT是一種功能強大的工具,高效使用FFT要求人們對FFT有一定的研究。本文將介紹如何設置FFT和高效使用FFT,FFT的技術原理這里不再贅述。
FFT是一種能夠縮短離散傅里葉變換(DFT)計算時間的算法,也是一種用于在頻域(幅度和相位與頻率的關系)中查看所采集的時域(幅度與時間)數據的分析工具。FFT給數字示波器增加了頻譜分析功能。
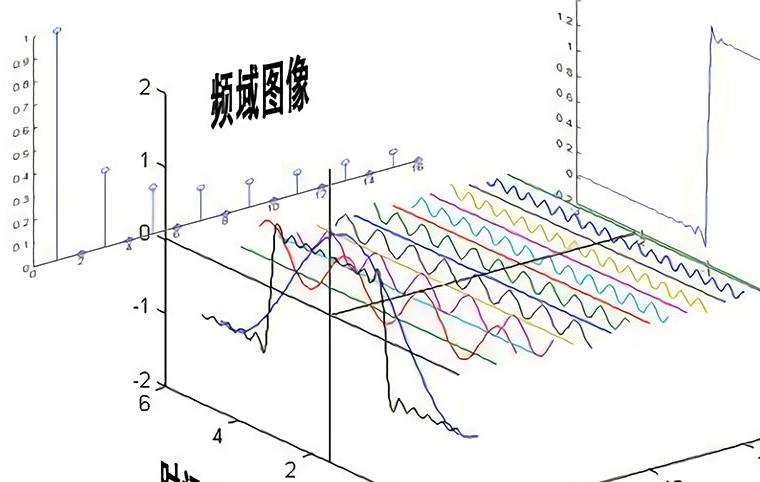
觀察圖1中的上半部分曲線,你看到的是一個經過幅度調制的載波,它使用梯形脈沖作為調制函數。在看圖1中的這個時域圖時,如果讓你告訴我信號的帶寬,你可能一時答不上來。但如果你對這個信號進行FFT處理,就能得到另外一個視角。這個信號有一個線性掃描的頻率,帶寬用光標標記出來了,是4.7MHz。這正是示波器中增加FFT功能的原理,它是從另外一個角度來看同樣的數據。
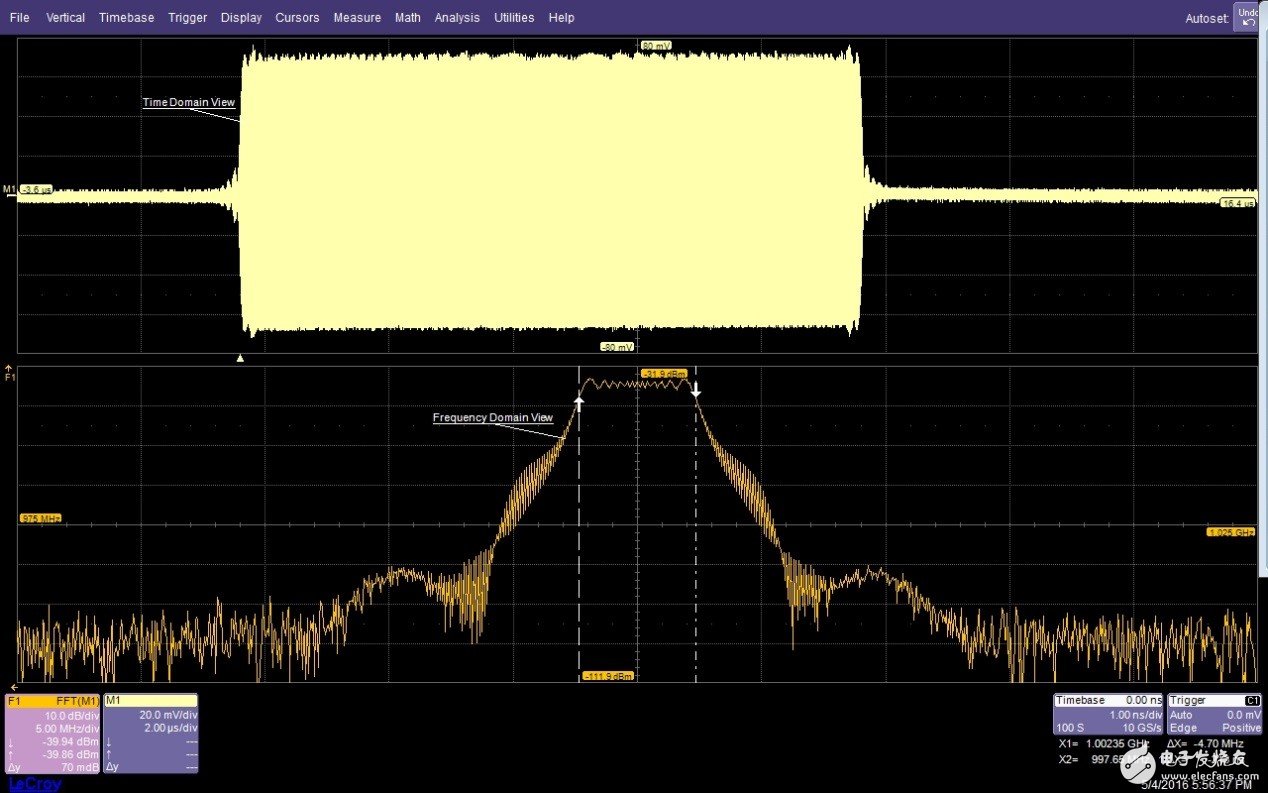
圖1:上面的時域圖顯示了脈沖調制的射頻載波,下方的頻域圖顯示了在997MHz和1002MHz之間均勻分布的載頻
FFT頻帶寬度和分辨率帶寬
在最早的電路課程中,你應該學過周期信號的頻率(頻域)是周期(時域)的倒數。同樣,這個關系貫穿在整個FFT設置過程中。
設置FFT最好從選擇分辨率帶寬(RBW)開始,因為它與單參調整有關。RBW (Δf)是顯示FFT頻率軸的增量步距。在時域中,采樣周期決定了樣本之間的時間間隔。而在頻域中,RBW是頻譜圖中相鄰“單元”之間的頻率差值。RBW是時域記錄長度(也稱為采集時間)的倒數,如圖2所示。你可以用示波器的水平刻度或時間/格參數設置來控制RBW。圖1中的采集時長是20μs,頻譜圖中的RBW是它的倒數,即50kHz。
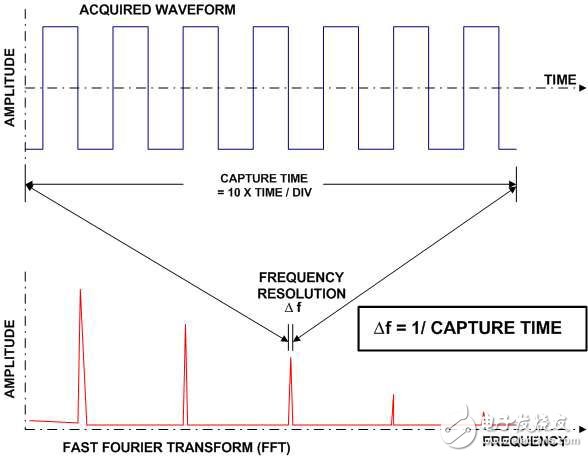
圖2:頻譜的分辨率帶寬是時域記錄長度或采集時間的倒數
設置FFT的下一步是確定頻域圖的寬度——FFT中最高頻率和最低頻率之差。注意,FFT通常從0 Hz開始,一直到整個頻帶寬度。這與射頻頻譜分析儀有很大的區別,馬上我會講到。
FFT的頻帶寬度是示波器有效采樣率的一半(圖3)。時域中的最短時間增量——采樣周期——決定了頻域中的最大分量。同樣,頻域中的最小增量是時間記錄中最長持續時間的函數。這符合時域和頻域之間的倒數關系。
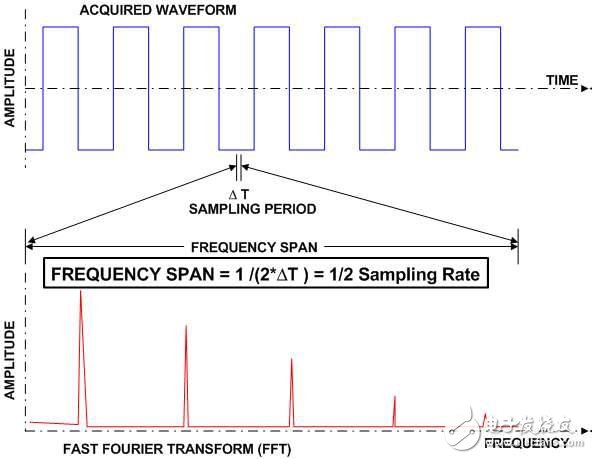
圖3:頻譜寬度是示波器有效采樣率的一半
為了在頻域中取得更高的分辨率,必須增加采集的數據量,方法是增加時間/格設置值。這與在示波器的時域圖中增加時間分辨率的做法剛好是相反的。
從實用的角度看,時域記錄長度是由示波器的時間/格參數值控制的。一旦你選擇了時間/格參數值來達到想要的分辨率帶寬,那么控制采樣率達到所需頻帶寬度的唯一方法是修改示波器的采集內存長度。現在事情似乎復雜起來了,確實是這樣。
最近,大多數高端示波器制造商都修改了FFT用戶界面,使它更類似于標準的射頻頻譜分析儀,設置中心頻率和頻帶寬度時將分辨率帶寬作為一個參數。雖然這類界面使得FFT使用起來更容易,但確實隱藏了FFT的基本功能,導致必須接受示波器設置的時間/格、采樣率和內存長度組合。根據這部分討論的一些規則,你可以手工設置FFT,并在設置中獲得更多的自由度。
垂直縮放
根據示波器的不同,FFT也許可以選擇垂直刻度,也許只能是固定的單一垂直格式。最常見的垂直格式是功率譜,它以功率為單位顯示垂直幅度,常用相對于1毫瓦的分貝表示(dBm),并在對數垂直刻度上顯示。這種選擇也是射頻頻譜分析儀功能的保留。實驗室級別的示波器可以提供更多的數據,包括功率譜密度(PSD)、線性幅度、平方幅度、相位或實數/虛數分量。
PSD是歸一化為FFT分辨率帶寬的功率譜值。它的測量單位是dBm/Hz,代表單位帶寬上的功率。PSD在測量寬帶現象(如噪聲)時非常有用。幅度格式顯示示波器測量的線性單位的頻譜幅度,如伏特(V)或安培(A)。
幅度平方顯示顧名思義是將頻譜幅值顯示為幅度的平方值,單位可以是V2、A2等等,并且在歸一化為儀器輸入阻抗(通常是50Ω)時為功率測量提供線性縮放。歸一化是利用示波器的再縮放函數實現的,它允許乘以一個常數。對于50Ω來說,幅度平方譜乘以0.02(即1/50),即對于50Ω輸入阻抗而言將單位改為瓦(V2/50)。
從數學的角度來看FFT頻譜是一個復雜函數,幅值的顯示只是全貌的一半。FFT輸出由實數和虛數部分組成,一些示波器可以同時顯示這兩部分。作為實數分量和虛數分量的替代,許多示波器顯示FFT相位和幅值。這兩個成對的輸出格式(實數/虛數和幅值/相位)構成了完整的FFT。計算反向FFT時要求實數/虛數分量,在機械應用(如振動測量)中它們更常用,幅度/相位格式在電氣測量中也常見到。圖4顯示了一個方波的功率譜幅值/相位和實數/虛數分量的例子。
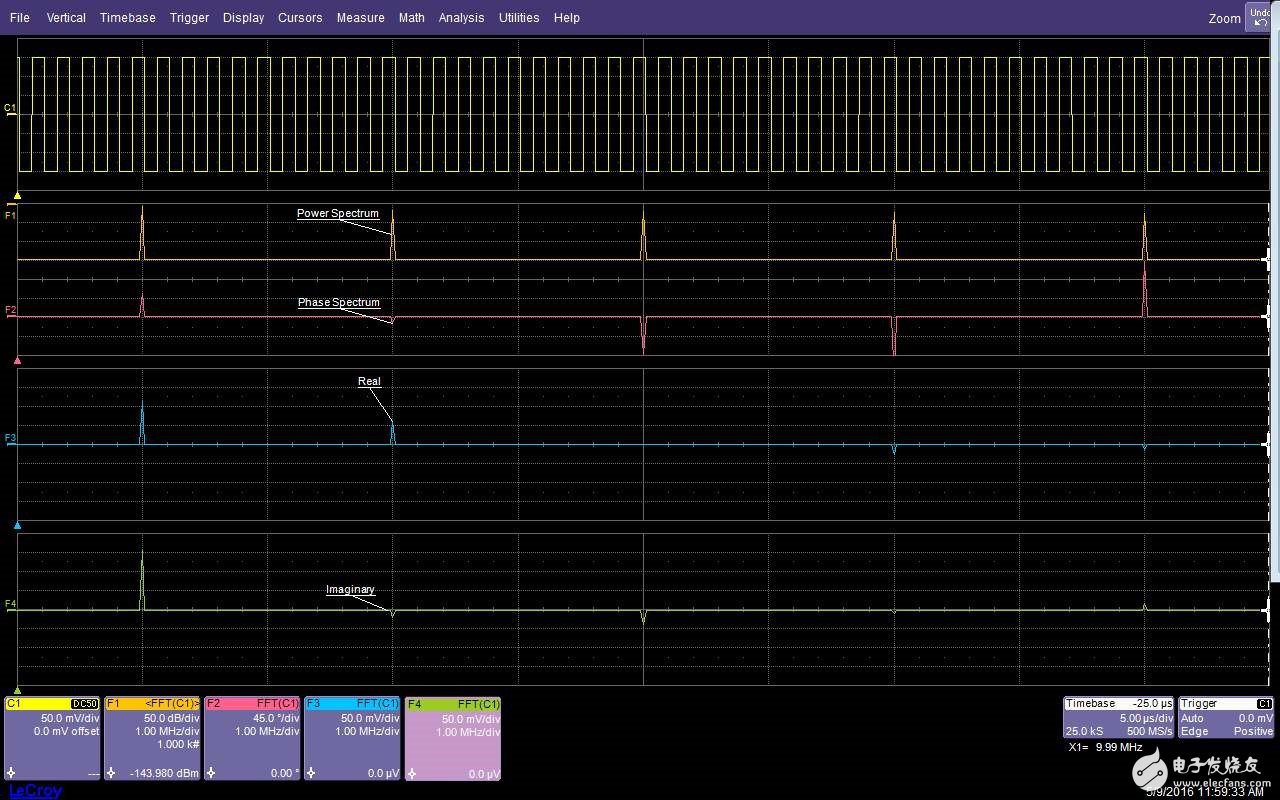
圖4:一個方波的FFT的功率譜幅值、相位、實數和虛數分量
相位譜使用垂直單位度,實數和虛數格式使用與源通道相同的垂直單位,在本例中是mV。對于類似這種方波的周期性波形,相位、實數和虛數格式只在基頻和諧波頻率點有有效值。
加權函數
示波器中實現的FFT具有有限的記錄長度,這將在頻譜顯示中引起問題,原因是獲取的波形的起點和終點的連續性問題。圖5顯示了起點和終點是如何影響頻譜形狀的。
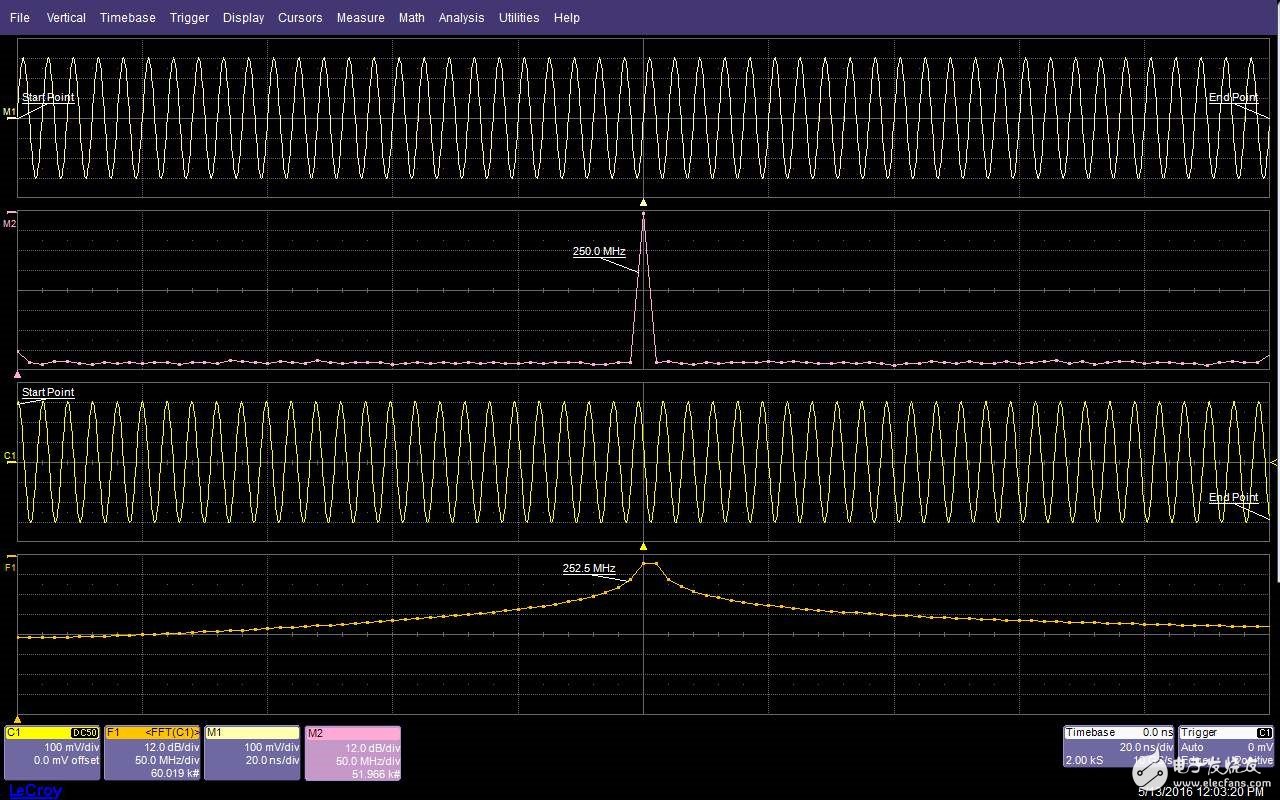
圖5:起點和終點的邊界條件將影響信號經FFT處理之后的頻譜形狀
圖5的上面兩個波形中,所采集的信號頻率是采樣率的因數,獲取的波形中存在整數的周期性,起點和終點處于相同的幅度,結果生成的頻譜非常窄。在下面兩個波形中,所采集的信號的頻率不是采樣速率的因數,起點和終點位于不同的電平。
這將導致時間記錄的不連續性。生成的頻譜變得更寬,峰值電平更低,原因是頻譜擴展(也稱為泄漏),即采集信號的能量被擴展到了相鄰頻率單元。更低的、與頻率有關的峰值響應被稱為“尖樁籬柵”效率或扇形損耗。加權(開窗)有助于最大限度地減小這些效應。
加權是將獲取的波形乘以一個窗口函數,通過調制將端點變為零。窗口函數的形狀決定了頻譜響應,包括頻譜線的形狀和任何邊帶的幅度。常用加權函數的特征如表1所示。
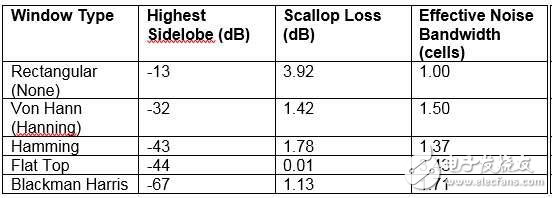
表1 常見FFT加權(窗口)函數的特征
這張表對每個窗口最大限度減小旁瓣和扇形損耗的能力進行了總結。圖6顯示了在相同輸入信號條件下窗口函數對譜線的影響。
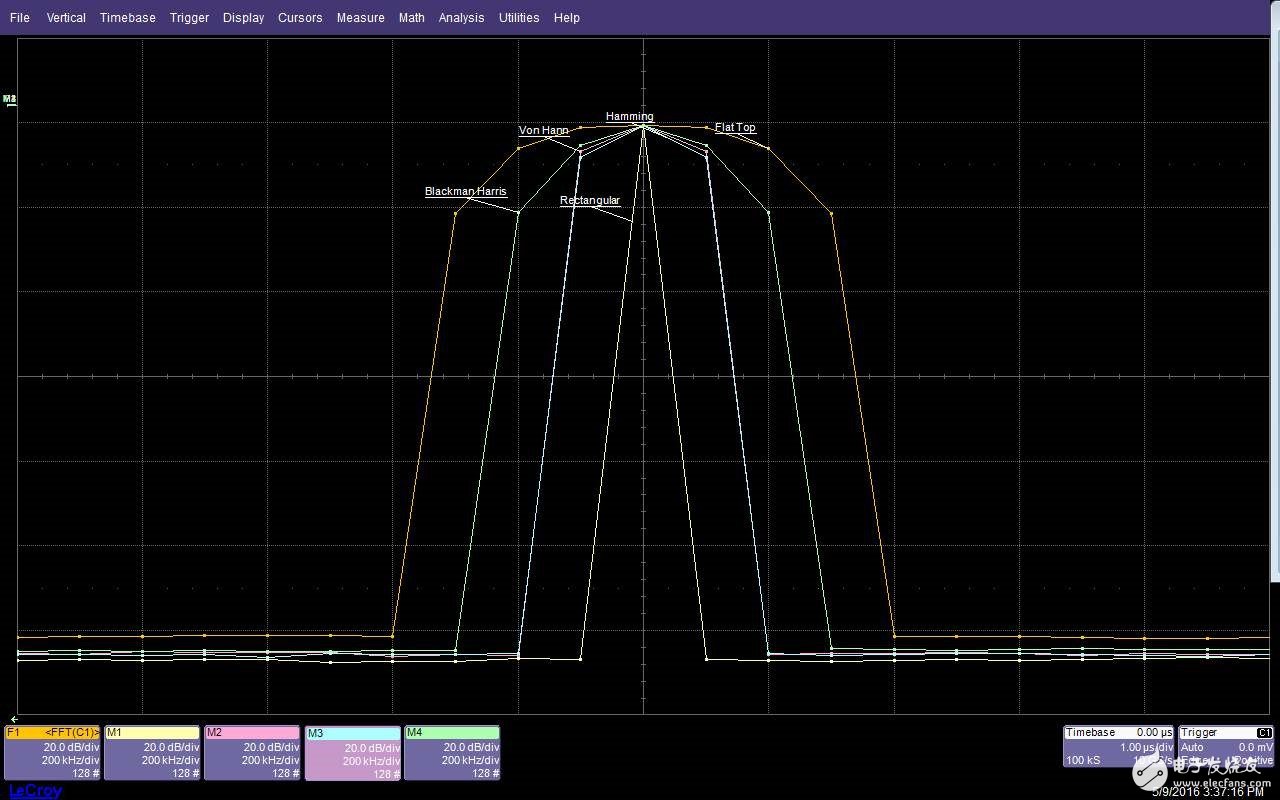
圖6:這個屏幕圖像比較了在相同輸入信號條件下不同加權函數對頻譜響應的影響
譜線變寬可以減小扇形損耗,這是有意義的,因為相鄰單元中的信號會在更高幅度點重合,以獲得更寬的響應,并最大限度地減小扇形損耗。
窗口函數的選擇取決于具體需求。如果你要測量比采集窗口小的瞬變,那么不要使用窗口函數,因為頻譜峰值的幅度將根據采集窗口中的瞬態位置發生改變。在這種情況下,矩形窗口(無加權)是最好的選擇。越窄的窗口響應可以提供越好的頻率分辨率和更寬的響應——Blackman Harris或平頂窗口——產生更為精確的幅度測量結果。如果你要兩者兼顧,一個好的折衷方案是Von Hann或Hamming窗口。
頻域平均
平均操作可以用來改善采集信號的信噪比,并且通常要求多次采集。平均可以在時域完成,也可以在頻域完成。與觸發事件不同步的信號,比如噪聲,將與平均次數呈正比衰減。圖7是頻域平均的一個例子。
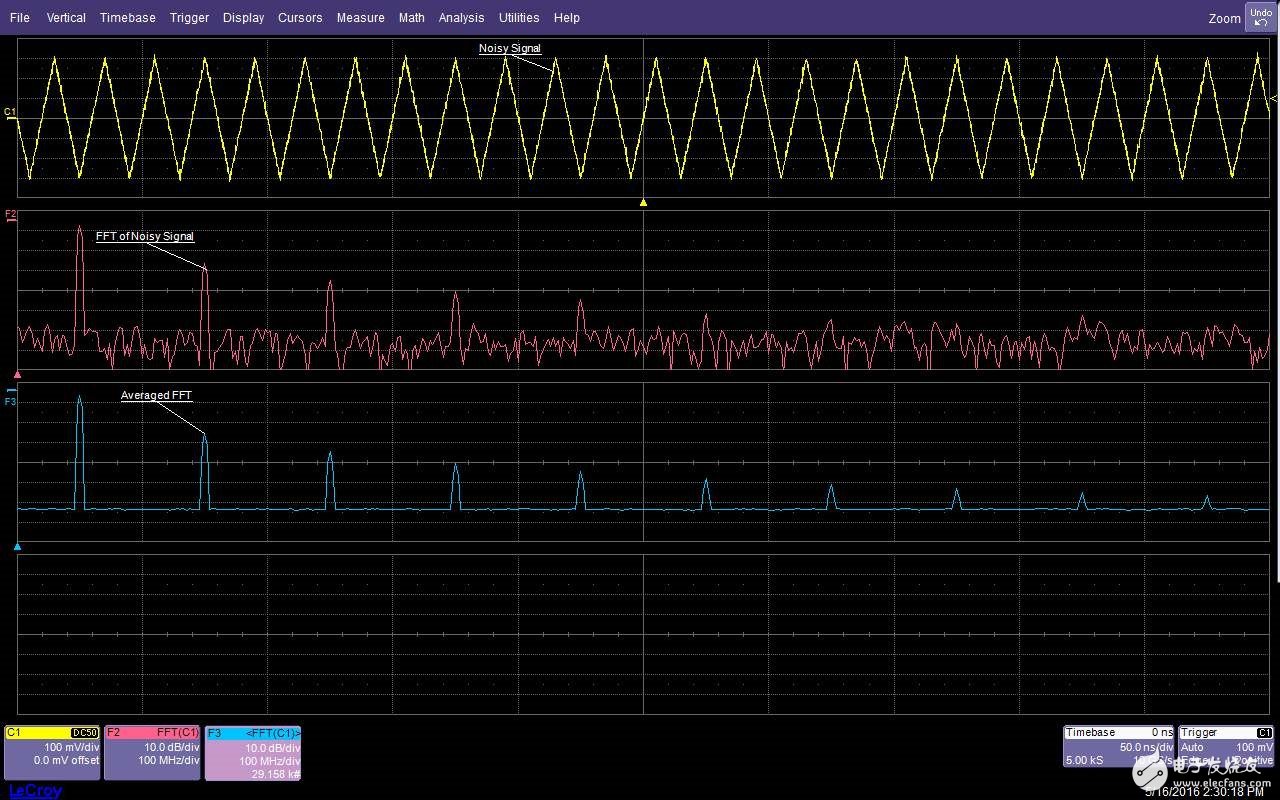
圖7:頻域平均可以改善信噪比,并提供更大的動態測量范圍。有噪信號FFT在經過許多次采集的平均后可以消除噪聲,從而看到更低電平的諧波
頻域中的平均是將多次采集的每個頻率單元的內容累加起來然后除以采集次數實現的。那些與采集不同步的信號將被平均為零,而同步信號則連續累加。在圖7中,有噪信號的FFT包含頻譜被擴展的噪聲分量,這些噪聲隱藏了低電平的諧波。平均有助于提高信噪比,減少噪聲,使得諧波分量可見。以同樣的方式,那些與采集不同步的信號幅度也將降低。
設置實例
考慮需要在一個4GHz帶寬的示波器上設置FFT,其頻帶寬度是10MHz,中心頻率是2.48GHz,分辨率帶寬為10kHz,用于分析一個連續的周期性信號。根據上述討論,只需簡單地設置示波器的時間/格參數就能完成分辨率帶寬的設置。10kHz的分辨率帶寬要求采集或捕獲時間為100μs,或者時間/格參數設為10μs /格。還應設置示波器的垂直靈敏度(電壓/格),以便信號占據至少90%的輸入范圍,盡量提高其動態范圍。
FFT的頻帶寬度由采樣率控制。由于這個寬度必須包含2.48GHz信號頻率,因此必須大于這個頻率的兩倍。5GHz或更高的頻率應該沒問題。示波器的最大采樣率是20 GS/s。利用示波器的時基設置來調整采集內存長度,可以獲得想要的采樣率。在本例使用的示波器中,將內存長度設為1MS,可以實現10GS/s的采樣率和100μs的采集時間。詳細的FFT設置見圖8。
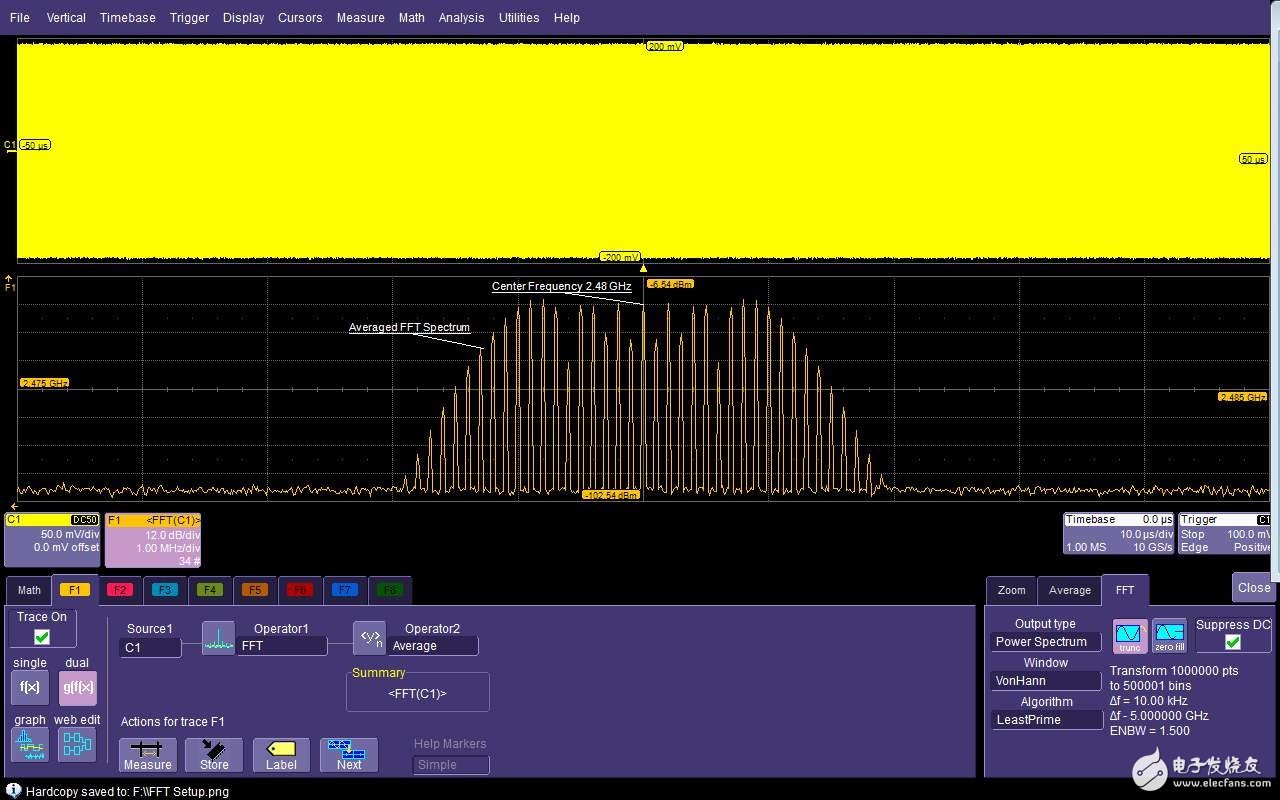
圖8:適合本例使用的主要FFT參數設置
數學函數F1的FFT欄包含一些主要的FFT設置,并被設置為顯示功率譜。由于信號被顯示為連續的,因此加權函數類型可以選擇Von Hann窗口,它可以在頻率分辨率和幅度平坦度之間提供很好的折衷。
FFT欄顯示分辨率帶寬(Δf)為10kHz,寬度為5GHz。縮放欄可以讓你將中心頻率設為2.48GHz,水平刻度設為1MHz/格,如圖8中的F1軌跡所示。
小結
本文討論了一些重要的FFT特性,解釋了如何利用這些特性設置FFT以實現高效的分析。等下次你要在示波器中使用FFT時希望能助你一臂之力。
 電子發燒友App
電子發燒友App















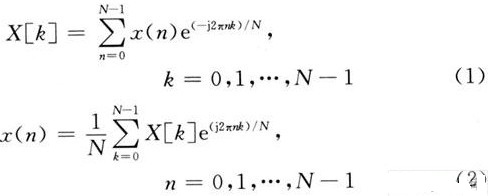
















評論