逐點比較法是我國數控機床中廣泛采用的一種插補方法,它能實現直線、圓弧和非圓二次曲線的插補,插補精度較高。
逐點比較法,顧名思義,就是每走一步都要將加工點的瞬時坐標同規定的圖形軌跡相比較,判斷其偏差,然后決定下一步的走向,如果加工點走到圖形外面去了,那么下一步就要向圖形里面走;如果加工點在圖形里面,那么下一步就要向圖形外面走,以縮小偏差。這樣就能得出一個非常接近規定圖形的軌跡,最大偏差不超過一個脈沖當量。
在逐點比較法中,每進給一步都須要進行偏差判別、坐標進給、新偏差計算和終點比較四個節拍。下面分別介紹逐點比較法直線插補和圓弧插補的原理。
一、 逐點比較法直線插補
如上所述,偏差計算是逐點比較法關鍵的一步。下面以第Ⅰ象限直線為例導出其偏差計算公式。 
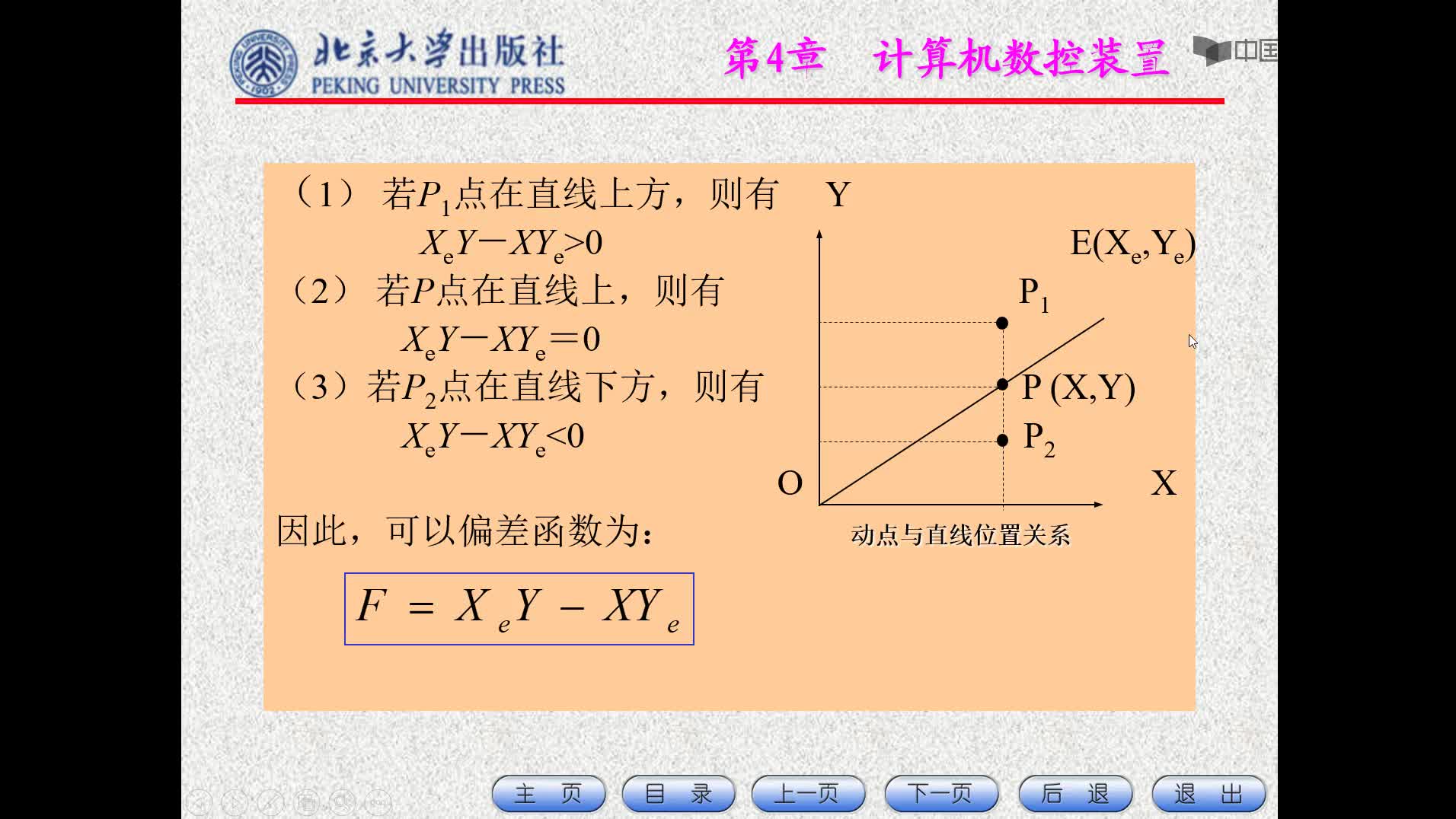
如圖2—1所示,假定直線 的起點為坐標原點,終點A的坐標為 為加工點,若P點正好處在直線 上,那么下式成立:
? 若任意點 在直線 的上方(嚴格地說,在直線 與y軸所成夾角區域內),那么有下述關系成立:
亦即:????????????????????????? 由此可以取偏差判別函數 為:
由 的數值(稱為“偏差”)就可以判別出P點與直線的相對位置。即:
當 =0時,點 正好落在直線上;
當 >0時,點 落在直線的上方;
當 <0時,點 落在直線的下方。
從圖2—1看出,對于起點在原點,終點為A( )的第Ⅰ象限直線OA來說,當點P在直線上方(即 >0)時,應該向+x方向發一個脈沖,使機床刀具向+x方向前進一步,以接近該直線;當點P在直線下方(即 <0)時,應該向+y方向發一個脈沖,使機床刀具向+y方向前進一步,趨向該直線;當點P正好在直線上(即 =0)時,既可向+x方向發一脈沖,也可向+y方向發一脈沖。因此通常將 >0和 =0歸于一類,即 ≥0。這樣從坐標原點開始,走一步,算一次,判別 ,再趨向直線,逐點接近直線 ,步步前進。當兩個方向所走的步數和終點坐標A( )值相等時,發出終點到達信號,停止插補。
對于圖2—1的加工直線OA,我們運用上述法則,根據偏差判別函數值,就可以獲得如圖中折線段那樣的近似直線。
但是按照上述法則進行 的運算時,要作乘法和減法運算,這對于計算過程以及具體電路實現起來都不很方便。對于計算機而言,這樣會影響速度;對于專用控制機而言,會增加硬件設備。因此應簡化運算,通常采用的是迭代法,或稱遞推法,即每走一步后新加工點的加工偏差值用前一點的加工偏差遞推出來。下面推導該遞推式:
已經知道,加工點的坐標為( )時的偏差為:
若 ≥0時,則向x軸發出一進給脈沖,刀具從這點即( )點向x方向前進一步,到達新加工點P( ), ,因此新加工點P( )的偏差值為
即:??????????????????????????????????????????????????????????????????????????????????????????????? (2-1)
如果某一時刻,加工點P( )的 <0,則向y軸發出一個進給脈沖,刀具從這一點向y方向前進一步,新加工點P( )的偏差值為
? 即:??
????????????????????????????????????????????????????? (2-2)
? 根據式(2—1)及式(2—2)可以看出,新加工點的偏差完全可以用前一加工點的偏差遞推出來。
綜上所述,逐點比較法的直線插補過程為每走一步要進行以下4個節拍(步驟),即判別、進給、運算、比較。
(1) 判別。根據偏差值確定刀具位置是在直線的上方(或線上),還是在直線的下方。
(2) 進給。根據判別的結果,決定控制哪個坐標(x或y)移動一步。
(3) 運算。計算出刀具移動后的新偏差,提供給下一步作判別依據。根據式(2—1)及式(2—2)來計算新加工點的偏差,使運算大大簡化。但是每一新加工點的偏差是由前一點偏差 推算出來的,并且一直遞推下去,這樣就要知道開始加工時那一點的偏差是多少。當開始加工時,我們是以人工方式將刀具移到加工起點,即所謂“對刀”,這一點當然沒有偏差,所以開始加工點的 =0。
(4) 比較。在計算偏差的同時,還要進行一次終點比較,以確定是否到達了終點。若已經到達,就不再進行運算,并發出停機或轉換新程序段的信號。
下面以實例來驗證圖2—1。設欲加工直線OA,其終點坐標為 =5*, =3*,則終點判別值可取為 (終點判別方法詳見下述)。開始時偏差 ,加工過程的運算節拍如表2—1所示。
圖2-2? 逐點比較法直線插補過程
表2-1?? 逐點比較法直線插補運算舉例
|
序號 |
???????????????????????????????????????????????? 工????????? 作????????? 節?????????? 拍 | |||
|
第1拍:判別 |
第2拍:進給 |
第3拍:運算 |
第4拍:比較 | |
|
1 |
F00=0 |
+?x |
F10= F00-ye=0-3= -3 |
E7= E8-1=7 |
|
2 |
F10(= -3)<0 |
+?y |
F11 = F10+xe= -3+5=2
|
E6= E7-1=6 |
|
3 |
F11(= 2)>0 |
+?x |
F21= F11-ye=2-3= -1 |
E5= E6-1=5 |
|
4 |
F21(= -1) <0 |
+?y |
F22= F21+xe= -1+5=4 |
E4= E5-1=4 |
|
5 |
F22(= 4)>0 |
+?x |
F32= F22-ye=4-3= 1 |
E3= E4-1=3 |
|
6 |
F32(= 1)>0 |
+?x |
F42 = F32-ye=1-3= -2 |
E2= E3-1=2 |
|
7 |
F42(= -2)<0 |
+?y |
F43= F42+xe= -2+5=3 |
E1=E2-1=1 |
|
8 |
F43(= 3)>0 |
+?x |
F53= F43-ye=3-3=0 |
E0=E1-1=0 |
|
|
|
|
|
到達終點 |
二、 逐點比較法圓弧插補
加工一個圓弧,很容易聯想到把加工點到圓心的距離和該圓的名義半徑相比較來反映加工偏差。這里,我們以第Ⅰ象限逆圓弧為例導出其偏差計算公式。設要加工圖2—3所示第Ⅰ象限逆時針走向的圓弧,半徑為R,以原點為圓心,起點坐標為A( ),對于圓弧上任一加工點的坐標設為P( ),P點與圓心的距離 的平方為 ,現在討論這一加工點的加工偏差。
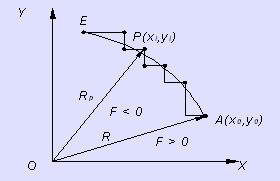
圖2-3? 圓弧插補過程
點擊進入動畫觀看逐點比較法圓弧插補???????????????????????????????????????????????????
若點P( )正好落在圓弧上,則下式成立:
若加工點P( )在圓弧外側,則 >R,即:
若加工點P( )在圓弧內側,則
將上面各式分別改寫為下列形式:
(加工點在圓弧上)
(加工點在圓弧外側)
?(加工點在圓弧內側)
取加工偏差判別式為:????????
運用上述法則,利用偏差判別式,即獲得圖2—2折線所示的近似圓弧。
若P( )在圓弧外或圓弧上,即滿足 ≥0的條件時,應向x軸發出一個負向運動的進給脈沖(—Δx),即向圓內走一步。若P( )在圓弧內側,即滿足 <0的條件,則向y軸發出一個正向運動的進給脈沖(+Δy),即向圓弧外走一步。為了簡化偏差判別式的運算,仍用遞推法來推算下一步新的加工偏差。
設加工點P( )在圓弧外側或圓弧上,則加工偏差為
x坐標需向負方向進給一步(—Δx),移到新的加工點P( )位置,此時新加工點的x坐標值為 ,y坐標值仍為 ,新加工點P( )的加工偏差為:
經展開并整理,得:??? (2-3)
設加工點P( )在圓弧的內側,則:<0
那么,y坐標需向正方向進給一步(+Δy),移到新加工點P( ),此時新加工點的x坐標值仍為 ,y坐標值則改為 ,新加工點P( )的加工偏差為:
,展開上式,并整理得:
綜上所述可知:當 ≥0時,應走—Δx,新偏差為 ,動點(加工點)坐標為 , ;當 <0時,應走+Δy,新偏差為 ,動點坐標為 , 。
下面舉例說明插補過程。設欲加工第Ⅰ象限逆時針走向的圓弧(見圖2—4),起點A的坐標是 ,終點E的坐標是 ,終點判別值:

圖2-4? 圓弧實際軌跡

???? 圖2-5? 逐點比較法圓弧插補過程
加工過程的運算節拍見表2—3,插補后獲得的實際軌跡如圖2—3折線所示。
可見,圓弧插補偏差計算的遞推公式也是比較簡單的。但計算偏差的同時,還要對動點的坐標進行加1、減1運算,為下一點的偏差計算做好準備。
和直線插補一樣,除偏差計算外,還要進行終點判別計算。每走一步,都要從兩坐標方向總步數中減去1,直至總步數被減為零(發終點到達信號)時為止,才終止計算。?????????????????????????????????????????
??????? 表2-3? 逐點比較法圓弧插補運算舉例?
|
序號 |
工作節拍
| |||
|
第1拍:判別 |
第2拍:進給 |
第3拍:運算 |
第4拍:比較 | |
|
1 |
?? F=0 |
-△x |
????????? F=0-2*4+1=7 |
E=6-1=5(≠0) |
|
2 |
? F(=-7)<0 |
+△y |
????????? F=-7+2*3+1=0 ????????? x=3,y=3+1=4 |
E=5-1=4(≠0) |
|
3 |
? F=0 |
-△x |
???????? F=0-2*3+1=-5 ???????? x=3-1=2,y=4 |
E=4-1=3(≠0) |
|
4 |
?F(=-5)<0 |
+△y |
??????? F=-5+2*4+1=4 ??????? x=2,y=4+1=5 |
E=3-1=2(≠0) |
|
5 |
?F(=4)>0 |
-△x |
??????? F=4-2*2+1=1 ????? ? x=2-1=1,y=5 |
E=2-1=1≠0) |
|
6 |
?F(=1)>0 |
-△x |
????? ? F=1-2*1+1=0 ????? ? x=1-1=0,y=5 |
E=1-1=0(終止) |
?逐點比較法插補第Ⅰ象限直線和第Ⅰ象限逆圓弧的計算流程圖分別見圖2—4和圖2—5。
??????????? 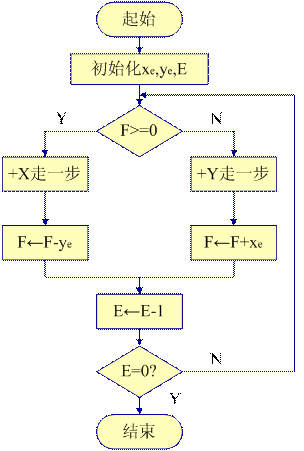
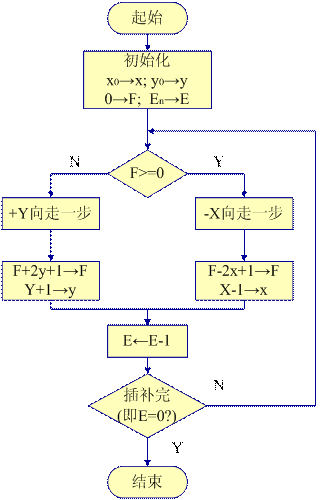
? 圖2-4? 直線插補計算流程圖? 圖2-5?? 圓弧插補計算流程圖
?
 電子發燒友App
電子發燒友App






































評論