2.1.1 空間點陣和晶胞
?具有代表性的基本單元(最小平行六面體)作為點陣的組成單元,稱為晶胞。將晶胞作三維的重復堆砌就構成了空間點陣。
為了便于分析研究晶體中質點的排列規律性,可先將實際晶體結構看成完整無缺的理想晶體并簡化,將其中每個質點抽象為規則排列于空間的幾何點,稱之為陣點。這些陣點在空間呈周期性規則排列并具有完全相同的周圍環境,這種由它們在三維空間規則排列的陣列稱為空間點陣,簡稱點陣。同一空間點陣可因選取方式不同而得到不相同的晶胞?
晶胞、晶軸和點陣矢量
根據6個點陣參數間的相互關系,可將全部空間點陣歸屬于7種類型,即7個晶系。按照"每個陣點的周圍環境相同"的要求,布拉菲(Bravais A.)用數學方法推導出能夠反映空間點陣全部特征的單位平面六面體只有14種,這14種空間點陣也稱布拉菲點陣。
|
布拉非點陣 |
晶系 |
布拉非點陣 |
晶系 |
|
簡單三斜 |
三斜 |
簡單六方 |
六方 |
|
簡單單斜 |
單斜 |
簡單菱方 |
菱方 |
|
簡單正交 |
正交 |
簡單四方 |
四方 |
|
簡單立方 |
立方 |
2.1.2 晶向指數和晶面指數
為了便于確定和區別晶體中不同方位的晶向和晶面,國際上通用密勒(Miller)指數來統一標定晶
向指數與晶面指數。
1.晶向指數 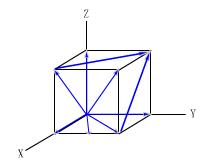
圖2.6?正交晶系一些重要晶向的晶向指數
晶向指數的確定步驟如下:
1)以晶胞的某一陣點O為原點,過原點O的晶軸為坐標軸x,y, z, 以晶胞點陣矢量的長度作為坐標軸的長度單位。
2)過原點O作一直線OP,使其平行于待定晶向。
3)在直線OP上選取距原點O最近的一個陣點P,確定P點的3個坐標值。
4)將這3個坐標值化為最小整數u,v,w,加以方括號,[u v w]即為待定晶向的晶向指數。
2.晶面指數
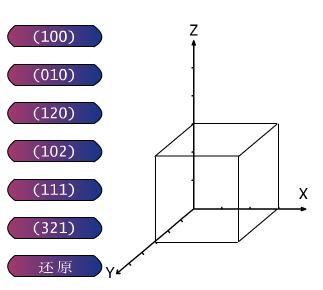
圖2.7?正交點陣中一些晶面的面指數
?晶面指數標定步驟如下:
1)在點陣中設定參考坐標系,設置方法與確定晶向指數時相同;
2)求得待定晶面在三個晶軸上的截距,若該晶面與某軸平行,則在此軸上截距為無窮大;若該晶面與某軸負方向相截,則在此軸上截距為一負值;
3)取各截距的倒數;
4)將三倒數化為互質的整數比,并加上圓括號,即表示該晶面的指數,記為( h k l )。
?晶面指數所代表的不僅是某一晶面,而是代表著一組相互平行的晶面。另外,在晶體內凡晶面間距和晶面上原子的分布完全相同,只是空間位向不同的晶面可以歸并為同一晶面族,以{h k l}表示,它代表由對稱性相聯系的若干組等效晶面的總和。?
?
3.六方晶系指數
?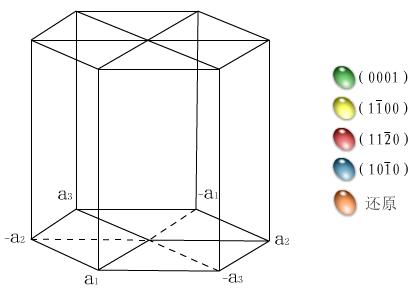
圖2.8 六方晶系一些晶面的指數
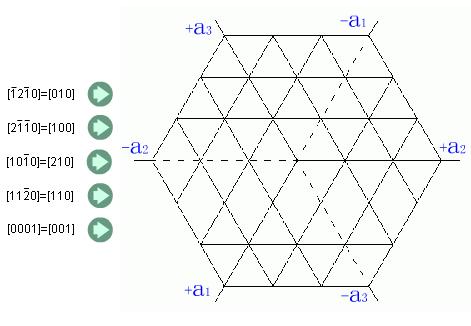
圖2.9 六方晶系晶像指數的表示方法(c軸與圖面垂直)
六方晶系的晶向指數和晶面指數同樣可以應用上述方法標定,這時取a1,a2,c為晶軸,而a1軸與a2軸的夾角為120度,c軸與a1,a2軸相垂直,如圖2.13所示。但這種方法標定的晶面指數和晶向指數,不能完全顯示六方晶系的對稱性,為了更好地表達其對稱性,根據六方晶系的對稱特點,對六方晶系采用a1,a2,a3及c四個晶軸,a1,a2,a3之間的夾角均為120度,這樣,其晶面指數就以(h k i l)四個指數來表示。
根據幾何學可知,三維空間獨立的坐標軸最多不超過三個。前三個指數中只有兩個是獨立的,它們之間存在以下關系:i =- ( h + k ) 。
采用4軸坐標時,晶向指數的確定原則仍同前述(見圖2.14),晶向指數可用{u v t w}來表示,這里 u + v = - t。
?
4.晶帶
?所有平行或相交于同一直線的這些晶面構成一個晶軸,此直線稱為晶帶軸。屬此晶帶的晶面稱為晶帶面。
?晶帶軸[u v w]與該晶帶的晶面(h k l)之間存在以下關系: hu + kv + lw = 0
?凡滿足此關系的晶面都屬于以[u v w]為晶帶軸的晶帶,故此關系式也稱作晶帶定律。
5.晶面間距
圖2.10 晶面間距
圖2.11 晶面間距公式的推導
?由晶面指數還可求出面間距dhkl。通常,低指數的面間距較大,而高指數的晶面間距則較小。
2.1.3 晶體的對稱性
1.對稱元素
?晶體的對稱元素可分為宏觀和微觀兩類。宏觀對稱元素反映出晶體外形和其宏觀性質的
?對稱性。而微觀對稱元素與宏觀對稱元素配合運用就能反映出晶體中原子排列的對稱性。
?a.宏觀對稱元素;
1)回轉對稱軸:當晶體繞某一軸回轉而能完全復原時,此軸即為回轉對稱軸。注意該軸線定要通過晶格單元的幾何中心,且位于該幾何中心與角頂或棱邊的中心或面心的連線上。在回轉一周的過程中,晶體能復原n次,就稱為n次對稱軸。
2)對稱面:晶體通過某一平面作鏡像反映而能復原,則該平面稱為對稱面或鏡面。
3)對稱中心:晶體通過某一平面作鏡像反映而能復原,則該平面稱為對稱面或鏡面。
4)回轉-反演軸:若晶體繞某一軸回轉一定角度(360/n),再以軸上的一個中心點作反演之后能得到復原時,此軸稱為回轉-反演軸。
圖2.12 對稱軸
圖2.13 對稱面
圖2.14 對稱中心
圖2.15 回轉-反演軸
?b.微觀對稱元素;
??(1)滑動面。
??? 一個對稱面加上沿著此面的平移所組成,晶體結構可借此面的反映并沿此面平移
??? 一段距離而復原。
??(2)螺旋軸。
??? 回轉軸和平行于軸的平移所構成。
2.32種點群
?點群是指一個晶體中所有點對稱元素的集合。點群在宏觀上表現為晶體外形的對稱。利
?用組合定理可導出晶體外形中只能有32種對稱點群。
2.1.4 極射投影
1.極射投影原理
極射投影的原理如圖2.23所示。先在參考球中選定一條過球心的直線AB(直線),過A點作一平面與參考球相切,該平面即為投影面,也稱極射面。若球面上有一極點P,連接BP并延長之,使其與投影面相交于P',P'即為極點P在投影面上的極射投影。過球心作一平面N'E'S'W'與AB垂直(與投影面平行),它在球面上形成一個直徑與球徑相等的圓稱大圓。大圓在投影面上的投影為N'E'S'W'也是一個圓,稱為基圓。所有位于左半球球面上的極點,投影后的極射投影點均將落在基圓之內。然后將投影面移至B點,并以A點為投影點,將所有位于右半球球面上的極點投射到位于B處的投影面上,并冠以負號。最后將A處和B處的極射投影圖重疊地畫在一張圖上。這樣,球面上所有可能出現的極點,都可以包括在同一張極射投影圖上。
2.吳氏(WulFF)網
圖2.16 吳氏網(分度為2°)
3.標準投影
圖2.17 立方晶體詳細的(001)標準投影圖
以晶體的某個晶面平行于投影面上作出全部主要晶面的極射投影圖稱為標準投影。一般選擇一些重要的低指數的晶面作為投影面,這樣得到的圖形能反映晶體的對稱性。立方晶系常用的投影面是( 001 ),( 110 ) 和( 111 );六方晶系則為( 0001 )。立方晶系的( 001 )標準投影如上圖所示。
 電子發燒友App
電子發燒友App


























評論