1.電機工作的物理原理 ? ? ?

1.1麥克斯韋方程組

電機(elektrische Maschine)是一個對電磁能和機械能進行不斷轉換的換能器，當輸入電能，電機就可以源源不斷地輸出轉矩和機械能，即電動機；反之，如果外力不斷推動電機軸，輸入機械能，電機就能反向從導線端源源不斷輸出電壓和電能，也即發電機。歷史上曾經把靜態不動的變壓器也算作電機，但是后來逐漸演化成專指電動機(Motor)和發電機(Generator)。電機的一個優點是它們的損耗相對較小，因此它們實現了高效率。大型電機可以實現高達99％的效率。

談及電磁系統，就繞不開麥克斯韋方程組，在宏觀世界乃至微觀世界都可以很有效地使用用麥克斯韋方程組來描述系統性質。麥克斯韋方程組經過對前人對電磁現象研究地總結，有四條非常基本的方程，有微分形式和積分形式。現在來考察積分形式地麥克斯韋方程組：

(1.1)?

(1.2)?

上面兩式描述了場密度的通量，分別在一個封閉空間曲面內流出電位移??的總和和磁感應??的總和,根據高中所學知識，電場可由點電荷激發產生，磁場不能由磁單極子激發，而是延著路徑封閉，所以電場是有源的，磁場是無源的。所以總的電位移通量為總電荷量q，總磁通量為0。

(1.3)?

(1.4)?

上述兩式描述了場強度的旋量，分別在一個封閉空間曲線上沿著曲線路徑走一圈的總電場強度和總磁場強度的積分，對應了激發出來的磁通變化率和電位移變化率（電流強度）。通過高斯公式和斯托克斯公式還可以將上述四個式子改寫為微分形式：

(1.5)?

(1.6)?

(1.7)?

(1.8)?

?為Nabla算子，與向量點乘計算散度，叉乘計算旋度，??為電荷體密度，??為電流密度。上述幾條式子基本可以描述所有一切電機系統中會發生的電磁行為。

1.2材料的極化和磁化

在一個外加電場中，物質分子會因為極性受場強影響而發生取向變化，原有排布不均勻的各種大小分子團形成的電疇會因為外加場，電荷分布取向趨同而發生極化。

(1.9)?

?為真空電容率，亦真空介電常數，??為相對介電常數，由材料本身性質決定。（1.9）描述了外加電場和對應極化強度??共同構成的電位移密度。

在一個外加磁場里，同理可以得到對應的磁疇和磁化強度??與電場不同的是引入了一個磁極化強度??，它描述了材料和真空環境下磁感應強度的差值。

(1.10)?

?為真空磁導率，??為相對磁導率，描述了材料允許磁場通過的能力。如果，則為抗磁性，材料阻礙磁場通過；如果??，則表現為順磁性，材料順應磁場通過；??為鐵磁性，材料比如鐵鈷鎳會在磁化以后增強磁場且再移走磁場后保留一定強度磁場，即所謂剩磁。在電機運行的過程中會不斷出現磁化和退磁，所以也應該注意對不同材料磁滯回線的考察。

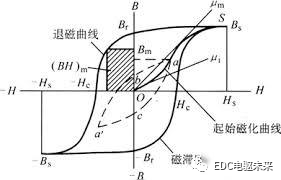
圖1.1 磁滯回線

磁滯回線描述了外加磁場強??作用下一種磁性材料隨著場強增大而不斷增強其磁感應強度，該磁感應強度在達到磁飽和以后很難跟隨場強繼續增強，當外部磁場強慢慢減小至零，可以看到退磁曲線過零點時，依然保有剩磁??，這個剩磁就明示了一般永磁體的制造原理，即定向磁化再逐步退磁。而當施加反向磁場致使磁感應強度歸零乃至反向增大，這個過零點稱為矯頑強度?

1.3電磁力

電機最大的價值就是實現電能到機械能的轉化，對外做功，執行目標運動。帶電粒子在磁場中運動受到垂直于運動方向的洛倫茲力，其宏觀表現就是安培力??，可以使用左手定則判斷方向，??為電流方向下導體在磁場中有效長度。

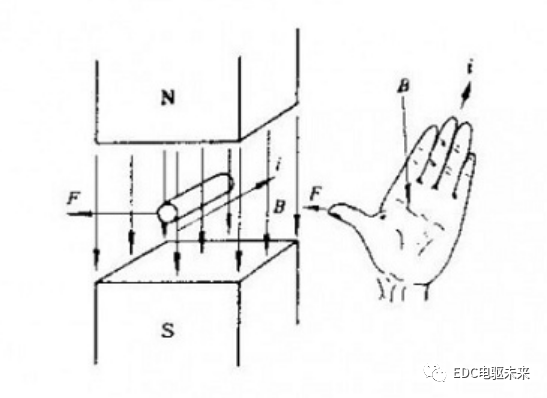
圖1.2 用以判斷電流，磁感應強度和受力方向的左手定則

靜電場里也有對應的電場力??。而磁場和電場本身都是場，對其中電荷或者電流元施加作用力時，依賴于體積和場密度，因而可以用場的觀點來考察對應的場力：

(1.11)?

(1.12)?

上述兩式依然保持了對稱性，電荷體密度?在一定體積內由于電場場強產生了電能力密度??，電流密度??也在一定體積內由于磁場場強產生了磁能力密度??（以上式(1.12)必須在材料各向同性和恒定電流情況下方可使用）這種表述方式啟發我們可以直接考察電磁場的能量和能量密度，這樣可以確定某一點的電磁勢能通過求梯度來獲得對應的電磁力密度從而求得對應考察物體受到的總的電磁力了。

1.4線圈模型

線圈是一個構成電機模型的基本元素，它橋接了電機的電路模型和實物的物理模型。一段直線通電導體會在周圍產生環形磁場(根據式1.4)，當導體首尾閉合后，環形磁場在導體環中心形成豎直通過導體環的磁力線，比如螺線管。

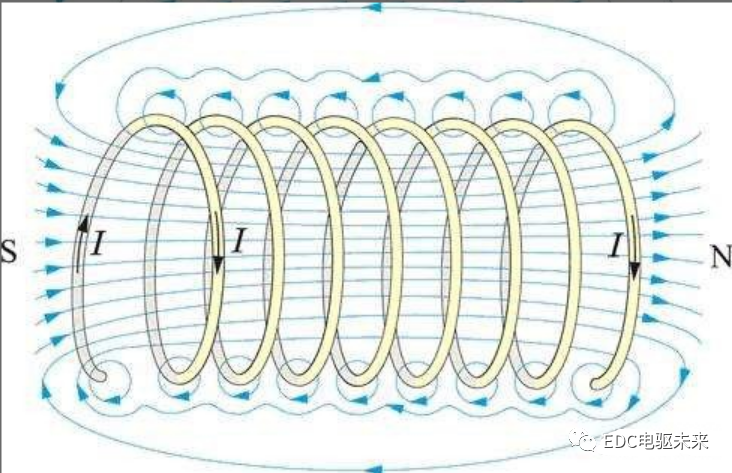
圖1.3 螺線管和對應磁力線分布情況

只考慮通電導體上的電流，(1.4)簡化為：

(1.13)?

?磁動勢(magnetische Durchfluchtung)，是激發磁場強度的源頭，本質為一段封閉導體上通過的總電流強度，單位為[A]。因為實際操作時會把通電導線纏繞成線圈，所以導線電流是離散化的，(1.13)改寫為：

(1.14)?

?為線圈總纏繞數，即匝數。可見如果匝數越多，總電流就越大，磁動勢就越大，能激發的磁場就越強。

電生磁，磁也能生電，一個處在時變磁場里的單匝線圈會在導線兩端感應出電壓，此現象可由(1.3)描述，當我們把線圈通過面積里的磁感應強度求和即可得到總的磁通量

(1.15)?

可知磁感應強度也可以理解為磁通密度，代入(1.3)可得

(1.16)?

?為感應電動勢，考慮磁通變化兩種形式，一是變化線圈面積而是變化磁通密度，則有

(1.17)?

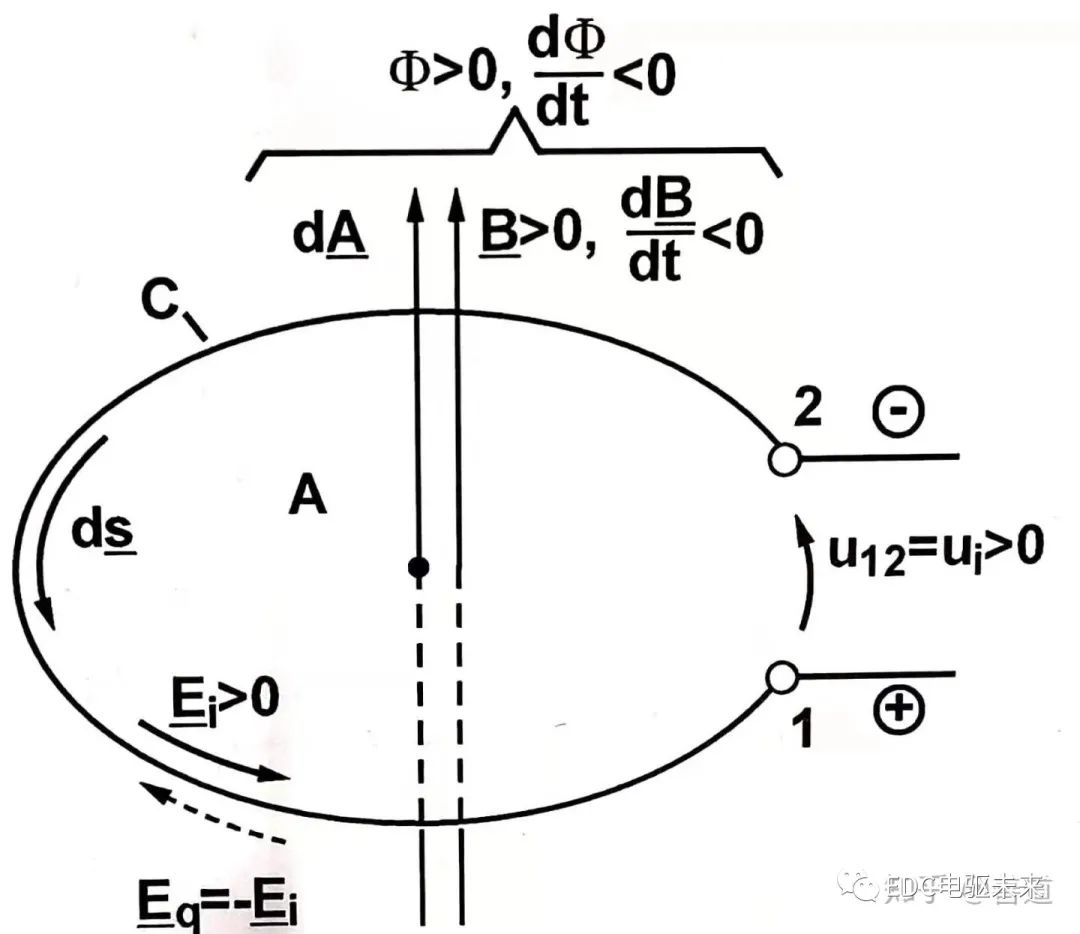
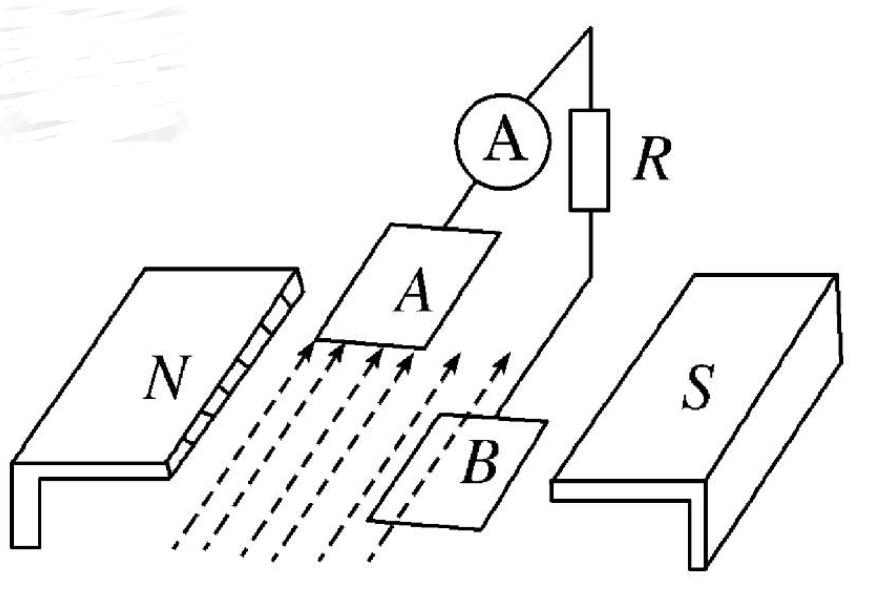
圖1.4.1形式變換的感應電動勢

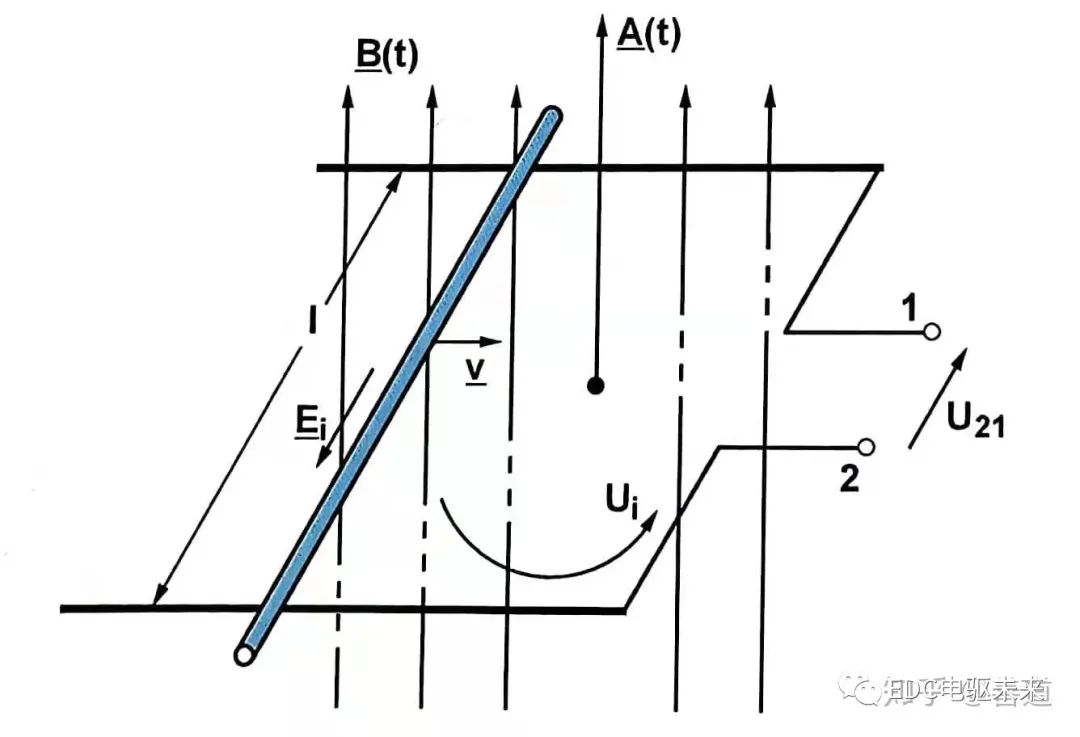
圖1.4.2平移變換的感應電動勢

前一部分是形式變換的感應電動勢(transformatisch induzierte Spannung)，后一部分是平移變換的感應電動勢(translatorisch induzierte Spannung)。前者磁通密度時變，后者有效線圈面積時變。這個感應原理在高中物理時會被提及，也就是所謂的楞次定理。

當一個線圈有好多匝數的時候，總的有效磁通正好是擴大了線圈匝整數倍，于是引入磁鏈的概念。定義磁鏈??。注意，磁鏈和磁通一樣都是標量。因為電流本身變化也能引起磁通變化，其趨勢為阻礙磁通變化，可以做出定義

(1.18)?

(1.19)?

?為變化的電流強度，?為自感系數，單位亨利[H]，其大小和線圈體積形狀，匝數，磁導率都有關系。電機中線圈都會為了提高磁導率而讓線圈中間加入鐵磁性材料，比如鐵芯，這樣線圈就會繞在鐵芯上，故而被稱為繞組(Wicklung)。

對于一段線性各相同性的材料來說，它的自感系數可由以下公式近似描述

(1.20)?

自感就是一個線圈自身電流變化感應出阻遏電壓的現象，其趨勢為阻礙電流變化，當兩個線圈靠近時，他們彼此除了自己的自感，還會因為鄰近的線圈上電流變化而產生互感

(1.21)?

線性各相同性的材料的互感系數??用上式近似表達，可見互感同時受到兩個線圈的匝數影響。

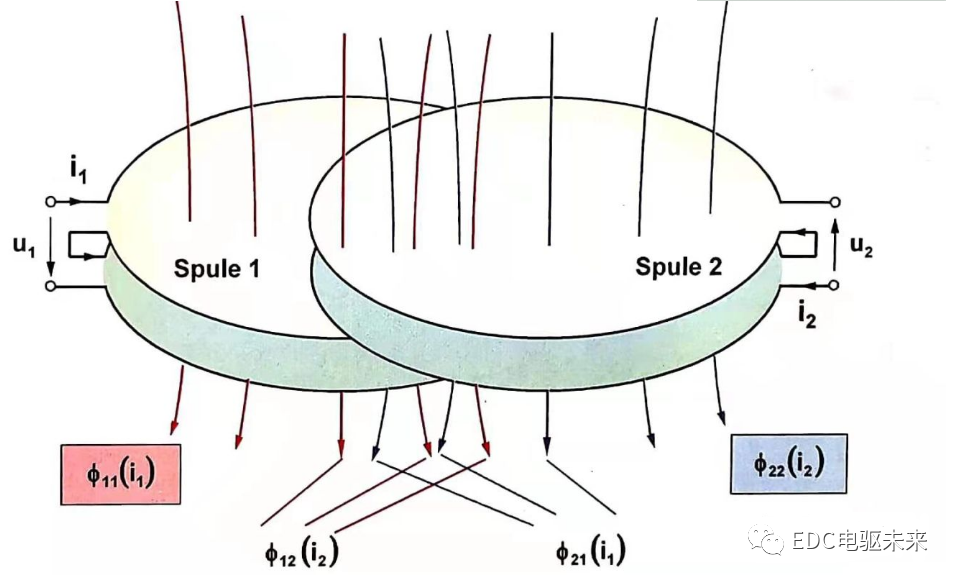
圖1.5 同時穿越線圈1(Spule 1)和線圈2(Spule 2)的磁場下的耦合感應

忽略電阻，考察兩段臨近線圈的自感和互感情況，由圖1.5可列出電壓方程

(1.22)?

(1.23)?

由于耦合部分擁有同樣的材料參數和形狀所以產生的互感系數是相等的??，于是在倆線圈上分別產生的耦合磁鏈大小正比于對應線圈上的電流強度

(1.24)?

1.5電路和磁路的歐姆定理

在中學的時候我們學習過歐姆定理，即一段導體的電阻為兩端電壓和電流之比，描述電阻材料本身也有公式，??為電導率，它正好為電阻率??的倒數，描述了對電流的導通能力。除了應用電阻，還可以使用電導??描述電壓電流之間的關系：

(1.25)?

(1.26)?

現在考察單位面積上的電流強度，即電流密度??（?為單位矢量），電流密度為矢量，方向指向電流方向。可以結合電壓公式??以及(1.25)改寫(1.26)為：

(1.27)?

上式描述了微觀時歐姆定理，即導體外加恒定場強下對應的電流密度的變化。

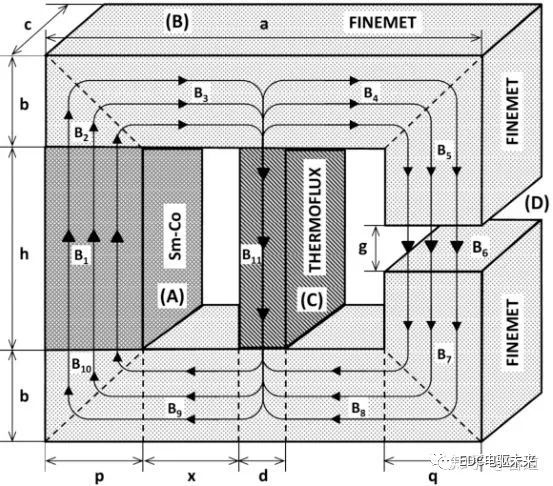
圖1.6 整塊鐵芯的磁通和磁路

在一個磁路中，磁通(magnetische Fluss)也是一種流量，不同材料對磁通的阻礙程度也各不相同，因而可以類比電路的歐姆定理引入磁阻??的概念(單位[A/Vs])，由磁動勢類比于電動勢，可以得到新的對應關系

(1.28)?

?為磁通量通過一段磁路的有效長度，??為對應的磁通面積。上式與電阻公式很像。讓我們再對磁阻公式變形，可以繼續得到

(1.29)?

可見在單位上磁阻其實和電感系數是倒數。

繼續類比電導的概念，可得磁導??(magnetische Leitwert,單位[H]或者[Ωs])

(1.30)?

(1.31)?

在電路中我們對(1.26)求微元，得到微觀的歐姆定理，那么對應到磁路的微觀歐姆定理是什么呢？我們可以繼續改寫式(1.31)，注意到磁通本身就有磁通密度??,那么可得

(1.32)?

所以微觀磁路歐姆定理就是式(1.10)，磁場強度下就是恒強磁場的磁化所得磁通密度。

對磁阻的計算分析可以用來實現對整個電機繞組極，鐵芯部分和中間氣隙部分的磁通的微元分析，可以實現對整個磁路進行離散的有限元分析FEM(Finite-Elemente-Methode)。在磁路里也完全可以應用電路的基爾霍夫定理進行分析，十分直觀方便。

1.6小結

到現在，一些電機所需的基本物理知識基本上都覆蓋到了。

有讀者建議我應該總結一個電磁對應關系的表格，這樣便于記憶和理解，于是在此次修訂中在小結里給出附表。

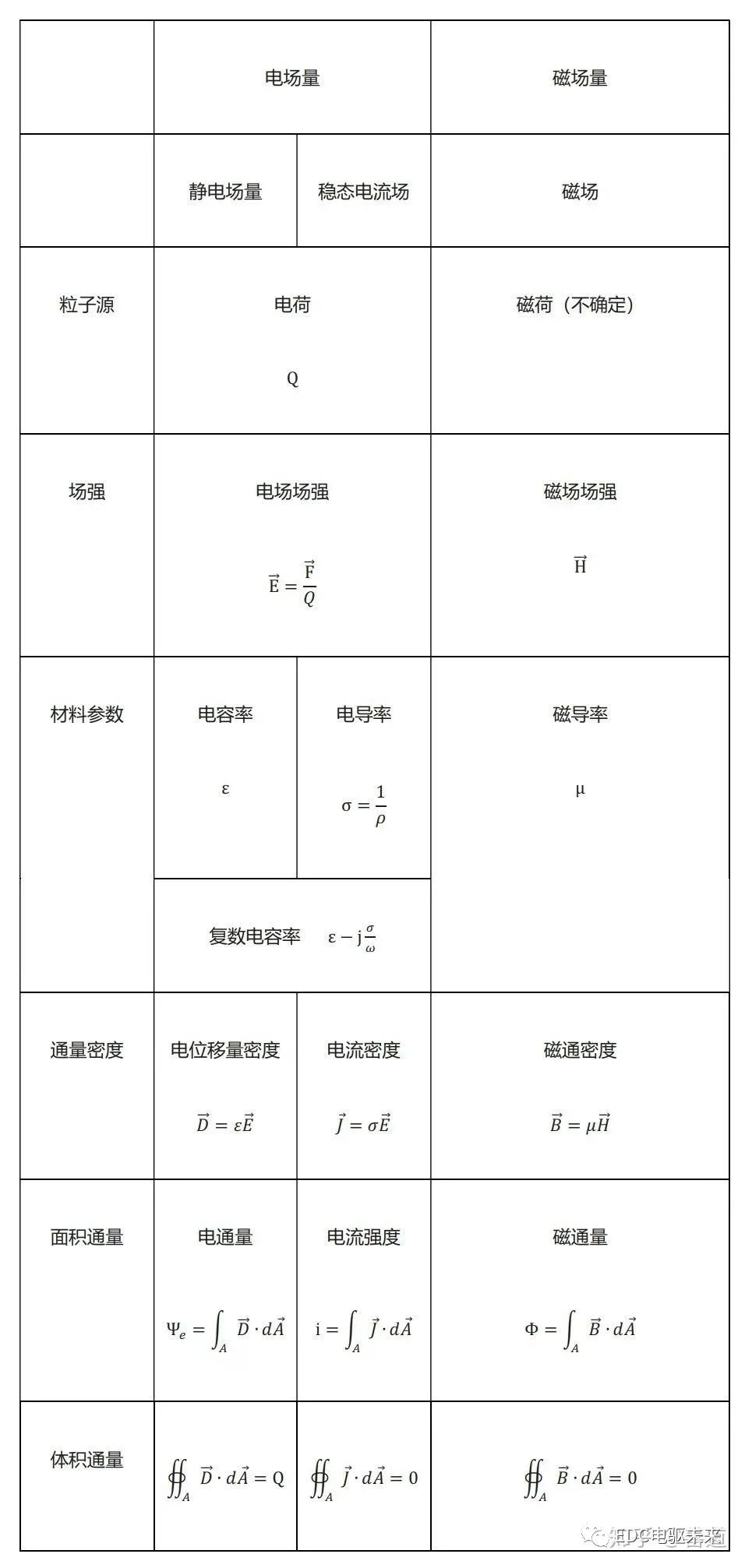
表1.1 電磁場中電磁關系

表1.2 電路網絡中的電磁關系

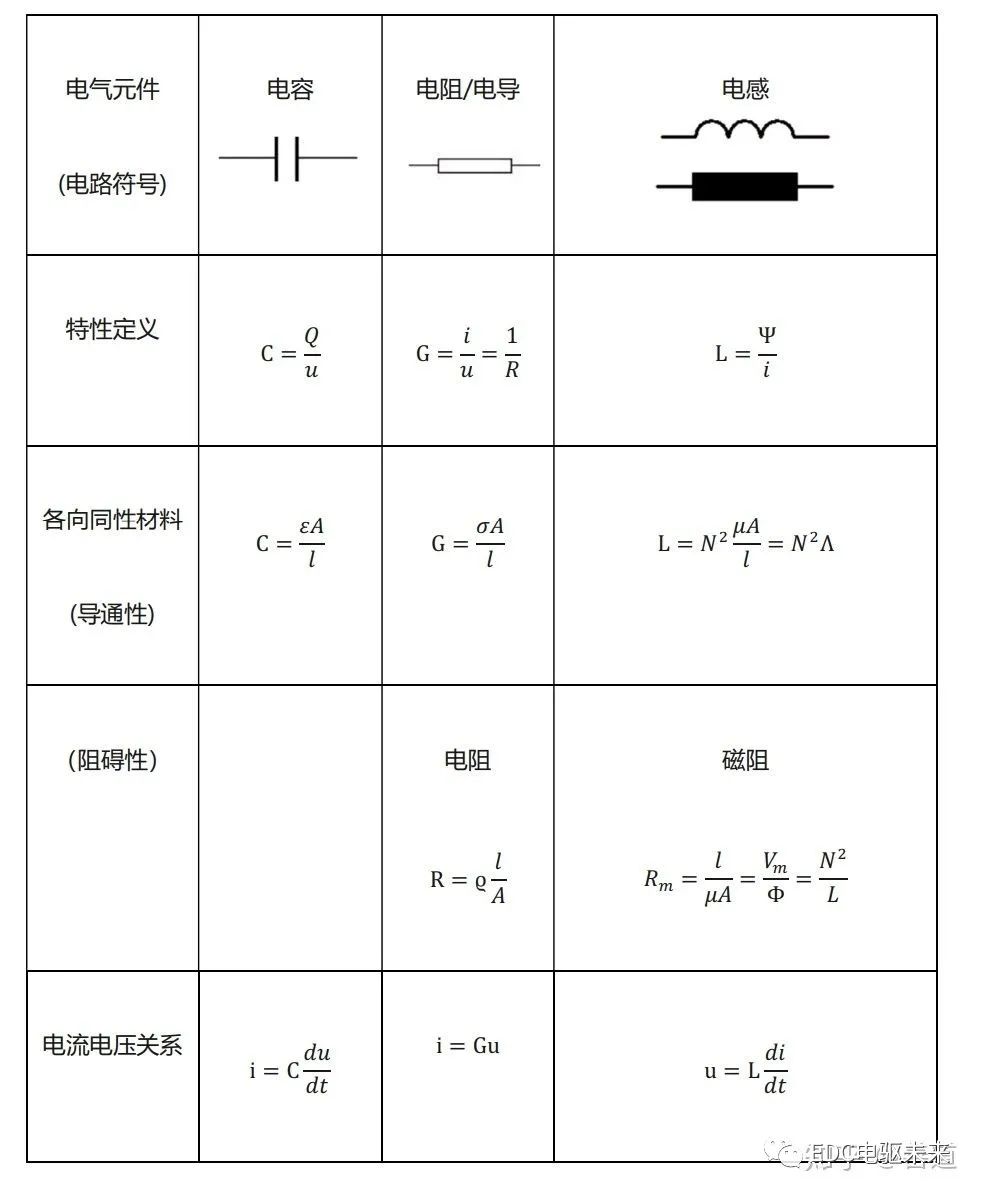
表1.3 電路中的電磁關系

編輯：黃飛