針對三相LCL型光伏并網(wǎng)逆變系統(tǒng)中，直接功率控制(DPC)開關(guān)頻率不固定、電流閉環(huán)控制動態(tài)響應(yīng)慢的缺點，本文提出一種內(nèi)環(huán)采用電流控制、外環(huán)采用功率控制的準(zhǔn)DPC 方法，兼顧DPC和電流控制的優(yōu)點，且具有動態(tài)響應(yīng)快、開關(guān)頻率固定和電流正弦度高的優(yōu)點。通過在Matlab/Simulink 中搭建控制系統(tǒng)仿真模型，結(jié)果表明該控制策略具有一定的可行性。

1

LCL型濾波器的三相并網(wǎng)逆變器模型

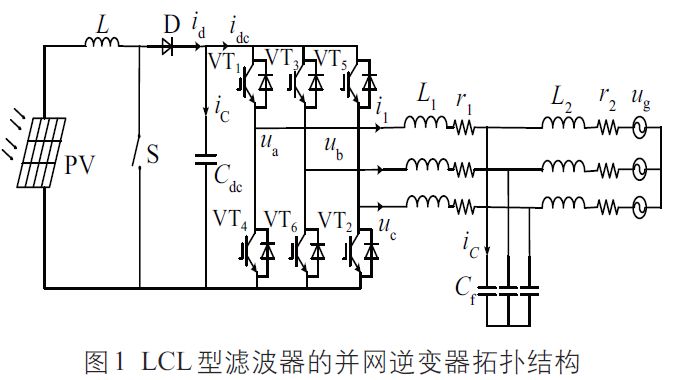
圖1 為采用LCL 型濾波器的三相光伏并網(wǎng)發(fā)電系統(tǒng)的拓?fù)浣Y(jié)構(gòu)。三相并網(wǎng)逆變器主電路包括輸入直流母線濾波電容C、6 個絕緣槽雙極型大功率晶體管(IGBT)開關(guān)管組成的三相全橋電路，以及由濾波電感L1 、L2 和濾波電容Cf 組成的三階濾波器。圖1 中，u、i 分別為電壓、電流；id 為二極管D 的電流；VT 為晶閘管；r1、r2 為濾波電感L1、L2 的內(nèi)阻；ug 為電網(wǎng)電壓；下標(biāo)dc 表示直流；下標(biāo)a、b、c 分別對應(yīng)逆變器的A、B、C 三相。

在三相電網(wǎng)電壓平衡的條件下，逆變器三相狀態(tài)方程為：

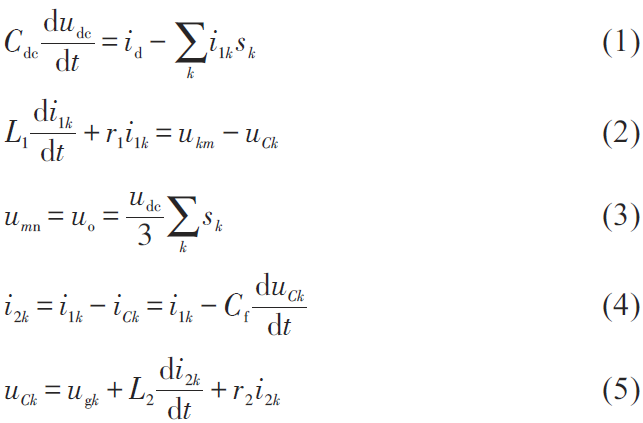
式中，下標(biāo)m=α、β ；下標(biāo)k=a，b，c； udc為光伏并網(wǎng)逆變器直流母線電壓； idc 為光伏并網(wǎng)逆變器直流側(cè)輸入電流； s 表示開關(guān)函數(shù)；下標(biāo)o 表示支路的開關(guān)狀態(tài)為開；下n 標(biāo)表示中性點處。

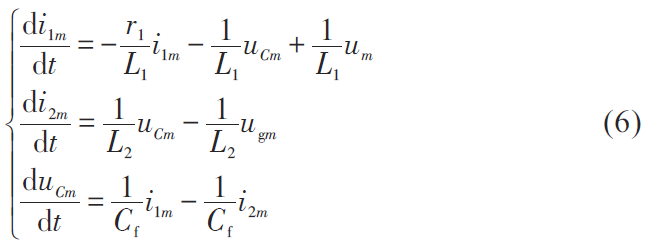
根據(jù)克拉克變換，可得到三相并網(wǎng)逆變器在αβ 坐標(biāo)系下的狀態(tài)方程為：

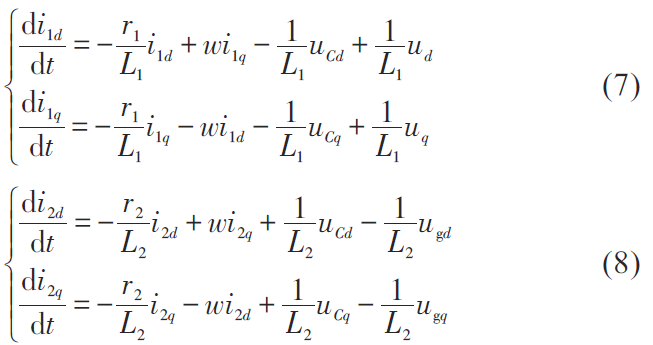
式中，w 為三相并網(wǎng)逆變器等效控制角頻率。

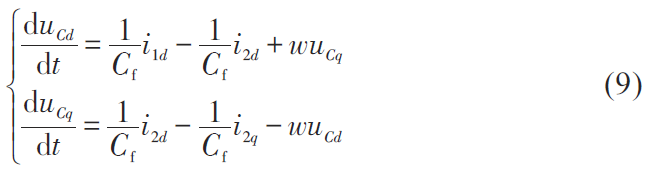
2

相并網(wǎng)逆變器控制策略模型的建立

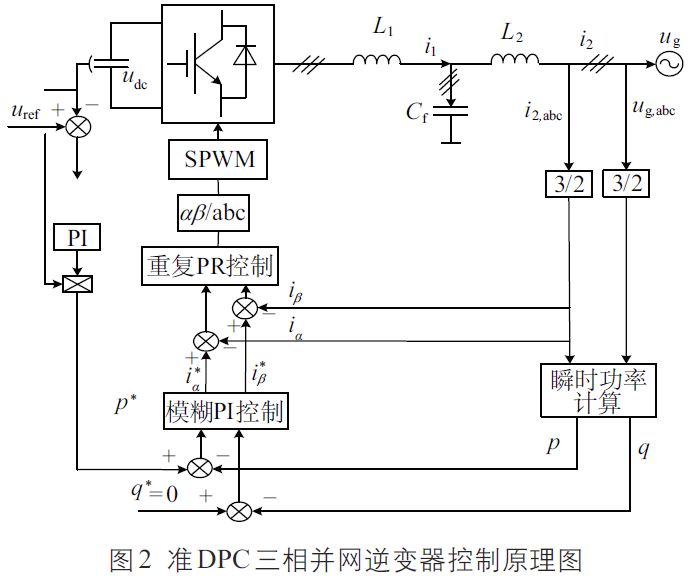
圖2 為準(zhǔn)DPC 三相并網(wǎng)逆變器控制原理圖，該系統(tǒng)主要由母線電壓控制、電流控制、功率控制等環(huán)節(jié)組成。其中外環(huán)采用一種基于模糊PI 的功率環(huán)控制策略，以實現(xiàn)對三相并網(wǎng)逆變器的功率控制；內(nèi)環(huán)采用一種重復(fù)PR 控制策略，以提高重復(fù)控制的動態(tài)性能和穩(wěn)定性，實現(xiàn)對三相并網(wǎng)逆變器的電流控制。其中， p* 為有功功率參考值，由輸入基準(zhǔn)電壓uref 與PI 控制的輸出乘積得到；無功功率參考值q* 設(shè)為零；上標(biāo)*表示參考值。

根據(jù)瞬時功率理論，可得到逆變器網(wǎng)側(cè)的復(fù)功率：

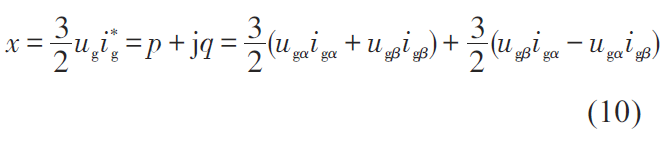
式中， ig 為電流矢量； ugα、ugβ 為αβ 坐標(biāo)系下電壓分量； igα、igβ 為αβ 坐標(biāo)系下電流分量。

功率控制器設(shè)計

光伏系統(tǒng)輸出功率是一個持續(xù)變化的量，當(dāng)光照資源、外界溫度、灰塵遮擋等外界條件變化時，輸出功率也在持續(xù)變化，而傳統(tǒng)的PI 控制方法并不能達(dá)到理想的控制效果。本文的功率控制器采用了一種基于模糊PI 的控制方法，運用Mamdani 模糊推理機制在線對PI 控制器參數(shù)進(jìn)行整定和優(yōu)化。圖3 為模糊PI 控制系統(tǒng)結(jié)構(gòu)圖。圖中， Δp/Δq 為輸入?yún)⒖加泄蜔o功誤差指令； ku 為比例因子； ke、ke′ 為量化因子； i*αβ 為αβ 坐標(biāo)下的系統(tǒng)并網(wǎng)電流參考值； e、e′ 分別為瞬時功率誤差和誤差變化率，本控制器將其量化在[-6，6]區(qū)間。

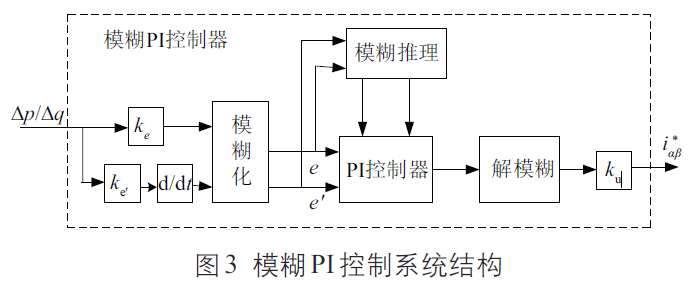
模糊PI 控制器首先會得到kp、ki 與e、e′之間的模糊關(guān)系， kp、ki 為PI 控制器參數(shù)，本控制器將其量化在[-3，3]區(qū)間；同時，在推理過程中會不斷檢測e 和e′，最后控制器依據(jù)推理規(guī)則對PID參數(shù)進(jìn)行實時整定, 以滿足變量e、e′ 對控制參數(shù)的不同要求，從而使功率控制器具有良好的動、靜態(tài)性能。

電流控制器設(shè)計

** 重復(fù)PR 控制系統(tǒng)模型**

文獻(xiàn)[11, 12]分別提出了逆變電源比例諧振控制方法和重復(fù)控制方法，但PR 控制對非線性負(fù)載中的高次諧波抑制能力差，而重復(fù)控制雖然其魯棒性較好，但缺點是動態(tài)性能較差。為解決以上問題，本文設(shè)計了一種基于比例諧振的重復(fù)控制系統(tǒng)，以改善控制器的性能。圖4 為重復(fù)PR控制系統(tǒng)結(jié)構(gòu)圖， z-N 為周期延時信號； Q(z) 為輔助補償值； Kr 為重復(fù)控制增益； S(z) 為受控對象補償值； d(z) 為非線性擾動量； P(z) 為逆變器等效數(shù)學(xué)模型。

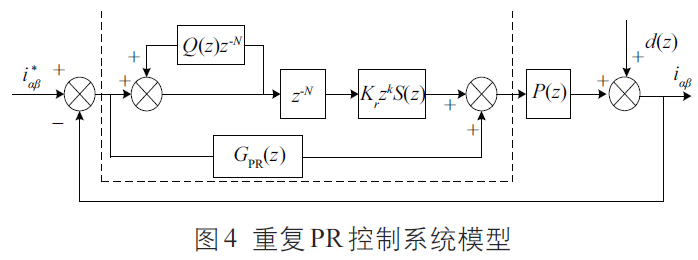
由圖4 可得出控制系統(tǒng)傳遞函數(shù)E(z) 為：

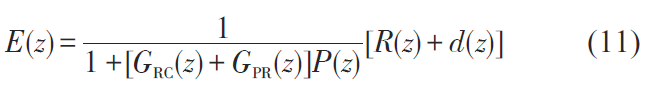
式中， G 為開環(huán)時逆變器傳輸函數(shù)；下標(biāo)RC 表示諧振控制器； R(z) 為z 傳遞矩陣諧振控制器傳輸函數(shù)。

再令誤差傳遞函數(shù)為：

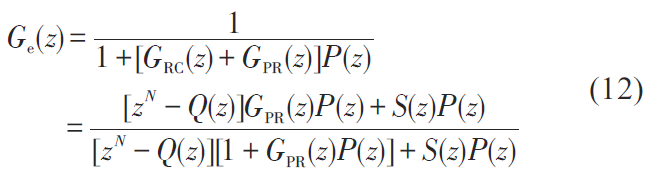
繼而可得到特征多項式y(tǒng) ：

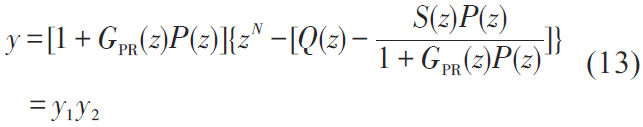
由式(13)可知，當(dāng)特征多項式的兩個特征根在單位圓內(nèi)時，即可以保持控制系統(tǒng)的穩(wěn)定性。

** 重復(fù)PR 控制器設(shè)計**

由以上分析可知，當(dāng)控制器參數(shù)在單獨的PR系統(tǒng)穩(wěn)定范圍內(nèi)選擇時，控制系統(tǒng)才會達(dá)到穩(wěn)定。因此，對PR 控制器的兩個參數(shù)需進(jìn)行單獨設(shè)計。kp 為比例增益， kp 的取值會影響控制系統(tǒng)的抗干擾能力和穩(wěn)態(tài)性能，因此取值需要適中，不能過大也不能太小。取值太小會使系統(tǒng)中電流諧波分量變大，降低系統(tǒng)的抗干擾能力；而取值太大會降低系統(tǒng)的幅值裕度。文獻(xiàn)[13]中對該問題進(jìn)行了建模和仿真分析，當(dāng)kp =0.07 時，控制系統(tǒng)可得到很好的控制效果。

ki 為積分增益，對控制的增益有影響。ki 值較大時，控制器的靜態(tài)誤差會較快衰減，但會影響系統(tǒng)的相位裕度，使其變小；當(dāng)ki 值較小時，會難以消除系統(tǒng)的靜態(tài)誤差，從而影響系統(tǒng)的控制精度。

本文對ki 分別為50、80、100、120 時的控制系統(tǒng)進(jìn)行了仿真分析( kp 值固定)，圖5 為被控對象PR 控制波德圖。

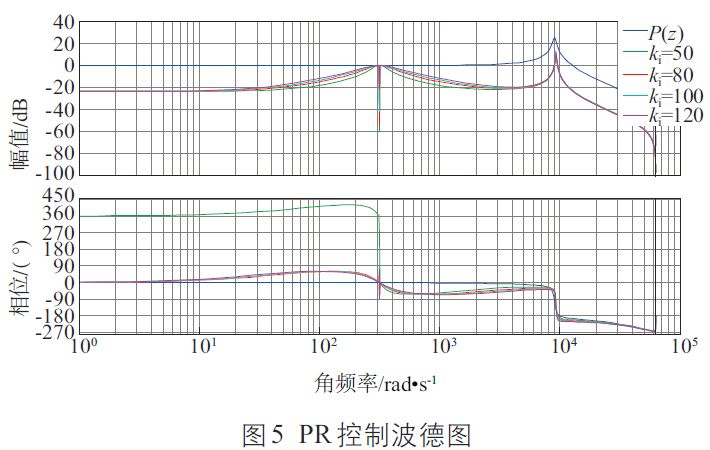
由圖5 可知，當(dāng)ki 為50 和120 時，相位裕度均難以滿足系統(tǒng)穩(wěn)定性的要求。而當(dāng)ki =80時，系統(tǒng)相位裕度較好，可獲得較好的控制效果。

重復(fù)PR 控制的控制對象等效為：

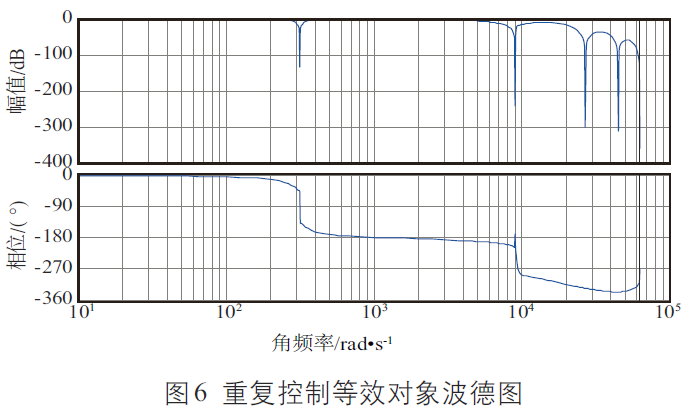
圖6 為重復(fù)PR 控制中重復(fù)控制等效對象波德圖。由圖6 可知，等效控制對象中低頻段的增益基本為零，但在角頻率w=9260 rad/s 處，出現(xiàn)了高頻諧振，諧振峰值為31.2 dB，這是由于逆變器中LCL 濾波器的諧振問題所致。因此，如果對控制器不采取抑制措施，會使諧振頻率幅值變大，從而使輸出電壓發(fā)生波形畸變。此外，系統(tǒng)在高頻段處，系統(tǒng)諧波的衰減能力也非常有限，對諧波的抑制能力也會變差。

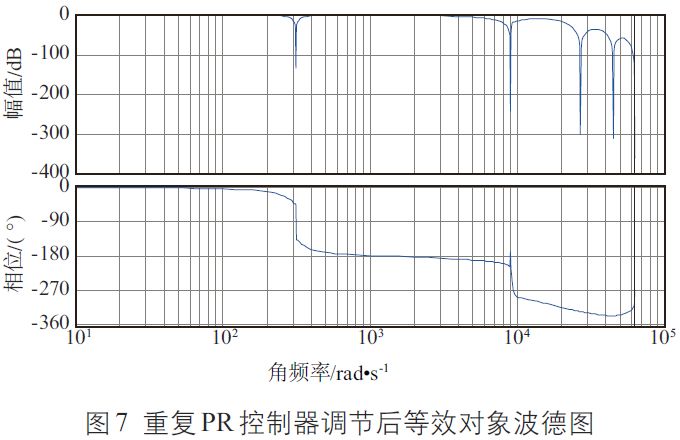
圖7 為經(jīng)過重復(fù)PR 控制器調(diào)節(jié)后的等效對象波德圖。由圖7 可知，經(jīng)過重復(fù)PR 控制器的調(diào)節(jié)，消除了圖6 中的高頻諧振，同時，等效控制對象中低頻增益變?yōu)?。而且，等效控制對象中的高頻段得到了迅速衰減，從而使控制系統(tǒng)具有良好的抗擾動能力，系統(tǒng)穩(wěn)定性變好。

3

系統(tǒng)仿真分析

為驗證本文所提出的電流內(nèi)環(huán)和功率外環(huán)控制策略的有效性，按照圖2 的拓?fù)浣Y(jié)構(gòu)在Matlab/Simulink 仿真環(huán)境中搭建了LCL 型光伏逆變系統(tǒng)的仿真模型，并采用以上控制策略進(jìn)行控制。控制系統(tǒng)參數(shù)為：并網(wǎng)逆變器額定功率為2kW， fk =12.5 kHz，開關(guān)頻率fs =20 kHz， Cdc =2000 μF， L1 =8 mH， L2 =2 mH， Cf =10 μF，等效
電阻為0.8 Ω。

圖8 為采用本文設(shè)計的控制策略時，并網(wǎng)逆變系統(tǒng)有功功率和無功功率的仿真波形。由圖8可知，當(dāng)控制系統(tǒng)功率環(huán)采用模糊PI 控制系統(tǒng)時，系統(tǒng)有功功率可在很短時間內(nèi)達(dá)到給定值，調(diào)整過程非常迅速，當(dāng)系統(tǒng)達(dá)到穩(wěn)定后，有功功率波動非常小，而無功功率也基本保持在零。

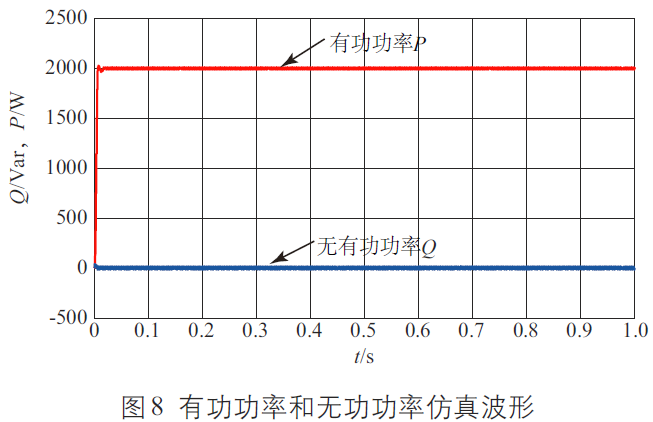
圖9 為三相并網(wǎng)電流波形，仿真時間為0.2 s。由圖9 可知，并網(wǎng)電流可在一個周期內(nèi)迅速達(dá)到穩(wěn)定，動態(tài)響應(yīng)速度很快，且正弦度較好。

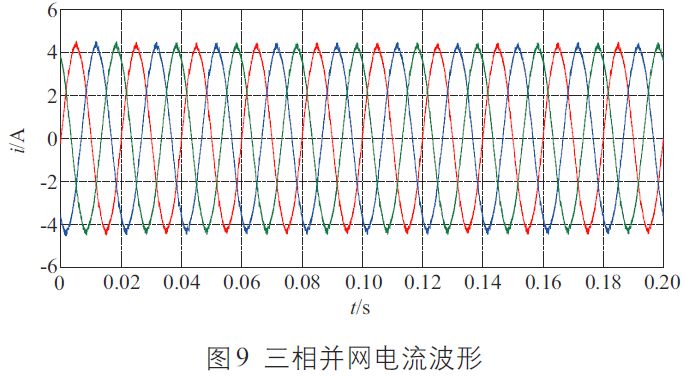
圖10 為并網(wǎng)電流諧波頻譜分布圖。由圖10可知，并網(wǎng)電流頻譜分布集中，通過對電流的諧波分析，電流的THD=1.98%，滿足并網(wǎng)要求。

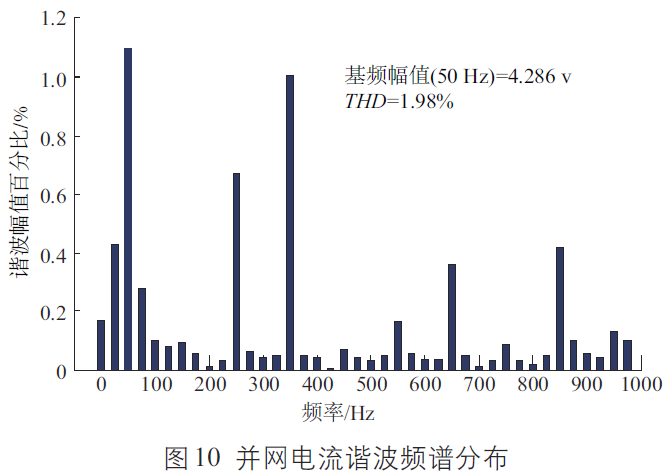
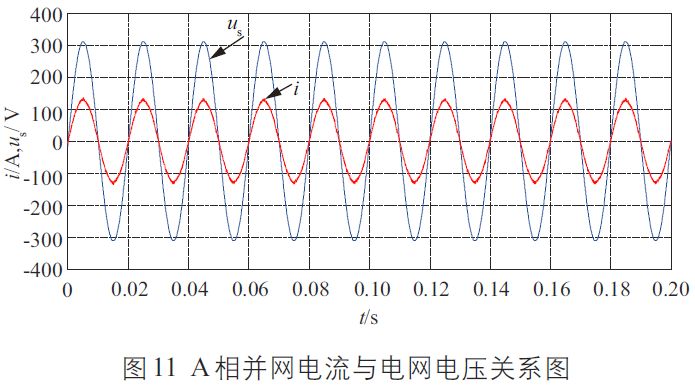
圖11 為系統(tǒng)滿載運行時，A 相并網(wǎng)電流與電網(wǎng)電壓關(guān)系圖(其中，電流放大30 倍)。由圖11 可知，并網(wǎng)電流與相應(yīng)的電網(wǎng)電壓同頻、同相位，實現(xiàn)了光伏逆變器單位功率因數(shù)并網(wǎng)運行。

4

結(jié)論

本文通過對三相LCL 型并網(wǎng)逆變器的拓?fù)浞治觯O(shè)計了一種內(nèi)環(huán)采用電流控制、外環(huán)采用功率控制的準(zhǔn)DPC 方法，兼顧了DPC 和電流控制的優(yōu)點，實現(xiàn)了對有功和無功的良好控制；并在Matlab/Simulink 中搭建控制系統(tǒng)仿真模型，結(jié)果表明，該種控制策略是可行的。