1. 相機模型
相機將三維世界中的坐標點(單位為米)映射到二維圖像平面(單位為像素)的過程能夠用一個幾何模型進行描述。這類模型有很多種,其中最簡單的稱為針孔模型。針孔模型是很常用,而且有效的模型,它描述了一束光線通過針孔之后,在針孔背面投影成像的關系。同時,由于相機鏡頭上的透鏡的存在,會使得光線投影到成像平面的過程中會產生畸變。因此,我們使用針孔和畸變兩個模型來描述整個投影過程。
1.1 針孔相機模型
在物理課堂上,我們可能都見過一個蠟燭投影實驗:在一個暗箱的前方放著一支點燃的蠟燭,蠟燭的光透過暗箱上的一個小孔投影在暗箱的后方平面上,并在這個平面上形成了一個倒立的蠟燭圖像。在這個過程中,針孔模型能夠把三維世界中的蠟燭投影到個二維成像平面。
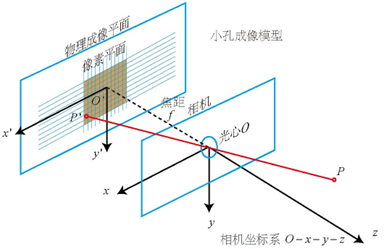
圖1:針孔相機模型
如圖1所示,來對這個簡單的針孔相機模型進行幾何建模。設O-x-y-z為相機坐標系,習慣我們讓z軸指向相機前方,x向右,y向下,O為攝像機的光心,也是針孔模型中的針孔。
P為相機坐標系下的一點,經過小孔O投影之后,落在物理成像平面O′-x′-y′上,成像點為P′,并且設物理成像平面到小孔的距離為f(焦距)。
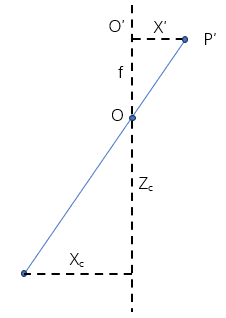
圖2:針孔相機模型的三角形關系
那么,如圖2所示,根據三角形相似關系,有
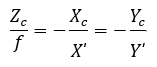
上式中,負號表示成的像是倒立的。
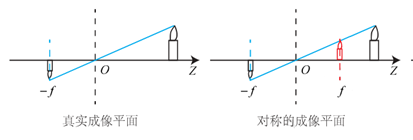
圖3:針孔模型的簡化
為了簡化模型,如圖3所示,我們把可以成像平面對稱到相機前方,和三維空間點一起放在攝像機坐標系的同一側,這樣做可以把公式中的負號去掉,使公式更加簡潔:
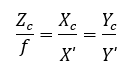
把成像平面放在攝像機坐標系的同一側,這是一種我們處理真實世界與相機投影的數學手段,并且,大多數相機輸出的圖像并不是倒像,相機自身的軟件會幫你翻轉這張圖像,所以你看到的一般是正著的像,也就是對稱的成像平面上的像。所以,盡管從物理原理來說,小孔成像應該是倒像,但由于我們對圖像作了預處理,所以理解成在對稱平面上的像,并不會有影響。
整理后得到:
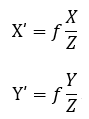
上面兩式描述了點P和它的像P′之間的空間關系。
1.2 各個坐標系的定義
以被測物體上的點作為參考,定義的絕對坐標系,是一個三維直角坐標系,以其為基準可以描述相機和待測物體的空間位置,單位是米。
2)相機坐標系(camera coordinate)
以相機光心為坐標原點,主光軸上物體方朝焦點方向為z軸,平行于sensor平面的兩條垂直邊分別為x和y軸,單位是米。
3)圖像坐標系(film coordinate)
以主光軸與sensor的交點為坐標原點,平行于sensor平面的兩條垂直邊分別為x和y軸,這個平面是建立在實際成像面上的,是個二維坐標系,單位是毫米。
4)像素坐標系(pixel coordinate):
平行于sensor的虛擬成像平面,左上角頂點為原點,x軸和y軸都平行于圖像平面,以像素為單位。
1.3 坐標系轉換
1.3.1 從世界坐標系到相機坐標系
由于相機在運動,所以點P的相機坐標Pc應該是它的世界坐標Pw,根據相機的當前位姿,變換到相機坐標系下的結果。相機的位姿由它的旋轉矩陣R和平移向量t來描述。那么有
剛體變換公式為
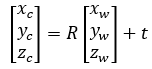
齊次坐標形式為
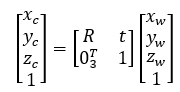
1.3.2 從相機坐標系到圖像坐標系
從相機坐標系到圖像坐標系就是直接運用針孔成像原理。
齊次坐標形式為
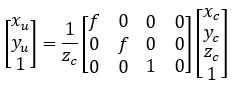
1.3.3 從圖像坐標系到像素坐標系
像素坐標系通常的定義方式是:原點o′位于圖像的左上角,u軸向右與x軸平行,v軸向下與y軸平行。像素坐標系與成像平面之間,相差了一個縮放和一個原點的平移。
用數學式表達如下
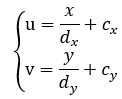
齊次坐標形式為
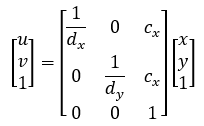
dx,dy:表示圖像單個像素的寬和高,單位為mm/pixel;
(cx,cy):表示圖像中心點的像素坐標,即主光軸與sensor平面的交點。
1.3.4 從相機坐標系到像素坐標系
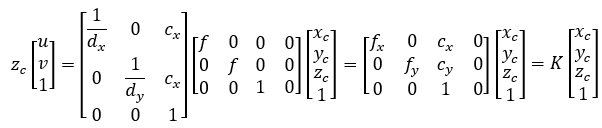
上式中,
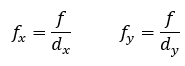
其中,fx、fy的單位為像素。
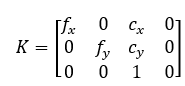
我們把中間的量組成的矩陣稱為相機的內參數矩陣K。
通常認為,相機的內參在出廠之后是固定的,不會在使用過程中發生變化。有的相機生產廠商會告訴你相機的內參,而有時需要你自己確定相機的內參,也就是標定。
1.3.5從世界坐標系到像素坐標系
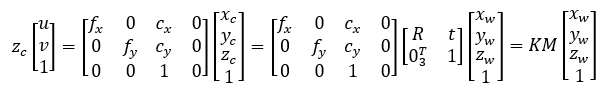
其中
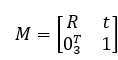
我們把旋轉矩陣R和平移向量t組成的矩陣稱為相機的外參數矩陣M。
相比于不變的內參,外參會隨著相機運動發生改變。
內參K與外參M的乘積,是一個3×4的矩陣,稱為投影矩陣,該矩陣可體現任意空間點的圖像像素坐標與世界坐標之間的關系。
通過從世界坐標系到像素坐標系的公式可知,若已知投影矩陣和空間點世界坐標,則可求得空間點的像素坐標,因此,在線性模型中,一個物點在成像平面上對應唯一的像點。但反過來,若已知像素坐標和投影矩陣,代入以上公式,只能得到關于空間點世界坐標的兩個線性方程,這兩個線性方程表示的是像點和光心的連線,即連線上所有點都對應著該像點,由此可知,在線性模型中,一個像點對應的物點并不具有唯一性,因此,只通過一幅圖像對圖像場景進行三維重建是不現實的。
1.3.6 齊次坐標
為了描述人眼對物體有“近大遠小”的處理(視角),也就是投影透視,便引入齊次坐標來描述。簡單地說,齊次坐標是用N+1維去描述一個N維的坐標。
齊次坐標與笛卡爾坐標的轉化關系:
笛卡爾坐標:(x/w, y/w)——齊次坐標:(x, y, w)
假如齊次坐標系下的坐標為(1,3, 5),那么,轉換到笛卡爾坐標系下的坐標即為(1/5, 3/5);同理,假如齊次坐標系下的坐標為(2, 6, 10),那么轉換到笛卡爾坐標系下的坐標即為(2/10, 6/10),化簡后其值仍為(1/5, 3/5)……于是我們就可以知道:對于這個例子來說,齊次坐標系下任何形式為(1a,3a, 5a)的坐標(a不為0)在笛卡爾坐標系下都代表著同一個坐標(1/5, 3/5),類似地,便有了“齊次”的說法,由此也引出了齊次坐標的“伸縮不變性”。
用齊次坐標進行仿射幾何變換
現在,我們用笛卡爾坐標定義兩條直線:
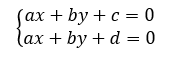
在這種情況下,這兩條直線不可能相交。
轉換到齊次坐標表示為
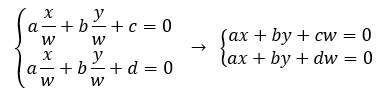
此時,w=0時有解,其交點為(x, y, 0),同時,w=0表示這個點在無窮遠處,于是兩條平行線在無窮遠處可相交。
齊次坐標在圖形學和計算機視覺中是一個很重要的概念,一方面是因為它更易于進行仿射幾何變換,另一方面也能夠用來明確區分向量和點。
用齊次坐標區分向量和點
假設我們在齊次坐標系下找到了這樣一組基:
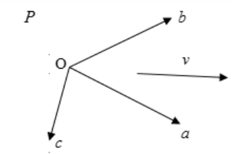
圖4
于是,我們可以找到一組系數(v1,v2, v3),將向量v表示成:
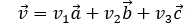
對于齊次坐標系下的一個點p,可以表示成位置向量
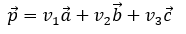
將上面兩個式子均寫成齊次坐標系下的矩陣形式:
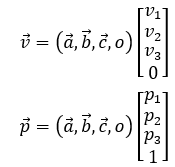
我們可以看到,(a,b,c,o)為坐標基矩陣,右側列向量分別為向量v和點p在齊次坐標系下的坐標。于是,若想在齊次坐標系下的三維坐標中表示向量,則第四項系數為0,若想表示點,則第四項系數為1,這樣就可以很方便地區分出點或者向量了。
1.4 畸變模型
為了獲得好的成像效果,我們在相機的前方加了透鏡。透鏡的加入對成像過程中光線的傳播會產生新的影響:一是透鏡自身的形狀對光線傳播的影響,二是在機械組裝過程中,透鏡和成像平面不可能完全平行,這也會使得光線穿過透鏡投影到成像面時的位置發生變化。
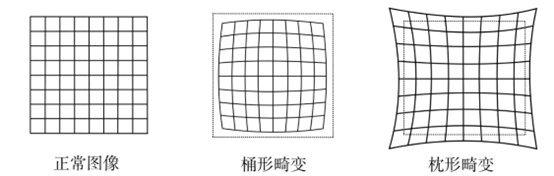
圖5:畸變
在針孔模型中,一條直線投影到像素平面上還是一條直線。可是,在實際拍攝的照片中,攝像機的透鏡往往使得真實環境中的一條直線在圖片中變成了曲線。越靠近圖像的邊緣,這種現象越明顯。由于實際加工制作的透鏡往往是中心對稱的,這使得不規則的畸變通常徑向對稱。它們主要分為兩大類,桶形畸變和枕形畸變。
桶形畸變是由于圖像放大率隨著離光軸的距離增加而減小,而枕形畸變卻恰好相反。
在這兩種畸變中,穿過圖像中心和光軸有交點的直線還能保持形狀不變。
除了透鏡的形狀會引入徑向畸變外,在相機的組裝過程中由于不能使得透鏡和成像面嚴格平行也會引入切向畸變。
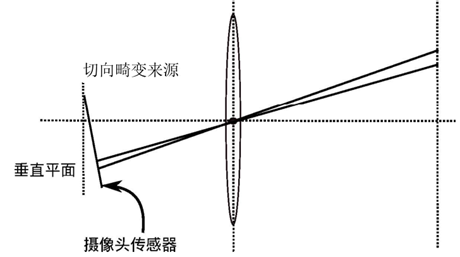
圖6:切向畸變來源示意圖
為更好地理解徑向畸變和切向畸變,可以用更嚴格的數學形式對兩者進行描述。我們知道平面上的任意一點p可以用笛卡爾坐標表示為[x,y]T,也可以把它寫成極坐標的形式[r,θ]T,其中r表示點p離坐標系原點的距離,θ表示和水平軸的夾角。徑向畸變可看成,坐標點沿著長度方向發生了變化δr,也就是其距離原點的長度發生了變化。切向畸變可以看成坐標點沿著切線方向發生了變化,也就是水平夾角發生了變化δθ。
對于徑向畸變,無論是桶形畸變還是枕形畸變,由于它們都是隨著離中心的距離增加而增加。我們可以用一個多項式函數來描述畸變前后的坐標變化:這類畸變可以用和距中心距離有關的二次及高次多項式函數進行校正:
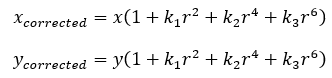
其中[x,y]T是未校正的點的坐標,[xcorrected,ycorrected]T是校正后的點的坐標,注意它們都是歸一化平面上的點,而不是像素平面上的點。
在校正模型中,對于畸變較小的圖像中心區域,畸變校正主要是k1起作用。而對于畸變較大的邊緣區域主要是k2起作用。普通攝像頭用這兩個系數就能很好的校正徑向畸變。對畸變很大的攝像頭,比如魚眼鏡頭,可以加入k3畸變項對畸變進行校正。
另一方面,對于切向畸變,可以使用另外的兩個參數p1,p2來進行校正:
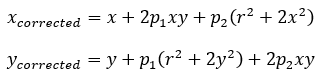
因此,聯合上面兩式,對于相機坐標系中的一點P(X,Y,Z),我們能夠通過五個畸變系數找到這個點在像素平面上的正確位置:
(1)將三維空間點投影到歸一化圖像平面。設它的歸一化坐標為[x,y]T
(2)對歸一化平面上的點進行徑向畸變和切向畸變校正。
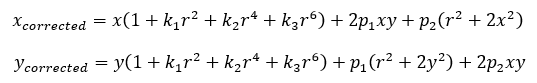
(3)將校正后的點通過內參數矩陣投影到像素平面,得到該點在圖像上的正確位置。
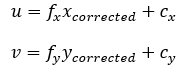
在上面的校正畸變的過程中,我們使用了五個畸變項。實際應用中,可以靈活選擇校正模型,比如只選擇k1,p1,p2這三項等。
1.5標定建模
綜合以上描述的內容,我們可以把相機的成像模型,或者說相機標定的數學模型看成一個理想的模型加一個誤差模型,理想模型就是針孔相機模型,誤差模型就是畸變引起的一個誤差。
結合針孔相機模型+鏡頭畸變,那么相機標定模型的建立過程如圖7所示:

圖7:標定建模的過程(坐標系轉換)
標定數學模型為:
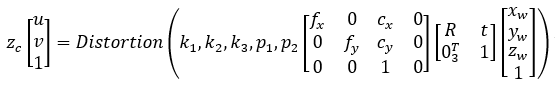
整個流程的總結:世界坐標系中的一點,通過剛體變換到相機坐標系下,再通過針孔成像的原理變換到圖像坐標系,然后歸一化到單位焦平面上去做去畸變處理,最后就是把圖像進行數字化處理,轉化到像素坐標系上。
1.6標定算法
標定算法的基本思路是在較高精度的2D-3D對應點基礎上,先采用DLT或張正友方法求初值,然后非線性優化迭代求解精確解。
1.6.1直接線性標定法DLT
Abdel-Aziz和Karara于20世紀70年代初提出了直接線性變換DLT(direct linear transformation)的攝像機標定方法,這種方法忽略攝像機畸變引起的誤差,直接利用線性成像模型,通過求解線性方程組得到攝像機的參數。
DLT方法的優點是計算速度很快,操作簡單且易實現;缺點是由于沒有考慮攝像機鏡頭的畸變,因此不適合畸變系數很大的鏡頭,否則會帶來很大誤差。
DLT標定法需要將一個特制的立方體標定模板放置在所需標定攝像機前,其中標定模板上的標定點相對于世界坐標系的位置已知。
首先,由立體標定參照物圖像求取投影矩陣的算法,公式如下:

上式中,(Xwi,Ywi,Zwi)為空間第i個點的坐標;(ui,vi)為第i個點的圖像坐標;mij為空間任意一點投影矩陣的第i行j列元素。
從上式可以得到三組線性方程,
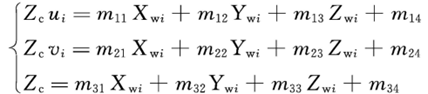
將上式方程消去Zc得到兩個關于mij的線性方程。
這個式子表明,如果在三維空間中,已知n個標定點,其中各標定點的空間坐標為(Xwi,Ywi,Zwi),圖像坐標為(ui,vi)(i=1,…,n),則可得到2n個關于M矩陣元素的線性方程,且該2n個線性方程可以用下面所示的矩陣形式來表示。
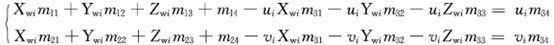
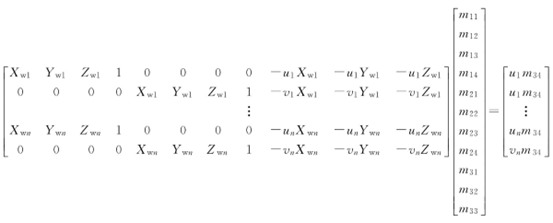
由此可見,投影矩陣乘以任意不為零的常數并不影響(Xwi,Ywi,Zwi)與(ui,vi)的關系,因此,假設m34=1,從而得到關于M矩陣其他元素的2n個線性方程,其中線性方程中包含11個未知量,并將未知量用向量表示,即11維向量m,化簡得到:
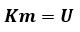
K、U為已知向量。當2n>11時,利用最小二乘法對上述線性方程進行求解:
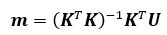
若已知空間中至少6個已知點和與之對應的圖像點坐標,便可求得投影矩陣。一般采用在標定的參照物上選取個數多于6個已知點,使方程的個數遠遠超過未知量的個數,從而降低用最小二乘法求解造成的誤差。
1.6.2張正友標定法
張正友標定法,也稱Zhang標定法,是由微軟研究院的張正友博士于1998年提出的一種介于傳統標定方法和自標定方法之間的平面標定法。它既避免了傳統標定方法設備要求高、操作繁瑣等缺點,又比自標定的精度高、魯棒性好。

圖8:黑白格標定板
張正友標定法的主要步驟如下:
1)一張貼在一塊剛性平面上的黑白棋盤方格圖案的標定板;
2)移動標定板或者相機,從不同角度拍攝若干照片(理論上照片越多,誤差越小);
3)對每張照片中的角點進行檢測,確定角點的圖像坐標與實際坐標;
4)在不考慮徑向畸變的前提下,即采用相機的線性模型。根據旋轉矩陣的正交性,通過求解線性方程,獲得攝像機的內部參數和第一幅圖的外部參數;
5)利用最小二乘法估算相機的徑向畸變系數;
6)根據再投影誤差最小準則,對內外參數進行優化。
張正友標定法原理簡介
假設我們提供K個棋盤圖像,每個棋盤有N個角點,于是我們擁有2KN個約束方程。與此同時,忽略畸變的情況下,我們就需要求解4個內參和6K個外參(內參只于相機內部參數有關,外參卻隨目標點位置變化而變化),也就是說,只有當2KN≥4+6K的時候,也即K(N-3) ≥2時,才能求出內外參矩陣。同時,無論在一張棋盤上檢測到多少角點,由于棋盤上角點的規則布置使得真正能利用上的角點只有4個(在四個方向上可延展成不同的矩形),于是有當N=4時,K(4-3) ≥2,即K≥2,也就是說,我們至少需要兩張棋盤格在不同方位的圖像才能求解出無畸變條件下的內參和外參。
實際上,我們往往會在一張棋盤格上布置更多的角點,因為這樣就可以通過最小二乘法求得最優解了,同樣地,我們會需要至少10張以上的棋盤格圖像,目的是考慮數值穩定性和提高信噪比,得到更高質量的結果。
與此同時,我們在這里引入單應性的概念。在計算機視覺中的單應性被定義為從一個平面到另一個平面的投影映射關系。
我們定義相機標定的單應性矩陣(從物體平面到成像平面)為:
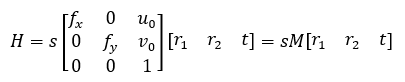
這里引入的s為任意尺度的比例系數。單應性矩陣描述了物體在世界坐標系和像素坐標系之間的相對位置關系(包含了內參和外參)。
若已知標定板上的點在空間和圖像上的坐標,即可求解單應性矩陣,且每幅模板對應一個單應矩陣。
1.7標定板
標定算法中我們需要一些可靠的樣本點,這些樣本點由世界坐標系中的3D點和其在圖像上的2D像點組成,用這些2D和3D點對來求解標定參數。
為了構建更高精度的3D和2D點,就需要使用標定板。
1.7.1標定板的基本要求
1)標定板的精度(平整度):3D點要求是共面的,標定點的坐標精度是準確的。
2)標定板的穩定性:降低溫度膨脹系數。標定板的材質溫度膨脹系數要盡可能小。
3)標定板的均勻性(背光源):要求標定板有背光的原因是盡量減少圖像受環境光的干擾。
1.7.2pattern設計要求
1)便于特征點提取(如角點或圓心);
2)特征點的坐標無歧義,比如對于棋盤格這種有規律的pattern,要求棋盤格圖像整體的大小不要充滿整個圖像,比如只占拍攝圖像的1/2。

圖9:標定板
1.7.3標定板對標定精度的影響
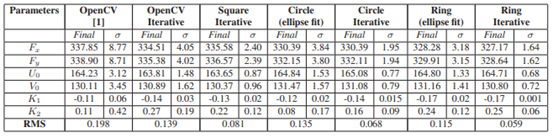
圖10:標定精度的對比
一般來講,圓形(圓環)標定板的提取精度高于棋盤格的提取精度。主要原因是對于棋盤格來講,邊緣位置在實際相機所拍攝的圖像來看,受到光的影響和sensor本身噪聲影響,所得到的灰度可能會有明暗差別,導致計算棋盤格角點位置的時候會有誤差。而圓形或圓環的擬合中,半徑多一點或少一點,對于圓心位置的計算影響相對較小。
1.8標定步驟
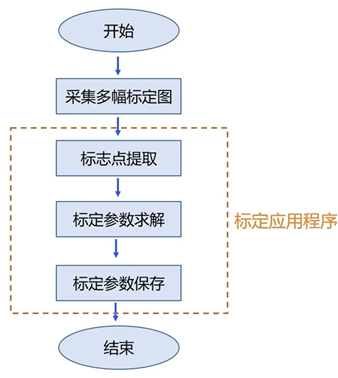
圖11:標定步驟
審核編輯:黃飛
?
 電子發燒友App
電子發燒友App

























評論