matlab最優化實驗
6.1知識要點與背景
6.1.1 由簡入繁: 最佳水槽斷面問題的推廣
?????
6.1.2 微分法求最大和最小
??????? ◆問題4????? (1)求受檢點: ,
?zxy6_1.m
【??? syms x1 x2????????????????????????????????????????? %定義符號變量。
f=x1^3-x2^3+3*x1^2+3*x2^2-9*x1;?? % 函數z。
v=[x1 x2];df=jacobian(f,v)??????????????? %計算雅可比 。?
[X,Y]=solve(df(1),df(2));[X,Y]???????? % 用指令solve求駐點。???????????? 】
??????
?zxy6_2.m
【??? clf,xmin=-5;xmax=3.5;ymin=-3;ymax=5;
x1=linspace(xmin,xmax,30);x2=linspace(ymin,ymax,30);
[X1,X2]=meshgrid(x1,x2);Z= X1.^3.-X2.^3+3*X1.^2+3*X2.^2-9*X1;
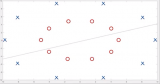
contour(X1,X2,Z,60);,hold on,? xp=[-3,1,-3,1];yp=[0 0 2 2];
plot(xp,yp,'ro'),axis([xmin xmax ymin ymax]),colorbar
xlabel('x_1'),ylabel('x_2'),
for i=1:length(xp)
? text(xp(i),yp(i),['\leftarrow (',num2str(xp(i)),',',num2str(yp(i)),')'] )
?????? end????????????? 】
??????
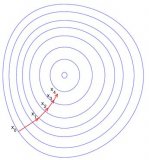
?6.2? 實驗與觀察(Ⅰ):模擬盲人下山的迭代尋優法
zxy6_3.m(盲人下山的模擬)
【????? clf, a=-2;b=4;
xmin=a;xmax=b;ymin=a;ymax=b;??? %設置變量范圍和坐標軸顯示范圍。
x1=linspace(xmin,xmax,100);x2=linspace(ymin,ymax,100);
[X1,X2]=meshgrid(x1,x2);
[Z,DZ1,DZ2]=zxy6_3f(X1,X2); %計算函數和梯度向量。
contour(X1,X2,Z,30),?????????????? %畫等值線圖。
axis([xmin xmax ymin ymax]),hold on,
axis equal,????????????????????????????? %該命令將使橫軸、縱軸具有相同比例,避免失真。
plot([1.46808510638298],[1.148936170212776],'o'),? %標注最優點。
axis([xmin xmax ymin ymax])?????????????
x=[];y=[];??????????? %開始用鼠標選點,按左鍵選點,按右鍵中止選點過程。
disp('Select a point by put on mouse left-key')??????
????????????????????????????? %disp指令,在命令窗口顯示文字。
disp('Stop selecting point by put on mouse right-key')
button=1;???????? %button和ginput命令結合使用可用鼠標選點, 按左鍵時button=1。
x=[];y=[];
while button==1???????????????
? [xi,yi,button]=ginput(1);
???????????????????? %ginput(n)用鼠標選n個點,xi,yi分別為點的橫坐標和縱坐標。
?? plot([xi],[yi],'r.','MarkerSize',10),hold on,???????????? %畫所選的點。?
?? [zi,dz1,dz2]=zxy6_3f(xi,yi);?????????????????????? %計算函數值和梯度方向。
?? v=zi;
?? contour(X1,X2,Z,[v v],'-'),???????????? %在點所在的高度畫一條等高線。???
?? axis([xmin xmax ymin ymax]),
?? x=[x,xi];y=[y,yi];??????
?? H_line2=plot(x,y);????????????????????????????????? %畫已走的路徑連線。
?? set(H_line2,'color','red','linewidth',2);???? %設置顏色和線寬。
?????? xt=xi-dz1;yt=yi-dz2;
?????? H_line=plot([xi xt],[yi yt],'k:','linewidth',1);??? %畫最速下降方向路徑。
?? end?????????? %若按左鍵button=1,繼續循環。若按右鍵,button~=1,循環終止 。 】
zxy6_3f.m(模擬山谷的二次函數程序)
【???? function [f,df1,df2]=zxy6_4f(x1,x2)
?f=8*x1.*x1+9*x2.*x2-10*x1.*x2-12*x1-6*x2;?????? %計算函數值。
?if nargout > 1
?? df1=2*8*x1-10*x2-12*ones(size(x1));??????????????? %計算梯度向量。
?? df2=2*9*x2-10*x1-6*ones(size(x2));
end?? ????????????】
6.3 .實驗與觀察(Ⅱ):Matlab優化工具箱簡介
6.3.1多元函數無約束優化指令fminunc和fminsearch
1. 觀察:運行香蕉函數的優化程序bandemo.m
????
2. 使用fminunc和fminsearch指令
????
??????? ◆ 觀察:用inline生成函數。
【????? f=inline('100*(x(2)-x(1)^2)^2+(1-x(1))^2'),
??? x=[2,2],y=f(x),??? %代入一個點計算看看效果 。???????????? 】
3. bandemo.m的簡化和剖析
zxy6_4.m
【 clf;? clear???????????????????
?????? %以下程序段是畫香蕉函數圖形。
xx = [-2:0.125:2]'; yy = [-1:0.125:3]'; [x,y]=meshgrid(xx',yy') ;
meshd = 100.*(y-x.*x).^2 + (1-x).^2; conts = exp(3:20);
xlabel('x1'),ylabel('x2'),title('Minimization of the Banana function')
contour(xx,yy,meshd,conts), hold on
plot(-1.9,2,'ro'),text(-1.9,2,'Start Point')
plot(1,1,'ro'),text(1,1,'Solution')
%優化程序段開始。
x0=[-1.9,2];??????? %賦初值。
l=1;
while l?????????? %while 語句是可以重復運行下面的程序段,直至l=0退出循環。
???????? clc???????????????? %清除命令窗口的全體內容 。
%以下程序段是在命令窗口顯示相應的文字內容 。?
??????? disp(' ')
??????? disp('?? Choose any of the following methods to minimize the …?
?????????????????? banana?? function')
??????? disp('')???????
??????? disp('??? UNCONSTRAINED:??? 1) BFG direction ')
??????? disp('???????????????????????????????????? 2) DFP direction')
??????? disp('???????????????????????????????????? 3) Steepest Descent direction')
??????? disp('???????????????????????????????????? 4) Simplex Search')
??????? disp('???????????????????????????????????? 0) Quit')
??????????????????? method=input('Select method : ');? % input 從鍵盤輸入控制變量method數據。
? switch method???????? %Switch體開始。
???? case 0???????????? %當method=0,終止程序。
??????? hold off
??????? disp('End of demo')
??????? break???????????????????????? %break指令:中止程序。
???? case 1????????????? %當method=1,采用BFGS法。
??????? clf,hold on??? %每一個case中重新畫等值線圖,下面的程序段是重新畫圖。
??????? xlabel('x1'),ylabel('x2'),
??????? title('Minimization of the??? Banana function')
??????? contour(xx,yy,meshd,conts)
??????? plot(-1.9,2,'ro'), text(-1.9,2,'Start Point')
??????? plot(1,1,'ro'), text(1,1,'Solution')
????????????? % 這里是學習的重點: OPTIONS是控制fminunc和fminsearch指令的重要參數,
?????? %用optimset('屬性','屬性值',…)指令改變設置,可以容易地控制算法。
??????????? OPTIONS=optimset('LargeScale','off');?
???????????? %fminunc默認的大規模算法是“信賴域方法”,這是一種有效的算法;
?????? %將LargeScale的屬性設置為off時,fminunc的默認中等規模的算法就是BFGS方法。??????
??????????? OPTIONS = optimset(OPTIONS,'gradobj','on'); %使用解析梯度。
????????? %定義梯度函數和畫圖函數banplot6_4。
GRAD=inline('[100*(4*x(1)^3-4*x(1)*x(2))+2*x(1)-2;…
???????????????????? 100*(2*x(2)-2*x(1)^2); banplot6_4(x)]');??
f=inline('100*(x(2)-x(1)^2)^2+(1-x(1))^2'); %定義目標函數。
?????????? disp('[x,fval,exitflag,output] = fminunc({f,GRAD},x0,OPTIONS);');
????????????? %(調用fminunc指令,輸出x,fval分別為最優點和最優函數值,exitflag和output
????? % 提供算法的一些信息,讀者可在程序結束后,鍵入output或exitflag查看這些信息)
????????????? [x,fval,exitflag,output] = fminunc({f,GRAD},x0,OPTIONS);
??????? hold off
??????? disp(' ')
??????? disp('Strike any key for menu')
??????? pause
??????????? case 2????? %當method=2,采用DFP法。
?????? clf,? xlabel('x1'),ylabel('x2'),
?????? title('Minimization of the Banana function')
?????? contour(xx,yy,meshd,conts),? hold on
??????? plot(-1.9,2,'ro'),?? text(-1.9,2,'Start Point')
??????? plot(1,1,'ro'),???? text(1,1,'Solution')
?????? OPTIONS=optimset('LargeScale','off');
?????? OPTIONS = optimset(OPTIONS,'gradobj','on');
??????? OPTIONS=optimset(OPTIONS,'HessUpdate','dfp');?????
???????????????? % 將HessUpdate屬性設置為dfp就使fminunc指令采用DFP法。
??????? GRAD=inline('[100*(4*x(1)^3-4*x(1)*x(2))+2*x(1)-2;…
?????????????????????????????? 100*(2*x(2)-2*x(1)^2); banplot6_4(x)]');
??????? f=inline('100*(x(2)-x(1)^2)^2+(1-x(1))^2');
??????? disp('[x,fval,exitflag,output] = fminunc({f,GRAD},x0,OPTIONS);');
??????? [x,fval,exitflag,output] = fminunc({f,GRAD},x0,OPTIONS);
??????? hold off
??????? disp(' ')
??????? disp('Strike any key for menu')
??????? pause
???? case 3?? %當method=3,采用最速下降法。
????? clf,?? xlabel('x1'),ylabel('x2'),
????? title('Minimization of the Banana function')
??????? contour(xx,yy,meshd,conts)
??????? hold on
??????? plot(-1.9,2,'ro'),? text(-1.9,2,'Start Point')
??????? plot(1,1,'ro'),???? text(1,1,'Solution')
?????? OPTIONS=optimset('LargeScale','off');
?????? OPTIONS = optimset(OPTIONS,'gradobj','on');
?????? OPTIONS=optimset(OPTIONS,'HessUpdate','steepdesc');
????????????? %將HessUpdate屬性設置為steepdesc就使fminunc指令采用最速下降法。
?????? GRAD=inline('[100*(4*x(1)^3-4*x(1)*x(2))+2*x(1)-2;…
??????????????????????????? 100*(2*x(2)-2*x(1)^2); banplot6_4(x)]');
?????? f=inline('100*(x(2)-x(1)^2)^2+(1-x(1))^2');
?????? disp('[x,fval,exitflag,output] = fminunc({f,GRAD},x0,OPTIONS);');
?????? [x,fval,exitflag,output] = fminunc({f,GRAD},x0,OPTIONS);
??????? hold off
??????? disp(' ')
??????? disp('Strike any key for menu')
??????? pause
??? case 4????????? %當method=4,采用單純形方法。
??????? clf,hold on,? xlabel('x1'),ylabel('x2'),
??????? title('Minimization of the Banana function')
??????? contour(xx,yy,meshd,conts),
??????? plot(-1.9,2,'ro'),? text(-1.9,2,'Start Point')
??????? plot(1,1,'ro'),????? text(1,1,'Solution')
?????? OPTIONS=optimset('LargeScale','off');
??????? OPTIONS = optimset(OPTIONS,'gradobj','off');
???????????? %該方法不使用導數,所以要設置gradobj屬性為off。
?????? f=inline('[100*(x(2)-x(1)^2)^2+(1-x(1))^2; banplot6_4(x)]');
???????????? %如果要畫迭代過程的中間圖,就要編制一個畫圖程序 banplot6_4,
???????????? % 套用本程序的格式定義目標函數。
?????? disp('[x,fval,exitflag,output] = fminsearch(f,x0,OPTIONS);');
?????? [x,fval,exitflag,output] = fminsearch(f,x0,OPTIONS);
?????????????? %fminsearch 是多變量函數尋優的單純形法指令,用法和fminunc是類似的。???????
??????? hold off
??????? disp(' ')
??????? disp('Strike any key for menu')
??????? pause
??? end
?end?????????????????????????????????????? 】
?banplot6_4.m
【function out =? banplot6_4(x)
plot(x(1),x(2),'O','Erasemode','none')
drawnow;???????? % Draws current graph now
out = [];????????????????????????????? 】
?6.3.2其它的優化算法指令
1.多變量約束優化指令fmincon
2. 線性規劃linprog指令
【??? f = [-5; -4; -6]; A =? [1 -1? 1;3? 2? 4;3 2 0];b = [20; 42; 30];
lb = zeros(3,1); x0=[1,1,0];
options=optimset('Diagnostics','on', 'largescale','off');???
???????? %查看診斷信息并采用單純形算法
[x,fval,exitflag,output,lambda]= …linprog(f,A,b,[],[],lb,[],x0,options)
???????? %沒有等式約束且變量無上界,故需置Aeq=[ ];Aeb=[ ];ub=[ ];?????????????? 】
3. 二次規劃quadprog指令
4. 一元函數尋優fminbnd指令
5.非線性最小二乘指令lsqnonlin和非線性數據擬合指令lsqcurvefit??
程序如下(zxy6_5.m)
【??? clf;x=1:10; y=2+2*x;??????????????????????????????????? %選直線上的10個點。
a0=[0.1,0.4]; y1=exp(x*a0(1))+exp(x*a0(2));? %計算一條曲線。
[a,resnorm,residual] = lsqnonlin('zxy6_5f',a0); % 求最優解初始點a0。
disp('a='), disp(a);
disp('resnorm='), disp(resnorm)
y2=exp(x*a(1))+exp(x*a(1));
plot( -x,y,x,y1,'r:',x,y2,'o-',x,residual,'.-'),grid on
legend('直線','猜測的曲線','解曲線','殘差')???????????????????????? 】
函數子程序為(zxy6_5f.m)
【??? function F = zxy6_5f(a)
x = 1:10;
F = 2 + 2*x-exp(a(1)*x)-exp(a(2)*x);??????????????????? 】
{???? Optimization terminated successfully:
Norm of the current step is less than OPTIONS.TolX
a=??? 0.2578??? 0.2578
6.4 應用、思考與練習
6.4.1 .計算最佳水槽斷面面積
zxy6_6S.m
【????? function s=zxy6_6S(x)
?? l=24;a(1)=x(3);a(2)=x(4);?? xs0=(0.5*l-x(1)-x(2));
?? xs1=xs0+x(1)*cos(a(1));???? xs2=xs1+x(2)*cos(a(2));
?? h1=x(1)*cos(a(1));???????????? h2=x(2)*cos(a(2));
?? s=(xs0+xs1)*h1+(xs1+xs2)*h2;s=-s;??????????????????? 】
zxy6_6.m
【??? clf,A=[1,1,0,0;-1,-1,0.0,0.0];b=[12,0]';
?????? lb=[0,0,0,0]';ub=[100,100,pi/2,pi/2]';x0=[4,4,pi/3,pi/3]';
????? [s,fval] = fmincon('zxy6_6S',x0,A,b,[],[],lb,ub)?????? %最優化計算
???????? %以下是繪制最優斷面的圖形,首先計算坐標點。將底邊放在x軸上,并讓斷面關于
?%y軸對稱。逆時針計算坐標點,使之成為一個封閉的圖形)
????? x(1)=(24-2*s(1)-2*s(2))/2; y(1)=0;
x(2)=x(1)+s(1)*cos(s(3));? y(2)=s(1)*sin(s(3));
x(3)=x(2)+s(2)*cos(s(4));? y(3)=y(2)+s(2)*sin(s(4));
x(4)=-x(3); y(4)=y(3);x(5)=-x(2); y(5)=y(2);x(6)=-x(1); y(6)=y(1);
x(7)=x(1);y(7)=y(1);??????? %首尾相接。
%plot(x,y),axis equal?????? %用這命令可畫出封閉圖形。
patch(x,y,'y'); axis equal,? %用patch命令畫塊對象并填充顏色。???? 】
{????? s =??? 4.8000??? 4.8000??? 0.6283??? 1.2566
?fval =? -88.6373??????????????????????????????????????????? }
6.4.2? 對約束優化的討論
6.4.3.工程優化問題的計算
1. 啤酒配方問題: 線性規劃
2.? 儲能飛輪的設計
3.? 齒輪減速器設計
 電子發燒友App
電子發燒友App























評論