matlab概率統計實驗
9.1 實驗（I）：Galton釘板試驗
9.1.1 實驗與觀察: Galton釘板模型和二項分布
       
1. 動畫模擬Calton釘板試驗
【    rand('seed',1), u=rand(1,6)  】
【    rand('seed',2),u=rand(1,6)  】
   觀察程序zxy9_1.m
【   clear，clf,     m=100;n=5;y0=2;      %設置參數。
ballnum=zeros(1,n+1);
p=0.5;q=1-p;
for i=n+1:-1:1             %創建釘子的坐標x,y 。 
   x(i,1)=0.5*(n-i+1);y(i,1)=(n-i+1)+y0;
   for j=2:i
      x(i,j)=x(i,1)+(j-1)*1;y(i,j)=y(i,1);
  end
end
mm=moviein(m);        % 動畫開始，模擬小球下落路徑。
for i=1:m
   s=rand(1,n);            %產生n個隨機數。
   xi=x(1,1);yi=y(1,1);k=1;l=1;    % 小球遇到第一個釘子。
   for j=1:n
       plot(x(1:n,:),y(1:n,:),'o',x(n+1,:),y(n+1,:),'.-'), % 畫釘子的位置 。
       axis([-2 n+2 0 y0+n+1]),hold on            
       k=k+1;                               % 小球下落一格 。  
      if s(j)>p 
         l=l+0;                                %小球左移 。       
      else
         l=l+1;                                %小球右移 。    
      end
      xt=x(k,l);yt=y(k,l);              %小球下落點的坐標。
      h=plot([xi,xt],[yi,yt]);axis([-2 n+2 0 y0+n+1])      %畫小球運動軌跡。
      xi=xt;yi=yt;                         
   end
      ballnum(l)=ballnum(l)+1;                    %計數。
      ballnum1=3*ballnum./m;
      bar([0:n],ballnum1),axis([-2 n+2 0 y0+n+1])  %畫各格子的頻率 。
     mm(i)=getframe;                  %存儲動畫數據。
hold off
end 
movie(mm,1)                    %播放動畫1次。     】

2. 用二項分布描述Galton釘板模型
【      X = binornd(5,0.5,1,10)       】
3.  數學期望和平均收益
【  n=5;p=0.5; m=5000;
rand('seed',5); R = binornd(n,p,1,m);   %模擬投球。
f=[5, 1, 0.2, 0.2, 1, 5];                        %獎品的價值向量。
s=[];                         
for k=1:n+1                                         %計算第0～n格獎品價值。
u=[];
   u=find(R==(k-1));                  %計算落入第k-1格的小球下標，并存于向量u中。
   s=[f(k)*length(u),s];               %計算相應的獎品價值，并存于向量s中。  
end
   mean_return=sum(s)/m           %計算一次抽獎的平均回報 。   】
{     mean_return =  0.7506               }
【    f=[5, 1, 0.2, 0.2, 1, 5]; x=[0:1:n]; pu=binopdf(x,n,p);EF=sum(f.*pu)   】
9.1.2 應用、思考和練習
1. 二項分布的應用模型
         ◆電力供應問題 。
         提示：
【       x=linspace(90,160,10);  r = binornd(200,0.6,1,960);  hist(r,x)  ;
           [n,x]=hist(r,x);             】
        ◆ 廢品問題。
      
 下面的程序可作為參考 。
【   clear,clf ,n=50;r=linspace(0,1,n);s=linspace(0,10,n);
[R,S]=meshgrid(r,s); x=[0 1 2 3 4 5];p = binopdf(x,5,0.5);
for k=1:n
  f=[S(k,l) S(k,l)*R(k,l) S(k,l)*R(k,l)^2  S(k,l)*R(k,l)^2 S(k,l)*R(k,l) S(k,l)];
  for l=1:n
     z(k,l)=sum(f.*p);
       if z(k,l)>=1  z(k,l)=NaN;  end
  end
end
contour(R,S,z)              】
3. 單服務臺定長服務時間排隊系統的計算機模擬
      
4.  隨機變量的模擬：逆概率法 
       
 
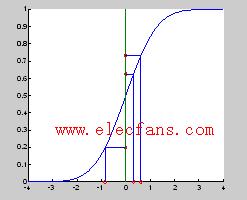
圖9.4    逆概率法模擬隨機數原理。
【   clf
mu=0;sigma=1;a=mu-4*sigma;b=mu+4*sigma;
t=linspace(a,b,30);
f1=normcdf(t,mu,sigma);
for i=1:3
   hold on
   u=rand(1);
   f=norminv(u,mu,sigma);
   plot(t,f1,[0 0],[0,b]),hold on,
   plot(0,u,'rO'),plot([0,f],[u,u]);plot([f,f],[u,0]);
   plot(f,0,'rO'),   axis([-4 4 0 1])
end     】
9.2  實驗(Ⅱ) ：熱軋機的調整
9.2.1實驗與觀察: 控制粗軋的浪費
         
1. 用正態分布描述熱軋機模型
       
2.  調整額定長度使浪費最小
        .觀察程序
        
zxy9_2.m
【    clf,clear,  m=20;l=3;mu=3.5;sigma=0.3; mu1=3.5;sigma1=0.9;
        a=0; b=max([mu+4*sigma,mu1+4*sigma1]);     %設定坐標的范圍。
        subplot(2,2,1),
for k=1:m
    rand('seed',1), x=normrnd(mu,sigma);
    plot([0,x],[k,k],'linewidth',5),hold on, axis([0 mu+4*0.6 -2 m+5])
end
plot([l,l],[-2,m+5],'r-');hold on,axis([a b -2 m+5])
       subplot(2,2,3),
t=linspace(a,b,50);f=normpdf(t,mu,sigma);
y0=max(f)+0.1;plot(t,f),hold on,axis([a b 0 y0]),
plot([l,l],[0,y0],'r-',[mu,mu],[0,y0],'r:');hold on
t=linspace(a,b,30);f=normpdf(t,mu,sigma);plot(t,f)
       subplot(2,2,2)
for k=1:m
   rand('seed',1),x=normrnd(mu1,sigma1);
   plot([0,x],[k,k],'linewidth',5),hold on,axis([a b -2 m+5])
end
plot([l,l],[-2,m+5],'r-');hold on
       subplot(2,2,4),
t=linspace(a,b,50);f=normpdf(t,mu1,sigma1);y0=max(f)+0.1;
plot(t,f),hold on,axis([a b 0 y0])
plot([l,l],[0,y0],'r-',[mu1,mu1],[0,y0],'r:');hold on               】

        下面是觀察與實驗程序zxy9_3.m，對照上一節給出的算法，這一程序也是不難理解的。 
 zxy9_3.m
 【   clf,clear
l=2;sigma=0.2;
n=10000;m=50;a=2.2;b=3;
mu=linspace(a,b,m);
for k=1:m
 x=normrnd(mu(k),sigma,1,n);  %模擬軋鋼。
 k_chenpin=find(x>=l);             %求可軋制的成品材的下標。
 k_feipin=find(x<l);                 %求整根報廢鋼材的下標。
 w_chenpin=x(k_chenpin)-l;     %計算浪費量。
 w_feipin=x(k_feipin);             %計算浪費量。
 if length(k_chenpin)==0
   waste(k)=NaN;
 else
   waste(k)=(sum(w_chenpin)+sum(w_feipin))/length(k_chenpin);  
 end
end
[wmin,i]=min(waste);       %求最小浪費量及其下標。
[mu(i) wmin]
plot(mu,waste,'.-',mu(i),wmin,'ro'),set(gca,'fontsize',15)
text(mu(i),wmin,['\bullet\leftarrow The Min Value is ',num2str(wmin),' at \it{mu}= ',num2str(mu(i))]);  】
9.2.2應用、思考與練習
1. 隨機優化：確定熱軋機的額定長度  
2. 二維正態分布: 如何制定胖和瘦的標準？
      題的思路，這種思路在實踐中經常被采用，真正要確定正常體重標準可能要復雜得多。          
          ◆。
      【    clear,clf
n=1000;x=normrnd(170,4.5,1,n);
y=0.36*x+normrnd(0,7,1,n);
a=min(x);b=max(x);c=min(y);d=max(y);xx=linspace(a,b,20);
yy=0.36*xx;plot(x,y,'ko'),hold on,
plot(xx,yy,'k-','linewidth',5),grid,
axis([a b c d]),axis('equal'),
xlabel('身高X');ylabel('體重Y');  】
         ◆ （2）觀察    
       程序zxy9_4.m （畫圖9.8）
【   clear,clf,n=1000;m=15;x=normrnd(170,4.5,1,n);
y=0.36*x+normrnd(0,7,1,n);a=min(x);b=max(x);c=min(y);d=max(y);
h1=(b-a)/m;h2=(d-c)/m;
xx=linspace(a-h1,b+h1,m);yy=linspace(c-h2,d+h2,m);
[X,Y]=meshgrid(xx,yy);
for k=1:m             %計算頻數。
 for l=1:m
     j=find(x>=(X(k,l)-h1)&x<=(X(k,l)+h1));
     h=find(y(j)>=(Y(k,l)-h2)&y(j)<=(Y(k,l)+h2));
   z(k,l)=length(h)/n;
end
end 
mu=[170 0.36*170];              %計算二維正態分布密度。
C=[4.5^2 0.36*4.5^2; 0.36*4.5^2, (0.36*4.5)^2+7^2];
detC=det(C);
for k=1:m
 for l=1:m
   u=[X(k,l),Y(k,l)]'-mu';s=2*pi*sqrt(detC);
   z1(k,l)=s^-1*exp((-0.5)*u'*C^-1*u);
end
end 
subplot(2,2,1),surf(X,Y,z),axis([a b c d 0 0.15]),
set(gca,'fontsize',15);
subplot(2,2,2),contour(X,Y,z),axis([a b c d ]),axis('equal'),
subplot(2,2,3),surf(X,Y,z1),axis([a b c d 0 0.005]),
subplot(2,2,4),contour(X,Y,z1),axis([a b c d ]),axis('equal')】
3.用線性回歸方法確定正常體重標準
         觀察：
    ◆（1）參考程序 zxy9_4.m中的模擬部分，。
     
【   alpha=0.01; polytool(x',y',1,alpha)    】
               ◆（3) 用 多元線性回歸指令regress做體重預測。
     
       ◆對模擬的100對身高體重數據，運行下面的程序，了解指令regress 的用法。
【  [b,bint,r,rint,stats] = regress(y',[ones(100,1) x']);
b,bint,stats
rcoplot(r,rint),set(gca,'fontsize',15)  】
9.3實驗（Ⅲ）參數估計和假設檢驗
9.3.1實驗與觀察: 極大似然估計
1.極大似然估計原理: 如何決定廢品率？
         觀察
         ◆（1）
  【       clear,p=0.04; n=10;     %設定產品的檔次，抽樣次數。
         for k=1:n               %抽樣n次。
            r(k)=rand(1,1);   %產生隨機數。
            if r(k)<=p
               x(k)=1;           %抽樣得到廢品。   
             elseif r(k)>p
              x(k)=0;            %抽樣得到正品 。  
            end
         end
I=[1:n];[I;x]  】
        ◆ （2）
2.實驗觀察的參考程序    
    實驗觀察的主要程序為zxy9_5.m，其源代碼如下，該程序是不難讀懂的。
zxy9_5.m
【   clear,clf,n=50;
p=0.04;
rand('seed',1),r=rand(1,n);
k=+find(r<=p);
x=zeros(1,n);
x(k)=ones(1,length(k));
p_estimate=sum(x)/n,
t=[0.01 0.02 0.03 0.04 0.05 0.06];
%t=linspace(0.01,0.5,40)
Lt=t.^sum(x).*(1-t).^(n-sum(x));
%lnLt=sum(x)*log(t)+(n-sum(x))*log(1-t);
set(gca,'fontsize',16),
plot(t,Lt,''),
[Lmax,I]=max(Lt);
tmax=t(I);
text(t(I),Lmax,['\fontsize{16}\leftarrow\it Lmax=' ,num2str(Lmax)])
text(t(I),0.95*Lmax,['\fontsize{16}\it{ at  p}= ',num2str(tmax)])
xlabel('p','fontsize',16);ylabel('L(p)','fontsize',16);  】
  9.3.2 應用、思考與練習 
1. 用Matlab符號演算求解極大似然估計
          ◆ 練習：用Matlab符號演算指令求解9.3.1節中廢品問題的似然方程獲得極大似然估計。
      【     syms p                %未知參數為p,所以作為符號變量處理，用syms指令說明。
clear,clf,n=50;               %產生50個樣本。
p=0.04;                          %設定真實參數。
x=zeros(1,n);                  %令x全為0   。
rand('seed',1),r=rand(1,n);
k=+find(r<=p);               %找出廢品的下標。  
x(k)=ones(1,length(k));   %在廢品下標處改x為1；x為50個樣本觀察值。
%觀察似然函數和似然方程的一般表達式。
L=sym('p^sx*(1-p)^(n-sx)')     %正確寫出似然函數，L是符號p的函數。   
likely_equ=diff(L,'p')               %對p進行符號求導，得到似然方程。 
%觀察含具體數值的似然函數和似然方程               
sx=sum(x), p='p';           %代入sx的具體數值。    
Lp=subs(L)                    %將具體的數值代入似然函數中 。
likely_equ=diff(Lp,'p')    %求似然方程 。          】
         【   %求似然方程的符號解，得到極大似然估計
 s=solve('p^sx*sx/p*(1-p)^(n-sx)-p^sx*(1-p)^(n-sx)*(n-sx)/(1-p)=0','p')
 sx,n            %看看具體的數值。
 sp=subs(s)  %對已獲得的樣本，觀察極大似然估計的具體數值。              】 
2. 水庫入庫徑流的分布估計
      
7月上旬徑流數據
  356         258         222         208         163         342         501         501         782         225         630        2305           
   931         485        503         501          422         101        280       1807         922         390         466          211       
   922        444         233         370          788          802        219         524         470       1097       1160         702         
   566        222         630
7月中旬徑流數據
   98        262         117        1687         291        1318         292         716         254          519         270         273         
 275         274         374        147          345          70          940         440        2839         141         699         324         
 900         311         870        596          187      2231          111         949          303         888         328         459         
 370       1360       1320
7月下旬徑流數據
    69       133         392         596        4518        1051         336         867          541        1733          149       266       
  324     1365         891         918        1751         219          513         438        1033        1217        1290       247        2360     1023         453       1622         1272      1383        1217      1530         1724          703          299      638        
   548    1200       1220 
 zxy9_6.m
【     clear,clf,
Q=[ 98      262         117        1687         291        1318         292         716         254        519         270         273         275         274         374        147          345          70          940         440        2839         141         699         324         900         311         870         596         187        2231         111         949         303         888         328         459         370        1360      1320];
     m=50;
     as=linspace(0.6561, 2.2477,m);
     bs=linspace(215.4687, 637.4421,m);
     [A B]=meshgrid(as,bs);
     for i=1:m
        for j=1:m
           ax=A(i,j);bx=B(i,j);
           y(i,j) = sum(log(gampdf(Q,ax,bx)));
        end
     end 
     [y0,s]=max(y);     [y00,s0]=max(y0);
     a_est=A(s0,s(s0));b_est=B(s0,s(s0));     meshc(A,B,y),hold on
     plot3(a_est,b_est,y00,'.','markersize',25);
     text(a_est,b_est,y00+0.06*abs(y00),['(a_e_s_t,b_e_s_t,L_m_a_x)=']);
     text(a_est,b_est,y00+0.03*abs(y00),['(',num2str(a_est),',',num2str(b_est),',',num2str(y00),')'])
     figure(2)
     [h,n0]=hist(Q,5);     h0=max(h);     a=min(Q)-100;b=max(Q);
     x=linspace(a,b,30);     hist(Q,5);     hold on
     y = gampdf(x,a_est,b_est);
     plot(x,h0*y/max(y),'r-','linewidth',5);       】

3. 數學建模競賽: 零件的參數設計
 
zxy9_7.m
【    clear,clf, n=1000; A=0.01/3;B=0.05/3;C=0.1/3;
%x=[0.075,0.375,0.125,0.1198,1.252,12.5,0.77];%A=[B B B C C B B];
x=[0.1 0.3 0.1 0.1 1.5 16 0.75];   %設置標定值。
A=[B C C C C C B];                    %設置容差。    
X1=normrnd(x(1),A(1)*x(1),n,1);  %模擬零件參數。
X2=normrnd(x(2),A(2)*x(2),n,1);X3=normrnd(x(3),A(3)*x(3),n,1);
X4=normrnd(x(4),A(4)*x(4),n,1);X5=normrnd(x(5),A(5)*x(5),n,1);
X6=normrnd(x(6),A(6)*x(6),n,1);X7=normrnd(x(7),A(7)*x(7),n,1);
Y=z9_5fun(X1,X2,X3,X4,X5,X6,X7);    %模擬y的樣本。
k=find(imag(Y)==0);Y1=Y(k);          %如果產生了復數，剔除復數。
histfit(Y1)                                        %直方圖和正態密度擬合。
dh=0.001;                                         %求數值導數。
for i=1:7
   for j=1:7
      xx(:,j)=x(j)*ones(2,1);
   end
   xx(:,i)=linspace(x(i),x(i)+dh,2)';
   F(:,i)=z9_5fun(xx(:,1),xx(:,2),xx(:,3),xx(:,4),xx(:,5),xx(:,6),xx(:,7));
   g(:,i)=diff(F(:,i),1)/dh;                 %求數值導數。
end
mu=F(1,1),EY=mean(Y1),         %均值對比。
R=(A.*x).^2;
sigma=sqrt(sum((g.^2).*R)),DY=std(Y1), %均方差值對比.
[h,p,ci]=ttest(Y1,mu,0.01,0)                    %均值的t－檢驗 。   】
zxy9_6fun.m（計算函數的子程序）
【      function y=zxy9_5fun(x1,x2,x3,x4,x5,x6,x7)
   y1=174.42*(x1./x5).*(x3./(x2-x1)).^0.85;
   y2=(1-0.36*(x4./x2).^(-0.56)).^(1.5) ;
   y3=(1-2.62*y2.*(x4./x2).^1.16)./(x6.*x7);
   y=y1.*sqrt(y3);        

200多個MATLAB經典教程和MATLAB論文請查看：matlab教程