了解信號的對稱性如何可以簡化計算傅里葉系數時,用來找到電路的穩態響應
求一個波形的傅里葉級數系數往往涉及一些相對繁瑣的計算。只有通過目視檢查波形,不執行一個單一的計算,有時是可能的,以確定哪些系數將工作到零。當波形具有某種類型的對稱性時,就可以做到這一點。請繼續閱讀,了解這些對稱性,以及如何使用它們來簡化傅里葉系數的計算。
理解傅里葉級數系數
下面的方程可以用來表示一個周期信號 f (t) ,周期 T 用它的傅里葉級數系數表示:
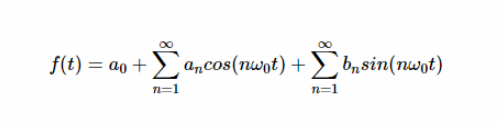
?
其中 a0,an 和 bn 是信號的傅里葉系數 ω
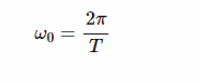
?
表示周期信號的基頻。頻率 nω0被稱為波形的 n 次諧波。
這些系數可用下列公式計算:

?
等式1
?
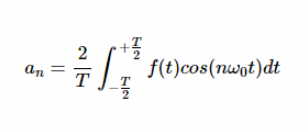
?
方程式2
?
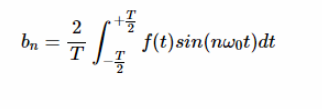
?
方程式3
?
讓我們看看不同類型的對稱是如何簡化上述系數的計算的。
偶函數對稱性
圖1顯示了一個周期 T 波形的例子,它甚至具有對稱性。
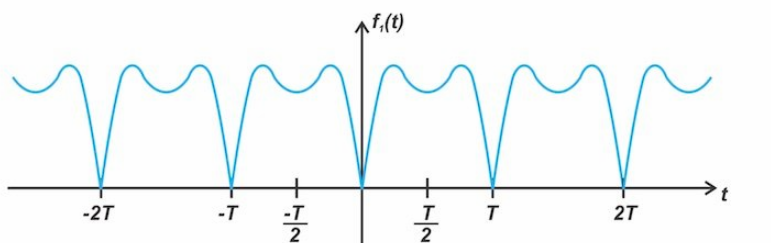
圖1。一個周期為 T 的對稱波形的例子
?
偶函數的圖形是關于垂直軸(y 軸)對稱的。在數學語言中,f (t)是即使它滿足以下條件:
F (- t) = f (t)
?
偶數函數的一個熟悉的例子是 f (t) = cos (t) ,因為它為給定 t 的正值和負值產生相同的值。圖2繪制了 f2(t) = cos (2πt)。
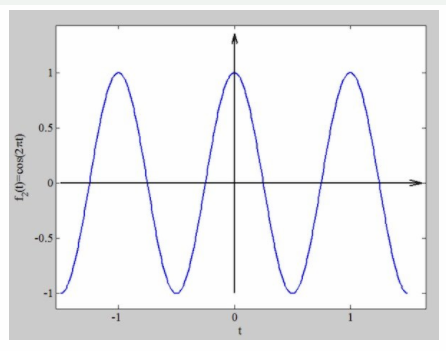
圖2. f2(t) = cos (2πt)的函數圖示例
?
另一個偶數信號如圖3所示。
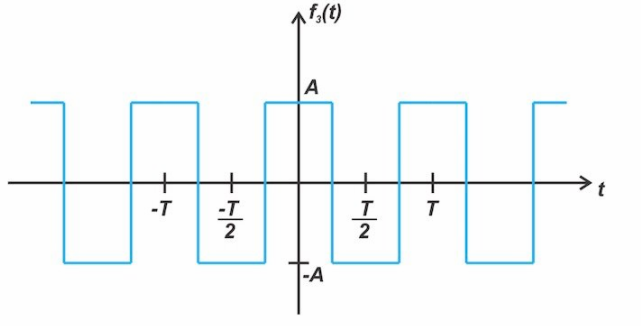
圖3。偶數信號的一個例子
?
雖然圖1和圖3中的 f1(t)和 f3(t)具有偶對稱性,但我們將很快討論 f3(t)具有其他對稱性水平,即半波對稱性和四分之一波對稱性。現在,只需要注意 f3(t)在其周期的后半部分,比如 T/2到 T 間隔,等于信號在前半周期(0到 T/2間隔)中的負值。
奇函數對稱性
具有奇對稱性的函數示例如圖4所示。
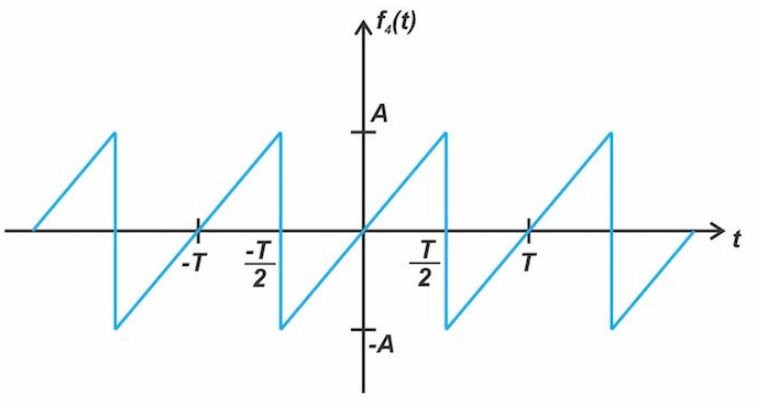
圖4。一個奇對稱的函數示例
?
奇函數的圖是關于原點的對稱圖。如果 f (t)是一個奇函數,它滿足以下條件:
F (- t) =-f (t)
?
與余弦不同,正弦函數是一個奇數函數。圖5顯示了 f (t) = sin (2πt)的曲線。
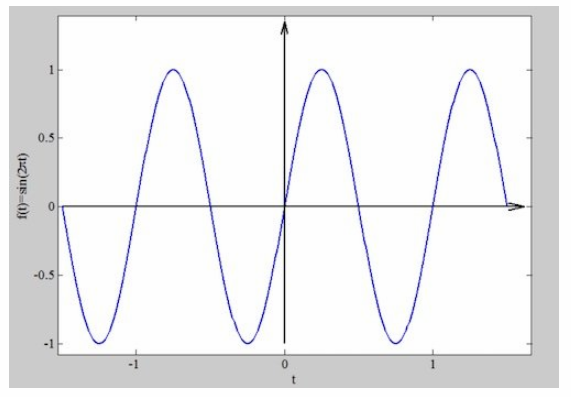
圖5. f (t) = sin (2πt)的示例圖形圖函數
?
另一個示例如圖6所示。
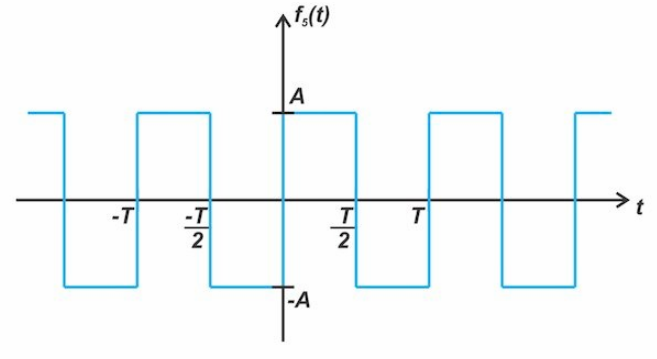
圖6. 同一繪圖的另一個圖形示例
?
圖4和圖6所示的 f4(t)和 f5(t)都具有奇對稱性,而 f5(t)也具有半波對稱性和四分之一波對稱性。請注意,f5(t)在其周期的后半段產生的值,比如 T/2到 T 間隔,等于信號在前半個周期(0到 T/2間隔)中獲得的值的負值。
在討論這些對稱性對傅里葉系數的影響之前,讓我們先看看計算信號的積分是如何受到偶對稱性和奇對稱性的影響的。
奇偶信號的積分
考慮在從-a 到 + a 的對稱區間上積分偶數函數 f (t)。我們可以把這個積分寫成從-a 到0和0到 + a 的兩個積分之和,如下所示:
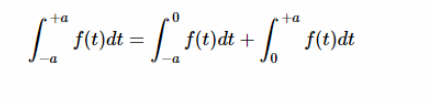
?
方程式4
?
之前,我們看到偶數函數是對稱于 y 軸的。由于這種對稱性,f (t)在-a 到0的區間下的面積與0到 + a 的區間下的面積相同。
因此,上述積分可重寫為:
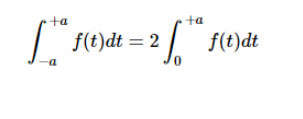
?
等式5
?
另一方面,如果我們假設 f (t)具有奇對稱性,那么方程4中的積分就是零,因為-a 到0的區間的面積是0到 + a 區間的面積的負數。這意味著假設奇對稱,我們得到:
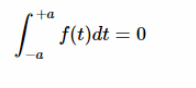
?
偶對稱性對傅里葉級數的影響
如果 f (t)具有偶對稱性,我們可以將方程1簡化如下:
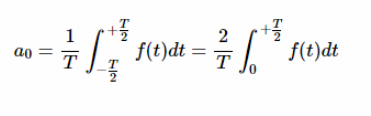
?
此外,如果 f (t)是偶數,可以很容易地驗證 f (t) cos (nω0t)和 f (t) sin (nω0t)分別具有偶對稱和奇對稱。所以,
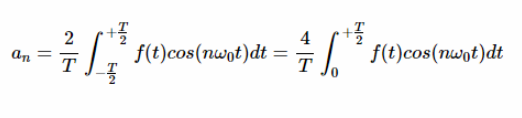
?
還有,
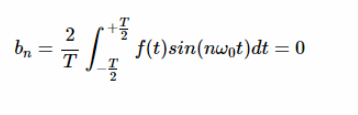
?
因此,對于偶數信號,所有的 bn 系數都為零。
奇對稱性對傅里葉級數的影響
如果 f (t)具有奇對稱性,則 f (t) cos (nω0t)和 f (t) sin (nω0t)分別具有奇對稱性和偶對稱性。
因此,方程式1至3簡化為:
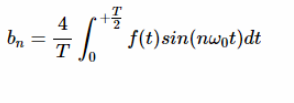
?
因此,對于奇數信號,所有的系數都為零。
半波對稱性
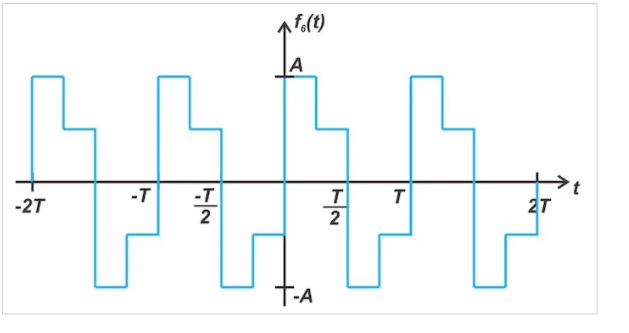
在具有半波對稱性的信號中,每個周期可分為兩個半周期,其中兩個半周期的形狀完全相同,但相互顛倒。換句話說,第二個半周期與第一個半周期相同,是圍繞水平軸(時間軸)倒轉的。具有半波對稱性的波形示例如圖7所示。
?
圖7。一個半波對稱波形的例子
?
在數學語言中,這一特征可以用以下條件來描述:
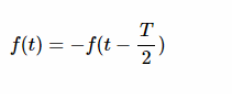
?
方程式6
?
這意味著如果我們將信號沿著時間軸移動 T/2并反轉,我們將獲得原始信號。
考慮到這一點,半波對稱性將如何影響信號的傅里葉系數?
具有半波對稱性的信號由相同的半周期和相反的極性組成。由于這種交替特征,我們可以得出結論,信號的平均值為零。所以半波對稱消除了 a0系數,因為這個系數對應于信號的平均值。然而,計算其他系數有點復雜。
對于 a,我們從方程2開始,把積分分成兩個區間:
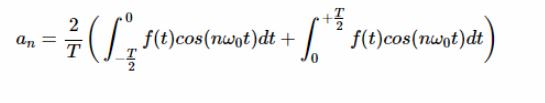
?
方程式7
?
現在,我們嘗試用第二個積分來重寫第一個積分,這樣就可以考慮 f (t)的半波對稱性。
我們可以定義一個新變量如下:
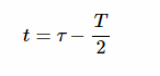
?
對于 t =-T/2和 t = 0,新的變量分別是 τ = 0和 τ = T/2。還注意到 dt = dτ,第一個積分可以重寫為:
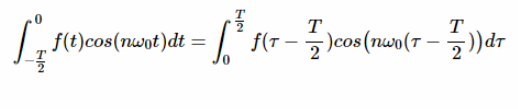
?
等式8
?
余弦項可簡化如下:
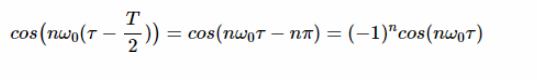
?
方程式9
?
應用半波對稱性(方程6)和取代方程9,我們可以把方程8表示為:
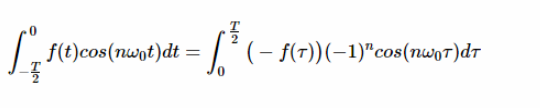
?
方程式10
?
對于奇數 n,上面的積分等于方程7中的第二個積分。然而,對于偶數 n,上面的積分等于該積分的負數。因此,對于具有半波對稱性的信號,對于 n 的偶數值,系數為零。對于 n 的奇數值,我們有:
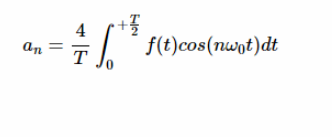
?
等式11
?
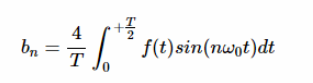
?
等式12
?
四分之一波對稱性
當一個周期波形同時具有半波對稱性和偶/奇對稱性時,我們稱之為四分之一波對稱性。例如,圖3中的波形既具有半波對稱性,又具有均勻對稱性。另一方面,圖6中的波形是一個具有半波對稱性的奇異信號。因此,這兩個信號被稱為具有四分之一波的對稱性。
對于具有半波對稱性的偶數信號,由于偶數對稱性,所有 n 的 bn 系數都為零。此外,半波對稱性使 a0和偶數 n 的 an 系數消失。因此,對于具有半波對稱性的偶數信號,只有奇數 n 的系數可以是非零的。這些系數可以通過應用方程11找到,為方便起見,重復如下:
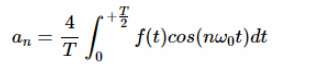
?
利用四分之一波對稱性,信號在正負半周期的中點附近表現出對稱性。因此,上述積分可簡化為:
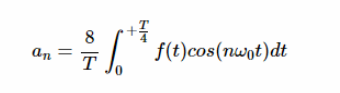
?
類似地,如果一個函數是奇數且具有半波對稱性,則由于奇對稱性,該函數的系數為零。同樣,a0是零,因為半波信號的平均值為零。由于信號的半波對稱性,只有奇數 n 的 bn 系數可以是非零的。對于單數 n,bn 由:
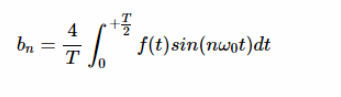
?
這也可以簡化為:
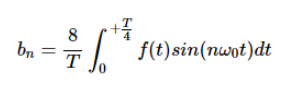
?
檢查兩種常見波形
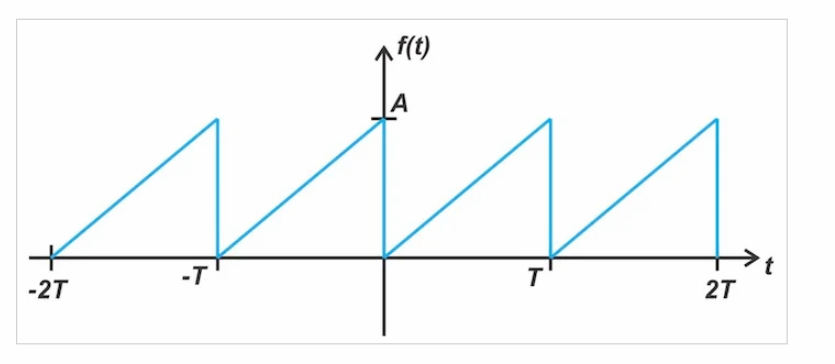
考慮圖8所示的鋸齒波形。
?
圖8。鋸齒波形的一個例子
?
使用方程1至3,上述波形可表示如下:
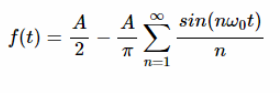
?
等式13
?
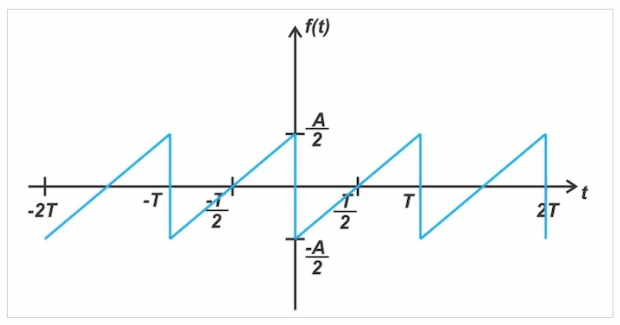
為了更容易地將波形與其傅里葉系數聯系起來,讓我們從信號中減去 DC 值,從而得到圖9中的波形。
?
圖9。從信號中減去 DC 值的奇函數波形實例
?
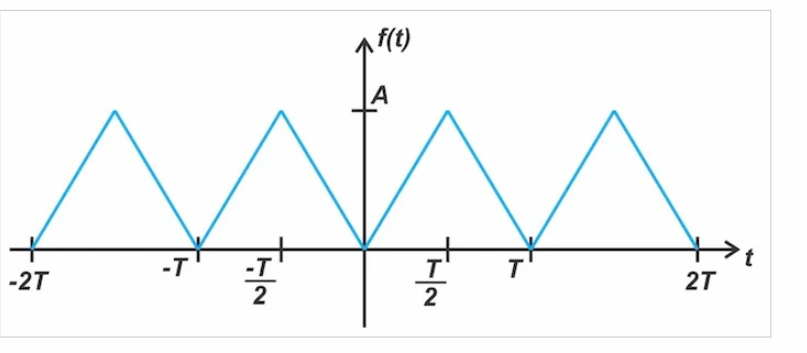
剔除直流值,得到一個奇函數。因此,我們可以得出結論,只有 bn 系數可以是非零的,這與方程13是一致的。作為最后一個示例,我們將查看如圖10所示的三角波。
?
圖10。一個示例三角波
?
函數的傅里葉級數表示如下:
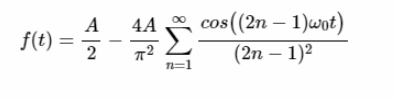
?
等式14
?
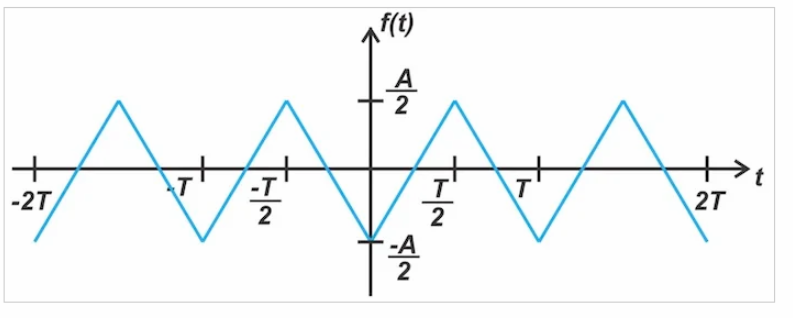
同樣,通過減去平均值,我們可以得到圖11中的波形。
?
圖11。半波對稱波形
?
在這種情況下,我們得到了一個具有半波對稱性的偶數信號。因此,對于所有 n,我們應該有 bn = 0; 對于偶數 n,我們應該有 an = 0。這與方程式14是一致的。
在本文中,我們探討了不同類型的對稱性對傅里葉系數的影響。有了這些知識,您現在應該能夠預測當信號具有某種類型的對稱性時,哪些系數將變為零。
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App































評論