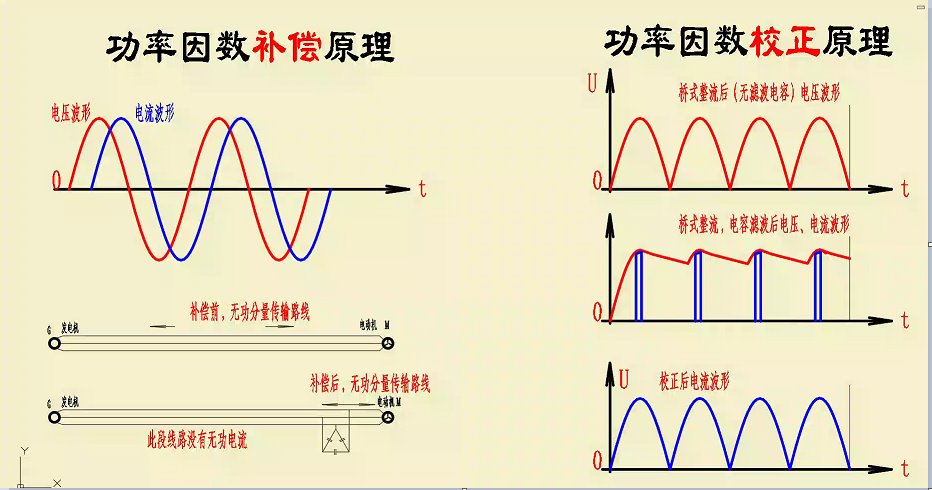
功率因數校正使用并聯電容器來對抗電感元件的影響并減少電壓和電流之間的相移。
功率因數校正是一種使用電容器降低交流電路的無功功率分量以提高其效率并降低電流的技術。
在處理直流 (DC) 電路時,連接負載消耗的功率可以簡單地計算為直流電壓乘以直流電流的乘積,即 V*I,以瓦特 (W) 為單位。對于固定的電阻負載,電流與施加的電壓成正比,因此電阻負載消耗的電功率將是線性的。但在交流 (AC) 電路中,情況略有不同,因為電抗會影響電路的行為。
對于交流電路,在任何時刻消耗的功率(以瓦特為單位)等于同一時刻的伏特和安培的乘積,這是因為交流電壓(和電流)是正弦曲線,因此幅度和電流都在不斷變化以由源頻率決定的速率隨時間變化的方向。
在直流電路中,平均功率只是 V*I,但交流電路的平均功率不是相同的值,因為許多交流負載都有電感元件,例如線圈、繞組、變壓器等。相位與電壓在一定程度上導致實際消耗的功率(以瓦特為單位)小于電壓和電流的乘積。這是因為在同時包含電阻和電抗的電路中,還必須考慮它們之間的相位角 (Θ)。
我們記得在關于正弦波形的教程中,相位角 (∠Θ) 是電流滯后于電壓的電度角。對于純電阻負載,電壓和電流是“同相”的,因為沒有電抗。
但是,對于包含電感器、線圈或螺線管或某種其他形式的感應負載的交流電路,其感應電抗 (X L ) 會產生一個相位角,電流滯后電壓 90度。因此,電阻 (R) 和感抗 (X L ) 均以歐姆為單位給出,其組合效應稱為阻抗。因此,由大寫字母 Z 表示的阻抗是由于電路電阻和電抗的綜合影響而以歐姆為單位給出的結果值。
考慮下面的 RL 串聯電路。
RL系列電路
由于它是串聯電路,因此電流必須為電阻器和電感器共用,因此電阻器上的電壓降 V R與串聯電流“同相”,而電感器上的電壓降 V L “超前”電流 90 o (ELI)。結果,電阻兩端的電壓降在電流矢量上,因為兩個矢量同相,而電感線圈兩端的電壓由于電壓超前電流 90 度而沿垂直方向繪制。
因此,為每個組件繪制的矢量圖將以電流矢量作為其參考,兩個電壓矢量相對于它們的位置被繪制,如圖所示。
R 和 L 矢量圖
電阻器電壓 V R沿水平或“實軸”繪制,電感器電壓 V L繪制在垂直或“虛軸”上。為了找到串聯電路上產生的電壓 V S ,我們必須使用電流作為參考來組合兩個單獨的矢量。使用畢達哥拉斯定理可以很容易地找到得到的矢量電壓,因為 V R和 V L的組合形成了一個直角三角形,如下所示。
RL 串聯電路的相量圖
由于畢達哥拉斯的方程 V2 S = V2 R + V2 L,V R和 V L的矢量和不僅給出了 V S的幅度,而且還給出了 V S和 I 之間的相角 (∠Θ) ,所以我們可以使用正弦、余弦和正切的任何一種標準三角函數來找到它。
功率因數校正示例 No1
RL 串聯電路由一個 15Ω 的電阻和一個感抗為 26Ω 的電感器組成。如果電路周圍流過 5 安培的電流,請計算:
1)電源電壓。
2)電源電壓和電路電流之間的相位角。
3) 繪制得到的相量圖。
1)。電源電壓 V S
我們可以使用電路的阻抗仔細檢查 150Vrms 的答案,如下所示:
2)。使用三角函數的相位角 Θ 為:
3)。得到的相量圖顯示 V S
電阻器(實部)兩端的計算電壓降為 75 伏,而電感器(虛部)產生的電壓為 130 伏。顯然,75 伏加 130 伏之和等于 205 伏,遠大于計算得出的 150 伏。這是因為 150V 的值代表相量和。了解各個電壓降和阻抗后,我們可以將這些值轉換為代表電路中實際或虛部消耗功率的值。
RL 串聯電路中的電源
在包含電抗的電路中,電流 i 將領先或落后于電壓一定量,具體取決于電抗是容性還是感性。電阻器消耗的功率(以瓦特為單位)稱為“實際功率”,因此用符號“ P ”(或W)表示。瓦特也可以計算為 I 2 R,其中 R 是電路的總電阻。但是,要根據 rms 電壓和 rms 電流 (V rms *I rms )計算有功功率的值,我們還必須將這些值乘以相位角的余弦值 cosΘ,得出:
有功功率,P = V*I cos(Θ)
因為,正如我們在上面看到的,電壓和電流對于電阻是“同相”的,因此相位角為零 (0),因此我們得到 cos(0) = 1。因此,將 V*I*1 相乘給我們與使用 I 2 R相同的實際功率值。然后使用上面的線圈示例,15Ω 電阻器消耗的功率為:
P R = I 2 R = 5 2 x 15 = 375 瓦
這與說:
P R = V R *I cos(Θ) = 75 x 5 x cos(0) = 375 瓦
當電壓和電流由于電路包含電抗而彼此“異相”時,V*I 的乘積稱為“視在功率”,單位為伏安 (VA) 而不是瓦特。伏安有符號“ S ”。對于純電感電路,電流滯后電壓 90 o,因此電感負載的無功功率為:V*I cos(+90 o ),變為:V*I*0。很明顯,電感沒有消耗功率,因此沒有功率損耗,因此 P L = 0 瓦。然而,為了表明這種無功功率存在于交流電路中,它被稱為無功電壓 (VAR),并被賦予符號“ Q“。因此,感應電路的無功伏安或簡單的“無功功率”使用符號Q L。
類似地,對于純容性電路,電流超前電壓 90 o,容性負載的無功功率為:V*I cos(-90 o ),它再次變為:V*I*0。很明顯,和以前一樣,電容沒有消耗功率,因此沒有功率損耗,因為 P C = 0 瓦。因此,為了表明這種無功功率存在于電容電路中,它被稱為伏安無功電容,并被賦予符號Q C。請注意,電容的無功功率定義為負值,即-Q C。
因此,再次使用上面的示例,以由頻率確定的速率流入和流出電感器的無功功率給出如下:
Q L = I 2 X L = 5 2 x 26 = 650 VAR
由于純電抗(感性或容性)中的電壓和電流波形之間存在 90 o的相位差,我們將 V*I 乘以 sin(Θ) 得到異相90 o的垂直分量。然而,角度的正弦 (sin 90 o ) 給出的結果為“1”,因此我們可以通過簡單地將 rms 電壓和電流值相乘來找到無功功率,如圖所示。
Q L = I 2 X L = V*I*sin(Θ) = 130*5*sin(90 o ) = 130*5*1 = 650 VAR
然后我們可以看到伏安無功或 VAR 部分具有幅度(與有功功率相同)但沒有與之相關的相位角。即無功功率始終在 90度垂直軸上。因此,如果我們知道:
P R = I 2 R = 375 瓦
和
Q L = I 2 X L = 650 VAR (ind.)
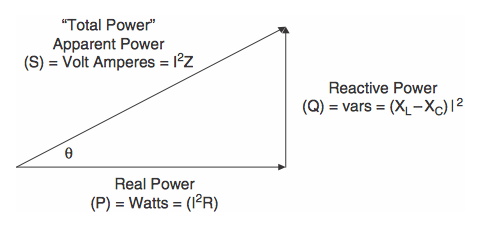
我們可以構造一個冪三角形來顯示 P、Q 和 S 之間的關系,如圖所示。
感應功率三角
電容功率三角
同樣,我們可以使用前面的畢達哥拉斯定理和正弦、余弦和正切的三角函數來定義冪三角形。
冪三角方程
功率因數校正示例 No2
一個線圈的電阻為 10Ω,電感為 46mH。如果它在連接到 100Vrms、60Hz 電源時消耗 5 安培的電流,請計算:
1) 元件兩端的電壓。
2)電路的相角。
3)串聯RL電路消耗的不同功率。
首先找到阻抗
1)。電阻器 V R和電感器 V L兩端的電壓
2)。電路的相位角
3)。電路電源
添加與線圈并聯的電容器不僅會減少這種不需要的無功功率,還會減少從電源獲取的電流總量。理論上,電容器可以提供電路所需的 100% 補償無功功率,但實際上,95% 到 98%(0.95 到 0.98)之間的功率因數校正通常就足夠了。因此,使用上面示例 2 中的線圈,需要多大的電容器才能將功率因數從 0.5 提高到 0.95。
0.95 的功率因數等于相位角: cos(0.95) = 18.2 o因此所需的 VAR 量為:
因此,對于 18.2 o的相角,我們需要 82.2VAR 的無功功率值。如果原始未校正的 VAR 值為 433VAR,而新計算的值為 82.2VAR,我們需要減少 433 – 82.2 = 350.8 VAR(電容)。所以:
將無功功率降低到 82.2VAR 所需的電容器在額定電源頻率下必須具有 28.5Ω 的容抗。因此電容器的電容計算如下:
因此,要將示例 2 中線圈的功率因數從 0.5 提高到 0.95,需要并聯一個 93uF 的電容器。使用上面的值,我們現在可以計算應用功率因數校正后電源提供的實際功率量。
新的伏安值
我們還可以構建一個冪三角形來顯示 VA (S) 和 VAR (Q) 的前后值,如圖所示。
冪三角
如果電路的視在功率從 500VA 降低到僅 263VA,我們可以計算提供的 rms 電流為:
S = V*I,因此: I = S/V = 263/100 = 2.63 安培
因此,只需在線圈上連接一個電容器,不僅可以將其總功率因數從 0.5 提高到 0.95,而且將電源電流從 5 安培降低到 2.63 安培,降低了約 47%。最終電路將如下所示。
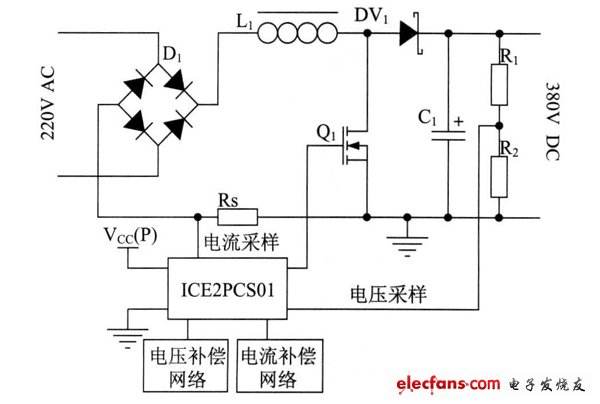
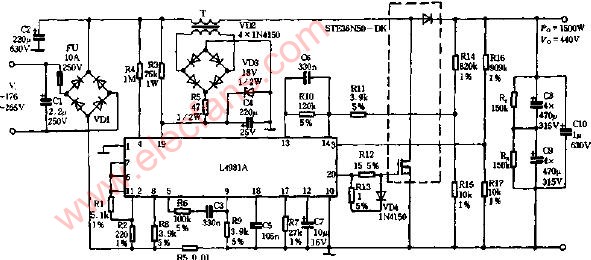
功率因數校正電路
我們在本教程中看到,由于電感負載導致的滯后功率因數會增加交流電路中的功率損耗。以電容的形式添加合適的容性無功元件與感性負載并聯,我們可以減小電壓和電流之間的相位差。這具有降低電路功率因數的效果,即有功功率與視在功率之比,以及改善電路的電能質量并減少所需的源電流量。這種技術稱為“功率因數校正”。
 電子發燒友App
電子發燒友App
























評論