量子比特是量子系統和量子力學某些元素的信息“比特”。但是量子比特是如何在物理上實現的呢？電子設備如何管理屬于量子生態系統的元素？在本文中，我們將開辟一條路徑來解釋您需要了解的有關數字量子電子學的所有信息。

量子

? ? ? ?位 經典的計算機位是 0 和 1，兩個位構成四種可能的狀態：00、01、10、11。通常，使用 n 個位，可以構建 2n 個不同的狀態。用 n 個量子比特可以得到多少個狀態？由 n 個量子比特系統生成的狀態空間的維度為 2n：在該空間中歸一化的每個向量代表一個可能的計算狀態，我們將其稱為 n 個量子比特的量子寄存器。量子比特數量的這種指數增長表明，量子計算機處理信息的速度可能比經典計算機高出指數級。請注意，對于 n = 200，您會得到一個大于宇宙中原子數的數字。

形式上，n 個量子位的量子寄存器是 2n 維希爾伯特空間 C2n 的一個元素，其計算基礎由 n 個量子位的 2n 個寄存器形成。讓我們考慮 2 個量子比特的情況。與單個量子比特類比，我們可以構建由向量 |00>、|01>、|10>、|11> 形成的狀態空間的計算基礎。具有 2 個量子位的量子寄存器是以下形式的重疊：

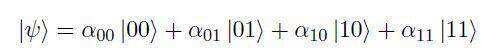
對系數的幅度進行歸一化。

邏輯端口

? ? ? ? 與經典計算機一樣，量子計算機由由基本量子邏輯門組成的量子電路組成。在經典情況下，只有一個（非平凡的）1 位邏輯端口，即 NOT 端口，它實現了通過真值表定義的邏輯否定運算，其中 1 → 0 和 0 → 1。

為了在量子位上定義類似的操作，我們不能將自己限制在確定其對主要狀態 |0> 和 |1> 的作用，但我們還必須指定處于狀態 |0> 和 | 重疊的量子位如何。 1> 必須轉型。直觀地說，NOT 應該交換兩個主要狀態的角色并將 α |0> + β |1> 轉換為 β |0> + α |1>。

很明顯，|0> 會變成 |1>，|1> 會變成 |0>。實現這種變換的操作是線性的，是量子力學的一般性質，在實驗上是合理的。

與量子 NOT 對應的矩陣因歷史原因而被稱為 X，其定義如下：

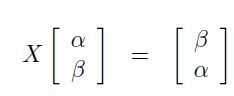
在歸一化條件下 |α|2 + |β|2 = 1 任何量子態 α |0> + β |1>。

除了 NOT 之外，Z 矩陣還表示了兩個重要的操作：

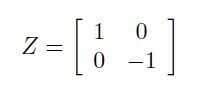
它只作用于組件 |1> 交換其符號和 Hadamard 端口：

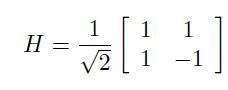
最后一個操作經常用于定義量子電路。它的作用是將基本狀態轉換為重疊，在計算基礎中進行測量后，以相等的概率產生 0 或 1。H 的影響可以定義為 NOT 執行一半，因此結果狀態既不是 0 也不是 1，而是兩個主要（基本）狀態的相干疊加。

在兩個經典位上實現操作的最重要的邏輯端口是 AND、OR、XOR、NAND 和 NOR 端口。NOT 和 AND 端口形成一個通用集；即，任何布爾函數都可以通過這兩個操作的組合來實現。出于同樣的原因，NAND 形成了一個通用集。

XOR 的量子等價物是受控非 (CNOT) 端口，它在 2 個量子位上運行：第一個是控制量子位，第二個是目標量子位。如果控件為 0，則目標保持不變；如果控件為 1，則目標被否定。那是：

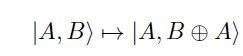
其中 A 是控制量子位，B 是目標，⊕ 是經典的 XOR 操作（圖 1）。

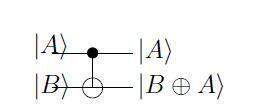
圖 1：CNOT 端口

圖 2：量子測量電路

圖 3：用于創建貝爾態的量子電路

另一個重要操作由圖 2中的符號表示，包括測量量子位 |ψ> = α |0>+β |1>。結果是一個經典位 M（用雙線表示），它將是 0 或 1。

CNOT 端口可用于創建糾纏態。圖 3中的電路為計算庫 |00>、|01>、|10>、|11> 的每個狀態生成一個特定的糾纏態。這些狀態，我們用 β00、β10、β01、β11 表示，稱為貝爾或 EPR 狀態（貝爾、愛因斯坦、波多爾斯基和羅森，他們首先發現了它們的非凡特性）。

量子 CMOS

? ? ? ?在現代數字計算機中對信息進行編碼的方式是通過集成電路內充當數字或模擬元件的微型晶體管上的電壓或電流。每個晶體管由能夠定義狀態 0（低電壓）或 1（高電壓）的總線尋址。

量子計算機有不同的相似之處，基本思想如圖? 所示。在該圖中，我們觀察到一個超導量子比特（也稱為 SQUID — 超導量子干涉裝置），它是量子計算機（量子“晶體管”）的基本元件。術語“干涉”是指電子，其行為類似于量子波中的波，干涉模式會產生量子效應。

在這種情況下，基本元素是鈮，而不是經典晶體管中的硅。該材料的特性允許電子表現得像量子比特。當金屬冷卻時，它被稱為超導體并開始顯示出量子力學效應。超導量子比特結構將兩種狀態編碼為指向相反方向的微小磁場。通過量子力學，我們可以控制定義為 +1 和 –1 或 |ψ> = α |0>+β |1> 的這些狀態。

通過稱為超導環路耦合器的元件，創建了一個多量子位處理器。可以通過將許多這些元素（例如量子位和耦合器）組合在一起來設計可編程量子設備。

為了控制量子位的運行，重要的是要有一個由約瑟夫森結組成的開關結構，該結構可以引導每個量子位（將磁信息脈沖路由到芯片上的正確點）并將信息存儲在本地磁存儲元件中每個設備。

約瑟夫森效應是由絕緣結（稱為約瑟夫森結）隔開的兩個超導體之間產生的電流。該效應是由于每個超導體中電子對的隧道效應。如果絕緣子太寬，隧道效應的概率低，效應不會發生。

大多數約瑟夫森結代表一個量子處理單元 (QPU)。QPU 沒有大面積的內存（高速緩存），因為它們的設計更像是生物大腦，而不是傳統硅處理器的常見馮諾依曼架構。人們可以將量子比特視為神經元，將耦合器視為控制這些神經元之間信息流動的突觸。

成功實現量子的要求包含在量子比特數中，量子比特數必須足夠大才能實現高效率。這也意味著你必須能夠在短時間內執行大量的量子比特操作。這些算法需要在許多量子位上應用許多邏輯門。為了保持錯誤的概率足夠低，門必須非常精確。

審核編輯：湯梓紅