了解半導體價帶和導帶的形成機制對于新材料生產的潛在技術影響至關重要。這項工作提出了一種寬帶隙計算模型，突出了理解能帶結構的理論困難，然后將其與實驗數據進行了比較。

我們通過提到寬帶隙碳化硅的晶體結構來結束之前的工作。特別是，我們研究了具有面心立方的所謂 β 形式，如圖 1 所示。

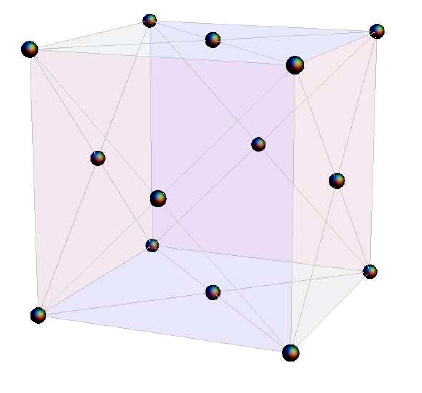
圖 1：β-SiC 的晶體結構

另一方面，寬帶隙氮化鎵具有更復雜的晶體結構，即纖鋅礦，一種由鋅和鐵組成的礦物。結合鋅和鐵原子的基本結構是六方結構;Mathematica 軟件返回六角晶格，如圖 2 所示。為此，必須添加硫化物結構，如圖 3 所示。

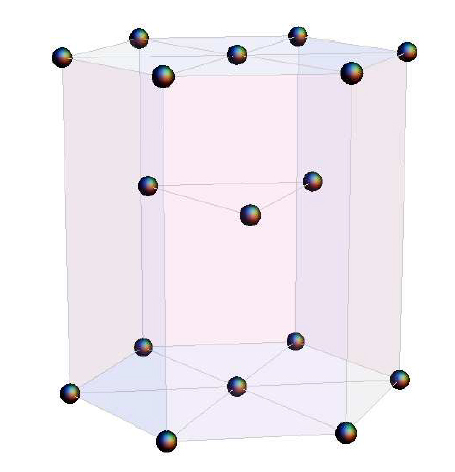
圖 2：六角晶格

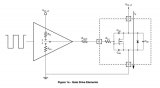
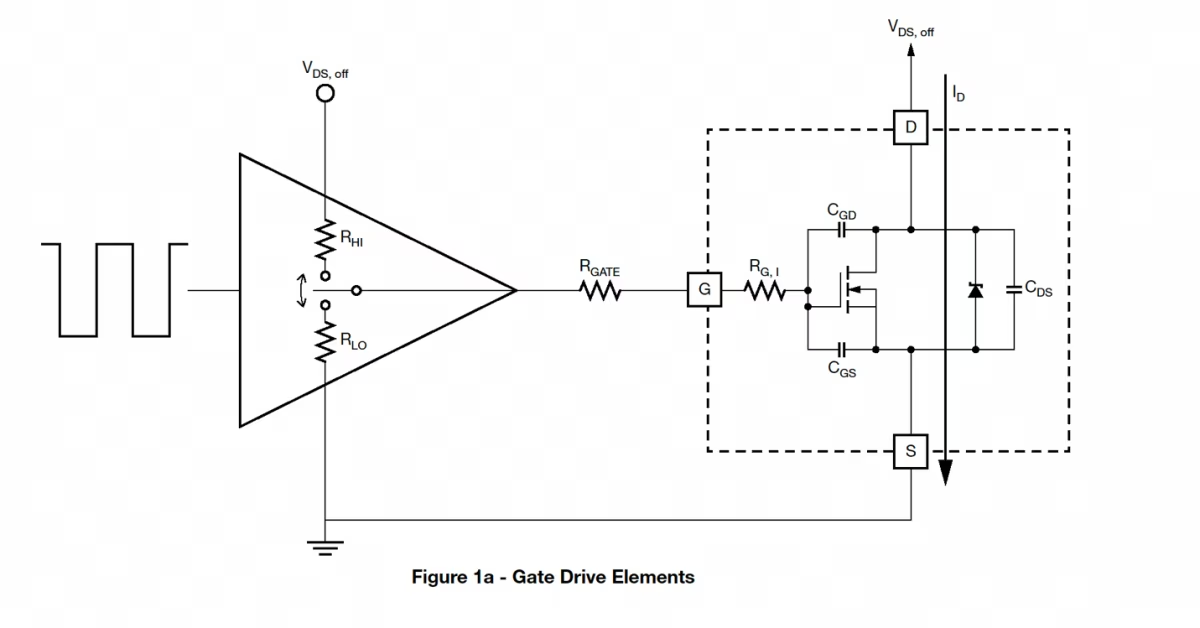
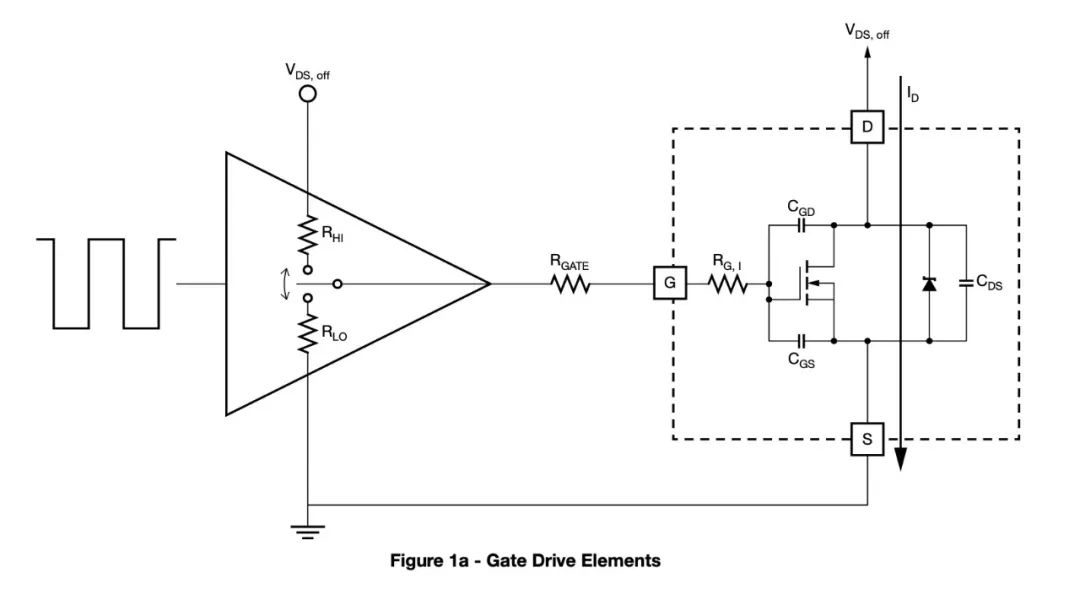
從晶格的周期性來看，我們期望固體的材料成分(原子/離子/電子)具有同樣的周期性行為，這將不得不考慮量子效應。在這個建模中，寬帶隙的計算困難是巨大的，如圖 4 和 5 所示的圖表所示。1第一張圖很明顯，而第二張圖說明了鍺帶隙是一個新量 k 的函數，稱為波向量。由于電子本身的波動性，后者表達了與晶體結構有關的單電子的周期性行為。

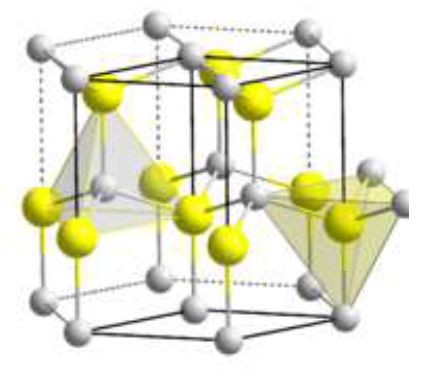
圖3：纖鋅礦的晶格(來源：Italiawiki)

圖 5 中的圖表可以追溯到 1960 年代，緊隨其后的是主要在硅和鍺上進行的理論和實驗工作的密集交叉。

在下一節中，我們提出了一個簡單的模型，該模型突出了以下特點：

與原子的平均尺寸相當的晶格參數值有利于允許帶的起源。這是由于構成固體的原子密度的增加，這對應于有利于原子本身電離的能量的增加，因此在任何情況下都限制在晶格中的自由電子(開玩笑地，它們受布洛赫波的束縛)使自己負責電荷的傳輸

盡管看起來很矛盾，一個完全占據的能帶(從某種意義上說，對于每個能級，根據泡利不相容原理，我們發現兩個具有反平行自旋的電子)不會傳導電流。這是由于電子的波動性質：電子波的疊加/干擾的“游戲”返回(在全波段)駐波，眾所周知，駐波不具有傳播特性。

圖 4：半導體中能帶的通用示意圖(來源：Kittel C. Introduction To Solid State Physics)

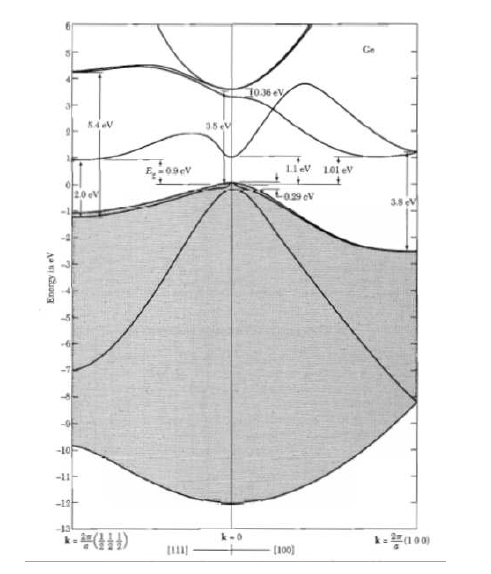
圖 5：鍺的能帶與 k 的函數關系(來源：Kittel C., Introduction To Solid State Physics)

1023個氫原子組成的虛擬導體

現在，我們不再研究寬禁帶 SiC 和 GaN 等復雜且奇異的晶格，而是將立方晶格視為最簡單的晶格，以便進行計算實驗，其結論雖然不普遍，但提供了有價值的電荷傳輸現象的線索。

原子/離子/電子的位置將被稱為笛卡爾氧軸系統，如圖 6 所示。這里的原始向量具有相同的長度：

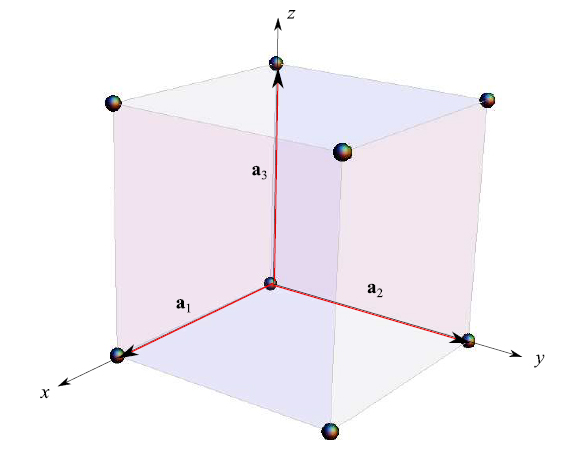
圖 6：其基本結構無限重復的立方晶格。

因此，我們有一個自由參數：晶格常數 a，即立方體的邊。

由于我們是在虛擬工作，我們向每個頂點“添加”一個氫原子，每個頂點位于

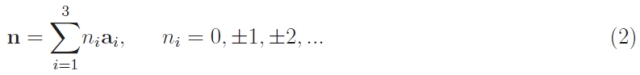
我們借用氫有兩個原因：它是最簡單的原子(一個質子和一個電子)，而且它是唯一一個以封閉形式求解決定電子量子態的薛定諤方程的原子。

我們考慮基本能級的單原子電子，它的能量是

從數量上講，具有這種能量的電子由波函數(稱為原子軌道)描述：

其中下標 1(在軌道和能量中)提醒我們我們正在考慮基本能級。自變量是電子的徑向坐標：

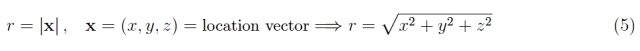
0 ? 0.5 埃 (1 埃 = 10 -8 cm ) 是定義

氫原子線性尺寸數量級的玻爾半徑。因此，電子的波動性質通過原子軌道表現為波函數，其解釋具有統計性質：其平方模量是找到具有指定徑向坐標的電子的概率密度。從基本能級波函數的解析表達式可以看出，這個概率在 r —> 0 時最大，然后隨著 r 的增加呈指數衰減。

因此，我們有無限的原子，每個原子都位于 x - n 中，其中單個電子處于量子態：

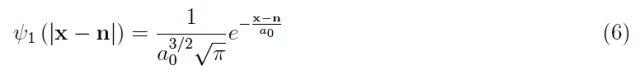
因為它通過庫侖勢與相應的質子結合：

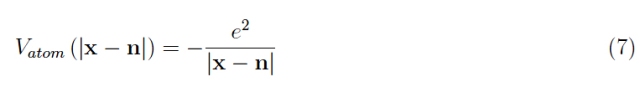
其中 e 是電子電荷的絕對值。總之，這個虛擬固體是通過在每個網狀位點上添加氫原子來組裝的，從一個極其稀薄的初始配置開始，即網狀間距 a >> a 0。這樣，各個軌道不會由于其各自幅度的指數衰減而重疊。然而，原子分布均勻，因此庫侖勢7分布均勻。由此產生的潛力如下：

其中總和擴展到整個晶格。因此，單個電子在與相應原子結合的同時“感受”到電位 V 0 (x)。后者是笛卡爾坐標x、y、z與晶格周期性的周期函數。對于布洛赫定理，單電子波函數是由具有晶格周期性的周期函數調制幅度的平面波。回想一下，平面波的空間部分屬于

其中 k = (k x , k y , k z ) 是傳播矢量(或波矢量)，其模量與波長的關系如下：

通常稱為波數，因為它返回線性維度為 λ 的區域中的振蕩次數。最好使用復雜的符號，將空間部分寫為

為了更好地定義由波向量定義的量子態，我們必須考慮一個實際情況，其中晶體具有有限擴展。這是一個大問題，因為它破壞了電位的周期性，因此破壞了應用布洛赫定理的可能性。幸運的是，可以通過應用所謂的周期性邊界條件(或以下稱為 Born-Karman，BK)來恢復周期性。理想情況下，考慮直線上的一維晶體，我們可以將該序列截斷為指定的長度 L = Na，其中 a 是晶格間距(相鄰原子之間的距離)。N 的數量級是 10 23，這讓人想起阿伏伽德羅數。

分布的周期性可以簡單地通過修改晶體拓撲結構或通過在 L = Na 處彎曲截斷的分布軸直到它在一個循環中閉合來恢復。這樣，即使我們無限次地循環，我們也能找到相同的分布。BK 的條件應用于截斷軸的極端，并且 cos(ka) 的存在迫使變量 k 采用離散值而不是連續值。除其他外，這個變量定義了一個“空間 k”，它是由晶格定義的空間的一種對偶，被稱為倒數格(細心的讀者會理解這兩個格子通過傅里葉變換連接)其中物理上重要的量(例如能量)表現出作為 k 函數的周期性行為，周期為 2π/a。所以，

稱為布里淵第一區或縮減區。如上所述，BK 的條件確定了 k 的采樣連續允許的和等距的 2π 值。允許值的數量等于 N;但是 N = 10 23我們有一個非常密集的值譜，即連續的。

剛剛提到的內容立即推廣到三維情況。更準確地說，(12) 被重寫為波矢量 k 的單個分量：

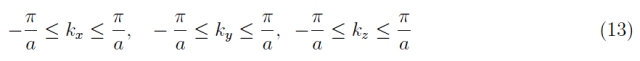
它定義了三維情況下的第一個布里淵區，它顯然展示了單個分量的離散采樣。在這里，我們有 N 3 個允許的三維向量 k 值。

因此，我們出現了一個新的量子數——波矢量 k。對于上述情況，單個電子的可能狀態等于 k 允許的值的數量，即 N 3然后將其乘以 2，等于每個 k 值的電子自旋態數(電子自旋被量化，并且只能假設兩個值定義反平行向量)。此外，根據布洛赫定理，單電子波函數是一個原子軌道ψ1，同時它必須是一個調幅平面波。使用一種暗示性但有效的語言，我們可以斷言電子通過線性組合穿過原子軌道，例如：

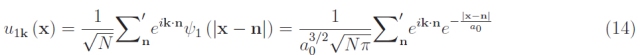
這又是一個布洛赫波函數(因為它是幅度調制的)。求和中的上標表示求和擴展到大小(每條邊)Na 的樣本。出現在求和前面的因素是歸一化(根據概率的定義)。只要它是 ? a0，軌道就不會重疊，并且電子盡管有 2N 3個可用狀態，但仍保持其能量 E 1 = -13.6 eV。但是，在虛擬晶體的實現中，我們必然要降低晶格參數，直到它與玻爾半徑a 0相當. 這導致了原子軌道的重疊，并且這種效應可以通過量子力學進行微擾處理。基本上，單個電子開始主要“感受”相鄰原子的庫侖勢。更具體地說，時間相關的微擾理論(在量子力學中廣為人知)返回 E 1能級在一組 2N 3值中的分裂，這些值構成一個幾乎連續的譜，每個譜對應于每個 k 值。我們有技術上稱為能帶的東西。

微擾理論以最小的非零階返回關于單個電子能量的以下結果：

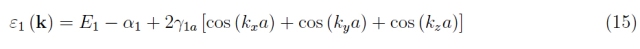
這里我們保留下標“1”，因為可以對氫原子的激發能級重復該過程(如果我們考慮軌道角動量為零的狀態，否則情況會變得更加復雜)。從計算中可以看出，α 1項是正的，因此以相反的符號出現確定了能量 E 1的下降。但有趣的術語是 γ 1a，它取決于晶格間距，是作為波矢量分量函數的正弦振蕩幅度。換言之，該項再現了寬帶隙晶格的周期性，因此，將未受擾動的能級 E 1分裂為 2N 3 個連續能級。否則(γ1a = 0) 單個電子的能量不依賴于 k，情況不會受到干擾。更詳細地說，這個量級是軌道疊加的積分，并且隨著晶格參數的減小而不為零。期限

具有振蕩幅度(圍繞 E 1 - α 1)等于 4 |γ 1a |，因此乘以維數3我們得到幅度 12 γ 1a，這是能帶的幅度。很明顯

因為我們將截斷的微擾發展應用于一階。函數的圖是一個三維超曲面(在四維空間中可見)，所以如果我們只滿足于一維我們得到

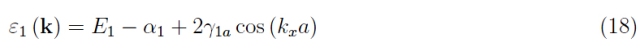
具有圖 7 類型的典型趨勢，顯示了一個能帶的形成。

如果我們使用 Mathematica 軟件逐步減少剩余的網狀步驟

上述微擾發展的有效性，我們得到圖 8 所示的圖形序列。在最后一個圖中，出現了一個能量區間 E > 0，這顯然對應于宏觀電子數的電離狀態。沒有違反能量守恒原理，因為電離的發生是以相鄰原子的存在所產生的微擾電勢為代價的。請注意，沒有必要施加電場來引起電荷位移，因為我們忽略了電子-晶格碰撞。正是后者，作為非彈性的，決定了動能的損失，因此決定了維持電流的可能性。

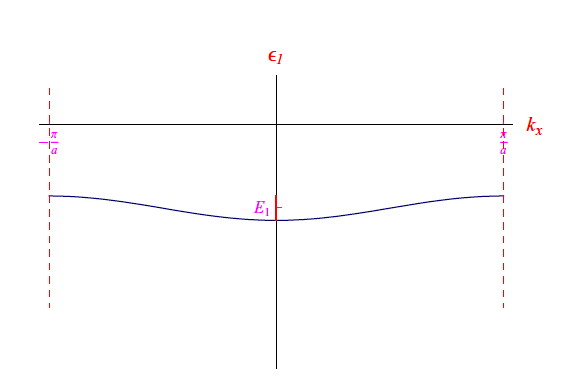
圖 7：將未受干擾的能級分成一個能帶。這是α1 = 0.1 eV，γ1a = -1 eV

因此，我們創建了一個虛擬導體，其中電子導電性是由于以庫侖能量為代價發生的電離過程。

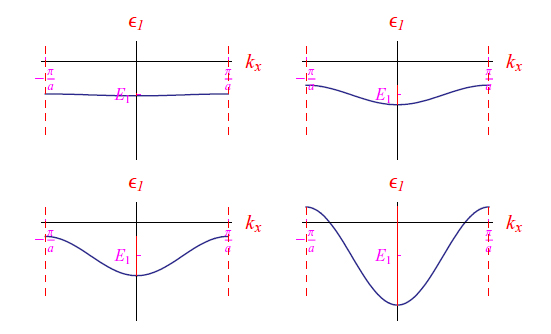
圖 8：為降低晶格參數值而分裂未受擾動的能級，直至形成導帶

與實驗數據比較

在這一點上，我們將圖 8 的圖表與圖 5 的圖表或再次與 GaAs 相關的圖表進行比較，如圖 9 所示，它顯示了函數 ε (k) 的對稱性被破壞的不規則趨勢

天真地，這可能是由于單個電子的能量分布規律作為其波矢量的函數的各向異性。事實上，在上一節的模型中，我們考慮了相對于真實導體/半導體的復雜性的簡單行為。

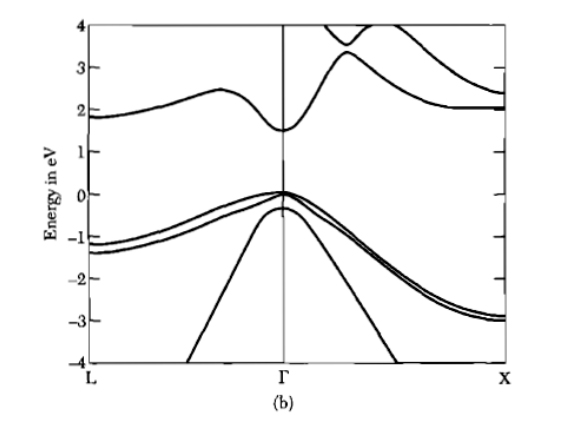
圖 9：GaAs 能帶。(來源：Kittel C.，《固態物理學導論》)

然后我們沒有考慮電子自旋，只記得我們有 2N 3而不是可用的 N 3狀態，特別是，自旋角動量和電子軌道角動量之間的相互作用被忽略了。要知道它是什么，有必要觀察我們在圖 5-9 中看到的各種分支表示不同軌道的分布 ε (k)，因此我們將方程 15 重寫為兩個連續的原子狀態 n，n + 1(不要將量子數 n 與晶格向量的模數混淆)。與符號的含義：

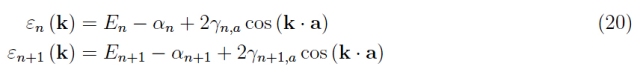
根據寬帶隙的定義：

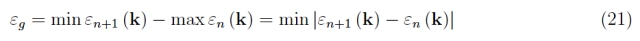
它遵循

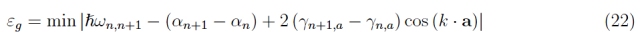
存在

也就是說，參考圖表和我們未在此處報告的硅的理論模型，考慮量子數 n 的原子態(任何激發態)，關于它們在角動量 l = 1 時的軌道部分，然后考慮自旋和軌道矩的合成規則(即自旋+軌道)，我們有 j = 3/2 和 j = 1/2，在光譜符號中用 p 3/2和 p 1/表示2. 從量子力學中，我們知道這些狀態是簡并的(前 4 次，后 2 次)，因為它們定義了物理上不同的狀態但具有相同的能量。然而，具有較高總角動量的狀態具有較高的能量(由于自旋軌道相互作用而產生的影響)。從同一張圖中，我們看到價帶的上極值在 k = 0 處(因此可以應用拋物線帶近似，正如我們將很快看到的那樣，它允許我們近似 ε (k))，而極k > 0 時導帶較低。從圖中，我們讀取了各個寬帶隙的值，在任何情況下都必須按如下方式更新：

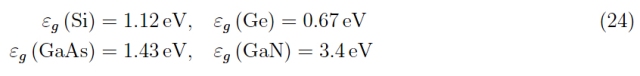
盡管過度簡化，提出的理論模型還是返回了有趣的結果。例如，在一維情況下，嚴格的數學分析顯示了圖 10 所示類型的能帶結構。

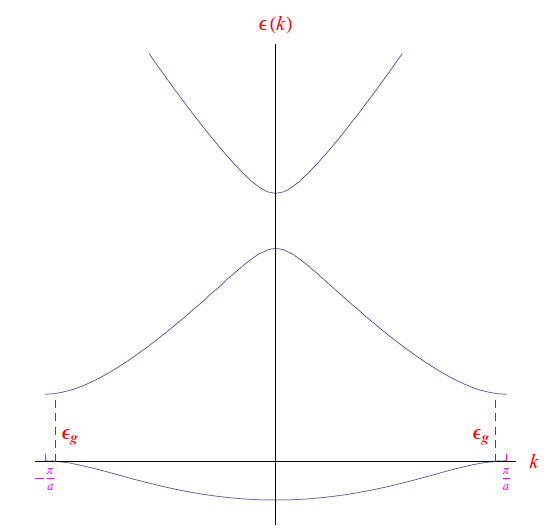
圖 10：簡單線性晶格鏈情況下的能帶，其中單個離子產生由變化的狄拉克 delta 表示的勢阱

因此，推導出色散定律 ε (k) 至關重要。這個面額來源于波浪力學;到目前為止，我們已經考慮了描述電子在固體中傳播的相應布洛赫波的“快照”。因此，我們必須添加時間依賴性。單色平面波的完整表達式為

并且用復雜的形式和角頻率來寫更方便：

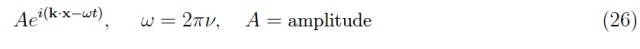
從舊量子理論(OQT)我們知道能量與頻率相關

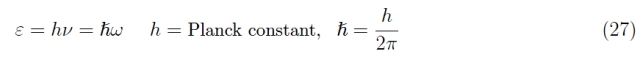
所以，

因為 ε 取決于 k。因此，我們有一個單色平面波的疊加形成一個波包，在一維情況下寫成

傳播速度(群速度)為

進而通過調節電子波運動的牛頓第二定律確定該粒子的有效質量，表示為

它的出現是由于晶體的周期性電位的存在。事實上，根據德布羅意假設 (OQT)，電子盡管可以通過波包的傳播來解釋，但它具有動量

準確地表達了波粒二象性。在上一期發現的色散定律中，a cos (ka)：

考慮到緊鄰零的 k 值，并將 cos(ka) 發展到泰勒級數的二階，我們有一個無關緊要的加性常數：

這正是能量對不受力的粒子動量的依賴性，在這種情況下，有效質量與電子的質量一致。事實上，這個簡單的論點告訴我們，晶體中電子的有效質量表示色散定律與(34)的偏差。只有在“能帶末端”，即 k - > 0 時，電子才大致不受周期勢的影響。換句話說，有效質量是允許根據經典力學處理電子的技巧。事實上，我們首先應用了波動力學，然后求助于牛頓第二定律。這種方法被稱為半經典近似。

最后，對電子能量 ε 分布的統計分析表明，如果一個能帶被完全占據，每個波包的群速度為零——沒有傳播，因為單個單色波的疊加返回一個駐波. 這意味著具有完全占據帶的固體是絕緣體。然而，這個結論一定不能誤導，因為它在一維情況下是有效的。其他兩個空間維度的出現可以確定關于能帶結構拓撲的非典型行為，因為可以為波矢量 k 的不同方向創建疊加，這會產生導體而不是絕緣體。然而，玩“骯臟游戲”的是最外層的電子。例如，由于最外層軌道的完全填充，鋅應該是絕緣體。然而，由于各個能帶的特定拓撲結構，已經產生了重疊，保證了攜帶電荷的可能性。

我們通過觀察寬帶隙測量主要用于：

霍爾效應

回旋共振

光譜學(特別是對于寬帶隙 GaN)。

寬帶隙碳化硅

寬帶隙碳化硅具有立方硫化鋅(cubic zinc sulfide)的網狀結構，而后者又來源于金剛石(面心立方，FCC)的網狀結構。Zn 原子排列在一個 FCC 晶格上，S 原子排列在另一個 FCC 晶格上(圖 11。來源：[1])。

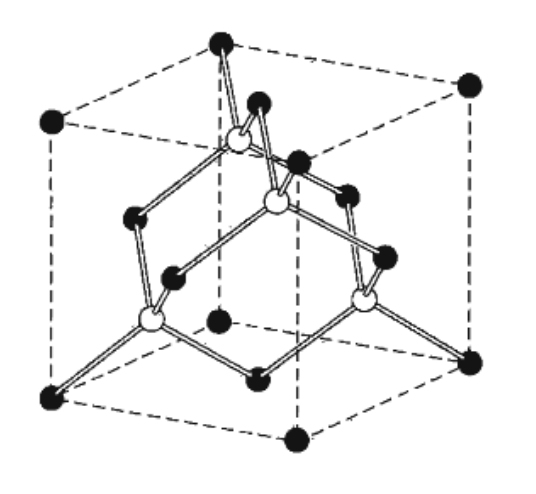
圖 11：立方硫化鋅的晶格結構

每個晶胞中有四個 ZnS 分子;在每個原子周圍，有四個不同種類的原子，它們等距排列在一個正四面體的頂點上。

觀察到在所有半導體(Si/Ge/SiC/GaN 等)中，晶格單個原子的最外層具有以下類型(光譜符號)是有益的：

其中 n 是主量子數，而 s 和 p 表示單電子軌道角動量狀態，分別等于 l = 0 和 l = 1。因此，我們有四個價電子形成了前一篇文章中已經研究過的共價鍵。這種鍵以熱能為代價被破壞，電子進入導帶。然而，這不是量子躍遷，而是溫度引起的統計機制。

寬帶隙 GaN

寬帶隙 GaN 的案例因其在光電子/光伏領域的技術效應而多樣化，這要歸功于能夠通過創建新的異質結構(例如 GaN 和氮化銦的混合物)來調節帶隙的可能性。目前，我們僅限于觀察寬帶隙 GaN 半導體標志著所謂的水分解技術的轉折點，即從水中提取氫氣，可用作燃料。[4]。

帶隙和溫度

我們已經有機會研究熱穩定性，因為帶隙不顯著依賴于半導體(Si/Ge/SiC/GaN)的熱力學平衡溫度 T，小于 10- 4 eV/K。事實上，已知[2]-[3]：

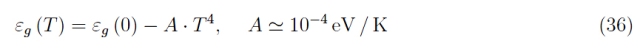
這種經驗關系在 [0, T ] 范圍內成立，其中 T ? Tmax 為

這是半導體表現得像導體的溫度。理論值，因為如此高的溫度會導致設備損壞。此外，一旦超過了指定的閾值溫度，我們的模型就不再有效，因為正如上一節所預期的，我們忽略了原子的運動。更準確地說，該模型基于 Born-Oppenheimer 近似，它將電子的運動與原子的運動分離，因為電子更輕，在原子運動的時間尺度上表現出幾乎瞬時的動態演化，由于熱能，它們在各自的平衡位置周圍執行“小”振蕩。隨著溫度升高，振蕩幅度增加，因此我們不能認為原子是“靜止的”。

一維情況下的布洛赫波——寬帶隙

在圖 12 中，我們報告了一維情況下的布洛赫波趨勢。具體來說，給定一個晶格的線性離子鏈，其中的電勢由周期函數表示：

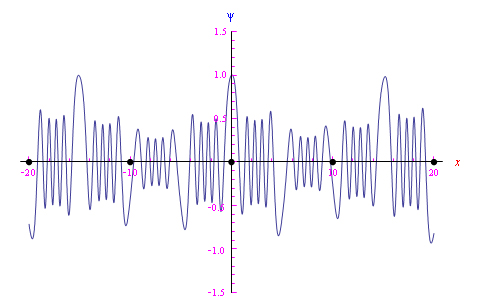
圖 12：線性晶格鏈的 Bloch 波狀解

在這種情況下，薛定諤方程以封閉形式求解，其解是 Mathieu 函數。

色散律的水平曲線

我們在圖 13 和 14 中報告了在情況 2-dim 中重寫的色散函數的水平曲線的形狀：

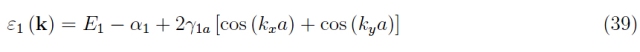
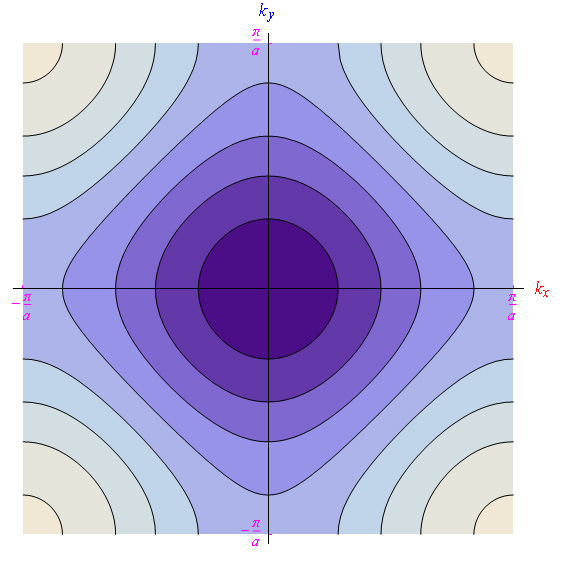
圖 13：等式 39 在第一布里淵區的等高線

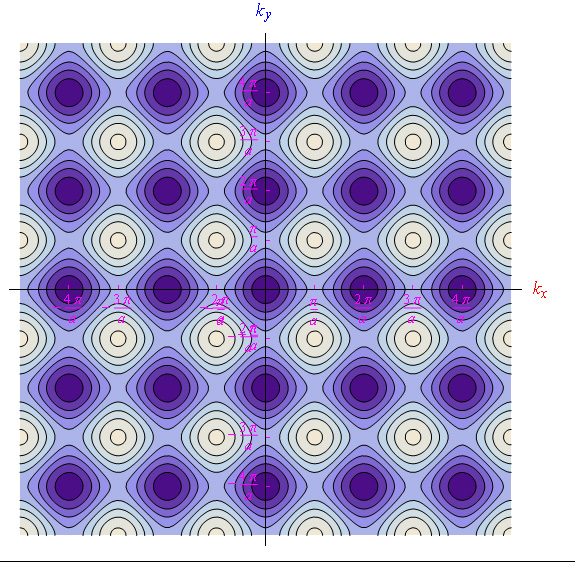
圖 14：擴展區域中方程 39 的輪廓

審核編輯：湯梓紅