PID控制算法的C語言實現一 PID算法原理
?? 最近兩天在考慮一般控制算法的C語言實現問題,發現網絡上尚沒有一套完整的比較體系的講解。于是總結了幾天,整理一套思路分享給大家。
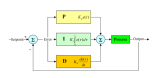
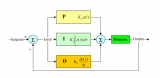
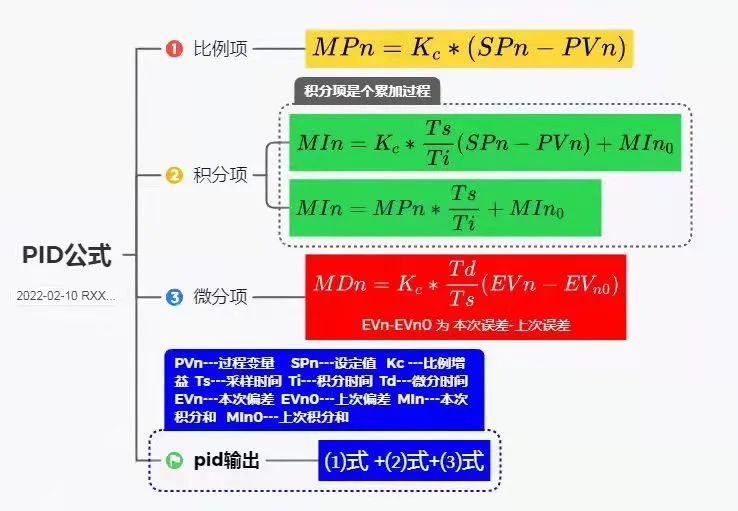
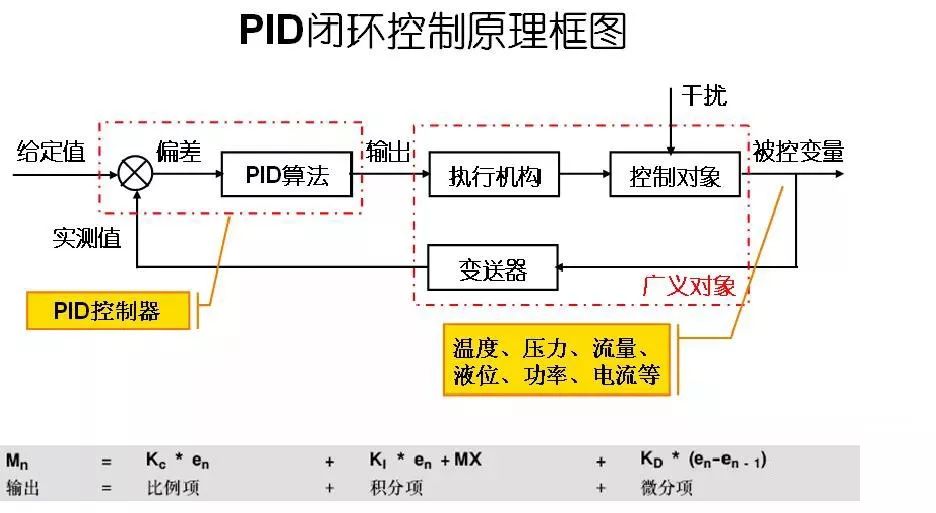
?? 在工業應用中PID及其衍生算法是應用最廣泛的算法之一,是當之無愧的萬能算法,如果能夠熟練掌握PID算法的設計與實現過程,對于一般的研發人員來講,應該是足夠應對一般研發問題了,而難能可貴的是,在我所接觸的控制算法當中,PID控制算法又是最簡單,最能體現反饋思想的控制算法,可謂經典中的經典。經典的未必是復雜的,經典的東西常常是簡單的,而且是最簡單的,想想牛頓的力學三大定律吧,想想愛因斯坦的質能方程吧,何等的簡單!簡單的不是原始的,簡單的也不是落后的,簡單到了美的程度。先看看PID算法的一般形式:
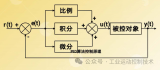
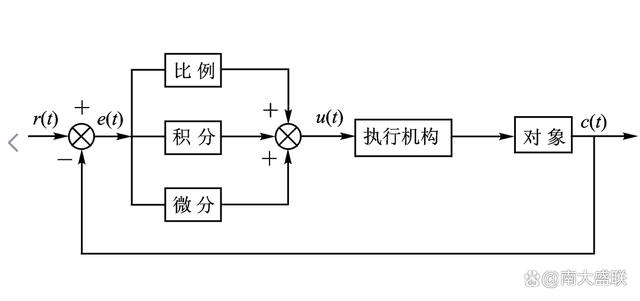
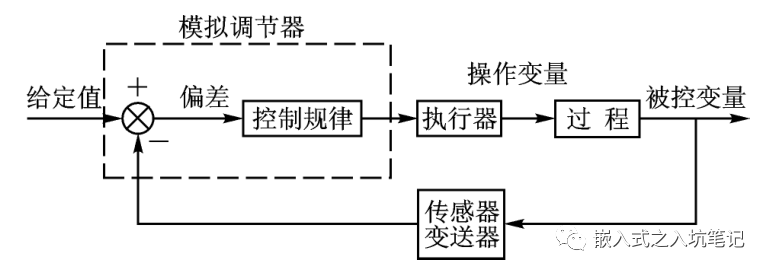
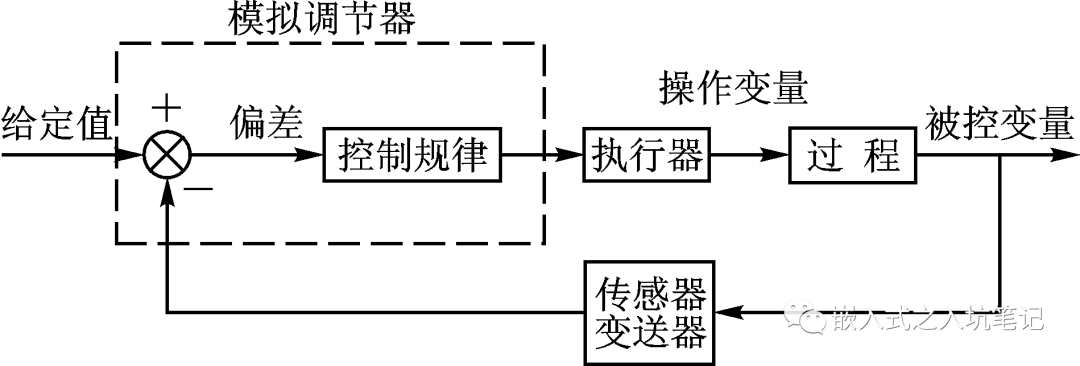
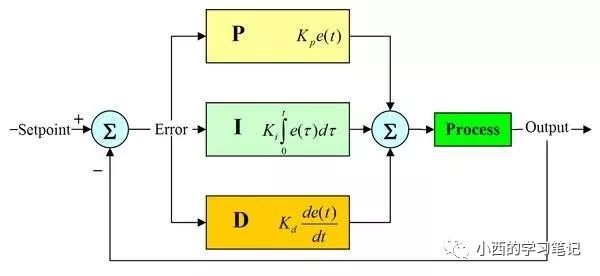
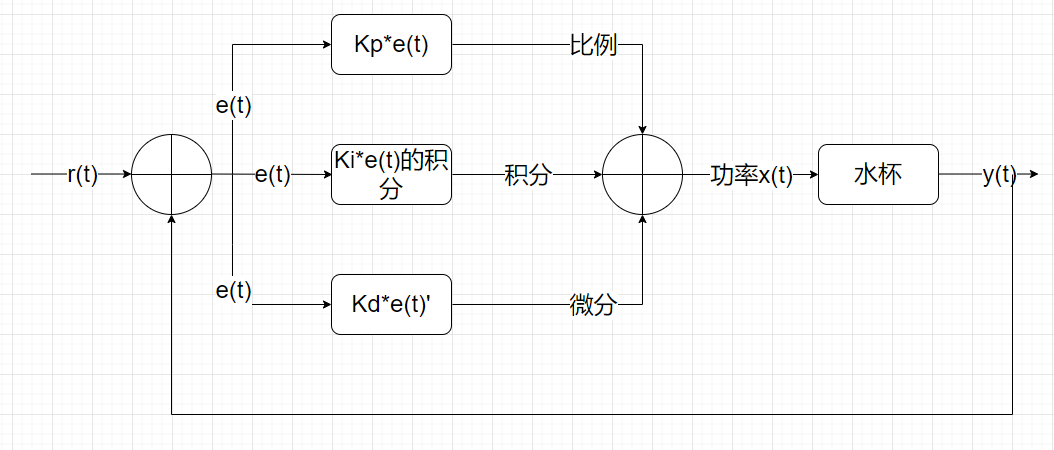
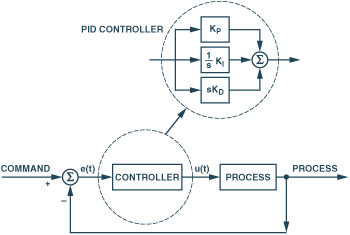
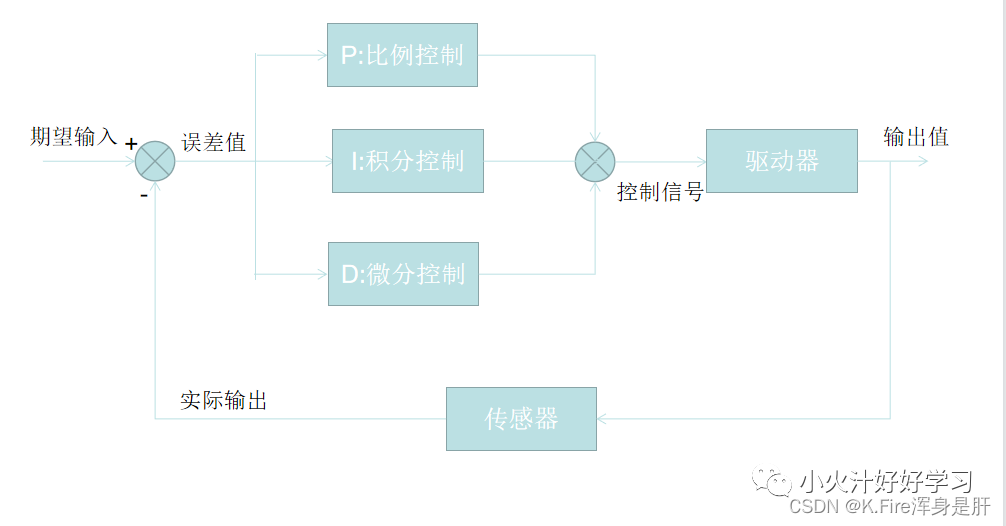
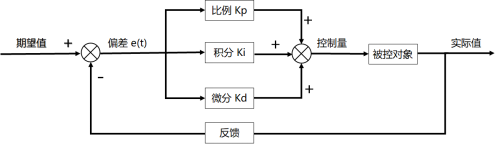
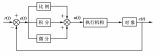
?? PID的流程簡單到了不能再簡單的程度,通過誤差信號控制被控量,而控制器本身就是比例、積分、微分三個環節的加和。這里我們規定(在t時刻):
?? 1.輸入量為rin(t);
?? 2.輸出量為rout(t);
?? 3.偏差量為err(t)=rin(t)-rout(t);
?? pid的控制規律為
?? 理解一下這個公式,主要從下面幾個問題著手,為了便于理解,把控制環境具體一下:
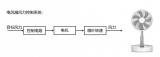
?? 1.規定這個流程是用來為直流電機調速的;
?? 2.輸入量rin(t)為電機轉速預定值;
?? 3.輸出量rout(t)為電機轉速實際值;
?? 4.執行器為直流電機;
?? 5.傳感器為光電碼盤,假設碼盤為10線;
?? 6.直流電機采用PWM調速?轉速用單位?轉/min?表示;
? 不難看出以下結論:
?? 1.輸入量rin(t)為電機轉速預定值(轉/min);
?? 2. 輸出量rout(t)為電機轉速實際值(轉/min);
?? 3.偏差量為預定值和實際值之差(轉/min);
???那么以下幾個問題需要弄清楚:
?? 1.通過PID環節之后的U(t)是什么值呢?
?? 2.控制執行器(直流電機)轉動轉速應該為電壓值(也就是PWM占空比)。
?? 3.那么U(t)與PWM之間存在怎樣的聯系呢?
http://blog.21ic.com/user1/3407/archives/2006/33541.html(見附錄1)這篇文章上給出了一種方法,即,每個電壓對應一個轉速,電壓和轉速之間呈現線性關系。但是我考慮這種方法的前提是把直流電機的特性理解為線性了,而實際情況下,直流電機的特性絕對不是線性的,或者說在局部上是趨于線性的,這就是為什么說PID調速有個范圍的問題。具體看一下http://articles.e-works.net.cn/component/article90249.htm(見附錄2)這篇文章就可以了解了。所以在正式進行調速設計之前,需要現有開環系統,測試電機和轉速之間的特性曲線(或者查閱電機的資料說明),然后再進行閉環參數整定。這篇先寫到這,下一篇說明連續系統的離散化問題。并根據離散化后的特點講述位置型PID和增量型PID的用法和C語言實現過程。
PID控制算法的C語言實現二 PID算法的離散化
?? 上一節中,我論述了PID算法的基本形式,并對其控制過程的實現有了一個簡要的說明,通過上一節的總結,基本已經可以明白PID控制的過程。這一節中先繼續上一節內容補充說明一下。
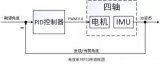
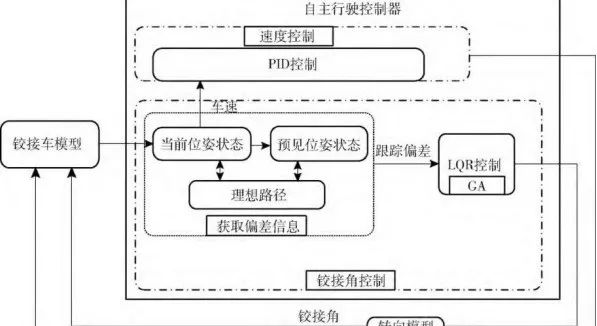
?? 1.說明一下反饋控制的原理,通過上一節的框圖不難看出,PID控制其實是對偏差的控制過程;
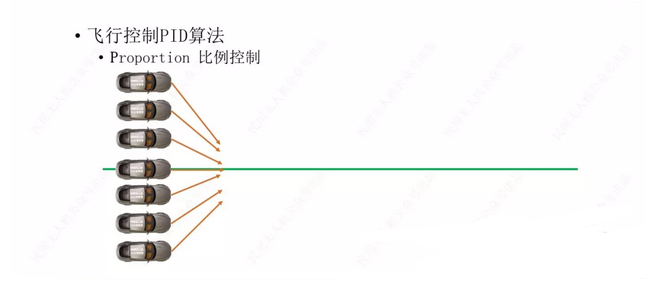
?? 2.如果偏差為0,則比例環節不起作用,只有存在偏差時,比例環節才起作用。
?? 3.積分環節主要是用來消除靜差,所謂靜差,就是系統穩定后輸出值和設定值之間的差值,積分環節實際上就是偏差累計的過程,把累計的誤差加到原有系統上以抵消系統造成的靜差。
?? 4.而微分信號則反應了偏差信號的變化規律,或者說是變化趨勢,根據偏差信號的變化趨勢來進行超前調節,從而增加了系統的快速性。
?? 好了,關于PID的基本說明就補充到這里,下面將對PID連續系統離散化,從而方便在處理器上實現。下面把連續狀態的公式再貼一下:
?? 假設采樣間隔為T,則在第K?T時刻:
偏差err(K)=rin(K)-rout(K);
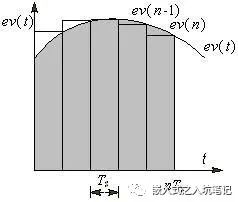
積分環節用加和的形式表示,即err(K)+err(K+1)+……;
微分環節用斜率的形式表示,即[err(K)-err(K-1)]/T;
從而形成如下PID離散表示形式:
則u(K)可表示成為:
至于說Kp、Ki、Kd三個參數的具體表達式,我想可以輕松的推出了,這里節省時間,不再詳細表示了。
其實到這里為止,PID的基本離散表示形式已經出來了。目前的這種表述形式屬于位置型PID,另外一種表述方式為增量式PID,由U上述表達式可以輕易得到:
那么:
這就是離散化PID的增量式表示方式,由公式可以看出,增量式的表達結果和最近三次的偏差有關,這樣就大大提高了系統的穩定性。需要注意的是最終的輸出結果應該為
???????u(K)+增量調節值;
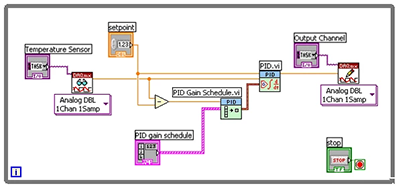
PID的離散化過程基本思路就是這樣,下面是將離散化的公式轉換成為C語言,從而實現微控制器的控制作用。
PID控制算法的C語言實現三 位置型PID的C語言實現
?? 上一節中已經抽象出了位置性PID和增量型PID的數學表達式,這一節,重點講解C語言代碼的實現過程,算法的C語言實現過程具有一般性,通過PID算法的C語言實現,可以以此類推,設計其它算法的C語言實現。
?? 第一步:定義PID變量結構體,代碼如下:
struct _pid{
?? ?float SetSpeed;?? ??? ??? ?//定義設定值
?? ?float ActualSpeed;?? ??? ?//定義實際值
?? ?float err;?? ??? ??? ??? ?//定義偏差值
?? ?float err_last;?? ??? ??? ?//定義上一個偏差值
?? ?float Kp,Ki,Kd;?? ??? ??? ?//定義比例、積分、微分系數
?? ?float voltage;?? ??? ???//定義電壓值(控制執行器的變量)
?? ?float integral;?? ??? ??? ?//定義積分值
}pid;
控制算法中所需要用到的參數在一個結構體中統一定義,方便后面的使用。
? 第二部:初始化變量,代碼如下:
void PID_init(){
?? ?printf("PID_init begin \n");
?? ?pid.SetSpeed=0.0;
?? ?pid.ActualSpeed=0.0;
?? ?pid.err=0.0;
?? ?pid.err_last=0.0;
?? ?pid.voltage=0.0;
?? ?pid.integral=0.0;
?? ?pid.Kp=0.2;
?? ?pid.Ki=0.015;
?? ?pid.Kd=0.2;
?? ?printf("PID_init end \n");
}
統一初始化變量,尤其是Kp,Ki,Kd三個參數,調試過程當中,對于要求的控制效果,可以通過調節這三個量直接進行調節。
第三步:編寫控制算法,代碼如下:
float PID_realize(float speed){
??? pid.SetSpeed=speed;
??? pid.err=pid.SetSpeed-pid.ActualSpeed;
??? pid.integral+=pid.err;
????pid.voltage=pid.Kp*pid.err+pid.Ki*pid.integral+pid.Kd*(pid.err-pid.err_last);
??? pid.err_last=pid.err;
??? pid.ActualSpeed=pid.voltage*1.0;
??? return pid.ActualSpeed;
}
注意:這里用了最基本的算法實現形式,沒有考慮死區問題,沒有設定上下限,只是對公式的一種直接的實現,后面的介紹當中還會逐漸的對此改進。
?? 到此為止,PID的基本實現部分就初步完成了。下面是測試代碼:
int main(){
??? printf("System begin \n");
??? PID_init();
??? int count=0;
??? while(count<1000)
??? {
??? ??? float speed=PID_realize(200.0);
??? ??? printf("%f\n",speed);
??? ??? count++;
??? }
return 0;
}
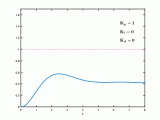
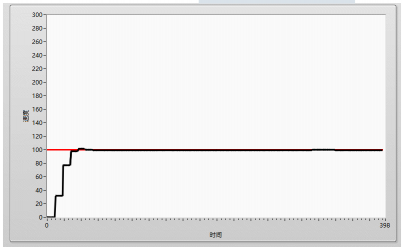
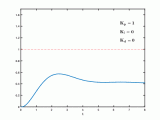
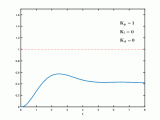
下面是經過1000次的調節后輸出的1000個數據(具體的參數整定過程就不說明了,網上這種說明非常多):
83.000001?11.555000?59.559675?28.175408?52.907421?38.944152 51.891699?46.141651 53.339054?51.509998?55.908450?55.944631?58.970680 59.882936?62.225001?63.537254?65.527707 ? 67.011058 68.810646 70.355318 72.042040 ? 73.595658?75.207620 76.745444 78.301526?79.812136?81.321929?82.800304 84.268909?85.71310??887.143455?88.553005?89.946960 91.322078?92.680996?94.022234 95.347186 96.655242 97.947180 99.222808 100.482601 101.726572
102.955049
104.168125
105.366066
106.549019
107.717187
108.870756
110.009898
111.134811
112.245652
113.342615
114.425860
115.495564
116.551897
117.595029
118.625116
119.642331
120.646826
121.638767
122.618307
123.585603
124.540813
125.484079
126.415549
127.335383
128.243715
129.140691
130.026459
130.901149
131.764909
132.617870
133.460162
134.291942
135.113308
135.924419
136.725382
137.516332
138.297401
139.068697
139.830352
140.582499
141.325237
142.058701
142.782985
143.498218
144.204509
144.901969
145.590726
146.270843
146.942486
147.605718
148.260674
148.907425
149.546109
150.176794
150.799612
151.414626
152.021959
152.621696
153.213951
153.798781
154.376315
154.946626
155.509812
156.065958
156.615146
157.157471
157.693012
158.221871
158.744097
159.259826
159.769078
160.271991
160.768588
161.258996
161.743264
162.221494
162.693737
163.160075
163.620593
164.075347
164.524422
164.967877
165.405795
165.838235
166.265257
166.686967
167.103377
167.514610
167.920681
168.321682
168.717670
169.108719
169.494862
169.876198
170.252740
170.624605
170.991799
171.354406
171.712487
172.066080
172.415265
172.760077
173.100594
173.436838
173.768895
174.096796
174.420594
174.740352
175.056096
175.367915
175.675818
175.979886
176.280136
176.576656
176.869444
177.158600
177.444121
177.726087
178.004510
178.279458
178.550967
178.819094
179.083860
179.345315
179.603504
179.858466
180.110241
180.358866
180.604388
180.846849
181.086262
181.322699
181.556172
181.786733
182.014396
182.239222
182.461226
182.680475
182.896971
183.110768
183.321881
183.530369
183.736239
183.939545
184.140301
184.338555
184.534321
184.727651
184.918558
185.107080
185.293243
185.477080
185.658625
185.837886
186.014930
186.189745
186.362382
186.532859
186.701207
186.867437
187.031605
187.193713
187.353802
187.511884
187.667997
187.822151
187.974384
188.124700
188.273148
188.419728
188.564488
188.707429
188.848592
188.987995
189.125644
189.261576
189.395801
189.528364
189.659258
189.788528
189.916170
190.042233
190.166702
190.289633
190.411007
190.530867
190.649236
190.766119
190.881544
190.995531
191.108087
191.219243
191.329005
191.437382
191.544428
191.650111
191.754504
191.857565
191.959350
192.059857
192.159119
192.257135
192.353919
192.449511
192.543890
192.637105
192.729137
192.820032
192.909776
192.998410
193.085920
193.172360
193.257700
193.341993
193.425214
193.507408
193.588568
193.668715
193.747847
193.826004
193.903175
193.979391
194.054643
194.128963
194.202349
194.274828
194.346393
194.417073
194.486854
194.555777
194.623820
194.691027
194.757390
194.822919
194.887626
194.951536
195.014633
195.076965
195.138496
195.199273
195.259270
195.318547
195.377060
195.434856
195.491918
195.548283
195.603919
195.658886
195.713145
195.766734
195.819654
195.871912
195.923517
195.974472
196.024791
196.074478
196.123558
196.172016
196.219859
196.267115
196.313778
196.359851
196.405363
196.450296
196.494672
196.538492
196.581753
196.624494
閱讀全文
 電子發燒友App
電子發燒友App









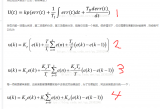




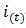
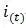
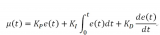





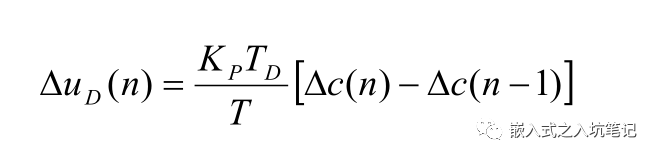





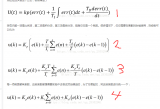










評論