N-最短路徑 是中科院分詞工具NLPIR進行分詞用到的一個重要算法,張華平、劉群老師在論文《基于N-最短路徑方法的中文詞語粗分模型》中做了比較詳細的介紹。該算法算法基本思想很簡單,就是給定一待處理字串,根據詞典,找出詞典中所有可能的詞,構造出字串的一個有向無環圖,算出從開始到結束所有路徑中最短的前N條路徑。因為允許相等長度的路徑并列,故最終的結果集合會大于或等于N。
根據算法思想,當我們拿到一個字串后,首先構造圖,接著針對圖計算最短路徑。下面以一個例子“他說的確實在理”進行說明,開始為了能夠簡單說明,首先假設圖上的邊權值均為1。?
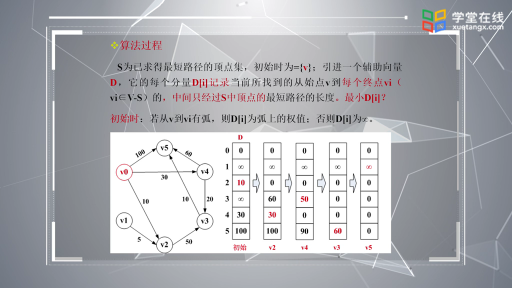
先給出對這句話的3-最短路(即路徑最短的前3名, 因為有并列成分, 所以可能候選路徑大于3)徑求解過程圖:?
從節點4開始, 因為4是第一個出現多個前驅節點的
?
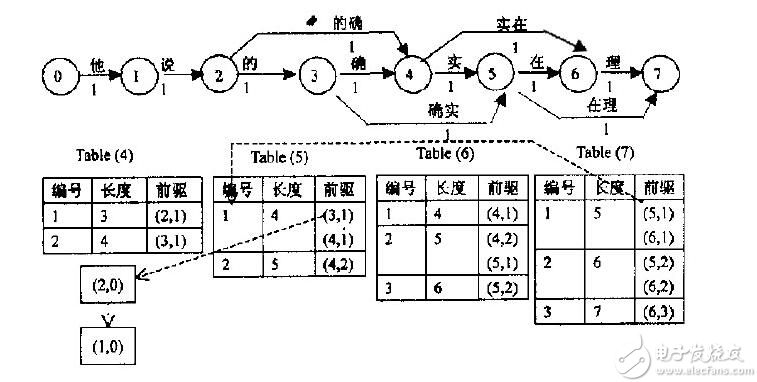
首先看圖中上方,它是根據一個已有詞典構造出的有向無環圖。它將字串分為單個的字,每個字用圖中相鄰的兩個結點表示,故對于長度為n的字串,需要n+1個結點。兩節點間若有邊,則表示兩節點間所包含的所有結點構成的詞,如圖中結點2、3、4構成詞“的確”。
圖構造出來后,接下來就要計算最短路徑,N-最短路徑是基于Dijkstra算法的一種簡單擴展,它在每個結點處記錄了N個最短路徑值與該結點的前驅,具體過程如上圖中下方列表。Table(4)表示位于結點4時的最短路徑情況,表示從結點0到4有兩條路徑,長度為3的路徑前驅為2;長度為4的路徑前驅為3。前驅括號里面第二個數表示對相同前驅結點的區分,如(4,1)、(4,2)。由列表可知,該字串的3-最短路徑結果集合為{5,5,6,6,7}。
當然,在實際情況中,權值不可能都設為1的,否則隨著字串長度n和最短路徑N的增大,長度相同的路徑數將會急劇增加。為了解決這樣的問題,我們需要通過某種策略為有向圖的邊賦權重,很自然的想法就是邊的權重就是該詞出現的可能性。
NShortPath的基本思想是Dijkstra算法的變種,拿1-最短路來說吧,先Dijkstra求一次最短路,然后沿著最短路的路徑走下去,只不過在走到某個節點的時候,檢查到該節點在路徑上的下一個節點是否還有別的路到它(從PreNode查),如果有,就走這些別的路中的沒走過第一條(它們都是最短路上的途徑節點)。然后推廣到N-最短路,N-最短路中PreNode有N個,分別對應n-最短路時候的PreNode,就這么簡單。
圖解
再談PreNode的準備
需要為每個頂點維護一個最小堆,最小堆里儲存的是邊的花費,每條邊的終點是這個頂點。還需要維護到每個頂點的前N個最小路徑的花費:
回憶一下Dijkstra求最短路的時候,我們只需記錄一個最短路的累計花費就行了
這與此處的N-最短路徑顯著不同。
在遍歷圖的時候,與Dijkstra最短路徑不同,N-最短路徑從第二個節點開始,需要將當前節點可能到達的邊根據累積第i短長度+該邊的長度之和排序記錄到PreNode隊列數組中,排序由CQueue完成的。
然后從CQueue出隊,這樣路徑長度就是升序了,按順序更新 weightArray[當前節點][第幾短路]就行了。
另外CQueue是一個不同于普通隊列的隊列,它維護了一個當前指針(下圖的藍色部分),這個藍色指針在求解第i短路徑的時候會用到。
假定看到這里,算法已經計算出了正確的PreNode隊列,下面討論如何從PreNode中找出N最短路徑的確切途經節點集合。
1-最短路徑的求解
整個計算過程維護了一個路徑棧,對于上圖來說,
1)首先將最后一個元素壓入棧(本例中是6號結點),什么時候這個元素彈出棧,什么時候整個任務結束。
2)對于每個結點的PreNode隊列,維護了一個當前指針,初始狀態都指向PreNode隊列中第一個元素。這個指針是由CQueue維護的,嚴格來講不屬于算法關心的問題。
3)從右向左依次取出PreNode隊列中的當前元素(當前元素出隊)并壓入棧,并將隊列指針重新指向隊列中第一個元素。如上圖:6號元素PreNode是3,3號元素PreNode是1,1號元素PreNode是0。
4)當第一個元素壓入棧后,輸出棧內容即為一條隊列。本例中0, 1, 3, 6便是一條最短路徑。
5)將棧中的內容依次彈出,每彈出一個元素,就將當時壓棧時該元素對應的PreNode隊列指針下移一格。如果到了末尾無法下移,則繼續執行第5步(也就是繼續出棧),如果仍然可以移動,則執行第3步。
對于本例,先將“0”彈出棧,在路徑上0的下一個是1,得出該元素對應的是1號“A”結點的PreNode隊列,該隊列的當前指針已經無法下移,因此繼續彈出棧中的“1” ;同理該元素對應3號“C”結點,因此將3號“C”結點對應的PreNode隊列指針下移。由于可以移動,因此將隊列中的2壓入隊列,2號“B”結點的PreNode是1,因此再壓入1,依次類推,直到0被壓入,此時又得到了一條最短路徑,那就是0,1,2,3,6。如下圖:
再往下,0、1、2都被彈出棧,3被彈出棧后,由于它對應的6號元素PreNode隊列記錄指針仍然可以下移,因此將5壓入堆棧并依次將其PreNode入棧,直到0被入棧。此時輸出第3條最短路徑:0, 1, 2, 4, 5, 6。如下圖:
輸出完成后,緊接著又是出棧,此時已經沒有任何棧元素對應的PreNode隊列指針可以下移,于是堆棧中的最后一個元素6也被彈出棧,此時輸出工作完全結束。我們得到了3條最短路徑,分別是:
0, 1, 3, 6,
0, 1, 2, 3, 6,
0, 1, 2, 4, 5, 6,
推廣到N-最短路
N-最短路中PreNode有N個,分別對應n-最短路時候的PreNode,也就是當前路徑是第n短的時候,當前節點對應的PreNode隊列。
在該圖中,觀察黃顏色的路徑長度表格,到達1號、2號、3號結點的路徑雖然有多條,但長度只有一種長度,但到達4號“D”結點的路徑長度有兩種,即長度可能是3也可能是4,此時在“最短路”處(index=0)記錄長度為3時的PreNode,在“次短路”處(index=1)處記錄長度為4時的PreNode,依此類推。
值得注意的是,此時用來記錄PreNode的坐標已經由前文求“1-最短路徑”時的一個數(ParentNode值)變為2個數(ParentNode值以及index值)。
如上圖所示,到達6號“末”結點的次短路徑有兩個ParentNode,一個是index=0中的4號結點,一個是index=1的5號結點,它們都使得總路徑長度為6。
當N=2時,我們求得了2-最短路徑,路徑長度有兩種,分別長度為5和6,而路徑總共有6條,如下:
最短路徑:
0, 1, 3, 6,
0, 1, 2, 3, 6,
0, 1, 2, 4, 5, 6,
========================
次短路徑
0, 1, 2, 4, 6,
0, 1, 3, 4, 5, 6,
0, 1, 2, 3, 4, 5, 6,
---------------------?
文章來源于random-walk的博客
 電子發燒友App
電子發燒友App















































評論