短波信道存在多徑時延、多普勒頻移和擴散、高斯白噪聲干擾等復雜現象。為了測試短波通信設備的性能,通常需要進行大量的外場實驗。相比之下,信道模擬器能夠在實驗室環境下進行類似的性能測試,而且測試費用少、可重復性強,可以縮短設備的研制周期。所以自行研制信道模擬器十分必要。
信道模擬器可選用比較有代表性的 Watterson 信道模型 ( 即高斯散射增益抽頭延遲線模型 ) ,其中一個重要環節就是快速產生高斯白噪聲序列,便于在添加多普勒擴展和高斯白噪聲影響時使用。傳統的高斯白噪聲發生器是在微處理器和 DSP 軟件系統上實現的,其仿真速度比硬件仿真器慢的多。因此,選取 FPGA 硬件平臺設計高斯白噪聲發生器可以實現全數字化處理,同時測試費用少、可重復性強、實時性好、速度快,能較好地滿足實驗需求。
本文提出了一種基于 FPGA 的高斯白噪聲序列的快速產生方案。該方案根據均勻分布和高斯分布之間的映射關系,采用適合在 FPGA 中實現的折線逼近法。該方法實現簡單,快速且占用的硬件資源少,而且采用 VHDL 語言編寫,可移植性強,并可靈活地嵌入調制解調器中使用。
1 均勻分布隨機數發生
1.1 m 序列發生器
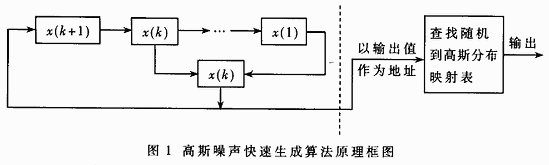
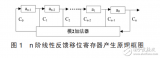
偽隨機噪聲具有類似隨機噪聲的一些統計特性,且便于重復產生和處理,因此獲得了廣泛的應用。 m 序列就是一種常用的偽隨機序列,該序列又被稱作最長線性反饋移存序列。 m 序列是由線性反饋移位寄存器產生的周期最長的一種序列。如果選用 n 級線性反饋移位寄存器,則 m 序列的周期為 (2n-1) 。對于 m 序列來說,將 n 級線性反饋移位寄存器狀態看成無符號整數,則狀態的取值范圍為 1 ~ (2n-1) ,并且在 m 序列的一個周期內,移位寄存器的每種狀態都會出現且只出現一次,但要注意線性反饋移位寄存器的初始狀態設定為非零值,并且在給定任意非零初始狀態時, m 序列的周期都不變。顯然,移位寄存器的狀態值是服從均勻分布隨機數。制作 m 序列發生器時,線性反饋移位寄存器的反饋線連接情況可通過查找本原多項式來得到 ( 系數為 1 表示對應位有反饋線連接,為 0 表示對應位無反饋線連接 ) 。所以,線性反饋移位寄存器反饋線的數目以及模 2 加法器的數目直接決定于本原多項式的項數。為降低硬件資源的消耗,設計時可選取項數少的本原多項式。為了使偽隨機序列的周期足夠長以滿足設計要求,采用的本原多項式為: x18+x7+1 ,即用一個 18 級線性反饋移位寄存器就可產生周期為 (218-1) 的 m 序列。其連線如圖 1 所示。
1.2 降低相關性模塊 高斯白噪聲信號是一個隨機過程,每個樣值點都是一個高斯變量,其雙邊功率譜密度為常數 N0 / 2 ,即:
由 (2) 式可見,高斯白噪聲在任意兩個不同時刻的采樣信號是統計獨立的。但是,從 m 序列的產生過程可見,每個時鐘周期中,線性反饋移位寄存器只移出一個最高位,并反饋一個值給最低位,所以,相鄰的幾個狀態之間不是完全獨立的。這必然影響高斯白噪聲任意兩個不同時刻采樣信號之間的獨立性。所以要進行非相關性操作。為了減小相關性,通常的方法是產生高斯序列后再接一個交織器,把高斯序列出現的前后順序打亂。但建交織器要占用 FPGA 的硬件資源,所以,本設計不采用交織器。
考慮到 m 序列的周期為 (2n-1) ,第 2n 個值往后都是不斷重復第 1 個到第 (2n-1) 個狀態。所以只要線性反饋移位寄存器每隔 r 個同步時鐘 ( 其中 r=2i , i 為整數 ) 輸出一個狀態值 ( 即線性反饋移位寄存器每變換 r 個狀態輸出一次狀態值 ) ,就能在不改變 m 序列原有周期的情況下減小相關性,且不增加硬件資源的消耗。但要注意: r 一定要是 2 的冪,這樣才能保證 m 序列的周期不變。2 均勻分布向高斯分布的轉換
2.1 均勻分布和高斯分布之間的映射關系 設 X 服從 [1 , 218-1] 區間內的均勻分布; Y 服從均值為 0 、方差為 1 的標準正態分布,那么,考慮到高斯分布的實際情況, Y 僅在 [-4 , 4] 之間取值即可。 Y 的概率密度函數為:

2.2 折線逼近法
如果直接應用上述映射關系進行均勻分布向高斯分布的轉換,則需開辟 (218-1) 個物理空間來建立查找表,這幾乎不可能實現。但由圖 2 可見,其關系曲線在很大區間上表現出線性關系,所以,可以以斜率不同的直線段分段逼近關系曲線。在一定精度要求下,該方法簡單易行,占用硬件資源少,適合在 FPGA 中實現,從而實現由服從均勻分布向服從高斯分布的快速轉換。圖 3 是關系曲線 ( 實線 ) 和 15 段折線逼近法 ( 虛線 ) 的擬合圖,由圖可見,其實線和虛線擬合得很好,從而證明了折線逼近法能較好的反映映射關系。
利用 m 序列的周期特性可降低高斯白噪聲任意兩個不同時刻的采樣信號的相關性。在線性反饋移位寄存器中每隔 r 個同步時鐘 ( 其中 r=2i , i 為整數 ) 輸出一個狀態值作為均勻分布的隨機數輸入可實現均勻分布向高斯分布的轉化。為了選擇合適的 r 值,圖 4 分別給出了 r 為 0 、 2 、 8 時所生成的 10000 點高斯序列的功率譜。由圖 4 可見, r=8 時的功率譜基本水平,即系統產生的高斯白噪聲任意兩個不同時刻的采樣信號可看成統計獨立的,這與理論上對高斯白噪聲的定義相一致。同時也證明了降低相關性模塊是可行和有效的。


3 硬件實現
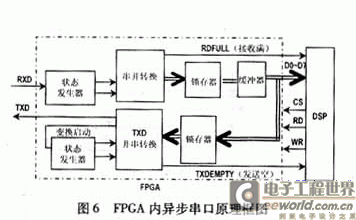
在 ISE8.1i 開發環境中使用 VHDL 語言可實現上述高斯白噪聲發生器的功能。本設計選用 Xilinx 的 xc3s1200e-4fg320 作為目標器件。其硬件實現框圖如圖 5 所示。
產生高斯白噪聲先后通過兩個模塊來實現。一是均勻隨機數發生模塊;二是均勻分布向高斯分布轉化模塊。其中均勻隨機數發生模塊包括 m 序列發生器和非相關化處理 ( 降低相關性操作 ) ;均勻分布向高斯分布轉化模塊包括比較選擇器、相應的延時操作以及算術計算模塊。

在 ISE8.1i 開發環境中得到的系統功能仿真圖如圖 6 所示。實驗中,系統的輸入時鐘為 60MHz 。圖 6 中的 regl_value 表示線性反饋的移位寄存器在時鐘 clk1 上升沿觸發的狀態值。 reg2_value 表示在同步時鐘 clk2 上升沿采樣 reg_value1 的值, clk2 是 clk1 的 8 倍分頻。仿真證明,本系統可以實現線性反饋移位寄存器每轉 8 次取出一個狀態值,并可減小不同時刻隨機變量之間的相關性 ( 非相關化處理 ) 。根據 reg2_value 并通過比較選擇器輸出對應直線段的 slope( 斜率 ) 、 point( 起點的橫坐標 ) 、 point_value( 起點的縱坐標 ) 可見, reg2_value_delay 比 reg2_value 可延時半個 clk2 ,因而可保證輸入算術計算模塊的數據的同步。這樣,再經算式: gauss_output=(reg2_value_delay-point)*slope+point_value ,就可得到高斯白噪聲序列。為了確保采得穩定的信號值,操作時應在信號持續時間的中間位置進行采樣。由于高斯白噪聲序列 gauss_output 是 reg2_value_delay ,、 point 、 slope 、 point_value 之間的加、減、乘運算所得到的,所以, gauss_output 有相應延時。
本設計用 Xilinx 的 xc3s1200e-4fg320 為目標器件來對代碼進行綜合,所用的 FPGA 資源如下:

可見,該方案占用硬件資源較少。
為了驗證硬件實現的正確性,還可將其下載到開發板,并采用 ChipScope Pro 8.1i 將硬件產生的高斯白噪聲序列通過并口回傳,同時將數據導入到 Matlab 。由于 ChipScope 要利用 FPGA 的片內存儲空間暫存采樣值,所以,一次采集的信號數目有限且與 FPGA 型號有關。筆者將一次采集到的 16384 個樣值導入 Maflab 后,再將數據小數化 ( 因為 FPGA 中處理的是定點數 ) ,然后調用 Matlab 中的 psd 函數估計出了其功率譜圖。實際結果證明,本系統產生的高斯白噪聲與理論值非常接近,也就是說,該方案可行。
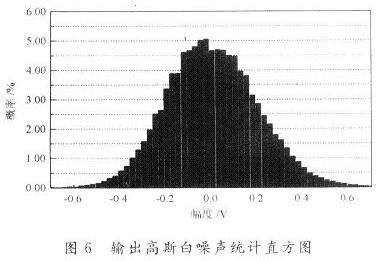
由于本系統采用 VHDL 語言編寫,故其可移植性較強。當在通信工程中需要帶限高斯白噪聲時,就可在高斯白噪聲后接一個帶通濾波器 ( 在 FPGA 中應用自帶 IP 核可輕松實現 ) 。由于濾波后的噪聲能量會有損失,所以要做相應的能量補償。之后,再將產生的帶限高斯白噪聲序列 ( 約 50000 點 ) 導入 Matlab 中,然后調用 hist 函數就可得到圖 7 所示的序列直方圖,而調用 psd 函數即可得到圖 8 所示的序列功率譜圖。從直方圖可見帶限高斯白噪聲的概率密度函數是高斯型的,而從功率譜可見,在通帶內,功率譜密度近似為常數,這些都與理論一致。

4 結束語
本文提出了一種在 FPGA 中快速產生高斯白噪聲序列的實現方案。同時基于均勻分布和高斯分布之間的映射關系曲線,提出并應用了適合在 FPGA 中實現的折線逼近法。本文采用了 15 條首尾連接的直線段去逼近映射關系曲線 ( 按不同的工程精度要求,可選擇個數不同的直線段去逼近 ) 。顯然,所用的折線拐角越多 ( 直線段個數越多 ) ,精度越高,但所消耗的 FPGA 資源也越多。該方案具有簡單易行,運算量小等優點。而且實現速度快,可源源不斷的產生高斯白噪聲序列,同時占用的硬件資源較少。由于軟件采用 VHDL 語言編寫,可移植性強,故可靈活用于 Watterson 信道模擬器或嵌入調制解調器等其它系統。
 電子發燒友App
電子發燒友App










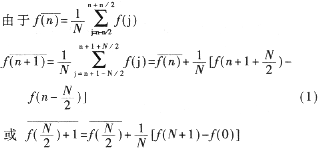













評論