無人駕駛路徑規劃

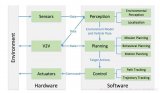
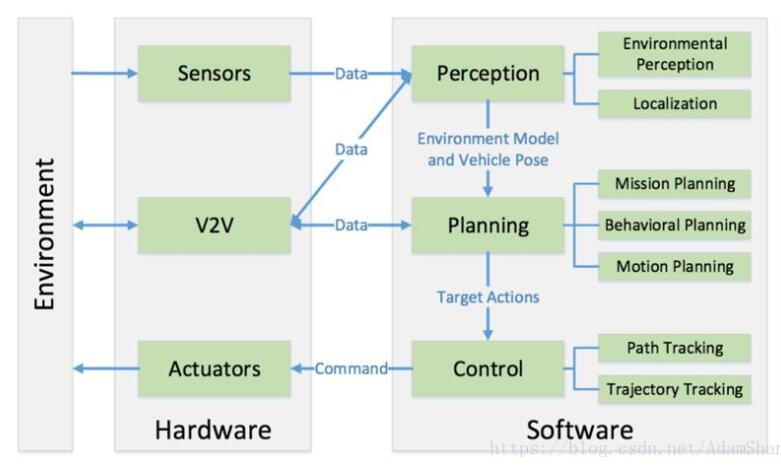
眾所周知，無人駕駛大致可以分為三個方面的工作：感知，決策及控制。 路徑規劃是感知和控制之間的決策階段，主要目的是考慮到車輛動力學、機動能力以及相應規則和道路邊界條件下，為車輛提供通往目的地的安全和無碰撞的路徑。 路徑規劃問題可以分為兩個方面： （一）全局路徑規劃：全局路徑規劃算法屬于靜態規劃算法，根據已有的地圖信息（SLAM）為基礎進行路徑規劃，尋找一條從起點到目標點的最優路徑。 通常全局路徑規劃的實現包括Dijikstra算法，A*算法，RRT算法等經典算法，也包括蟻群算法、遺傳算法等智能算法； （二）局部路徑規劃：局部路徑規劃屬于動態規劃算法，是無人駕駛汽車根據自身傳感器感知周圍環境，規劃處一條車輛安全行駛所需的路線，常應用于超車，避障等情景。通常局部路徑規劃的實現包括動態窗口算法（DWA），人工勢場算法，貝塞爾曲線算法等，也有學者提出神經網絡等智能算法。

全局路徑規劃 - RRT算法原理

RRT算法，即快速隨機樹算法（Rapid Random Tree），是LaValle在1998年首次提出的一種高效的路徑規劃算法。RRT算法以初始的一個根節點，通過隨機采樣的方法在空間搜索，然后添加一個又一個的葉節點來不斷擴展隨機樹。 當目標點進入隨機樹里面后，隨機樹擴展立即停止，此時能找到一條從起始點到目標點的路徑。算法的計算過程如下： step1：初始化隨機樹。將環境中起點作為隨機樹搜索的起點，此時樹中只包含一個節點即根節點；? stpe2：在環境中隨機采樣。在環境中隨機產生一個點，若該點不在障礙物范圍內則計算隨機樹中所有節點到的歐式距離，并找到距離最近的節點，若在障礙物范圍內則重新生成并重復該過程直至找到;?? stpe3：生成新節點。在和連線方向，由指向固定生長距離生成一個新的節點，并判斷該節點是否在障礙物范圍內，若不在障礙物范圍內則將添加到隨機樹 中，否則的話返回step2重新對環境進行隨機采樣； step4：停止搜索。當和目標點之間的距離小于設定的閾值時，則代表隨機樹已經到達了目標點，將作為最后一個路徑節點加入到隨機樹中，算法結束并得到所規劃的路徑。 RRT算法由于其隨機采樣及概率完備性的特點，使得其具有如下優勢： （1）不需要對環境具體建模，有很強空間搜索能力； （2）路徑規劃速度快； （3）可以很好解決復雜環境下的路徑規劃問題。 但同樣是因為隨機性，RRT算法也存在很多不足的方面： （1）隨機性強，搜索沒有目標性，冗余點多，且每次規劃產生的路徑都不一樣，均不一是最優路徑； （2）可能出現計算復雜、所需的時間過長、易于陷入死區的問題； （3）由于樹的擴展是節點之間相連，使得最終生成的路徑不平滑； （4）不適合動態環境，當環境中出現動態障礙物時，RRT算法無法進行有效的檢測； （5）對于狹長地形，可能無法規劃出路徑。

RRT算法Matlab實現

使用matlab2019來編寫RRT算法，下面將貼出部分代碼進行解釋。

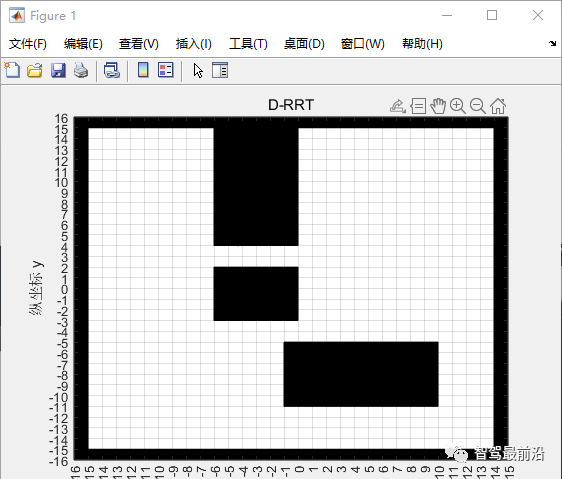
1、生成障礙物 在matlab中模擬柵格地圖環境，自定義障礙物位置。

%% 生成障礙物
ob1 = [0,-10,10,5]; ? ? ? ? ? ? % 三個矩形障礙物
ob2 = [-5,5,5,10];
ob3 = [-5,-2,5,4];


ob_limit_1 = [-15,-15,0,31]; ? ?% 邊界障礙物
ob_limit_2 = [-15,-15,30,0];
ob_limit_3 = [15,-15,0,31];
ob_limit_4 = [-15,16,30,0];


ob = [ob1;ob2;ob3;ob_limit_1;ob_limit_2;ob_limit_3;ob_limit_4]; ?% 放到一個數組中統一管理


x_left_limit = -16; ? ? ? ? ? ? % 地圖的邊界
x_right_limit = 15;
y_left_limit = -16;
y_right_limit = 16;

?

我在這隨便選擇生成三個矩形的障礙物，并統一放在ob數組中管理，同時定義地圖的邊界。

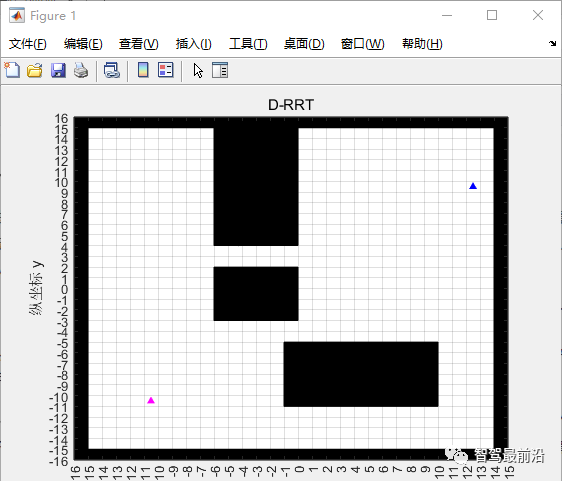
2、初始化參數設置 初始化障礙物膨脹范圍、地圖分辨率，機器人半徑、起始點、目標點、生長距離和目標點搜索閾值。

%% 初始化參數設置
extend_area = 0.2; ? ? ? ?% 膨脹范圍
resolution = 1; ? ? ? ? ? % 分辨率
robot_radius = 0.2; ? ? ? % 機器人半徑


goal = [-10, -10]; ? ? ? ?% 目標點
x_start = [13, 10]; ? ? ? % 起點


grow_distance = 1; ? ? ? ?% 生長距離
goal_radius = 1.5; ? ? ? ?% 在目標點為圓心，1.5m內就停止搜索

? 3、初始化隨機樹 初始化隨機樹，定義樹結構體tree以保存新節點及其父節點，便于后續從目標點回推規劃的路徑。

%% 初始化隨機樹
tree.child = []; ? ? ? ? ? ? ? % 定義樹結構體，保存新節點及其父節點
tree.parent = [];
tree.child = x_start; ? ? ? ? ?% 起點作為第一個節點
flag = 1; ? ? ? ? ? ? ? ? ? ? ?% 標志位
new_node_x = x_start(1,1); ? ? % 將起點作為第一個生成點
new_node_y = x_start(1,2);
new_node = [new_node_x, new_node_y];

4、主函數部分 主函數中首先生成隨機點，并判斷是否在地圖范圍內，若超出范圍則將標志位置為0。

rd_x = 30 * rand() - 15; ? ?% 生成隨機點
rd_y = 30 * rand() - 15; ? ?
if (rd_x >= x_right_limit || rd_x <= x_left_limit ||... % 判斷隨機點是否在地圖邊界范圍內
 ? ?rd_y >= y_right_limit || rd_y <= y_left_limit)
 ? ?flag = 0;
end

調用函數cal_distance計算tree中距離隨機點最近的節點的索引，并計算該節點與隨機點連線和x正向的夾角。

[angle, min_idx] = cal_distance(rd_x, rd_y, tree); ? ?% 返回tree中最短距離節點索引及對應的和x正向夾角

cal_distance函數定義如下：

function [angle, min_idx] = cal_distance(rd_x, rd_y, tree)
 ? ?distance = [];
 ? ?i = 1;
 ? ?while i<=size(tree.child,1)
 ? ? ? ?dx = rd_x - tree.child(i,1);
 ? ? ? ?dy = rd_y - tree.child(i,2);
 ? ? ? ?d = sqrt(dx^2 + dy^2);
 ? ? ? ?distance(i) = d;
 ? ? ? ?i = i+1;
 ? ?end
 ? ?[~, min_idx] = min(distance);
 ? ?angle = atan2(rd_y - tree.child(min_idx,2),rd_x - tree.child(min_idx,1));
end

隨后生成新節點。

new_node_x = tree.child(min_idx,1)+grow_distance*cos(angle);% 生成新的節點
new_node_y = tree.child(min_idx,2)+grow_distance*sin(angle);
new_node = [new_node_x, new_node_y];

接下來需要對該節點進行判斷： ① 新節點是否在障礙物范圍內； ② ?新節點和父節點的連線線段是否和障礙物有重合部分。 若任意一點不滿足，則將標志位置為0。實際上可以將兩個判斷結合，即判斷新節點和父節點的連線線段上的點是否在障礙物范圍內。

for k=1:1:size(ob,1) 
 ? ?for i=min(tree.child(min_idx,1),new_node_x):0.01:max(tree.child(min_idx,1),new_node_x) ? ?% 判斷生長之后路徑與障礙物有無交叉部分
 ? ? ? ?j = (tree.child(min_idx,2) - new_node_y)/(tree.child(min_idx,1) - new_node_x) *(i - new_node_x) + new_node_y;
 ? ? ? ?if(i >=ob(k,1)-resolution && i <= ob(k,1)+ob(k,3) && j >= ob(k,2)-resolution && j <= ob(k,2)+ob(k,4))
 ? ? ? ? ? ?flag = 0;
 ? ? ? ? ? ?break
 ? ? ? ?end
 ? ?end
end

?

在這我采用的方法是寫出新節點和父節點連線的直線方程，然后將x變化范圍限制在min(tree.child(min_idx,1),new_node_x)max(tree.child(min_idx,1),new_node_x)內，0.01即坐標變換的步長，步長越小判斷的越精確，但同時會增加計算量；

步長越大計算速度快但是很可能出現誤判，如下圖所式。 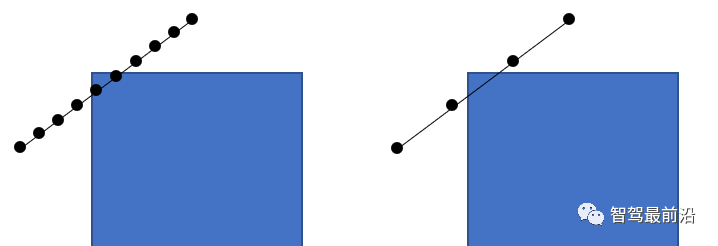左圖：合適的步長 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? 右圖：步長過大 判斷標志位若為1，則可以將該新節點加入到tree中，注意保存新節點和它的父節點，同時顯示在figure中，之后重置標志位。

if (flag == true) ? ? ? ? ? % 若標志位為1，則可以將該新節點加入tree中
 ? ?tree.child(end+1,:) = new_node;
 ? ?tree.parent(end+1,:) = [tree.child(min_idx,1), tree.child(min_idx,2)];
 ? ?plot(rd_x, rd_y, '.r');hold on
 ? ?plot(new_node_x, new_node_y,'.g');hold on
 ? ?plot([tree.child(min_idx,1),new_node_x], [tree.child(min_idx,2),new_node_y],'-b');
end
 ? ?
flag = 1; ? ? ? ? ? ? ? ? ? % 標志位歸位

最后就是把障礙物、起點終點等顯示在figure中，并判斷新節點到目標點距離。若小于閾值則停止搜索，并將目標點加入到node中，否則重復該過程直至找到目標點。

%% 顯示
for i=1:1:size(ob,1) ? ? ? ?% 繪制障礙物
 ? ?fill([ob(i,1)-resolution, ob(i,1)+ob(i,3),ob(i,1)+ob(i,3),ob(i,1)-resolution],...
 ? ? ? ? [ob(i,2)-resolution,ob(i,2)-resolution,ob(i,2)+ob(i,4),ob(i,2)+ob(i,4)],'k');
end
hold on


plot(x_start(1,1)-0.5*resolution, x_start(1,2)-0.5*resolution,'b^','MarkerFaceColor','b','MarkerSize',4*resolution); % 起點
plot(goal(1,1)-0.5*resolution, goal(1,2)-0.5*resolution,'m^','MarkerFaceColor','m','MarkerSize',4*resolution); % 終點
set(gca,'XLim',[x_left_limit x_right_limit]); % X軸的數據顯示范圍
set(gca,'XTick',[x_left_limitx_right_limit]); % 設置要顯示坐標刻度
set(gca,'YLim',[y_left_limit y_right_limit]); % Y軸的數據顯示范圍
set(gca,'YTick',[y_left_limity_right_limit]); % 設置要顯示坐標刻度
grid on
title('D-RRT');
xlabel('橫坐標 x'); 
ylabel('縱坐標 y');
pause(0.05);
if (sqrt((new_node_x - goal(1,1))^2 + (new_node_y- goal(1,2))^2) <= goal_radius) % 若新節點到目標點距離小于閾值，則停止搜索，并將目標點加入到node中
 ? ?tree.child(end+1,:) = goal; ? ? ? ? % 把終點加入到樹中
 ? ?tree.parent(end+1,:) = new_node;
 ? ?disp('find goal!');
 ? ?break
end

5、繪制最優路徑 從目標點開始，依次根據節點及父節點回推規劃的路徑直至起點，要注意tree結構體中parent的長度比child要小1。最后將規劃的路徑顯示在figure中。

%% 繪制最優路徑
temp = tree.parent(end,:);
trajectory = [tree.child(end,1)-0.5*resolution, tree.child(end,2)-0.5*resolution];
for i=size(tree.child,1):-1:2
 ? ?if(size(tree.child(i,:),2) ~= 0 & tree.child(i,:) == temp)
 ? ? ? ?temp = tree.parent(i-1,:);
 ? ? ? ?trajectory(end+1,:) = tree.child(i,:);
 ? ?if(temp == x_start)
 ? ? ? ?trajectory(end+1,:) = [temp(1,1) - 0.5*resolution, temp(1,2) - 0.5*resolution];
 ? ?end
 ? ?end
end
plot(trajectory(:,1), trajectory(:,2), '-r','LineWidth',2);
pause(2);

程序運行最終效果如下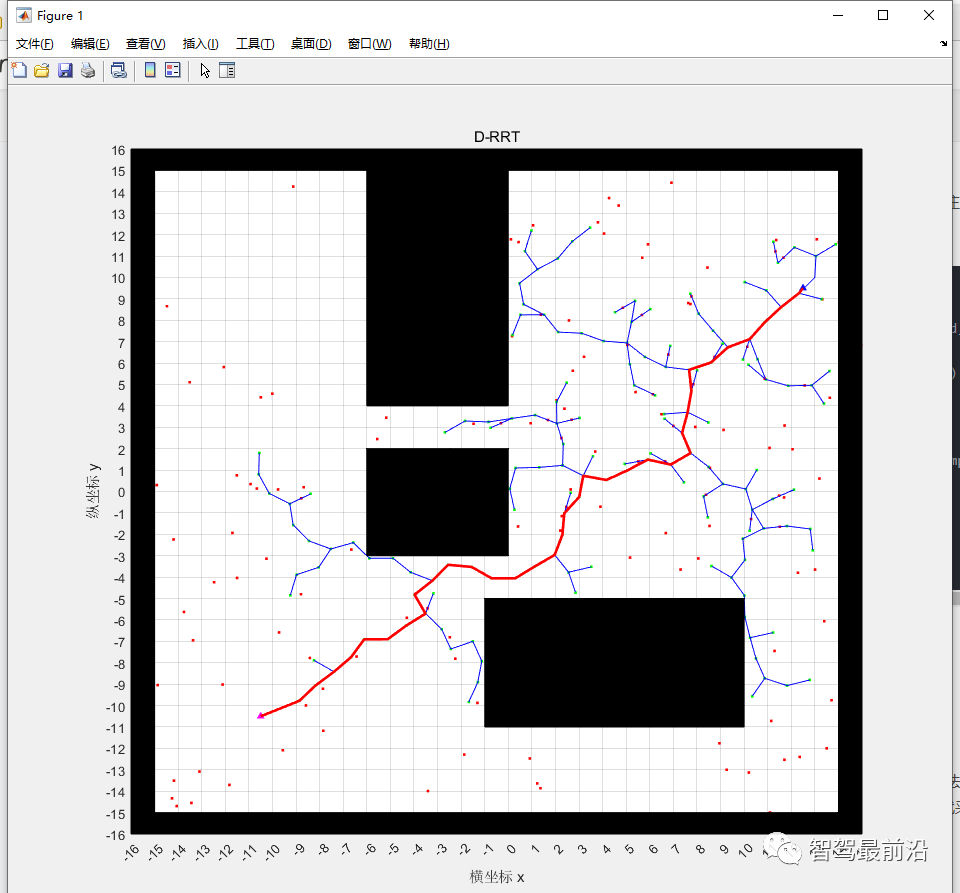： ?紅點都是生成點隨機點，綠點是tree中節點，紅色路徑即為RRT算法規劃的路徑。 6、路徑平滑（B樣條曲線） 由于規劃的路徑都是線段連接，在節點處路徑不平滑，這也是RRT算法的弊端之一。一般來說軌跡平滑的方法有很多種，類似于貝塞爾曲線，B樣條曲線等。 我在這采用B樣條曲線對規劃的路徑進行平滑處理，具體的方法和原理我后續有時間再進行說明，這里先給出結果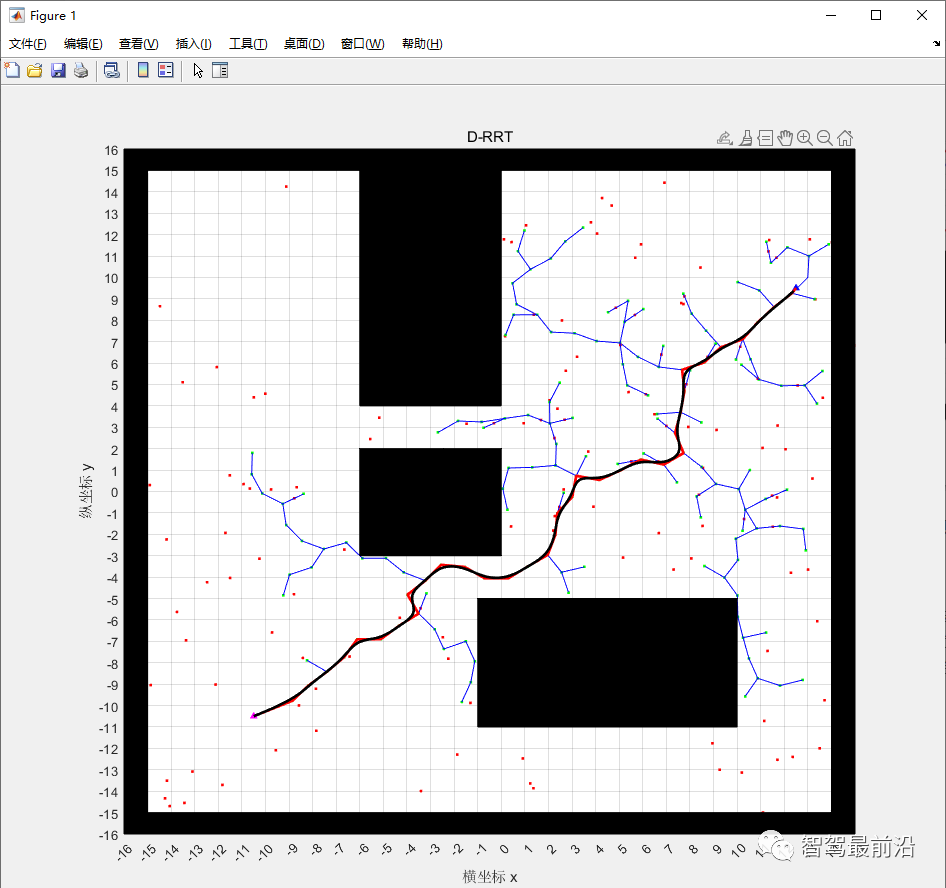： ?黑色曲線即位平滑處理后的路徑。 多組結果對比 ① 相鄰兩次仿真結果對比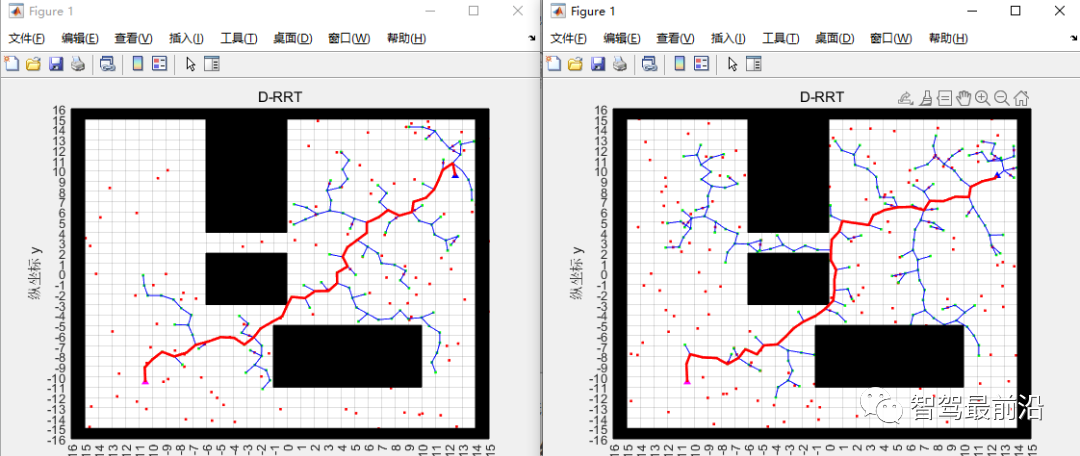： 可以看出由于隨機采樣的原因，任意兩次規劃的路徑都是不一樣的。? ② 復雜環境下的路徑規劃。選取一個相對復雜的環境，仿真結果如下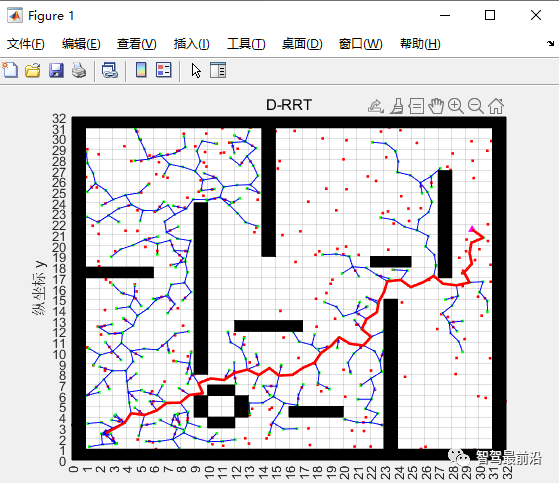： 可以看出RRT算法可以很好解決復雜環境下的路徑規劃問題。 ③ 狹窄通道下的路徑規劃。選取一個狹窄通道環境，仿真結果如下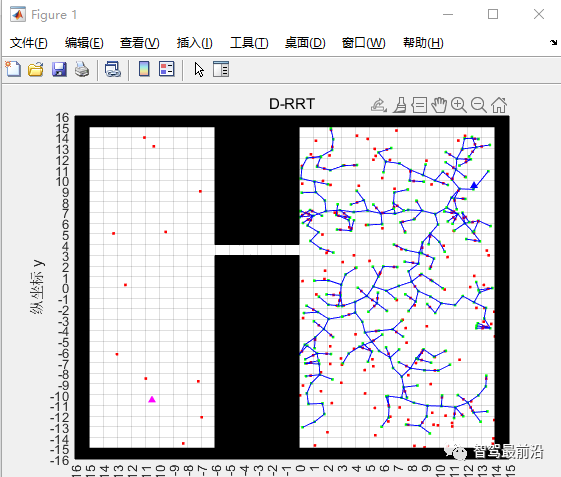： 由于環境采樣的隨機性，在狹長通道內生成隨機點的概率相對較低，導致可能無法規劃出路徑。

編輯：黃飛

?