我們解決了算法公平性的問題:確保分類器的結果不會偏向于敏感的變量值，比如年齡、種族或性別。由于一般的公平性度量可以表示為變量之間(條件)獨立性的度量，我們提出使用Renyi最大相關系數將公平性度量推廣到連續變量。我們利用Witsenhausen關于Renyi相關系數的角色塑造，提出了一個鏈接到f-區別的可微實現。這使得我們可以通過使用一個限制這個系數上限的懲罰，將公平意識學習推廣到連續變量學習。這些理論允許公平擴展到變量，如混合種族群體或沒有閾值效應的金融社會地位。這種懲罰可以通過允許使用深度網絡的小批量生產來估計。實驗結果表明，二進制變量的最新研究成果令人滿意，并證明了保護連續變量的能力。

1. 介紹

隨著人工智能工具在社會中的普及，確保敏感信息(例如個人的種族群體知識)不會“不公平地”影響學習算法的結果，正受到越來越多的關注。為了實現這一目標，正如在相關工作3.1節中詳細討論的那樣，有三類方法: 首先修改一個預先訓練的分類器，同時最小化對性能的影響(Hardt等人，2016;Pleiss等人，2017)，其次在訓練期間執行公平性，可能以凸性為代價(Zafar等人，2017)；第三，修改數據表示并使用經典算法(Zemel 等人， 2013;Doninietal等人，2018)。正如(Hardt 等人, 2016) 所闡述的，算法公平性的核心要素是在兩個精心選擇的隨機變量之間估計和保證(條件)獨立性的能力--通常涉及由算法作出的決定和保護的變量以及“積極的”結果。在接下來的介紹中，我們將把這兩個隨機變量稱為u和v。雖然在一般情況下u和v可以是連續變量——例如預測概率或時間等變量——但迄今為止，公平方面的大部分工作都集中在保護分類變量上。本文中，我們放松了這種假設。

從應用的角度來看，這是可取的，因為它避免了考慮將連續值作為預先確定的，在學習模型中呈現閾值效應的“分類箱”。當考慮到年齡、種族比例或性別流動性測量時，這些閾值沒有實際意義。此外，一種描述公平性約束的平滑和連續的方法——一種同時考慮元素順序(例如10yo<11yo)的方法——也很重要。作為一個來自現實世界的例子，(Daniels等人，2000)指出財務狀況是醫療保健的一個敏感變量。

從統計學的觀點來看，考慮到u和v之間的相關性可以是任意復雜的，相關性的度量是具有挑戰性的。在譜的一側（有經驗的一側）引入了簡單易行的相關系數，如皮爾遜相關系數、斯皮爾曼秩相關系數和肯德爾相關系數。可悲的是，盡管這樣的相關系數能夠證明獨立性是錯誤的，但它們無法證明獨立性。他們只是表達了獨立的必要條件。另一方面，理論上的單地平線(Gebelein，1941)引入了hirschfeld-Gebelein-Renyi最大相關系數(HGR)，該系數在估值為零時具有證明獨立性的理想性質(Renyi，1959)，但在一般情況下難以計算。然而，HGR是一種以[0,1]為參數的相關性度量，它獨立于u和v的邊緣，允許監管者以一個絕對閾值作為公平標準使用它。

我們的首要目標是利用算法公平獨立性的測量。同時，深度學習的興起和可微編程的思想主張利用具有良好的一階行為和有限的計算成本的可微近似來懲罰神經網絡。在這項工作中，我們推導了一個可微的非參數估計，基于Witsenhausen的角色塑造KDE的結合。我們證明了這個估計的經驗性能，并且我們緊緊地用一個f-區分的量給它上界。只要兩個隨機變量(u或v)中的一個是二值的，就可以得到所提出的界。注意，聯合分布與其邊際乘積之間的f-發散在可逆映射的作用下是不變的(Nelsen，2010)，并且可以用作相依性的度量。

作為第二個貢獻，我們證明了我們關于HGR系數的上界可以用來懲罰一個模型的學習。它甚至在經驗上被證明在小批量估計時表現良好，允許它與隨機梯度訓練的神經網絡結合使用。另一個關鍵區別是，我們能夠處理連續的敏感變量。我們的方法也擴展了Kamishima等人(2011)的工作，他們提出使用互信息(MI)的估計作為懲罰，但他們的估計方法僅限于分類變量。此外，即使將MI推廣到連續情形，我們也證明了我們的正則化程序既能得到更好的模型，又能降低對超參數值的敏感性。

本文的其余部分組織如下:首先，我們明確了獨立性測度和不同公平標準之間的聯系，如不同的影響和平等的賠率。其次，介紹了我們提出的能夠處理連續變量的HGR近似，并利用它對算法公平性的損失進行正則化。我們跟著一個實驗部分，我們經驗證明，我們的近似是競爭狀態的依賴性估計和算法公平性，當明智的屬性是分類的，并且最小化可以使用小批量的數據，如果數據集足夠大了。最后，我們證明了我們的方法適用于連續的敏感屬性。

2. HGR作為一種公平標準

2.1公平標準概述

許多關于公平的概念目前正在調查中，但是對于哪些概念是最合適的還沒有達成共識(Hardt等人，2016;Zafar等人，2017;Dwork等人，2012)。事實上，這是一個選擇，不僅需要統計學和因果論證，還需要倫理學的論證。這些指標之間的一個共同線索是依賴于統計獨立性。公平性遇到機器學習時試圖根據一些可用信息x(例如:信用卡歷史)對某個變量y(例如:默認付款)建立一個預測y’;這個預測可能對某個敏感屬性z(例如:性別)有偏見或不公平。

最初提出的衡量公平性的概念是預測人口平等，即P(Y=1|Z=1)=P(Y=1|Z=0)，它被不同影響的標準所測量(Feldman et al., 2015)：

?

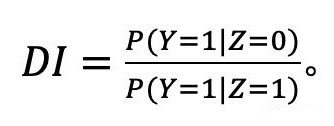
這個標準甚至是美國平等就業機會委員會建議(eeoc.1979)的一部分，該建議主張它不應該低于0.8——也被稱為80%規則。雖然最初定義的二元變量，人口平價可以很容易地推廣到Y⊥Z需求，即使Z非二進制。

人口統計平價被批評因為忽略了可能解釋Y和Z之間數據已經存在的相關性的混淆變量。比如，一個模型隨機選擇10%的男性，然后選擇最好的10%的女性，這將是完全公平的w.r.t.DI。為了部分地克服這些限制，平衡賠率被引入(Zafar等人，2017;Hardt等人，2016)作為衡量方法，P(Y=1|Z=1，Y=y)=P(Y=1|Z=0,Y=y)。僅y=1的特定情況被稱為EO，并且通常通過EO的差異來測量：DEO= P(Y=1|Z=1，Y=1)-P(Y=1|Z=0,Y=1)

同樣，與人口平等相似，平等機會可以通過獨立概念等效地表示。已經存在一些其他公平的概念了，比如試圖確保預測Y對于受保護屬性的精確度不會高于另一組的標準。盡管人們投入了大量精力尋找新的公平定義，以涵蓋各種可能的社會偏見，但相關的統計措施仍然局限于Y和Z的二進制值。

3. 公平意識學習

在前面的章節中，我們主張使用HGR來推導公平性評價標準。那么這種方法是否可以用來推導懲罰方案，以便在學習階段加強公平性。為了避免繁瑣的表示法和討論，我們將重點放在均衡賠率設置上，但是對于其他的公平性設置，我們可以推導出類似的學習方案。特別是，我們在附錄中提供了一套相應的實驗用于設定人口平價。

3.1最新研究

隨著機器學習成為保險公司、健康系統、法律等方面一種常見的工具，學習公平模型是一個越來越受關注的話題。目前，研究集中于二進制例子。在這樣的設定下可以基于Z和Y校準預測Y的模型的后驗，以便例如滿足DEO約束，代價是通過重新加權由模型輸出的概率或適應分類器閾值而失去一些精度。為了在學習過程中嵌入公平性，可能在準確性和公平性之間找到比后驗可以實現的更好的權衡，有人在學習時整合了重新加權，并提出了一種對成本敏感的公平分類方法。然而，這些方法與感興趣的變量的二元性質密切相關。

另一種方法是在學習時給優化個體添加公平約束。目前有兩種約束。第一種的均衡倍率的簡化實例化的方法是將條件分布π 約束為任何y，在分布之間提供一些距離D。這個想法被推廣到Y函數的期望之間的距離，其允許使用條件分布的更高矩。第二類的思想與我們的方法相關。KL使用了f-區分，但是懲罰評估對二進制例子是特定的。最后Zafar等人提出了一種旨在Y和Z之間的條件協方差的約束，僅相對應于去除線性相關，而HGR可以解決更復雜的情況。當目標為在神經網絡上使用該懲罰時最后一點尤為重要，它只考慮線性依賴有絕對能力擬合懲罰。

最后，有一系列的工作旨在提出回歸公平的測量方法。它們使用協方差或者更為少見的度量標準（如Gini）。這些依賴于線性系統的屬性—可能在內核空間—我們正則化深度網絡和不限制人口平等。

4. 實驗

為了從經驗上支持前面提出的不同主張，我們提供了幾個實驗。我們首先證明了當檢驗實值變量的獨立性時，我們的HGR近似值與RDC(Lopez-Paz等人，2013)是有競爭性的。其次，在訓練一個公平的分類器的背景下——比如，我們希望一個分類器的二進制結果是w.r.t公平。一個二進制特征z——我們檢查我們的近似可以被用來規范一個分類器，以增強公平性，其結果與現有的技術水平相當。此處我們發現，當數據集有幾千個數據點時，我們可以確保其估計的正分類概率的公平性。最后，我們證明了我們可以保護一個連續敏感屬性的w.r.t.分類器的輸出。

4.1 基于KDE的Witsenhausen的角色塑造

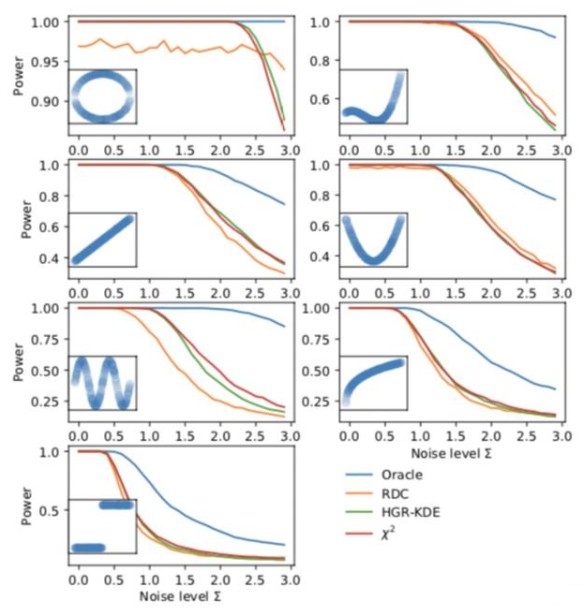
我們首先復現了RDC。依賴度量的力量被定義為區分具有相同邊緣形式的獨立樣本和未確定樣本的能力，并以概率的形式表示。在這里，我們將HGR-KDE估計與作為非線性相關度量的RDC進行比較。我們復制了7個雙變量關聯模式，如圖1所示。對于每個聯結模式F，n=500樣本的500次生成，其中我們從X～unif[0，1]中取樣得到(xi，F(xi))元組。接下來，我們獨立于Y～unif[0，1]重新生成輸入變量，以生成每個樣本具有相等邊緣的獨立版本(Y,F(X))。圖1顯示了當某些零平均高斯加性噪聲的標準差從0增加到3時，討論的非線性脫離度量的功率。我們觀察到χ2與HGR-KDE估計非常相似，但在循環、線性和竇性關聯方面性能優于RDC，而在二次和三次關聯方面性能略優于RDC。根據經驗，在一維數據，我們的χ2 估計與RDC有競爭關系，而其簡單和可微形式允許我們以合理的成本計算它。最近使用的一臺筆記本電腦上的pytorch，計算具有500個元組的HGR-KDE需要2.0ms，而已發布的RDC的numpy代碼需要4.6ms(平均運行1000次)。

?

4.2 基于Y和Z二值的公平性

本實驗中，我們解決了為訓練分類器的非線性神經網絡訓練懲罰的不同獨立測量，比如二值敏感信息Z不會影響結果Y不公平。為了證明此規范化與最新成果的二值變量有競爭關系，我們復現了另一個實驗。他們提出使用5個公開數據集。作為預處理步驟，我們對所有類別變量進行編碼并對數字條目進行標準化。

此處Y預測，我們使用網絡估計了Y=1的概率，見表1.

神經網絡和學習架構。我們為這些實驗提供了簡單的神經網絡：兩個隱藏層（第一層依賴于數據集大小有30到100個神經元，第二層比第一層小20個神經元）。代價是交叉熵，梯度是Adam,學習率值可能為10-2，10-4，3·10-4 。批量大小從{8,16,32,64,128}中選擇。為了避免KDE的估計問題——特別當Y=1時很少發生，我們總是估計128個為最小批量估計χ2 懲罰。λ設置為4*Renyi批量大小/批量大小。我們使用χ2作為HGR的平方，因為梯度值接近0在數值上越穩定。

5．結論

得益于HGR,我們從評估和學習的角度，統一和擴展了以前的框架，使其具有持續的敏感信息，從而實現算法的公平性。首先，我們提出了一個原則性的方法來推導公平目標的評價標準，這個標準可以寫成條件獨立。然后，對學習步驟進行了相應的推導。最后，我們實證地展示了在一系列問題(連續或非連續)上的性能以及對深度學習模型的適應性上的我們的方法。一個有趣的問題留給未來的工作是，是否可以用參數估計取代非參數密度估計，以改善方法的標度和減少方差的上下文中的小批處理。

? ? ? ?責任編輯:zl