擁有機器學習技能是不夠的。你還需要良好的數據結構的工作知識。學習更多,并解決一些問題。
因此,你已經決定不再使用固定的算法并開始編寫自己的機器學習方法。也許你已經有了一種新的集群數據的新方法,或者你可能對你最喜歡的統計分類包的局限性感到失望。
無論哪種情況,你對數據結構和算法的了解越多,在代碼編寫時就越容易。我不認為機器學習中使用的數據結構與其他軟件開發領域的數據結構有很大的不同。然而,由于許多問題的規模和難度,對基礎知識的掌握非常重要。
另外,由于機器學習是一個數學性非常強的領域,我們應該記住,數據結構是如何被用來解決數學問題的,以及它們是如何以自己的方式來處理數學問題的。有兩種方法可以對數據結構進行分類:通過它們的實現和它們的操作。
通過實現,我指的是它們的編程方式和實際存儲模式的具體細節。它們的外觀并沒有如何實現更重要。對于按操作或抽象數據類型分類的數據結構來說,情況恰恰相反——它們的外觀和操作比實現方式更重要,事實上,它們通常可以使用許多不同的內部表示來實現。
數組
當我說基本數組是機器學習中最重要的數據結構時,我并不是在開玩笑。這個實用的類型比你想象的要多。數組非常重要,因為它們被用于線性代數——這是你可以使用的最有用和最強大的數學工具。
因此,最常見的類型分別是一個和二維的類型,分別對應于向量和矩陣,但偶爾會遇到三個或四維的數組,它們要么用于更高級別的張量,要么為前者的組示例。
在進行矩陣運算時,你將不得不從令人眼花繚亂的各種庫、數據類型、甚至語言中進行選擇。許多科學編程語言,如Matlab,交互式數據語言(IDL),以及帶有Numpy擴展的Python,主要是為處理向量和矩陣而設計的。
但這些數據結構的優點是,即使在更通用的編程語言中,實現向量和矩陣在metal很簡單,假設語言中有任何Fortran DNA。考慮矩陣向量乘法的平移:
使用C++:
for (int i=0; i0;
for (int j=0; j
在大多數情況下,數組可以在運行時分配到固定大小,或者可以計算可靠的上限。在那些需要數組無限擴展的情況下,可以使用可擴展數組,例如C ++標準模板庫(STL)中的vector類。Matlab中的規則數組具有相似的可擴展性,可擴展數組是整個Python語言的基礎。
在這個數據結構中,有兩個元數據與實際數據值一起存儲。 這些是分配給數據結構的存儲空間量和陣列的實際大小。一旦數組大小超過存儲空間,將分配一個新空間,該空間的大小是其大小的兩倍,將值復制到其中,并刪除舊數組。
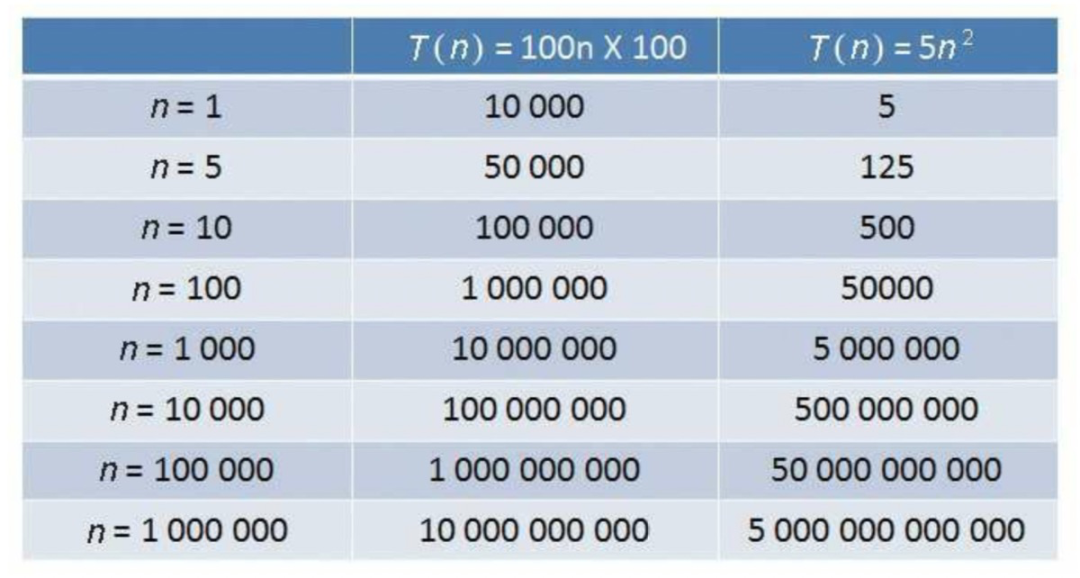
這有一個O(n)操作,其中n是數組的大小,但由于它只是偶爾發生,所以添加一個新值到實際結束的時間實際上被分配到常量時間O(1)。這是一個非常靈活的數據結構,具有快速的平均插入和快速訪問。
可擴展數組非常適合組成其他更復雜的數據結構并使其可擴展。例如,要存儲稀疏矩陣,可以在結尾添加任意數量的新元素,然后按位置對其進行排序以更快地定位。稍后詳述!稀疏矩陣可用于文本分類問題。
鏈表
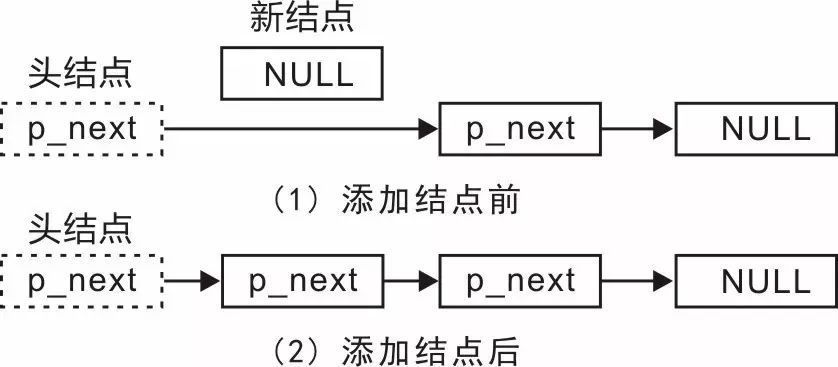
鏈表由幾個分開分配的節點組成。每個節點都包含一個數據值和一個指向列表中下一個節點的指針。插入在不變的時間是非常有效的,但是訪問一個值很慢,并且通常需要掃描大部分列表。
鏈表很容易拼接并分開。有許多變化——例如,可以在頭部或尾部進行插入;該列表可以是雙鏈接的,并且有許多類似的數據結構基于相同的原則。
主要是,我發現鏈表可用于解析不確定長度的列表。 之后,它們可以轉換為固定長度的陣列以便快速訪問。出于這個原因,我使用了一個鏈接列表類,其中包含一個轉換為數組的方法。
二叉樹
二叉樹與鏈表相似,只不過每個節點都有兩個指向后續節點的指針而不是一個。左側孩子的值總是小于父節點的值,而父節點的值又小于右側孩子的值。因此,二叉樹中的數據會自動排序。O(log n)的平均插入和訪問都是有效的。像鏈接列表一樣,它們很容易轉換為數組,這是樹狀排序的基礎。
平衡樹
如果數據已經排序,二叉樹在O(n)最差的情況下效率較低,因為數據將被線性排列,就好像它是一個鏈表。雖然二叉樹中的排序受到限制,但它絕不是唯一的,并且可以根據插入的順序以相同的列表排列許多不同的配置。
為了使其更加平衡,可以將一些轉換應用于樹。自平衡樹會自動執行這些操作,以保持訪問和插入的最佳平均值。
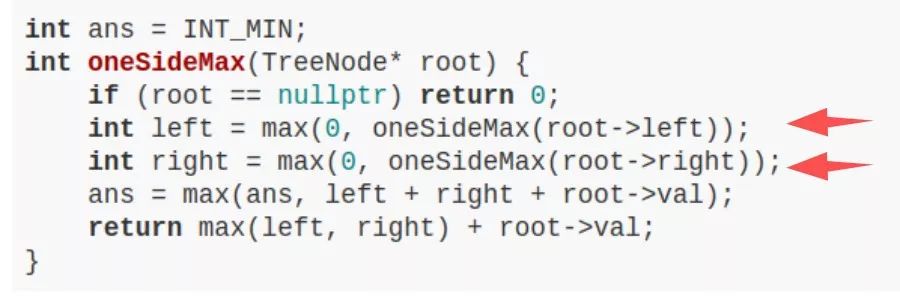
機器學習中普遍存在的問題是找到最接近某一特定點的鄰居。這個問題是NN算法所需要的。KD樹是一種二叉樹,它提供了一種有效的解決方案。
堆
堆是另一個層次結構,類似于樹的有序數據結構,它具有垂直排序,而不是水平排序。這種排序適用于層次結構,但不適用于整個層次:父節點總是大于它的子節點,但是更高級別的節點并不一定比下面的節點要大。
插入和檢索都是通過升級來執行的。元素首先插入到最高可用位置。然后將其與其父母進行比較并提升,直至達到正確的等級。為了從堆中去掉一個元素,兩個孩子中較大的一個被提升到缺失的位置,然后這兩個孩子中較大的一個被提升,如此等等,直到每一個都變成正確的等級。
通常情況下,頂部的最高排名值將從堆中取出,以便對列表進行排序。 與樹不同,大多數堆只是簡單地存儲在數組中,元素之間的關系只是隱含的。
堆棧
一個堆棧被定義為“先進后出”。一個元素被壓入堆棧的頂部,覆蓋前一個元素。頂部的元素必須先彈出才能訪問任何其他元素。
堆棧主要用于解析語法和實現計算機語言。
在許多機器學習應用程序中,領域特定語言(DSL)是完美的解決方案。例如,libAGF庫使用遞歸控制語言將二進制分類一般化到多類。特殊字符用于重復前面的選項,但是由于語言是遞歸的,所以必須從相同的層次或更高的層次上選擇該選項。這是由堆棧實現的。
隊列
隊列被定義為“先入先出”。想想銀行柜員面前的隊伍(對于我們這些年紀還大的人來說,還記得在網上銀行出現之前的一段時間)。隊列在實時編程中非常有用,因此程序可以維護要處理的作業列表。
考慮一個記錄運動員分段時間的應用程序。你輸入bib號碼,然后按回車鍵,但你要做的時候,后面的運動員也通過了。所以你輸入的是最近接近運動員的bib號碼列表,然后按下一個單獨的鍵來注冊隊列中的下一個。
集合
一個集合包含一個非重復元素的無序列表。如果添加已經在集合中的元素,則不會有任何更改。由于機器學習的許多數學知識都與集合有關,所以它們是非常有用的數據結構。
關聯數組
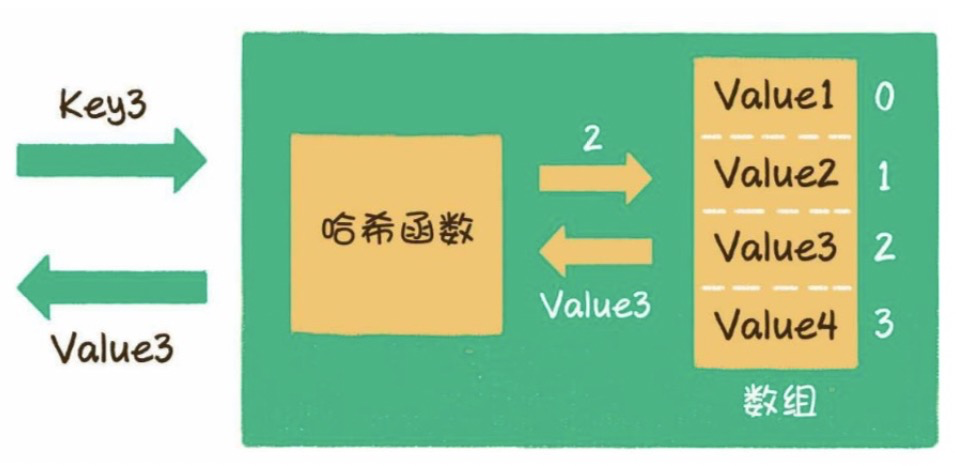
在關聯數組中,有兩種類型的數據成對存儲:密鑰及其相關值。 數據結構本質上是關系型的:數值由其鍵來解決。由于大部分訓練數據也是關系型的,這種類型的數據結構似乎非常適合于機器學習問題。在實踐中,它的用處不大,部分原因是大多數關聯數組只是一維的,而機器學習數據通常是多維的。
關聯數組適用于構建字典。假設你正在構建一個DSL,想要存儲一個函數和變量列表,并且需要區分這兩者。
sin =函數。
var = 變量。
exp =函數。
x =變量。
sqrt =函數。
a =變量。
在“sqrt”查詢數組將返回“函數”。
自定義數據結構
當你處理更多問題時,你肯定會遇到標準配方框不包含最佳結構的那些問題。你將需要設計自己的數據結構。考慮一個多類分類器,它概括了一個二元分類器來處理具有兩個以上類的分類問題。一個明顯的解決方案是平分:遞歸地將類分成兩組。但分層解決方案并不是解決多類的唯一方法,你可以使用類似于二叉樹的方法來組織二進制分類器。考慮幾個分區,然后用它們同時解決所有類的概率。
最通用的解決方案將兩者結合起來,因此每個分層分區不需要是二進制的,而是可以通過非分層多類分類器來解決。這是在libAGF庫中采用的方法。
更復雜的數據結構也可以由基本結構組成。考慮一個稀疏矩陣類。在稀疏矩陣中,大多數元素都是零,并且只存儲非零元素。我們可以將每個元素的位置和值存儲為一個三元組,并將它們的列表存儲在一個可擴展數組中。
結論
數據結構本身偶爾也很有趣。令它們真正有趣的是它們可以解決的各種問題。對于大多數工作,我使用了許多基本的固定長度數組。我主要使用更復雜的數據結構來使程序在運行和與外部界面交互方面更加流暢,并且更加便于用戶使用。不像以前的Fortran程序那樣,為了改變網格大小,我不得不忍受一個接近半小時的編譯周期(我實際上在這樣的程序上工作過!)。
即使你無法想出一個應用程序,我仍然認為知道諸如棧和隊列之類的東西是件好事。你永遠不知道什么時候會派上用場。真正復雜的人工智能應用程序可能會使用定向和無向圖,它們只是樹和鏈表的一般化。如果你無法應對后者,你將如何建立起像前者那樣的東西?
問題
如果你想自己練習和實現ML算法的數據結構,請嘗試解決下面的一些問題:
將矩陣向量乘法代碼片段封裝到名為matrix_times_vector的子例程中。設計子例程的調用語法。使用struct,typedef或class,將矢量和矩陣分別封裝到一對稱為vect和matrix的抽象類型中。為這些類型設計一個API。在網上找到至少三個以上的庫。
下載并安裝LIBSVM庫。考慮方法Kernel :: k_function在“svm.cpp”的第316行。用于保存向量的數據結構有哪些優缺點?在LIBSVM庫中,如何重構內核函數的計算?文中描述的哪些數據結構是抽象類型?你可以使用什么內部表示/數據結構來實現抽象數據類型?上面的列表中是否有未包含的內容?
使用二叉樹,設計一個關聯數組。
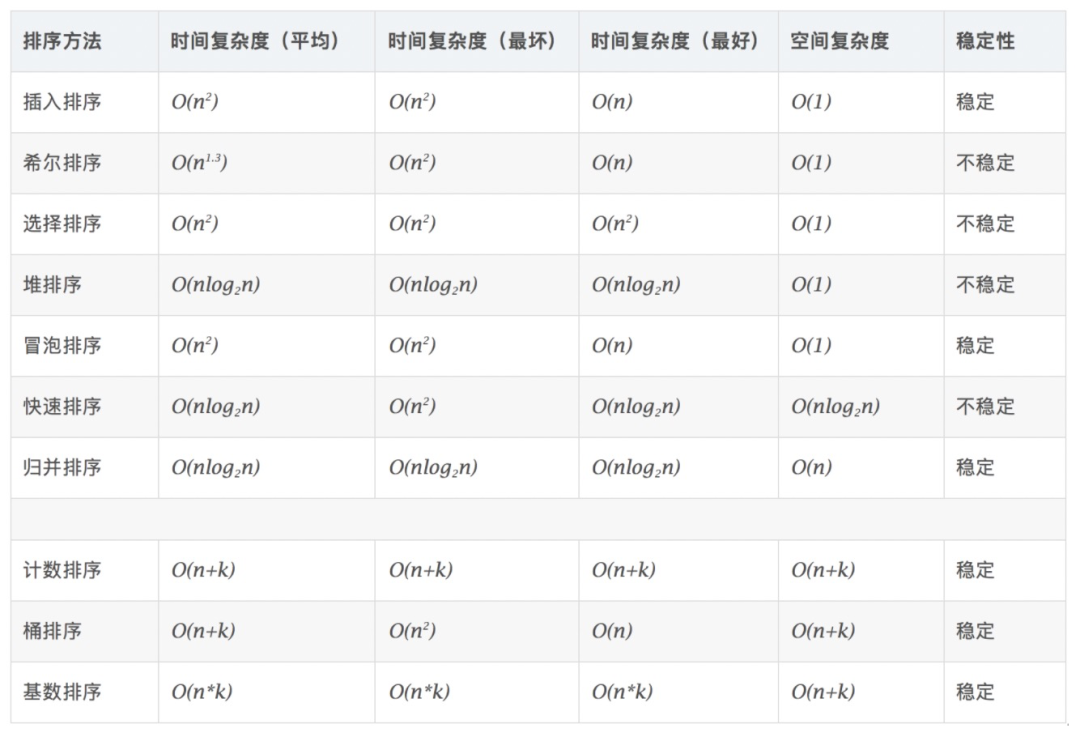
在LIBSVM中考慮向量類型。如何用它來表示一個稀疏矩陣?與上面描述的稀疏矩陣類進行對比。看看完整的類型。每個代表的優點和缺點是什么?實現一個treesort和一個堆排序。現在使用相同的數據結構來查找前k個元素。什么常見的機器學習算法適合這種情況?用你喜歡的語言實現你最喜歡的數據結構。
責任編輯:ct
 電子發燒友App
電子發燒友App
























評論