?
二叉樹的統一迭代法
此時我們在二叉樹:一入遞歸深似海,從此offer是路人中用遞歸的方式,實現了二叉樹前中后序的遍歷。
在二叉樹:聽說遞歸能做的,棧也能做!中用棧實現了二叉樹前后中序的迭代遍歷(非遞歸)。
之后我們發現迭代法實現的先中后序,其實風格也不是那么統一,除了先序和后序,有關聯,中序完全就是另一個風格了,一會用棧遍歷,一會又用指針來遍歷。
實踐過的同學,也會發現使用迭代法實現先中后序遍歷,很難寫出統一的代碼,不像是遞歸法,實現了其中的一種遍歷方式,其他兩種只要稍稍改一下節點順序就可以了。
其實針對三種遍歷方式,使用迭代法是可以寫出統一風格的代碼!
重頭戲來了,接下來介紹一下統一寫法。
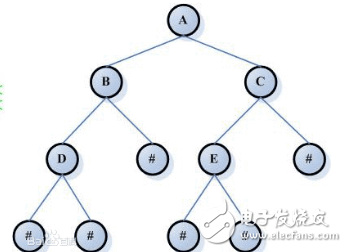
我們以中序遍歷為例,在二叉樹:聽說遞歸能做的,棧也能做!中提到說使用棧的話,無法同時解決訪問節點(遍歷節點)和處理節點(將元素放進結果集)不一致的情況。
那我們就將訪問的節點放入棧中,把要處理的節點也放入棧中但是要做標記。
如何標記呢,就是要處理的節點放入棧之后,緊接著放入一個空指針作為標記。?這種方法也可以叫做標記法。
迭代法中序遍歷
中序遍歷代碼如下:(詳細注釋)
class?Solution?{
public:
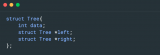
????vector<int>?inorderTraversal(TreeNode*?root)?{
????????vector<int>?result;
????????stack?st;
????????if?(root?!=?NULL)?st.push(root);
????????while?(!st.empty())?{
????????????TreeNode*?node?=?st.top();
????????????if?(node?!=?NULL)?{
????????????????st.pop();?//?將該節點彈出,避免重復操作,下面再將右中左節點添加到棧中
????????????????if?(node->right)?st.push(node->right);??//?添加右節點(空節點不入棧)
????????????????st.push(node);??????????????????????????//?添加中節點
????????????????st.push(NULL);?//?中節點訪問過,但是還沒有處理,加入空節點做為標記。
????????????????if?(node->left)?st.push(node->left);????//?添加左節點(空節點不入棧)
????????????}?else?{?//?只有遇到空節點的時候,才將下一個節點放進結果集
????????????????st.pop();???????????//?將空節點彈出
????????????????node?=?st.top();????//?重新取出棧中元素
????????????????st.pop();
????????????????result.push_back(node->val);?//?加入到結果集
????????????}
????????}
????????return?result;
????}
};
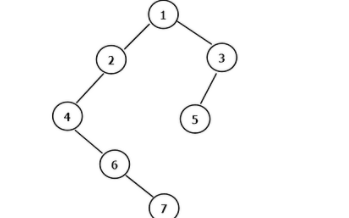
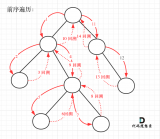
看代碼有點抽象我們來看一下動畫(中序遍歷):
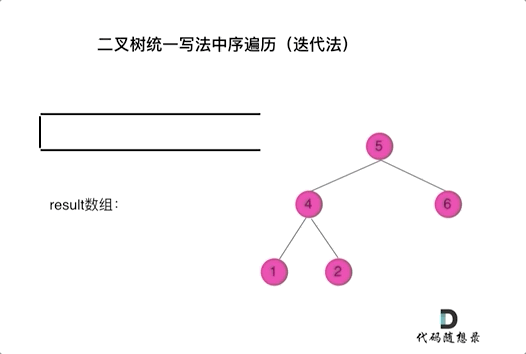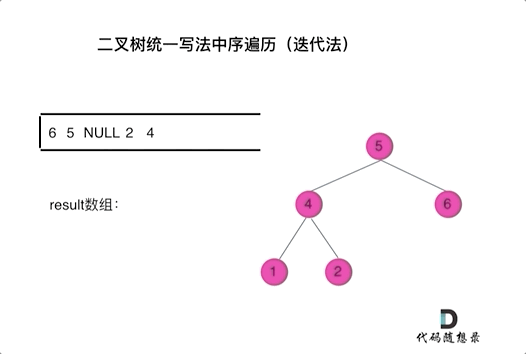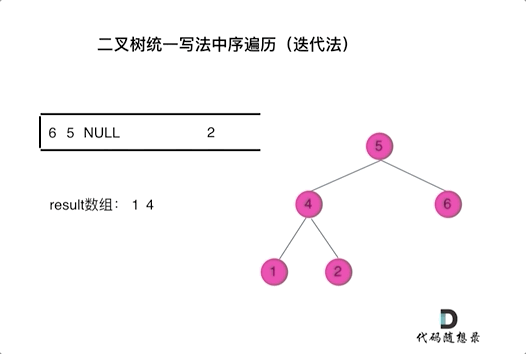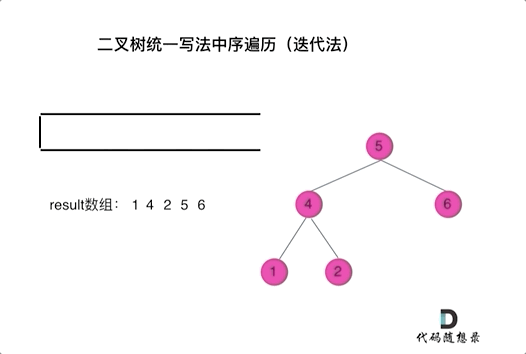 中序遍歷迭代(統一寫法)
中序遍歷迭代(統一寫法)動畫中,result數組就是最終結果集。
可以看出我們將訪問的節點直接加入到棧中,但如果是處理的節點則后面放入一個空節點, 這樣只有空節點彈出的時候,才將下一個節點放進結果集。
此時我們再來看前序遍歷代碼。
迭代法前序遍歷
迭代法前序遍歷代碼如下:(注意此時我們和中序遍歷相比僅僅改變了兩行代碼的順序)
class?Solution?{
public:
????vector<int>?preorderTraversal(TreeNode*?root)?{
????????vector<int>?result;
????????stack?st;
????????if?(root?!=?NULL)?st.push(root);
????????while?(!st.empty())?{
????????????TreeNode*?node?=?st.top();
????????????if?(node?!=?NULL)?{
????????????????st.pop();
????????????????if?(node->right)?st.push(node->right);??//?右
????????????????if?(node->left)?st.push(node->left);????//?左
????????????????st.push(node);??????????????????????????//?中
????????????????st.push(NULL);
????????????}?else?{
????????????????st.pop();
????????????????node?=?st.top();
????????????????st.pop();
????????????????result.push_back(node->val);
????????????}
????????}
????????return?result;
????}
};
迭代法后序遍歷
后續遍歷代碼如下:(注意此時我們和中序遍歷相比僅僅改變了兩行代碼的順序)
class?Solution?{
public:
????vector<int>?postorderTraversal(TreeNode*?root)?{
????????vector<int>?result;
????????stack?st;
????????if?(root?!=?NULL)?st.push(root);
????????while?(!st.empty())?{
????????????TreeNode*?node?=?st.top();
????????????if?(node?!=?NULL)?{
????????????????st.pop();
????????????????st.push(node);??????????????????????????//?中
????????????????st.push(NULL);
????????????????if?(node->right)?st.push(node->right);??//?右
????????????????if?(node->left)?st.push(node->left);????//?左
????????????}?else?{
????????????????st.pop();
????????????????node?=?st.top();
????????????????st.pop();
????????????????result.push_back(node->val);
????????????}
????????}
????????return?result;
????}
};
總結
此時我們寫出了統一風格的迭代法,不用在糾結于前序寫出來了,中序寫不出來的情況了。
但是統一風格的迭代法并不好理解,而且想在面試直接寫出來還有難度的。
所以大家根據自己的個人喜好,對于二叉樹的前中后序遍歷,選擇一種自己容易理解的遞歸和迭代法。
其他語言版本
Java:迭代法前序遍歷代碼如下:
class?Solution?{
????public?List?preorderTraversal(TreeNode?root)? {
????????List?result?=?new?LinkedList<>();
????????Stack?st?=?new?Stack<>();
????????if?(root?!=?null)?st.push(root);
????????while?(!st.empty())?{
????????????TreeNode?node?=?st.peek();
????????????if?(node?!=?null)?{
????????????????st.pop();?//?將該節點彈出,避免重復操作,下面再將右中左節點添加到棧中
????????????????if?(node.right!=null)?st.push(node.right);??//?添加右節點(空節點不入棧)
????????????????if?(node.left!=null)?st.push(node.left);????//?添加左節點(空節點不入棧)
????????????????st.push(node);??????????????????????????//?添加中節點
????????????????st.push(null);?//?中節點訪問過,但是還沒有處理,加入空節點做為標記。
????????????????
????????????}?else?{?//?只有遇到空節點的時候,才將下一個節點放進結果集
????????????????st.pop();???????????//?將空節點彈出
????????????????node?=?st.peek();????//?重新取出棧中元素
????????????????st.pop();
????????????????result.add(node.val);?//?加入到結果集
????????????}
????????}
????????return?result;
????}
}
迭代法中序遍歷代碼如下:
class?Solution?{
public?List?inorderTraversal(TreeNode?root)? {
????????List?result?=?new?LinkedList<>();
????Stack?st?=?new?Stack<>();
????if?(root?!=?null)?st.push(root);
????while?(!st.empty())?{
????????TreeNode?node?=?st.peek();
????????if?(node?!=?null)?{
????????????st.pop();?//?將該節點彈出,避免重復操作,下面再將右中左節點添加到棧中
????????????if?(node.right!=null)?st.push(node.right);??//?添加右節點(空節點不入棧)
????????????st.push(node);??????????????????????????//?添加中節點
????????????st.push(null);?//?中節點訪問過,但是還沒有處理,加入空節點做為標記。
????????????if?(node.left!=null)?st.push(node.left);????//?添加左節點(空節點不入棧)
????????}?else?{?//?只有遇到空節點的時候,才將下一個節點放進結果集
????????????st.pop();???????????//?將空節點彈出
????????????node?=?st.peek();????//?重新取出棧中元素
????????????st.pop();
????????????result.add(node.val);?//?加入到結果集
????????}
????}
????return?result;
}
}
迭代法后序遍歷代碼如下:
class?Solution?{
???public?List?postorderTraversal(TreeNode?root)? {
????????List?result?=?new?LinkedList<>();
????????Stack?st?=?new?Stack<>();
????????if?(root?!=?null)?st.push(root);
????????while?(!st.empty())?{
????????????TreeNode?node?=?st.peek();
????????????if?(node?!=?null)?{
????????????????st.pop();?//?將該節點彈出,避免重復操作,下面再將右中左節點添加到棧中
????????????????st.push(node);??????????????????????????//?添加中節點
????????????????st.push(null);?//?中節點訪問過,但是還沒有處理,加入空節點做為標記。
????????????????if?(node.right!=null)?st.push(node.right);??//?添加右節點(空節點不入棧)
????????????????if?(node.left!=null)?st.push(node.left);????//?添加左節點(空節點不入棧)?????????
???????????????????????????????
????????????}?else?{?//?只有遇到空節點的時候,才將下一個節點放進結果集
????????????????st.pop();???????????//?將空節點彈出
????????????????node?=?st.peek();????//?重新取出棧中元素
????????????????st.pop();
????????????????result.add(node.val);?//?加入到結果集
????????????}
????????}
????????return?result;
???}
}
迭代法前序遍歷:
class?Solution:
????def?preorderTraversal(self,?root:?TreeNode)?->?List[int]:
????????result?=?[]
????????st=?[]
????????if?root:
????????????st.append(root)
????????while?st:
????????????node?=?st.pop()
????????????if?node?!=?None:
????????????????if?node.right:?#右
????????????????????st.append(node.right)
????????????????if?node.left:?#左
????????????????????st.append(node.left)
????????????????st.append(node)?#中
????????????????st.append(None)
????????????else:
????????????????node?=?st.pop()
????????????????result.append(node.val)
????????return?result
迭代法中序遍歷:
class?Solution:
????def?inorderTraversal(self,?root:?TreeNode)?->?List[int]:
????????result?=?[]
????????st?=?[]
????????if?root:
????????????st.append(root)
????????while?st:
????????????node?=?st.pop()
????????????if?node?!=?None:
????????????????if?node.right:?#添加右節點(空節點不入棧)
????????????????????st.append(node.right)
????????????????
????????????????st.append(node)?#添加中節點
????????????????st.append(None)?#中節點訪問過,但是還沒有處理,加入空節點做為標記。
????????????????
????????????????if?node.left:?#添加左節點(空節點不入棧)
????????????????????st.append(node.left)
????????????else:?#只有遇到空節點的時候,才將下一個節點放進結果集
????????????????node?=?st.pop()?#重新取出棧中元素
????????????????result.append(node.val)?#加入到結果集
????????return?result
迭代法后序遍歷:
class?Solution:
????def?postorderTraversal(self,?root:?TreeNode)?->?List[int]:
????????result?=?[]
????????st?=?[]
????????if?root:
????????????st.append(root)
????????while?st:
????????????node?=?st.pop()
????????????if?node?!=?None:
????????????????st.append(node)?#中
????????????????st.append(None)
????????????????
????????????????if?node.right:?#右
????????????????????st.append(node.right)
????????????????if?node.left:?#左
????????????????????st.append(node.left)
????????????else:
????????????????node?=?st.pop()
????????????????result.append(node.val)
????????return?result
?
?審核編輯 :李倩
 電子發燒友App
電子發燒友App



































評論