數(shù)學(xué)家酷愛漂亮的謎題。當(dāng)你嘗試找到最有效的方法時，即使像乘法矩陣（二維數(shù)字表）這樣抽象的東西也會感覺像玩一場游戲。這有點像嘗試用盡可能少的步驟解開魔方——具有挑戰(zhàn)性，但也很誘人。除了魔方，每一步可能的步數(shù)為 18；對于矩陣乘法，即使在相對簡單的情況下，每一步都可以呈現(xiàn)超過 10^12 個選項。

在過去的 50 年里，研究人員以多種方式解決了這個問題，所有這些都是基于人類直覺輔助的計算機搜索。2022 年 10 月，人工智能公司 DeepMind 的一個團隊展示了如何從一個新的方向解決這個問題，在《Nature》雜志的一篇論文中報告說，他們已經(jīng)成功地訓(xùn)練了一個神經(jīng)網(wǎng)絡(luò)來發(fā)現(xiàn)新的快速矩陣乘法算法。就仿佛 AI 找到了解決極其復(fù)雜的魔方的未知策略。

https://www.nature.com/articles/s41586-022-05172-4

「這是一個非常巧妙的結(jié)果。」哥倫比亞大學(xué)計算機科學(xué)家 Josh Alman 說，但他和其他矩陣乘法專家也強調(diào)，這種人工智能輔助將補充而不是取代現(xiàn)有方法——至少在短期內(nèi)是這樣。「這就像對可能成為突破的事物的概念驗證。」Alman 說。結(jié)果只會幫助研究人員完成他們的任務(wù)。

仿佛是為了證明這一點，《自然》雜志的論文發(fā)表三天后，兩位奧地利研究人員展示了新舊方法如何相互補充。他們使用傳統(tǒng)的計算機輔助搜索來進(jìn)一步改進(jìn)神經(jīng)網(wǎng)絡(luò)發(fā)現(xiàn)的一種算法。

https://arxiv.org/pdf/2210.04045.pdf

結(jié)果表明，就像解決魔方的過程一樣，通往更好算法的道路將充滿曲折。

乘法矩陣

矩陣乘法是所有數(shù)學(xué)中最基本和最普遍的運算之一。要將一對 n×n 矩陣相乘，每個矩陣都有 n^2 個元素，你可以將這些元素以特定組合相乘并相加以生成乘積，即第三個 n×n 矩陣。將兩個 n×n 矩陣相乘的標(biāo)準(zhǔn)方法需要 n^3 次乘法運算，因此，例如，一個 2×2 矩陣需要八次乘法。

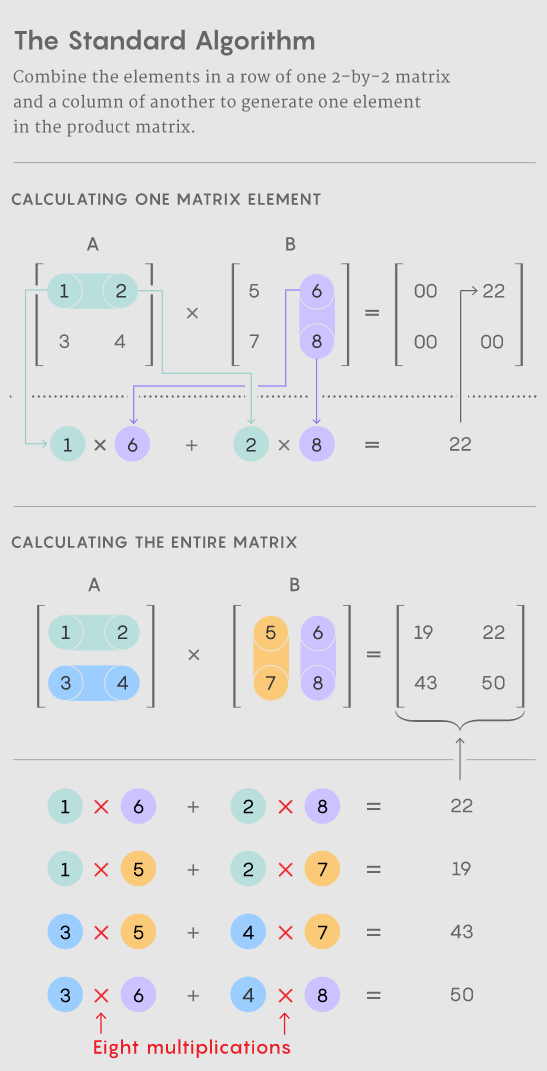
對于具有數(shù)千行和列的較大矩陣，此過程很快就會變得麻煩。但在 1969 年，數(shù)學(xué)家 Volker Strassen 發(fā)現(xiàn)了一種使用七個而不是八個乘法步驟將一對 2×2 矩陣相乘的過程，代價是引入了更多的加法步驟。

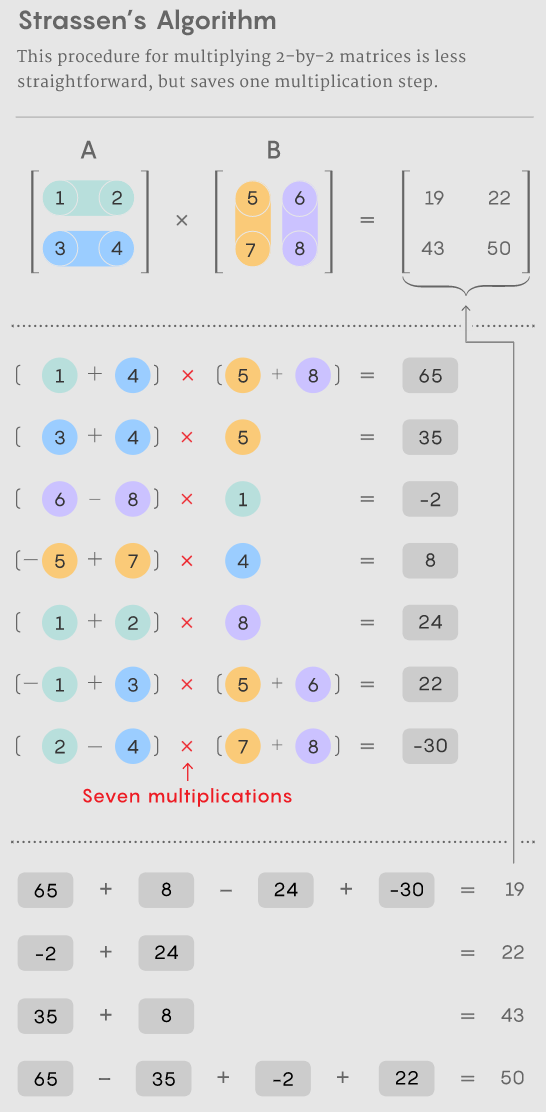
如果你只想乘以一對 2×2 矩陣，則 Strassen 算法不必要地復(fù)雜化。但他意識到它也適用于更大的矩陣。那是因為矩陣的元素本身可以是矩陣。例如，可以將具有 20,000 行和 20,000 列的矩陣重新設(shè)想為一個 2×2 矩陣，其四個元素各為 10,000×10,000 矩陣。然后可以將這些矩陣中的每一個細(xì)分為四個 5,000×5,000 塊，依此類推。Strassen 可以應(yīng)用他的方法在此嵌套層次結(jié)構(gòu)的每一層上乘以 2×2 矩陣。隨著矩陣大小的增加，減少乘法所節(jié)省的成本也會增加。

Strassen 的發(fā)現(xiàn)促使人們開始尋找高效的矩陣乘法算法，此后啟發(fā)了兩個不同的子領(lǐng)域。一個側(cè)重于一個原則問題：如果你想象將兩個 n×n 矩陣相乘并讓 n 趨于無窮大，那么最快的算法中的乘法步驟數(shù)如何與 n 成比例？

最佳縮放比例的當(dāng)前記錄 n^2.3728596 屬于麻省理工學(xué)院計算機科學(xué)家 Alman 和 Virginia Vassilevska Williams。（最近發(fā)布的預(yù)印本報告了使用新技術(shù)的微小改進(jìn)。）但這些算法純粹是理論上的興趣，僅在荒謬的大矩陣上勝過 Strassen 等方法。

https://arxiv.org/abs/2210.10173

第二個子領(lǐng)域的思考規(guī)模較小。在 Strassen 的工作之后不久，以色列裔美國計算機科學(xué)家 Shmuel Winograd 表明 Strassen 已經(jīng)達(dá)到了理論極限：不可能用少于七個乘法步驟來乘以 2×2 矩陣。但對于所有其他矩陣大小，所需乘法的最小數(shù)量仍然是一個懸而未決的問題。小矩陣的快速算法可能會產(chǎn)生巨大的影響，因為當(dāng)乘以合理大小的矩陣時，這種算法的重復(fù)迭代可能會擊敗 Strassen 的算法。

https://www.sciencedirect.com/science/article/pii/0024379571900097

不幸的是，可能性的數(shù)量是巨大的。即使對于 3×3 矩陣，「可能的算法數(shù)量也超過了宇宙中的原子數(shù)量，」DeepMind 研究員兼新工作的負(fù)責(zé)人之一 Alhussein Fawzi 說。

面對這些令人眼花繚亂的選項，研究人員通過將矩陣乘法轉(zhuǎn)化為一個看起來完全不同的數(shù)學(xué)問題——一個計算機更容易處理的問題——取得了進(jìn)展。可以將兩個矩陣相乘的抽象任務(wù)表示為一種特定類型的數(shù)學(xué)對象：稱為張量的三維數(shù)字?jǐn)?shù)組。然后，研究人員可以將這個張量分解為基本分量的總和，稱為「rank-1」張量；這些中的每一個都代表相應(yīng)矩陣乘法算法中的不同步驟。這意味著找到一個有效的乘法算法相當(dāng)于最小化張量分解中的項數(shù)——項越少，涉及的步驟就越少。

通過這種方式，研究人員發(fā)現(xiàn)了新的算法，可以使用比標(biāo)準(zhǔn) n^3 更少的乘法步驟來乘以許多小矩陣大小的 n×n 矩陣。但是，不僅優(yōu)于標(biāo)準(zhǔn)而且優(yōu)于 Strassen 小矩陣算法的算法仍然遙不可及——直到現(xiàn)在。

Game On

DeepMind 團隊通過將張量分解變成單人游戲來解決這個問題。他們從 AlphaGo 的深度學(xué)習(xí)算法入手——AlphaGo 是另一個 DeepMind AI，它在 2016 年學(xué)會了玩棋盤游戲 Go，足以擊敗頂尖的人類棋手。

所有的深度學(xué)習(xí)算法都是圍繞神經(jīng)網(wǎng)絡(luò)構(gòu)建的：人工神經(jīng)元網(wǎng)絡(luò)被分類成層，連接強度可以變化，代表每個神經(jīng)元對下一層神經(jīng)元的影響程度。這些連接的強度在訓(xùn)練過程的多次迭代中得到調(diào)整，在此期間神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)將它接收到的每個輸入轉(zhuǎn)換為有助于算法實現(xiàn)其總體目標(biāo)的輸出。

在 DeepMind 的新算法（稱為 AlphaTensor）中，輸入代表通往有效矩陣乘法方案的步驟。神經(jīng)網(wǎng)絡(luò)的第一個輸入是原始矩陣乘法張量，其輸出是 AlphaTensor 為其第一步選擇的 rank-1 張量。該算法從初始輸入中減去這個 rank-1 張量，產(chǎn)生一個更新的張量，該張量作為新輸入反饋到網(wǎng)絡(luò)中。重復(fù)該過程，直到最終起始張量中的每個元素都減少為零，這意味著沒有更多的 rank-1 張量可以取出。

在這一點上，神經(jīng)網(wǎng)絡(luò)發(fā)現(xiàn)了一個有效的張量分解，因為它在數(shù)學(xué)上保證了所有 rank-1 張量的總和恰好等于起始張量。到達(dá)那里所采取的步驟可以轉(zhuǎn)換回相應(yīng)的矩陣乘法算法的步驟。

游戲是這樣的：AlphaTensor 反復(fù)將張量分解為一組 rank-1 分量。每次，如果 AlphaTensor 找到減少步數(shù)的方法，它就會獲得獎勵。但勝利的捷徑一點也不直觀，就像你有時必須在魔方上拼湊出一張完美有序的臉，然后才能解決整個問題。

該團隊現(xiàn)在有了一種算法，理論上可以解決他們的問題。他們只需要先訓(xùn)練它。

新路徑

與所有神經(jīng)網(wǎng)絡(luò)一樣，AlphaTensor 需要大量數(shù)據(jù)進(jìn)行訓(xùn)練，但張量分解是一個眾所周知的難題。研究人員可以為網(wǎng)絡(luò)提供有效分解的例子很少。相反，他們通過在更簡單的逆問題上進(jìn)行訓(xùn)練來幫助算法開始：將一堆隨機生成的 rank-1 張量相加。

布朗大學(xué)計算機科學(xué)家 Michael Littman 說：「他們正在使用簡單的問題為困難的問題生成更多數(shù)據(jù)。」將這種向后訓(xùn)練過程與強化學(xué)習(xí)相結(jié)合，其中 AlphaTensor 在尋找有效分解時會產(chǎn)生自己的訓(xùn)練數(shù)據(jù)，其效果比單獨使用任何一種訓(xùn)練方法都要好得多。

DeepMind 團隊訓(xùn)練 AlphaTensor 來分解代表矩陣乘法的張量，最高可達(dá) 12×12。它尋求用于將普通實數(shù)矩陣相乘的快速算法，以及特定于更受約束的設(shè)置（稱為模 2 運算）的算法。（這是僅基于兩個數(shù)字的數(shù)學(xué)，因此矩陣元素只能是 0 或 1，并且 1 + 1 = 0。）研究人員通常從這個更受限制但仍然廣闊的空間開始，希望這里發(fā)現(xiàn)的算法可以適用于實數(shù)矩陣。

訓(xùn)練后，AlphaTensor 在幾分鐘內(nèi)重新發(fā)現(xiàn)了 Strassen 的算法。然后，它針對每種矩陣大小發(fā)現(xiàn)了多達(dá)數(shù)千種新的快速算法。這些與最著名的算法不同，但乘法步驟數(shù)相同。

在少數(shù)情況下，AlphaTensor 甚至打破了現(xiàn)有記錄。它最令人驚訝的發(fā)現(xiàn)發(fā)生在模 2 運算中，它發(fā)現(xiàn)了一種新算法，可以在 47 個乘法步驟中將 4×4 矩陣相乘，比 Strassen 算法兩次迭代所需的 49 個步驟有所改進(jìn)。它還打破了最著名的 5×5 模 2 矩陣算法，將所需的乘法次數(shù)從之前的 98 次記錄減少到 96 次。（但這個新記錄仍然落后于使用 5×5 矩陣擊敗 Strassen 算法所需的 91 步。）

這一引人注目的新結(jié)果引起了很多興奮，一些研究人員對基于 AI 的現(xiàn)狀改進(jìn)大加贊賞。但并非矩陣乘法領(lǐng)域中的每個人都對此印象深刻。「我覺得它有點被夸大了，」Vassilevska Williams 說。「這是另一種工具。這不像是，[哦，計算機打敗了人類，] 你知道嗎？」

研究人員還強調(diào)，破紀(jì)錄的 4×4 算法的直接應(yīng)用將受到限制：它不僅只在模 2 算法中有效，而且在現(xiàn)實生活中，除了速度之外還有其他重要的考慮因素。

Fawzi 也認(rèn)為，這僅僅是個開始。「有很大的改進(jìn)和研究空間，這是一件好事，」他說。

最后的轉(zhuǎn)折

相對于成熟的計算機搜索方法，AlphaTensor 的最大優(yōu)勢也是它最大的弱點：它不受人類直覺的約束，無法判斷好的算法是什么樣子的，因此它無法解釋自己的選擇。這使得研究人員很難從其成就中學(xué)習(xí)。

但這可能并沒有看上去那么大的缺點。在 AlphaTensor 結(jié)果公布幾天后，奧地利林茨大學(xué)（JKU）的數(shù)學(xué)家 Manuel Kauers 和他的研究生 Jakob Moosbauer 報告說又向前邁進(jìn)了一步。

Manuel Kauers 調(diào)整了 DeepMind 的方法以產(chǎn)生進(jìn)一步的改進(jìn)。——Jakob Moosbauer

當(dāng) DeepMind 論文發(fā)表時，Kauers 和 Moosbauer 正在使用傳統(tǒng)的計算機輔助搜索來尋找新的乘法算法。但與大多數(shù)以新的指導(dǎo)原則重新開始的此類搜索不同，他們的方法通過反復(fù)調(diào)整現(xiàn)有算法來工作，希望從中節(jié)省更多的乘法。以 AlphaTensor 的 5×5 模 2 矩陣算法為起點，他們驚奇地發(fā)現(xiàn)，他們的方法在短短幾秒鐘的計算之后，就將乘法步驟從 96 步減少到了 95 步。

AlphaTensor 還間接幫助他們進(jìn)行了另一項改進(jìn)。此前，Kauers 和 Moosbauer 并沒有費心去探索 4×4 矩陣的空間，他們認(rèn)為不可能擊敗 Strassen 算法的兩次迭代。AlphaTensor 的結(jié)果促使他們重新考慮，在從頭開始計算一周后，他們的方法出現(xiàn)了另一種 47 步算法，與 AlphaTensor 發(fā)現(xiàn)的算法無關(guān)。「如果有人告訴我們 4×4 有什么值得發(fā)現(xiàn)的東西，我們本可以早點做到這一點，」Kauers 說。「但是，好吧，這就是它的工作原理。」

Littman 預(yù)計會有更多這樣的驚喜，他將這種情況比作跑步者第一次在四分鐘內(nèi)跑完一英里，這一壯舉曾被廣泛認(rèn)為是不可能的。「人們就像，[哦，等等，我們可以做到這一點，] 現(xiàn)在很多人都可以做到，」他說。

展望未來，F(xiàn)awzi 希望推廣 AlphaTensor 以解決更廣泛的數(shù)學(xué)和計算任務(wù)，就像它的祖先 AlphaGo 最終擴展到其他游戲一樣。

Kauers 認(rèn)為這是將機器學(xué)習(xí)應(yīng)用于發(fā)現(xiàn)新算法的真正試金石。他指出，尋求快速矩陣乘法算法是一個組合問題，無論有無人工協(xié)助，計算機搜索都非常適合。但并不是所有的數(shù)學(xué)問題都那么容易確定。他說，如果機器學(xué)習(xí)能夠發(fā)現(xiàn)一種全新的算法理念，「這將改變游戲規(guī)則。」

編輯：黃飛

?