transformer結構是google在17年的Attention Is All You Need論文中提出,在NLP的多個任務上取得了非常好的效果,可以說目前NLP發展都離不開transformer。最大特點是拋棄了傳統的CNN和RNN,整個網絡結構完全是由Attention機制組成。由于其出色性能以及對下游任務的友好性或者說下游任務僅僅微調即可得到不錯效果,在計算機視覺領域不斷有人嘗試將transformer引入,近期也出現了一些效果不錯的嘗試,典型的如目標檢測領域的detr和可變形detr,分類領域的vision transformer等等。本文從transformer結構出發,結合視覺中的transformer成果(具體是vision transformer和detr)進行分析,希望能夠幫助cv領域想了解transformer的初學者快速入門。由于本人接觸transformer時間也不長,也算初學者,故如果有描述或者理解錯誤的地方歡迎指正。
本文的大部分圖來自論文、國外博客和國內翻譯博客,在此一并感謝前人工作,具體鏈接見參考資料。本文特別長,大概有3w字,請先點贊收藏然后慢慢看....
1 transformer介紹
一般講解transformer都會以機器翻譯任務為例子講解,機器翻譯任務是指將一種語言轉換得到另一種語言,例如英語翻譯為中文任務。從最上層來看,如下所示:

1.1 早期seq2seq
機器翻譯是一個歷史悠久的問題,本質可以理解為序列轉序列問題,也就是我們常說的seq2seq結構,也可以稱為encoder-decoder結構,如下所示:
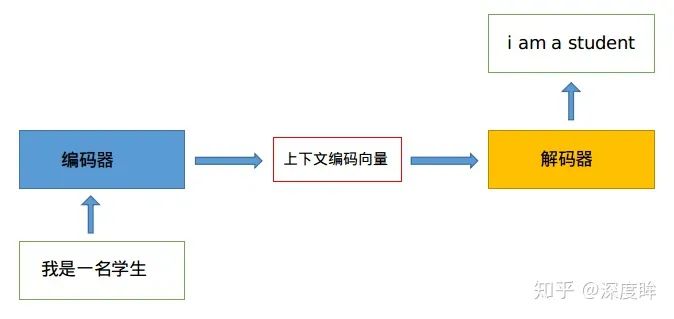
encoder和decoder在早期一般是RNN模塊(因為其可以捕獲時序信息),后來引入了LSTM或者GRU模塊,不管內部組件是啥,其核心思想都是通過Encoder編碼成一個表示向量,即上下文編碼向量,然后交給Decoder來進行解碼,翻譯成目標語言。一個采用典型RNN進行編碼碼翻譯的可視化圖如下:
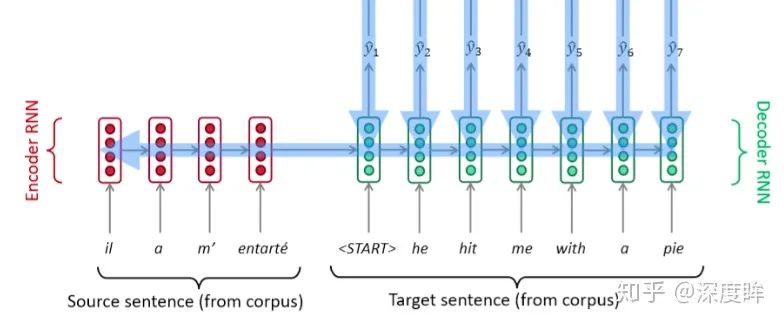
可以看出,其解碼過程是順序進行,每次僅解碼出一個單詞。對于CV領域初學者來說,RNN模塊構建的seq2seq算法,理解到這個程度就可以了,不需要深入探討如何進行訓練。但是上述結構其實有缺陷,具體來說是:
不論輸入和輸出的語句長度是什么,中間的上下文向量長度都是固定的,一旦長度過長,僅僅靠一個固定長度的上下文向量明顯不合理
僅僅利用上下文向量解碼,會有信息瓶頸,長度過長時候信息可能會丟失
通俗理解是編碼器與解碼器的連接點僅僅是編碼單元輸出的隱含向量,其包含的信息有限,對于一些復雜任務可能信息不夠,如要翻譯的句子較長時,一個上下文向量可能存不下那么多信息,就會造成翻譯精度的下降。
1.2 基于attention的seq2seq
基于上述缺陷進而提出帶有注意力機制Attention的seq2seq,同樣可以應用于RNN、LSTM或者GRU模塊中。注意力機制Attention對人類來說非常好理解,假設給定一張圖片,我們會自動聚焦到一些關鍵信息位置,而不需要逐行掃描全圖。此處的attention也是同一個意思,其本質是對輸入的自適應加權,結合cv領域的senet中的se模塊就能夠理解了。
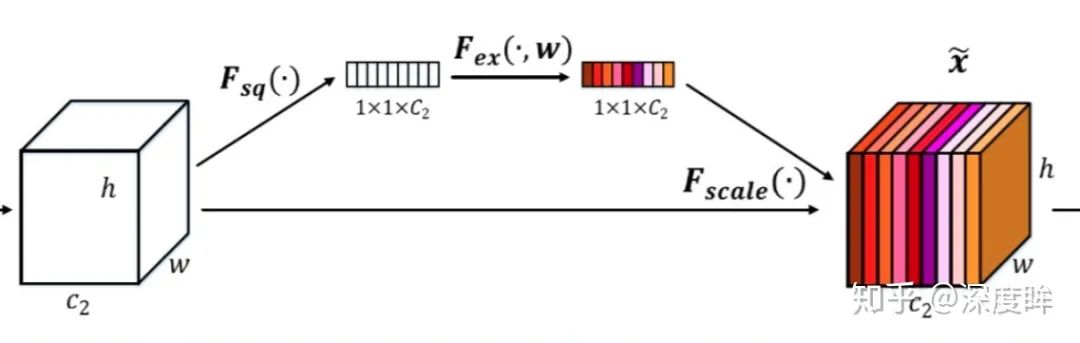
se模塊最終是學習出一個1x1xc的向量,然后逐通道乘以原始輸入,從而對特征圖的每個通道進行加權即通道注意力,對attention進行抽象,不管啥領域其機制都可以歸納為下圖:
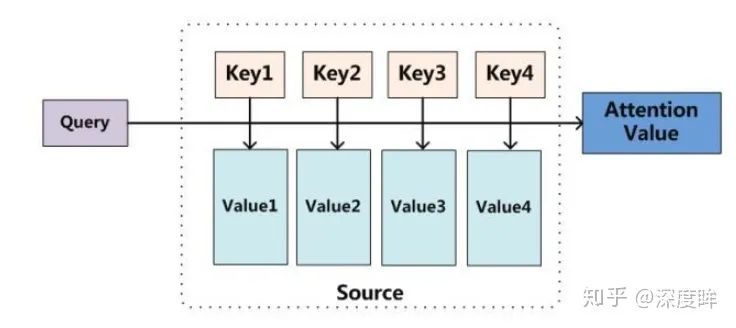
將Query(通常是向量)和4個Key(和Q長度相同的向量)分別計算相似性,然后經過softmax得到q和4個key相似性的概率權重分布,然后對應權重乘以Value(和Q長度相同的向量),最后相加即可得到包含注意力的attention值輸出,理解上應該不難。舉個簡單例子說明:
假設世界上所有小吃都可以被標簽化,例如微辣、特辣、變態辣、微甜、有嚼勁....,總共有1000個標簽,現在我想要吃的小吃是[微辣、微甜、有嚼勁],這三個單詞就是我的Query
來到東門老街一共100家小吃點,每個店鋪賣的東西不一樣,但是肯定可以被標簽化,例如第一家小吃被標簽化后是[微辣、微咸],第二家小吃被標簽化后是[特辣、微臭、特咸],第二家小吃被標簽化后是[特辣、微甜、特咸、有嚼勁],其余店鋪都可以被標簽化,每個店鋪的標簽就是Keys,但是每家店鋪由于賣的東西不一樣,單品種類也不一樣,所以被標簽化后每一家的標簽List不一樣長
Values就是每家店鋪對應的單品,例如第一家小吃的Values是[烤羊肉串、炒花生]
將Query和所有的Keys進行一一比對,相當于計算相似性,此時就可以知道我想買的小吃和每一家店鋪的匹配情況,最后有了匹配列表,就可以去店鋪里面買東西了(Values和相似性加權求和)。最終的情況可能是,我在第一家店鋪買了烤羊肉串,然后在第10家店鋪買了個玉米,最后在第15家店鋪買了個烤面筋
以上就是完整的注意力機制,采用我心中的標準Query去和被標簽化的所有店鋪Keys一一比對,此時就可以得到我的Query在每個店鋪中的匹配情況,最終去不同店鋪買不同東西的過程就是權重和Values加權求和過程。簡要代碼如下:
# 假設q是(1,N,512),N就是最大標簽化后的list長度,k是(1,M,512),M可以等于N,也可以不相等
# (1,N,512) x (1,512,M)-->(1,N,M)
attn = torch.matmul(q, k.transpose(2, 3))
# softmax轉化為概率,輸出(1,N,M),表示q中每個n和每個m的相關性
attn=F.softmax(attn, dim=-1)
# (1,N,M) x (1,M,512)-->(1,N,512),V和k的shape相同
output = torch.matmul(attn, v)
帶有attention的RNN模塊組成的ser2seq,解碼時候可視化如下:
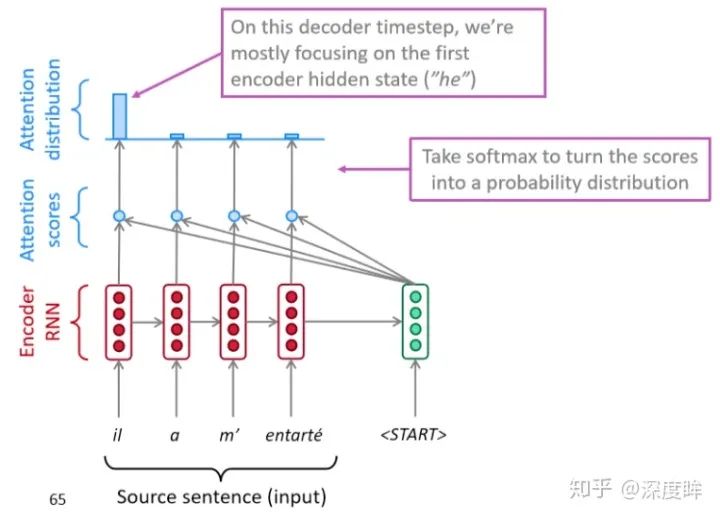
在沒有attention時候,不同解碼階段都僅僅利用了同一個編碼層的最后一個隱含輸出,加入attention后可以通過在每個解碼時間步輸入的都是不同的上下文向量,以上圖為例,解碼階段會將第一個開啟解碼標志(也就是Q)與編碼器的每一個時間步的隱含狀態(一系列Key和Value)進行點乘計算相似性得到每一時間步的相似性分數,然后通過softmax轉化為概率分布,然后將概率分布和對應位置向量進行加權求和得到新的上下文向量,最后輸入解碼器中進行解碼輸出,其詳細解碼可視化如下:
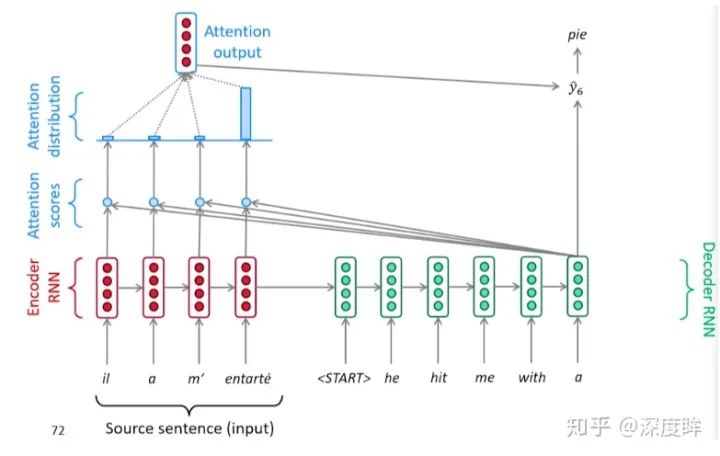
通過上述簡單的attention引入,可以將機器翻譯性能大幅提升,引入attention有以下幾個好處:
注意力顯著提高了機器翻譯性能
注意力允許解碼器以不同程度的權重利用到編碼器的所有信息,可以繞過瓶頸
通過檢查注意力分布,可以看到解碼器在關注什么,可解釋性強
1.3 基于transformer的seq2seq
基于attention的seq2seq的結構雖然說解決了很多問題,但是其依然存在不足:
不管是采用RNN、LSTM還是GRU都不利于并行訓練和推理,因為相關算法只能從左向右依次計算或者從右向左依次計算
長依賴信息丟失問題,順序計算過程中信息會丟失,雖然LSTM號稱有緩解,但是無法徹底解決
最大問題應該是無法并行訓練,不利于大規模快速訓練和部署,也不利于整個算法領域發展,故在Attention Is All You Need論文中拋棄了傳統的CNN和RNN,將attention機制發揮到底,整個網絡結構完全是由Attention機制組成,這是一個比較大的進步。
google所提基于transformer的seq2seq整體結構如下所示:
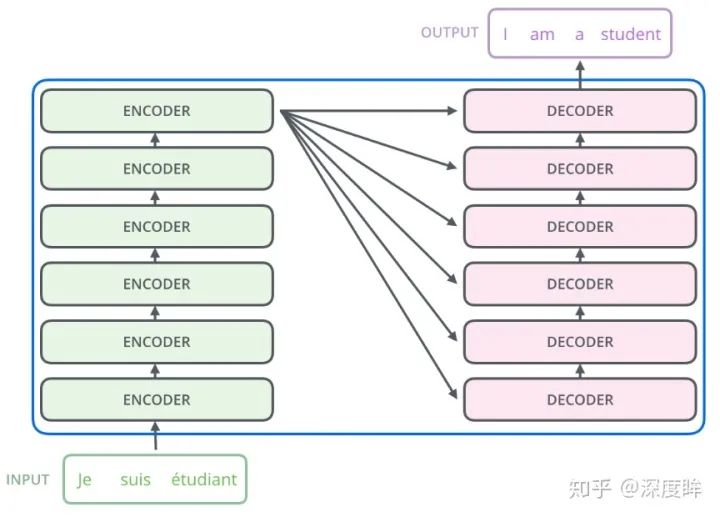
其包括6個結構完全相同的編碼器,和6個結構完全相同的解碼器,其中每個編碼器和解碼器設計思想完全相同,只不過由于任務不同而有些許區別,整體詳細結構如下所示:
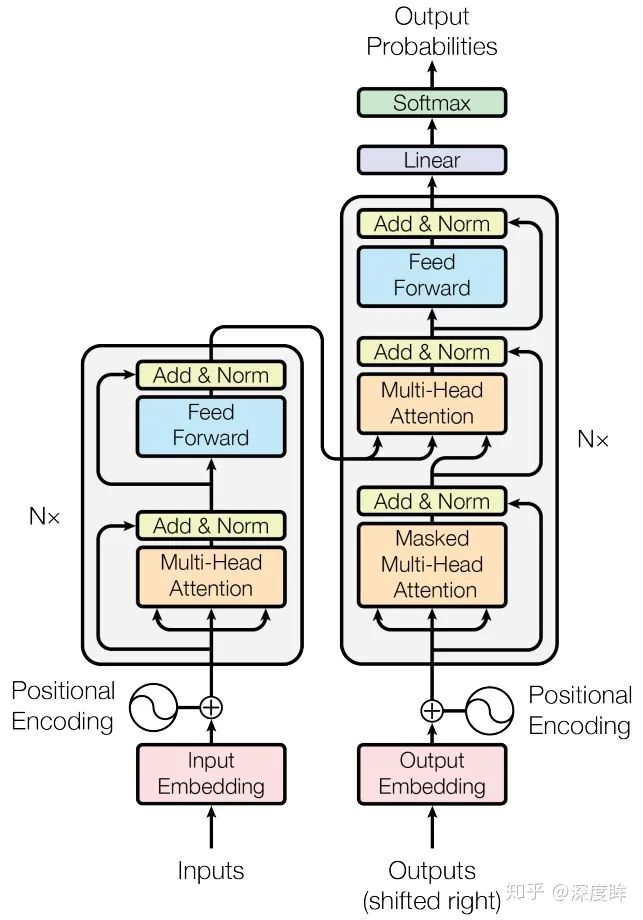
第一眼看有點復雜,其中N=6,由于基于transformer的翻譯任務已經轉化為分類任務(目標翻譯句子有多長,那么就有多少個分類樣本),故在解碼器最后會引入fc+softmax層進行概率輸出,訓練也比較簡單,直接采用ce loss即可,對于采用大量數據訓練好的預訓練模型,下游任務僅僅需要訓練fc層即可。上述結構看起來有點復雜,一個稍微抽象點的圖示如下:
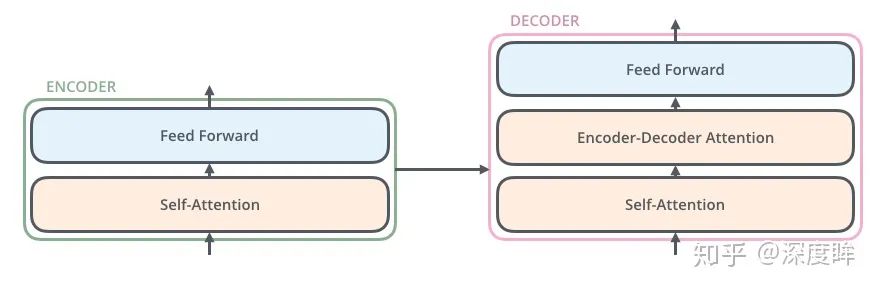
看起來比基于RNN或者其余結構構建的seq2seq簡單很多。下面結合代碼和原理進行深入分析。
1.4 transformer深入分析
前面寫了一大堆,沒有理解沒有關系,對于cv初學者來說其實只需要理解QKV的含義和注意力機制的三個計算步驟:Q和所有K計算相似性;對相似性采用softmax轉化為概率分布;將概率分布和V進行一一對應相乘,最后相加得到新的和Q一樣長的向量輸出即可,重點是下面要講的transformer結構。
下面按照?編碼器輸入數據處理->編碼器運行->解碼器輸入數據處理->解碼器運行->分類head?的實際運行流程進行講解。
1.4.1 編碼器輸入數據處理
(1) 源單詞嵌入
以上面翻譯任務為例,原始待翻譯輸入是三個單詞:

輸入是三個單詞,為了能夠將文本內容輸入到網絡中肯定需要進行向量化(不然單詞如何計算?),具體是采用nlp領域的embedding算法進行詞嵌入,也就是常說的Word2Vec。對于cv來說知道是干嘛的就行,不必了解細節。假設每個單詞都可以嵌入成512個長度的向量,故此時輸入即為3x512,注意Word2Vec操作只會輸入到第一個編碼器中,后面的編碼器接受的輸入是前一個編碼器輸出。
為了便于組成batch(不同訓練句子單詞個數肯定不一樣)進行訓練,可以簡單統計所有訓練句子的單詞個數,取最大即可,假設統計后發現待翻譯句子最長是10個單詞,那么編碼器輸入是10x512,額外填充的512維向量可以采用固定的標志編碼得到,例如$$。
(2) 位置編碼positional encoding
采用經過單詞嵌入后的向量輸入到編碼器中還不夠,因為transformer內部沒有類似RNN的循環結構,沒有捕捉順序序列的能力,或者說無論句子結構怎么打亂,transformer都會得到類似的結果。為了解決這個問題,在編碼詞向量時會額外引入了位置編碼position encoding向量表示兩個單詞i和j之間的距離,簡單來說就是在詞向量中加入了單詞的位置信息。
加入位置信息的方式非常多,最簡單的可以是直接將絕對坐標0,1,2編碼成512個長度向量即可。作者實際上提出了兩種方式:
網絡自動學習
自己定義規則
提前假設單詞嵌入并且組成batch后,shape為(b,N,512),N是序列最大長度,512是每個單詞的嵌入向量長度,b是batch
(a) 網絡自動學習
self.pos_embedding = nn.Parameter(torch.randn(1, N, 512))
比較簡單,因為位置編碼向量需要和輸入嵌入(b,N,512)相加,所以其shape為(1,N,512)表示N個位置,每個位置采用512長度向量進行編碼
(b) 自己定義規則
自定義規則做法非常多,論文中采用的是sin-cos規則,具體做法是:
將向量(N,512)采用如下函數進行處理
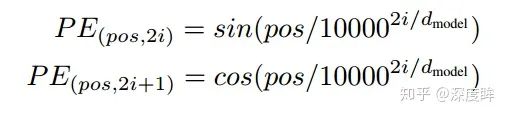
pos即0~N,i是0-511
將向量的512維度切分為奇數行和偶數行
偶數行采用sin函數編碼,奇數行采用cos函數編碼
然后按照原始行號拼接
def get_position_angle_vec(position):
# d_hid是0-511,position表示單詞位置0~N-1
return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]
# 每個單詞位置0~N-1都可以編碼得到512長度的向量
sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])
# 偶數列進行sin
sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2]) # dim 2i
# 奇數列進行cos
sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2]) # dim 2i+1
上面例子的可視化如下:
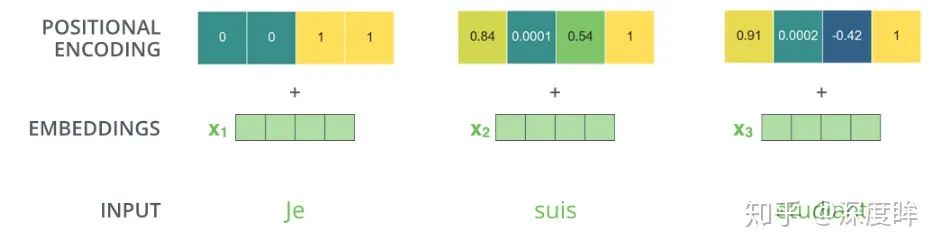
如此編碼的優點是能夠擴展到未知的序列長度,例如前向時候有特別長的句子,其可視化如下:
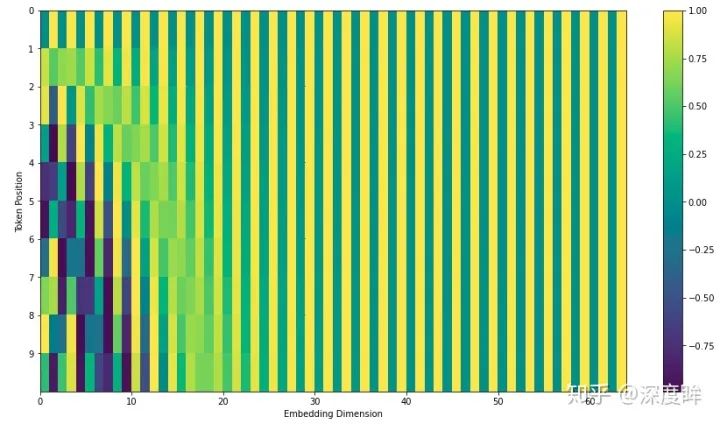
作者為啥要設計如此復雜的編碼規則?原因是sin和cos的如下特性:
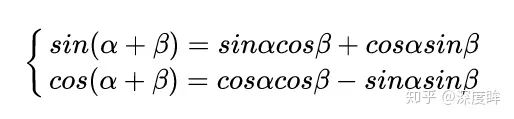
可以將用進行線性表出:
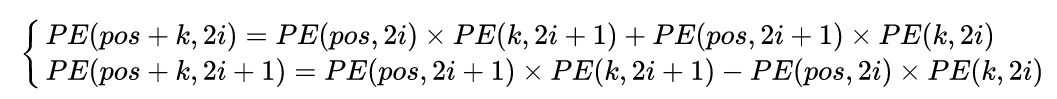
假設k=1,那么下一個位置的編碼向量可以由前面的編碼向量線性表示,等價于以一種非常容易學會的方式告訴了網絡單詞之間的絕對位置,讓模型能夠輕松學習到相對位置信息。注意編碼方式不是唯一的,將單詞嵌入向量和位置編碼向量相加就可以得到編碼器的真正輸入了,其輸出shape是(b,N,512)。
1.4.2 編碼器前向過程
編碼器由兩部分組成:自注意力層和前饋神經網絡層。
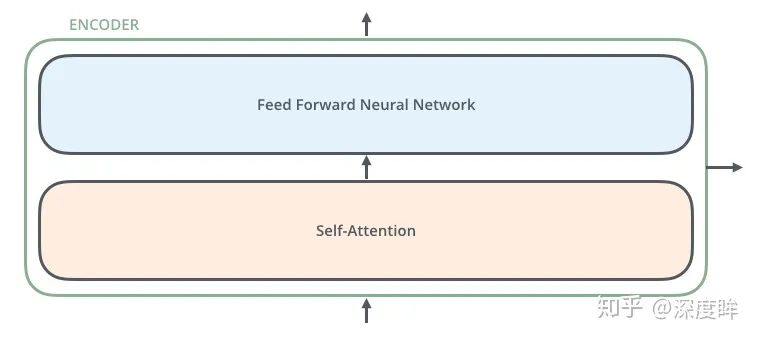
其前向可視化如下:
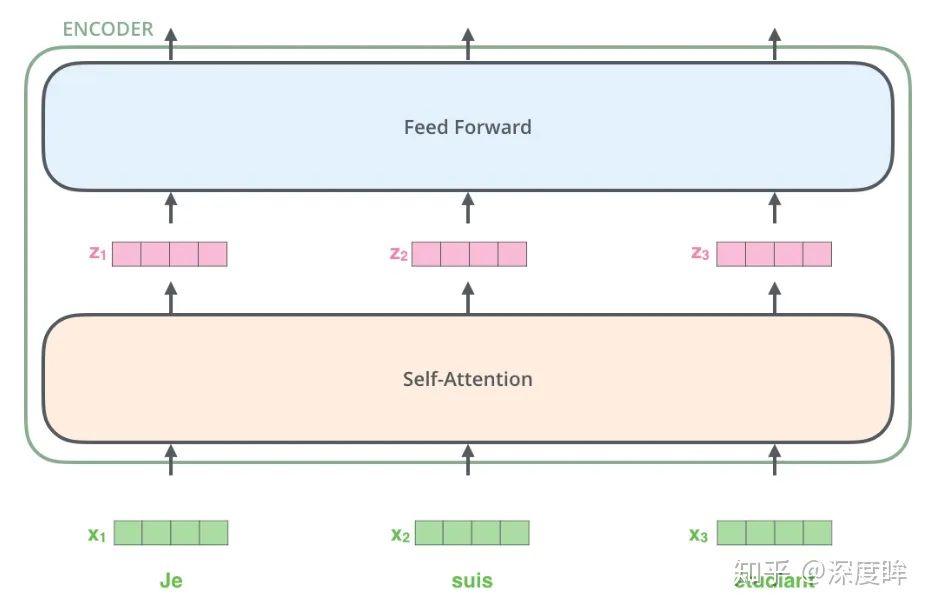
注意上圖沒有繪制出單詞嵌入向量和位置編碼向量相加過程,但是是存在的。
(1) 自注意力層
通過前面分析我們知道自注意力層其實就是attention操作,并且由于其QKV來自同一個輸入,故稱為自注意力層。我想大家應該能想到這里attention層作用,在參考資料1博客里面舉了個簡單例子來說明attention的作用:假設我們想要翻譯的輸入句子為The animal didn't cross the street because it was too tired,這個“it”在這個句子是指什么呢?它指的是street還是這個animal呢?這對于人類來說是一個簡單的問題,但是對于算法則不是。當模型處理這個單詞“it”的時候,自注意力機制會允許“it”與“animal”建立聯系即隨著模型處理輸入序列的每個單詞,自注意力會關注整個輸入序列的所有單詞,幫助模型對本單詞更好地進行編碼。實際上訓練完成后確實如此,google提供了可視化工具,如下所示:

上述是從宏觀角度思考,如果從輸入輸出流角度思考,也比較容易:
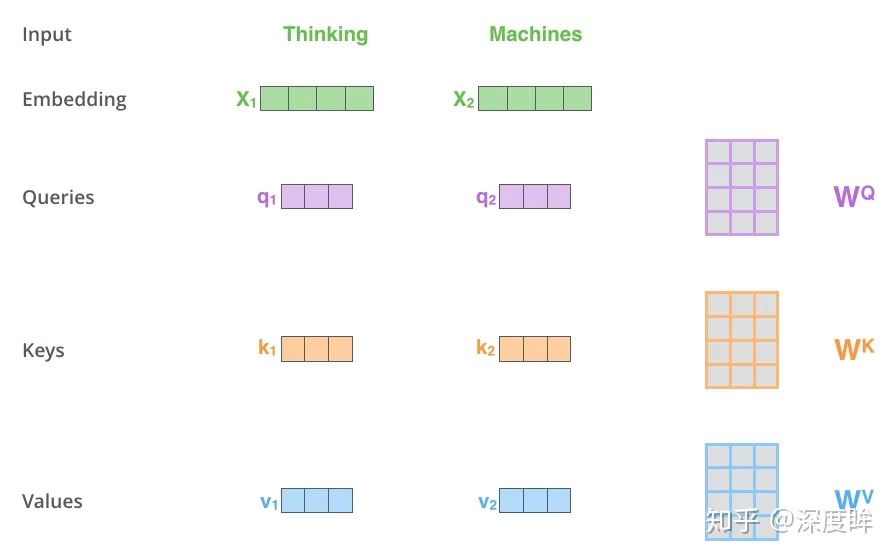
假設我們現在要翻譯上述兩個單詞,首先將單詞進行編碼,和位置編碼向量相加,得到自注意力層輸入X,其shape為(b,N,512);然后定義三個可學習矩陣??(通過nn.Linear實現),其shape為(512,M),一般M等于前面維度512,從而計算后維度不變;將X和矩陣
?相乘,得到QKV輸出,shape為(b,N,M);然后將Q和K進行點乘計算向量相似性;采用softmax轉換為概率分布;將概率分布和V進行加權求和即可。其可視化如下:
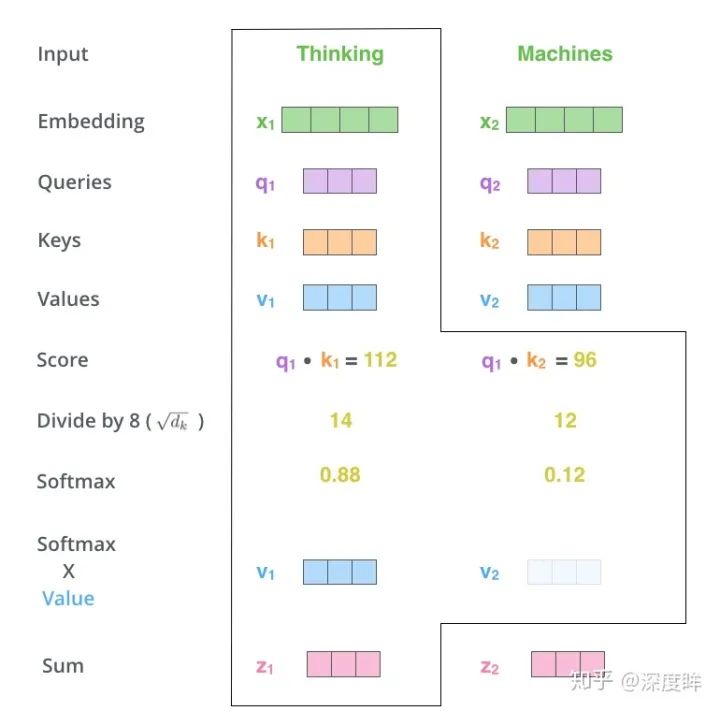
上述繪制的不是矩陣形式,更好理解而已。對于第一個單詞的編碼過程是:將q1和所有的k進行相似性計算,然后除以維度的平方根(論文中是64,本文可以認為是512)使得梯度更加穩定,然后通過softmax傳遞結果,這個softmax分數決定了每個單詞對編碼當下位置(“Thinking”)的貢獻,最后對加權值向量求和得到z1。
這個計算很明顯就是前面說的注意力機制計算過程,每個輸入單詞的編碼輸出都會通過注意力機制引入其余單詞的編碼信息。
上述為了方便理解才拆分這么細致,實際上代碼層面采用矩陣實現非常簡單:
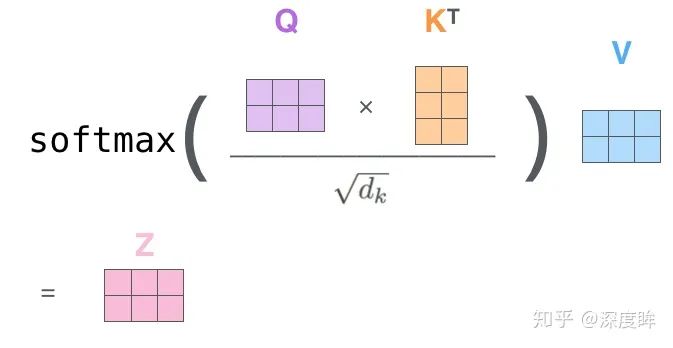
上面的操作很不錯,但是還有改進空間,論文中又增加一種叫做“多頭”注意力(“multi-headed” attention)的機制進一步完善了自注意力層,并在兩方面提高了注意力層的性能:
它擴展了模型專注于不同位置的能力。在上面的例子中,雖然每個編碼都在z1中有或多或少的體現,但是它可能被實際的單詞本身所支配。如果我們翻譯一個句子,比如“The animal didn’t cross the street because it was too tired”,我們會想知道“it”指的是哪個詞,這時模型的“多頭”注意機制會起到作用。
它給出了注意力層的多個“表示子空間",對于“多頭”注意機制,有多個查詢/鍵/值權重矩陣集(Transformer使用8個注意力頭,因此我們對于每個編碼器/解碼器有8個矩陣集合)。
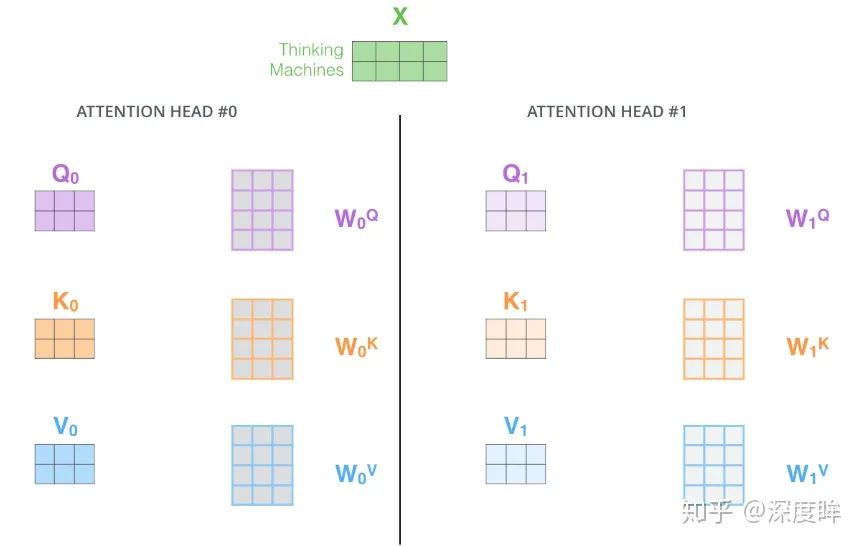
簡單來說就是類似于分組操作,將輸入X分別輸入到8個attention層中,得到8個Z矩陣輸出,最后對結果concat即可。論文圖示如下:
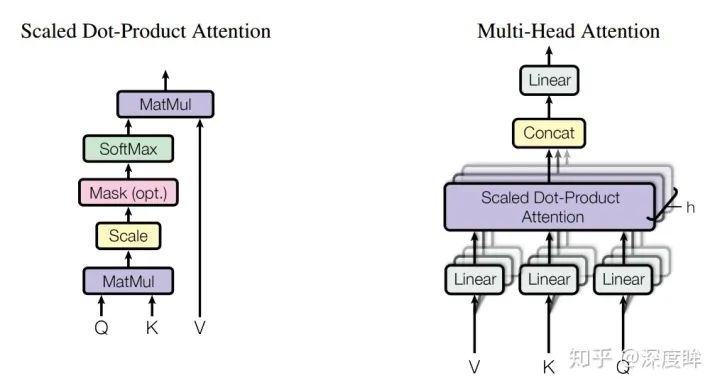
先忽略Mask的作用,左邊是單頭attention操作,右邊是n個單頭attention構成的多頭自注意力層。
代碼層面非常簡單,單頭attention操作如下:
class ScaledDotProductAttention(nn.Module):
''' Scaled Dot-Product Attention '''
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
# self.temperature是論文中的d_k ** 0.5,防止梯度過大
# QxK/sqrt(dk)
attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
if mask is not None:
# 屏蔽不想要的輸出
attn = attn.masked_fill(mask == 0, -1e9)
# softmax+dropout
attn = self.dropout(F.softmax(attn, dim=-1))
# 概率分布xV
output = torch.matmul(attn, v)
return output, attn
再次復習下Multi-Head Attention層的圖示,可以發現在前面講的內容基礎上還加入了殘差設計和層歸一化操作,目的是為了防止梯度消失,加快收斂。
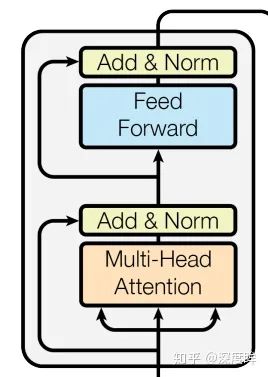
Multi-Head Attention實現在ScaledDotProductAttention基礎上構建:
class MultiHeadAttention(nn.Module):
''' Multi-Head Attention module '''
# n_head頭的個數,默認是8
# d_model編碼向量長度,例如本文說的512
# d_k, d_v的值一般會設置為 n_head * d_k=d_model,
# 此時concat后正好和原始輸入一樣,當然不相同也可以,因為后面有fc層
# 相當于將可學習矩陣分成獨立的n_head份
def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
super().__init__()
# 假設n_head=8,d_k=64
self.n_head = n_head
self.d_k = d_k
self.d_v = d_v
# d_model輸入向量,n_head * d_k輸出向量
# 可學習W^Q,W^K,W^V矩陣參數初始化
self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
# 最后的輸出維度變換操作
self.fc = nn.Linear(n_head * d_v, d_model, bias=False)
# 單頭自注意力
self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)
self.dropout = nn.Dropout(dropout)
# 層歸一化
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, q, k, v, mask=None):
# 假設qkv輸入是(b,100,512),100是訓練每個樣本最大單詞個數
# 一般qkv相等,即自注意力
residual = q
# 將輸入x和可學習矩陣相乘,得到(b,100,512)輸出
# 其中512的含義其實是8x64,8個head,每個head的可學習矩陣為64維度
# q的輸出是(b,100,8,64),kv也是一樣
q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)
# 變成(b,8,100,64),方便后面計算,也就是8個頭單獨計算
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)
if mask is not None:
mask = mask.unsqueeze(1) # For head axis broadcasting.
# 輸出q是(b,8,100,64),維持不變,內部計算流程是:
# q*k轉置,除以d_k ** 0.5,輸出維度是b,8,100,100即單詞和單詞直接的相似性
# 對最后一個維度進行softmax操作得到b,8,100,100
# 最后乘上V,得到b,8,100,64輸出
q, attn = self.attention(q, k, v, mask=mask)
# b,100,8,64-->b,100,512
q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)
q = self.dropout(self.fc(q))
# 殘差計算
q += residual
# 層歸一化,在512維度計算均值和方差,進行層歸一化
q = self.layer_norm(q)
return q, attn
現在pytorch新版本已經把MultiHeadAttention當做nn中的一個類了,可以直接調用。
(2) 前饋神經網絡層
這個層就沒啥說的了,非常簡單:
class PositionwiseFeedForward(nn.Module):
''' A two-feed-forward-layer module '''
def __init__(self, d_in, d_hid, dropout=0.1):
super().__init__()
# 兩個fc層,對最后的512維度進行變換
self.w_1 = nn.Linear(d_in, d_hid) # position-wise
self.w_2 = nn.Linear(d_hid, d_in) # position-wise
self.layer_norm = nn.LayerNorm(d_in, eps=1e-6)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
residual = x
x = self.w_2(F.relu(self.w_1(x)))
x = self.dropout(x)
x += residual
x = self.layer_norm(x)
return x
(3) 編碼層操作整體流程
可視化如下所示:
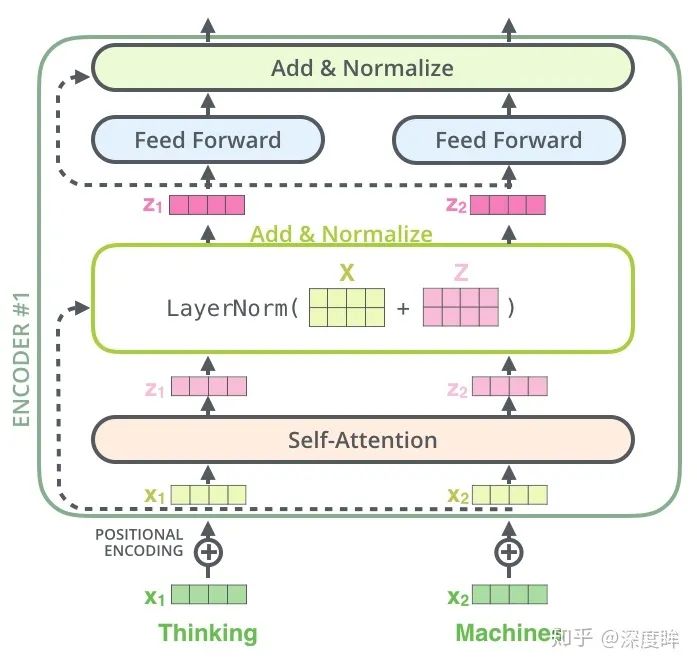
單個編碼層代碼如下所示:
class EncoderLayer(nn.Module):
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(EncoderLayer, self).__init__()
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
def forward(self, enc_input, slf_attn_mask=None):
# Q K V是同一個,自注意力
# enc_input來自源單詞嵌入向量或者前一個編碼器輸出
enc_output, enc_slf_attn = self.slf_attn(
enc_input, enc_input, enc_input, mask=slf_attn_mask)
enc_output = self.pos_ffn(enc_output)
return enc_output, enc_slf_attn
將上述編碼過程重復n遍即可,除了第一個模塊輸入是單詞嵌入向量與位置編碼的和外,其余編碼層輸入是上一個編碼器輸出即后面的編碼器輸入不需要位置編碼向量。如果考慮n個編碼器的運行過程,如下所示:
class Encoder(nn.Module):
def __init__(
self, n_src_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, dropout=0.1, n_position=200):
# nlp領域的詞嵌入向量生成過程(單詞在詞表里面的索引idx-->d_word_vec長度的向量)
self.src_word_emb = nn.Embedding(n_src_vocab, d_word_vec, padding_idx=pad_idx)
# 位置編碼
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
self.dropout = nn.Dropout(p=dropout)
# n個編碼器層
self.layer_stack = nn.ModuleList([
EncoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)])
# 層歸一化
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, src_seq, src_mask, return_attns=False):
# 對輸入序列進行詞嵌入,加上位置編碼
enc_output = self.dropout(self.position_enc(self.src_word_emb(src_seq)))
enc_output = self.layer_norm(enc_output)
# 作為編碼器層輸入
for enc_layer in self.layer_stack:
enc_output, _ = enc_layer(enc_output, slf_attn_mask=src_mask)
return enc_output
到目前為止我們就講完了編碼部分的全部流程和代碼細節。現在再來看整個transformer算法就會感覺親切很多了:
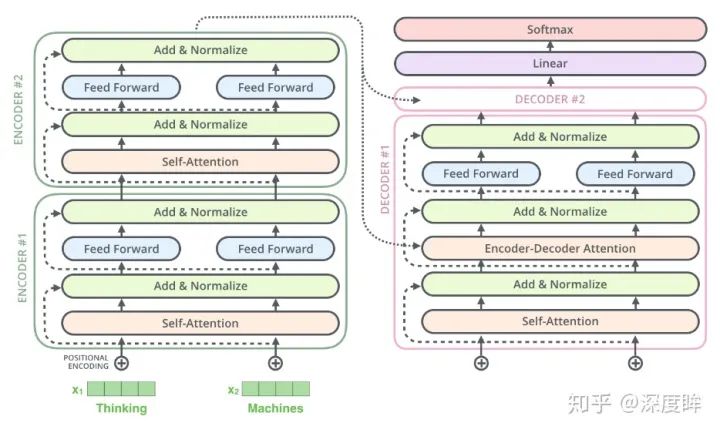
1.4.3 解碼器輸入數據處理
在分析解碼器結構前先看下解碼器整體結構,方便理解:
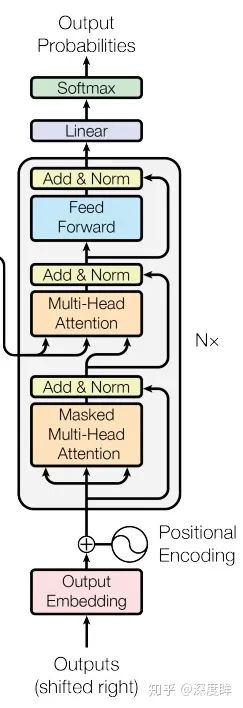
其輸入數據處理也要區分第一個解碼器和后續解碼器,和編碼器類似,第一個解碼器輸入不僅包括最后一個編碼器輸出,還需要額外的輸出嵌入向量,而后續解碼器輸入是來自最后一個編碼器輸出和前面解碼器輸出。
(1) 目標單詞嵌入
這個操作和源單詞嵌入過程完全相同,維度也是512,假設輸出是i am a student,那么需要對這4個單詞也利用word2vec算法轉化為4x512的矩陣,作為第一個解碼器的單詞嵌入輸入。
(2) 位置編碼
同樣的也需要對解碼器輸入引入位置編碼,做法和編碼器部分完全相同,且將目標單詞嵌入向量和位置編碼向量相加即可作為第一個解碼器輸入。
和編碼器單詞嵌入不同的地方是在進行目標單詞嵌入前,還需要將目標單詞即是i am a student右移動一位,新增加的一個位置采用提前定義好的標志位BOS_WORD代替,現在就變成[BOS_WORD,i,am,a,student],為啥要右移?因為解碼過程和seq2seq一樣是順序解碼的,需要提供一個開始解碼標志,。不然第一個時間步的解碼單詞i是如何輸出的呢?具體解碼過程其實是:輸入BOS_WORD,解碼器輸出i;輸入前面已經解碼的BOS_WORD和i,解碼器輸出am...,輸入已經解碼的BOS_WORD、i、am、a和student,解碼器輸出解碼結束標志位EOS_WORD,每次解碼都會利用前面已經解碼輸出的所有單詞嵌入信息
下面有個非常清晰的gif圖,一目了然:
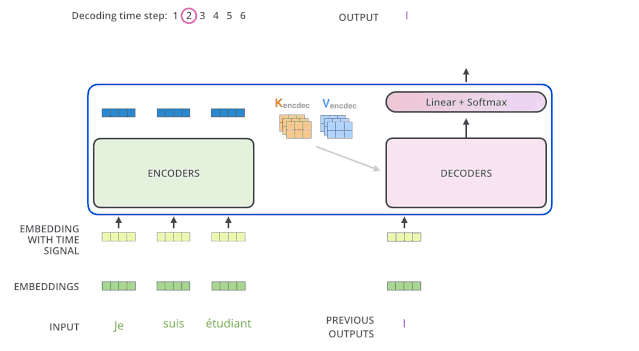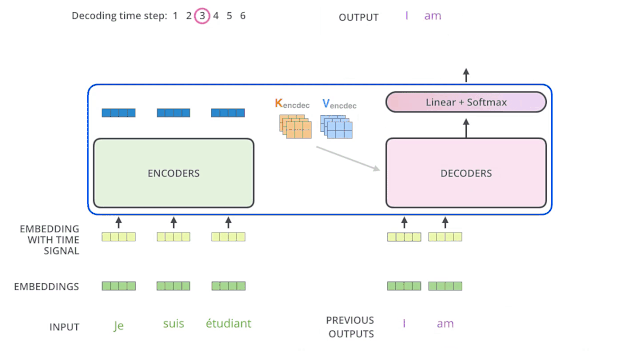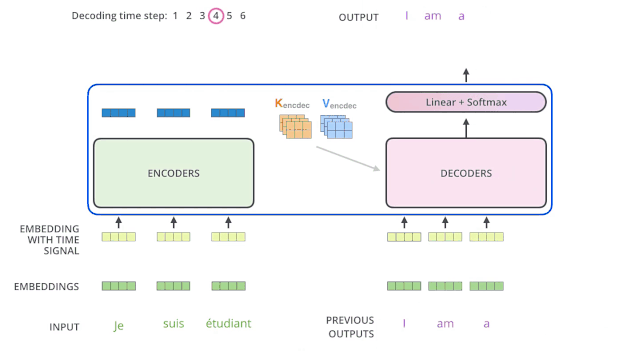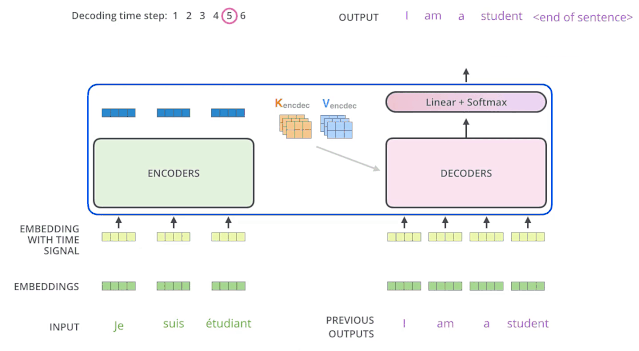
上圖沒有繪制BOS_WORD嵌入向量輸入,然后解碼出i單詞的過程。
1.4.4 解碼器前向過程
仔細觀察解碼器結構,其包括:帶有mask的MultiHeadAttention、MultiHeadAttention和前饋神經網絡層三個組件,帶有mask的MultiHeadAttention和MultiHeadAttention結構和代碼寫法是完全相同,唯一區別是是否輸入了mask。
為啥要mask?原因依然是順序解碼導致的。試想模型訓練好了,開始進行翻譯(測試),其流程就是上面寫的:輸入BOS_WORD,解碼器輸出i;輸入前面已經解碼的BOS_WORD和i,解碼器輸出am...,輸入已經解碼的BOS_WORD、i、am、a和student,解碼器輸出解碼結束標志位EOS_WORD,每次解碼都會利用前面已經解碼輸出的所有單詞嵌入信息,這個測試過程是沒有問題,但是訓練時候我肯定不想采用上述順序解碼類似rnn即一個一個目標單詞嵌入向量順序輸入訓練,肯定想采用類似編碼器中的矩陣并行算法,一步就把所有目標單詞預測出來。要實現這個功能就可以參考編碼器的操作,把目標單詞嵌入向量組成矩陣一次輸入即可,但是在解碼am時候,不能利用到后面單詞a和student的目標單詞嵌入向量信息,否則這就是作弊(測試時候不可能能未卜先知)。為此引入mask,目的是構成下三角矩陣,右上角全部設置為負無窮(相當于忽略),從而實現當解碼第一個字的時候,第一個字只能與第一個字計算相關性,當解出第二個字的時候,只能計算出第二個字與第一個字和第二個字的相關性。具體是:在解碼器中,自注意力層只被允許處理輸出序列中更靠前的那些位置,在softmax步驟前,它會把后面的位置給隱去(把它們設為-inf)。
還有個非常重要點需要知道(看圖示可以發現):解碼器內部的帶有mask的MultiHeadAttention的qkv向量輸入來自目標單詞嵌入或者前一個解碼器輸出,三者是相同的,但是后面的MultiHeadAttention的qkv向量中的kv來自最后一層編碼器的輸入,而q來自帶有mask的MultiHeadAttention模塊的輸出。
關于帶mask的注意力層寫法其實就是前面提到的代碼:
class ScaledDotProductAttention(nn.Module):
''' Scaled Dot-Product Attention '''
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
# 假設q是b,8,10,64(b是batch,8是head個數,10是樣本最大單詞長度,
# 64是每個單詞的編碼向量)
# attn輸出維度是b,8,10,10
attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
# 故mask維度也是b,8,10,10
# 忽略b,8,只關注10x10的矩陣,其是下三角矩陣,下三角位置全1,其余位置全0
if mask is not None:
# 提前算出mask,將為0的地方變成極小值-1e9,把這些位置的值設置為忽略
# 目的是避免解碼過程中利用到未來信息
attn = attn.masked_fill(mask == 0, -1e9)
# softmax+dropout
attn = self.dropout(F.softmax(attn, dim=-1))
output = torch.matmul(attn, v)
return output, attn
可視化如下:圖片來源https://zhuanlan.zhihu.com/p/44731789
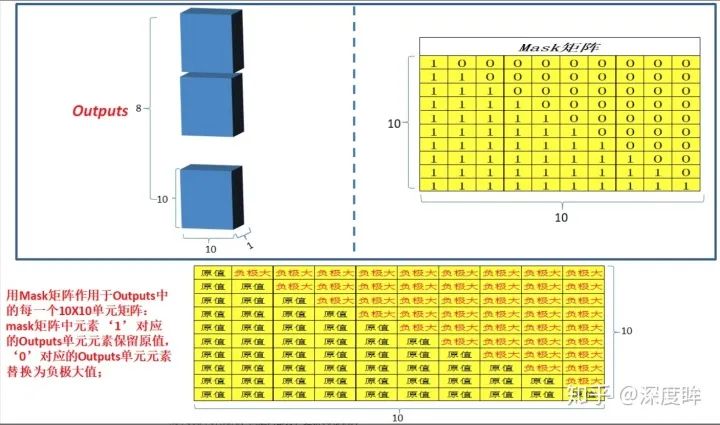
整個解碼器代碼和編碼器非常類似:
class DecoderLayer(nn.Module):
''' Compose with three layers '''
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(DecoderLayer, self).__init__()
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.enc_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
def forward(
self, dec_input, enc_output,
slf_attn_mask=None, dec_enc_attn_mask=None):
# 標準的自注意力,QKV=dec_input來自目標單詞嵌入或者前一個解碼器輸出
dec_output, dec_slf_attn = self.slf_attn(
dec_input, dec_input, dec_input, mask=slf_attn_mask)
# KV來自最后一個編碼層輸出enc_output,Q來自帶有mask的self.slf_attn輸出
dec_output, dec_enc_attn = self.enc_attn(
dec_output, enc_output, enc_output, mask=dec_enc_attn_mask)
dec_output = self.pos_ffn(dec_output)
return dec_output, dec_slf_attn, dec_enc_attn
考慮n個解碼器模塊,其整體流程為:
class Decoder(nn.Module):
def __init__(
self, n_trg_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, n_position=200, dropout=0.1):
# 目標單詞嵌入
self.trg_word_emb = nn.Embedding(n_trg_vocab, d_word_vec, padding_idx=pad_idx)
# 位置嵌入向量
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
self.dropout = nn.Dropout(p=dropout)
# n個解碼器
self.layer_stack = nn.ModuleList([
DecoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)])
# 層歸一化
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, trg_seq, trg_mask, enc_output, src_mask, return_attns=False):
# 目標單詞嵌入+位置編碼
dec_output = self.dropout(self.position_enc(self.trg_word_emb(trg_seq)))
dec_output = self.layer_norm(dec_output)
# 遍歷每個解碼器
for dec_layer in self.layer_stack:
# 需要輸入3個信息:目標單詞嵌入+位置編碼、最后一個編碼器輸出enc_output
# 和dec_enc_attn_mask,解碼時候不能看到未來單詞信息
dec_output, dec_slf_attn, dec_enc_attn = dec_layer(
dec_output, enc_output, slf_attn_mask=trg_mask, dec_enc_attn_mask=src_mask)
return dec_output
1.4.5 分類層
在進行編碼器-解碼器后輸出依然是向量,需要在后面接fc+softmax層進行分類訓練。假設當前訓練過程是翻譯任務需要輸出i am a student EOS_WORD這5個單詞。假設我們的模型是從訓練集中學習一萬個不同的英語單詞(我們模型的“輸出詞表”)。因此softmax后輸出為一萬個單元格長度的向量,每個單元格對應某一個單詞的分數,這其實就是普通多分類問題,只不過維度比較大而已。
依然以前面例子為例,假設編碼器輸出shape是(b,100,512),經過fc后變成(b,100,10000),然后對最后一個維度進行softmax操作,得到bx100個單詞的概率分布,在訓練過程中bx100個單詞是知道label的,故可以直接采用ce loss進行訓練。
self.trg_word_prj = nn.Linear(d_model, n_trg_vocab, bias=False)
dec_output, *_ = self.model.decoder(trg_seq, trg_mask, enc_output, src_mask)
return F.softmax(self.model.trg_word_prj(dec_output), dim=-1)
1.4.6 前向流程
以翻譯任務為例:
將源單詞進行嵌入,組成矩陣(加上位置編碼矩陣)輸入到n個編碼器中,輸出編碼向量KV
第一個解碼器先輸入一個BOS_WORD單詞嵌入向量,后續解碼器接受該解碼器輸出,結合KV進行第一次解碼
將第一次解碼單詞進行嵌入,聯合BOS_WORD單詞嵌入向量構成矩陣再次輸入到解碼器中進行第二次解碼,得到解碼單詞
不斷循環,每次的第一個解碼器輸入都不同,其包含了前面時間步長解碼出的所有單詞
直到輸出EOS_WORD表示解碼結束或者強制設置最大時間步長即可
這個解碼過程其實就是標準的seq2seq流程。到目前為止就描述完了整個標準transformer訓練和測試流程。
2 視覺領域的transformer
在理解了標準的transformer后,再來看視覺領域transformer就會非常簡單,因為在cv領域應用transformer時候大家都有一個共識:盡量不改動transformer結構,這樣才能和NLP領域發展對齊,所以大家理解cv里面的transformer操作是非常簡單的。
2.1 分類vision transformer
論文題目:An Image is Worth 16x16 Words:Transformers for Image Recognition at Scale
論文地址:https://arxiv.org/abs/2010.11929
github:?https://github.com/lucidrains/vit-pytorch
其做法超級簡單,只含有編碼器模塊:
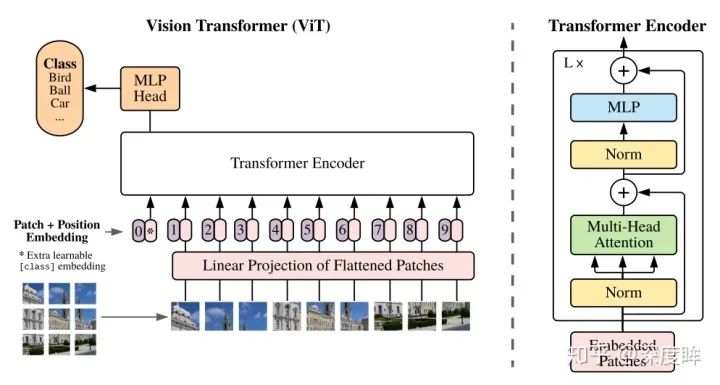
本文出發點是徹底拋棄CNN,以前的cv領域雖然引入transformer,但是或多或少都用到了cnn或者rnn,本文就比較純粹了,整個算法幾句話就說清楚了,下面直接分析。
2.1.1 圖片分塊和降維
因為transformer的輸入需要序列,所以最簡單做法就是把圖片切分為patch,然后拉成序列即可。假設輸入圖片大小是256x256,打算分成64個patch,每個patch是32x32像素
x = rearrange(img, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=p, p2=p)
這個寫法是采用了愛因斯坦表達式,具體是采用了einops庫實現,內部集成了各種算子,rearrange就是其中一個,非常高效。不懂這種語法的請自行百度。p就是patch大小,假設輸入是b,3,256,256,則rearrange操作是先變成(b,3,8x32,8x32),最后變成(b,8x8,32x32x3)即(b,64,3072),將每張圖片切分成64個小塊,每個小塊長度是32x32x3=3072,也就是說輸入長度為64的圖像序列,每個元素采用3072長度進行編碼。
考慮到3072有點大,故作者先進行降維:
# 將3072變成dim,假設是1024
self.patch_to_embedding = nn.Linear(patch_dim, dim)
x = self.patch_to_embedding(x)
仔細看論文上圖,可以發現假設切成9個塊,但是最終到transfomer輸入是10個向量,額外追加了一個0和_。為啥要追加?原因是我們現在沒有解碼器了,而是編碼后直接就進行分類預測,那么該解碼器就要負責一點點解碼器功能,那就是:需要一個類似開啟解碼標志,非常類似于標準transformer解碼器中輸入的目標嵌入向量右移一位操作。試下如果沒有額外輸入,9個塊輸入9個編碼向量輸出,那么對于分類任務而言,我應該取哪個輸出向量進行后續分類呢?選擇任何一個都說不通,所以作者追加了一個可學習嵌入向量輸入。那么額外的可學習嵌入向量為啥要設計為可學習,而不是類似nlp中采用固定的token代替?個人不負責任的猜測這應該就是圖片領域和nlp領域的差別,nlp里面每個詞其實都有具體含義,是離散的,但是圖像領域沒有這種真正意義上的離散token,有的只是一堆連續特征或者圖像像素,如果不設置為可學習,那還真不知道應該設置為啥內容比較合適,全0和全1也說不通。自此現在就是變成10個向量輸出,輸出也是10個編碼向量,然后取第0個編碼輸出進行分類預測即可。從這個角度看可以認為編碼器多了一點點解碼器功能。具體做法超級簡單,0就是位置編碼向量,_是可學習的patch嵌入向量。
# dim=1024
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
# 變成(b,64,1024)
cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)
# 額外追加token,變成b,65,1024
x = torch.cat((cls_tokens, x), dim=1)
2.1.2 位置編碼
位置編碼也是必不可少的,長度應該是1024,這里做的比較簡單,沒有采用sincos編碼,而是直接設置為可學習,效果差不多
# num_patches=64,dim=1024,+1是因為多了一個cls開啟解碼標志
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))
對訓練好的pos_embedding進行可視化,如下所示:
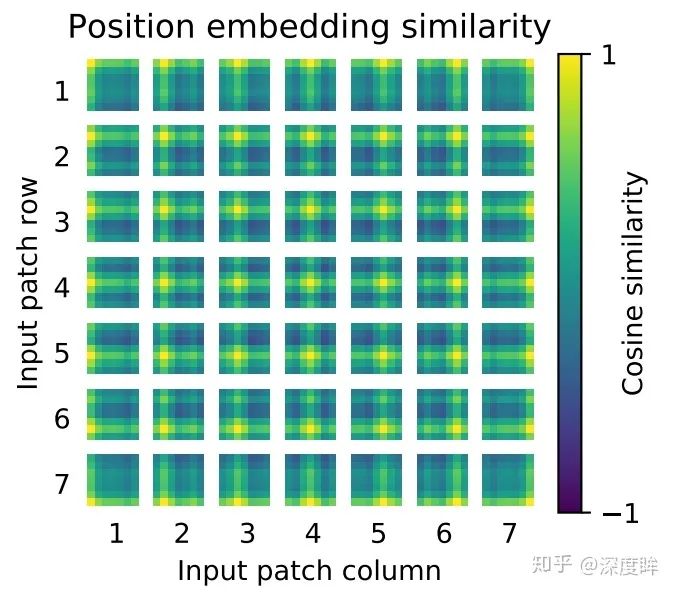
相鄰位置有相近的位置編碼向量,整體呈現2d空間位置排布一樣。
將patch嵌入向量和位置編碼向量相加即可作為編碼器輸入
x += self.pos_embedding[:, :(n + 1)]
x = self.dropout(x)
2.1.3 編碼器前向過程
作者采用的是沒有任何改動的transformer,故沒有啥說的。
self.transformer = Transformer(dim, depth, heads, mlp_dim, dropout)
假設輸入是(b,65,1024),那么transformer輸出也是(b,65,1024)
2.1.4 分類head
在編碼器后接fc分類器head即可
self.mlp_head = nn.Sequential(
nn.LayerNorm(dim),
nn.Linear(dim, mlp_dim),
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(mlp_dim, num_classes)
)
# 65個輸出里面只需要第0個輸出進行后續分類即可
self.mlp_head(x[:, 0])
到目前為止就全部寫完了,是不是非常簡單,外層整體流程為:
class ViT(nn.Module):
def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, channels=3, dropout=0.,emb_dropout=0.):
super().__init__()
# image_size輸入圖片大小 256
# patch_size 每個patch的大小 32
num_patches = (image_size // patch_size) ** 2 # 一共有多少個patch 8x8=64
patch_dim = channels * patch_size ** 2 # 3x32x32=3072
self.patch_size = patch_size # 32
# 1,64+1,1024,+1是因為token,可學習變量,不是固定編碼
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))
# 圖片維度太大了,需要先降維
self.patch_to_embedding = nn.Linear(patch_dim, dim)
# 分類輸出位置標志,否則分類輸出不知道應該取哪個位置
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
self.dropout = nn.Dropout(emb_dropout)
# 編碼器
self.transformer = Transformer(dim, depth, heads, mlp_dim, dropout)
# 輸出頭
self.mlp_head = nn.Sequential(
nn.LayerNorm(dim),
nn.Linear(dim, mlp_dim),
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(mlp_dim, num_classes)
)
def forward(self, img, mask=None):
p = self.patch_size
# 先把圖片變成64個patch,輸出shape=b,64,3072
x = rearrange(img, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=p, p2=p)
# 輸出 b,64,1024
x = self.patch_to_embedding(x)
b, n, _ = x.shape
# 輸出 b,1,1024
cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)
# 額外追加token,變成b,65,1024
x = torch.cat((cls_tokens, x), dim=1)
# 加上位置編碼1,64+1,1024
x += self.pos_embedding[:, :(n + 1)]
x = self.dropout(x)
x = self.transformer(x, mask)
# 分類head,只需要x[0]即可
# x = self.to_cls_token(x[:, 0])
x = x[:, 0]
return self.mlp_head(x)
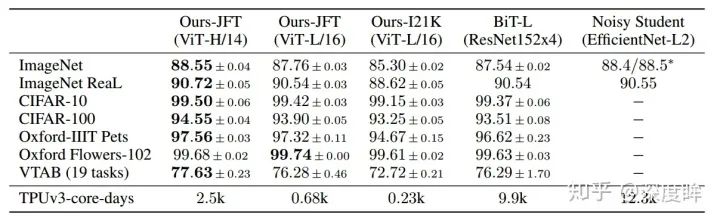
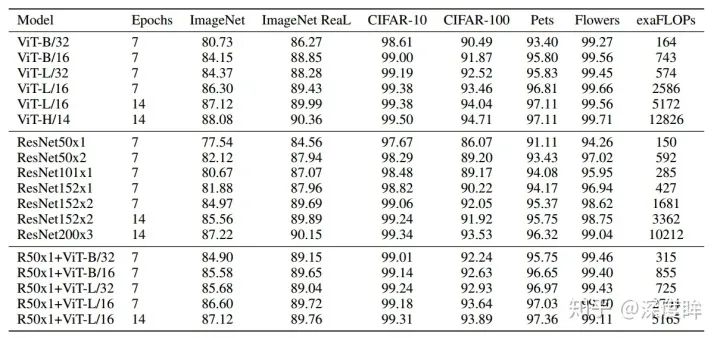
2.1.5 實驗分析
作者得出的結論是:cv領域應用transformer需要大量數據進行預訓練,在同等數據量的情況下性能不然cnn。一旦數據量上來了,對應的訓練時間也會加長很多,那么就可以輕松超越cnn。
?
同時應用transformer,一個突出優點是可解釋性比較強:

2.2 目標檢測detr
論文名稱:End-to-End Object Detection with Transformers
論文地址:https://arxiv.org/abs/2005.12872
github:https://github.com/facebookresearch/detr
detr是facebook提出的引入transformer到目標檢測領域的算法,效果很好,做法也很簡單,符合其一貫的簡潔優雅設計做法。

對于目標檢測任務,其要求輸出給定圖片中所有前景物體的類別和bbox坐標,該任務實際上是無序集合預測問題。針對該問題,detr做法非常簡單:給定一張圖片,經過CNN進行特征提取,然后變成特征序列輸入到transformer的編解碼器中,直接輸出指定長度為N的無序集合,集合中每個元素包含物體類別和坐標。其中N表示整個數據集中圖片上最多物體的數目,因為整個訓練和測試都Batch進行,如果不設置最大輸出集合數,無法進行batch訓練,如果圖片中物體不夠N個,那么就采用no object填充,表示該元素是背景。
整個思想看起來非常簡單,相比faster rcnn或者yolo算法那就簡單太多了,因為其不需要設置先驗anchor,超參幾乎沒有,也不需要nms(因為輸出的無序集合沒有重復情況),并且在代碼程度相比faster rcnn那就不知道簡單多少倍了,通過簡單修改就可以應用于全景分割任務。可以推測,如果transformer真正大規模應用于CV領域,那么對初學者來說就是福音了,理解transformer就幾乎等于理解了整個cv領域了(當然也可能是壞事)。
2.2.1 detr核心思想分析
相比faster rcnn等做法,detr最大特點是將目標檢測問題轉化為無序集合預測問題。論文中特意指出faster rcnn這種設置一大堆anchor,然后基于anchor進行分類和回歸其實屬于代理做法即不是最直接做法,目標檢測任務就是輸出無序集合,而faster rcnn等算法通過各種操作,并結合復雜后處理最終才得到無序集合屬于繞路了,而detr就比較純粹了。
盡管將transformer引入目標檢測領域可以避免上述各種問題,但是其依然存在兩個核心操作:
無序集合輸出的loss計算
針對目標檢測的transformer改進
2.2.2 detr算法實現細節
下面結合代碼和原理對其核心環節進行深入分析。
2.2.2.1 無序集合輸出的loss計算
在分析loss計算前,需要先明確N個無序集合的target構建方式。作者在coco數據集上統計,一張圖片最多標注了63個物體,所以N應該要不小于63,作者設置的是100。為啥要設置為100?有人猜測是和coco評估指標只取前100個預測結果算法指標有關系。
detr輸出是包括batchx100個無序集合,每個集合包括類別和坐標信息。對于coco數據而言,作者設置類別為91(coco類別標注索引是1-91,但是實際就標注了80個類別),加上背景一共92個類別,對于坐標分支采用4個歸一化值表征即cxcywh中心點、wh坐標,然后除以圖片寬高進行歸一化(沒有采用復雜變換策略),故每個集合是??,c是長度為92的分類向量,b是長度為4的bbox坐標向量。總之detr輸出集合包括兩個分支:分類分支shape=(b,100,92),bbox坐標分支shape=(b,100,4),對應的target也是包括分類target和bbox坐標target,如果不夠100,則采用背景填充,計算loss時候bbox分支僅僅計算有物體位置,背景集合忽略。
現在核心問題來了:輸出的bx100個檢測結果是無序的,如何和gt bbox計算loss?這就需要用到經典的雙邊匹配算法了,也就是常說的匈牙利算法,該算法廣泛應用于最優分配問題,在bottom-up人體姿態估計算法中進行分組操作時候也經常使用。detr中利用匈牙利算法先進行最優一對一匹配得到匹配索引,然后對bx100個結果進行重排就和gt bbox對應上了(對gt bbox進行重排也可以,沒啥區別),就可以算loss了。
匈牙利算法是一個標準優化算法,具體是組合優化算法,在scipy.optimize.linear_sum_assignmen函數中有實現,一行代碼就可以得到最優匹配,網上解讀也非常多,這里就不寫細節了,該函數核心是需要輸入A集合和B集合兩兩元素之間的連接權重,基于該重要性進行內部最優匹配,連接權重大的優先匹配。
上述描述優化過程可以采用如下公式表達:
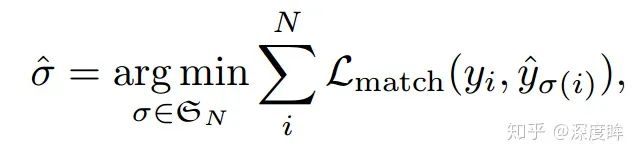
優化對象是??,其是長度為N的list,?
?,?
??表示無序gt bbox集合的哪個元素和輸出預測集合中的第i個匹配。其實簡單來說就是找到最優匹配,因為在最佳匹配情況下l_match和最小即loss最小。
前面說過匈牙利算法核心是需要提供輸入A集合和B集合兩兩元素之間的連接權重,這里就是要輸入N個輸出集合和M個gt bbox之間的關聯程度,如下所示
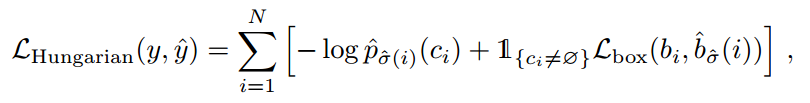
而Lbox具體是:
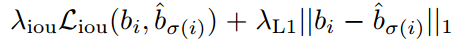
Hungarian意思就是匈牙利,也就是前面的L_match,上述意思是需要計算M個gt bbox和N個輸出集合兩兩之間的廣義距離,距離越近表示越可能是最優匹配關系,也就是兩者最密切。廣義距離的計算考慮了分類分支和bbox分支,下面結合代碼直接說明,比較簡單。
# detr分類輸出,num_queries=100,shape是(b,100,92)
bs, num_queries = outputs["pred_logits"].shape[:2]
# 得到概率輸出(bx100,92)
out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1)
# 得到bbox分支輸出(bx100,4)
out_bbox = outputs["pred_boxes"].flatten(0, 1)
# 準備分類target shape=(m,)里面存儲的是類別索引,m包括了整個batch內部的所有gt bbox
tgt_ids = torch.cat([v["labels"] for v in targets])
# 準備bbox target shape=(m,4),已經歸一化了
tgt_bbox = torch.cat([v["boxes"] for v in targets])
#核心
#bx100,92->bx100,m,對于每個預測結果,把目前gt里面有的所有類別值提取出來,其余值不需要參與匹配
#對應上述公式,類似于nll loss,但是更加簡單
cost_class = -out_prob[:, tgt_ids]
#計算out_bbox和tgt_bbox兩兩之間的l1距離 bx100,m
cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1)
#額外多計算一個giou loss bx100,m
cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox))
#得到最終的廣義距離bx100,m,距離越小越可能是最優匹配
C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
# bx100,m--> batch,100,m
C = C.view(bs, num_queries, -1).cpu()
#計算每個batch內部有多少物體,后續計算時候按照單張圖片進行匹配,沒必要batch級別匹配,徒增計算
sizes = [len(v["boxes"]) for v in targets]
#匈牙利最優匹配,返回匹配索引
indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]
在得到匹配關系后算loss就水到渠成了。分類分支計算ce loss,bbox分支計算l1 loss+giou loss
def loss_labels(self, outputs, targets, indices, num_boxes, log=True):
#shape是(b,100,92)
src_logits = outputs['pred_logits']
#得到匹配后索引,作用在label上
idx = self._get_src_permutation_idx(indices)
#得到匹配后的分類target
target_classes_o = torch.cat([t["labels"][J] for t, (_, J) in zip(targets, indices)])
#加入背景(self.num_classes),補齊bx100個
target_classes = torch.full(src_logits.shape[:2], self.num_classes,
dtype=torch.int64, device=src_logits.device)
#shape是(b,100,),存儲的是索引,不是one-hot
target_classes[idx] = target_classes_o
#計算ce loss,self.empty_weight前景和背景權重是1和0.1,克服類別不平衡
loss_ce = F.cross_entropy(src_logits.transpose(1, 2), target_classes, self.empty_weight)
losses = {'loss_ce': loss_ce}
return losses
def loss_boxes(self, outputs, targets, indices, num_boxes):
idx = self._get_src_permutation_idx(indices)
src_boxes = outputs['pred_boxes'][idx]
target_boxes = torch.cat([t['boxes'][i] for t, (_, i) in zip(targets, indices)], dim=0)
#l1 loss
loss_bbox = F.l1_loss(src_boxes, target_boxes, reduction='none')
losses = {}
losses['loss_bbox'] = loss_bbox.sum() / num_boxes
#giou loss
loss_giou = 1 - torch.diag(box_ops.generalized_box_iou(
box_ops.box_cxcywh_to_xyxy(src_boxes),
box_ops.box_cxcywh_to_xyxy(target_boxes)))
losses['loss_giou'] = loss_giou.sum() / num_boxes
return losses
2.2.2.2 針對目標檢測的transformer改進
分析完訓練最關鍵的:雙邊匹配+loss計算部分,現在需要考慮在目標檢測算法中transformer如何設計?下面按照算法的4個步驟講解。
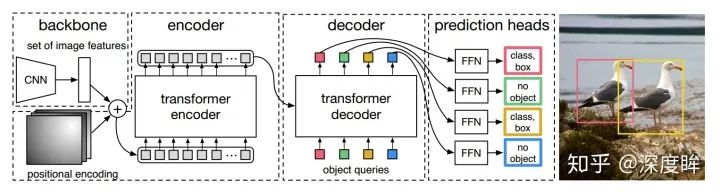
transformer細節如下:
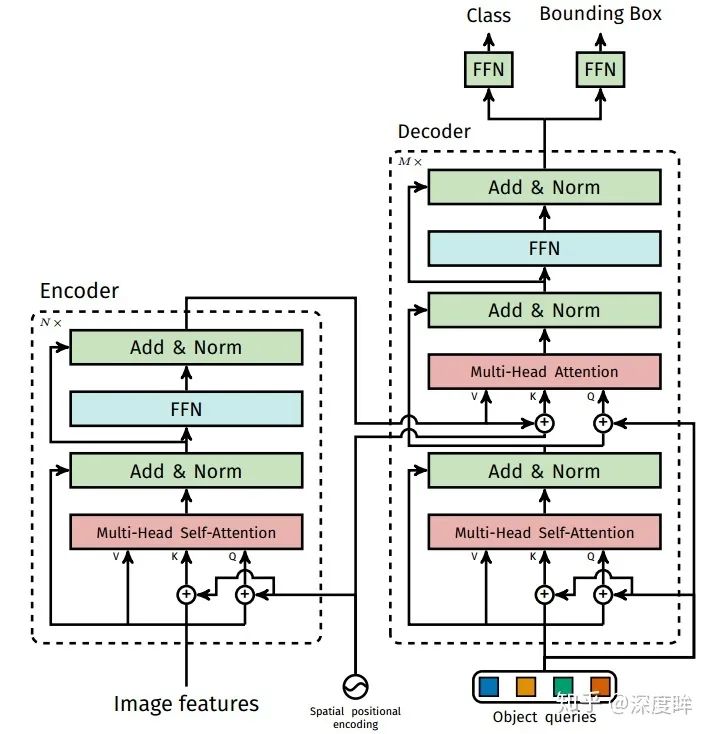
(1) cnn骨架特征提取
骨架網絡可以是任何一種,作者選擇resnet50,將最后一個stage即stride=32的特征圖作為編碼器輸入。由于resnet僅僅作為一個小部分且已經經過了imagenet預訓練,故和常規操作一樣,會進行如下操作:
resnet中所有BN都固定,即采用全局均值和方差
resnet的stem和第一個stage不進行參數更新,即parameter.requires_grad_(False)
backbone的學習率小于transformer,lr_backbone=1e-05,其余為0.0001
假設輸入是(b,c,h,w),則resnet50輸出是(b,1024,h//32,w//32),1024比較大,為了節省計算量,先采用1x1卷積降維為256,最后轉化為序列格式輸入到transformer中,輸入shape=(h'xw',b,256),h'=h//32
self.input_proj = nn.Conv2d(backbone.num_channels, hidden_dim, kernel_size=1)
# 輸出是(b,256,h//32,w//32)
src=self.input_proj(src)
# 變成序列模式,(h'xw',b,256),256是每個詞的編碼長度
src = src.flatten(2).permute(2, 0, 1)
(2) 編碼器設計和輸入
編碼器結構設計沒有任何改變,但是輸入改變了。
a) 位置編碼需要考慮2d空間
由于圖像特征是2d特征,故位置嵌入向量也需要考慮xy方向。前面說過編碼方式可以采用sincos,也可以設置為可學習,本文采用的依然是sincos模式,和前面說的一樣,但是需要考慮xy兩個方向(前面說的序列只有x方向)。
#輸入是b,c,h,w
#tensor_list的類型是NestedTensor,內部自動附加了mask,
#用于表示動態shape,是pytorch中tensor新特性https://github.com/pytorch/nestedtensor
x = tensor_list.tensors # 原始tensor數據
# 附加的mask,shape是b,h,w 全是false
mask = tensor_list.mask
not_mask = ~mask
# 因為圖像是2d的,所以位置編碼也分為x,y方向
# 1 1 1 1 .. 2 2 2 2... 3 3 3...
y_embed = not_mask.cumsum(1, dtype=torch.float32)
# 1 2 3 4 ... 1 2 3 4...
x_embed = not_mask.cumsum(2, dtype=torch.float32)
if self.normalize:
eps = 1e-6
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
# 0~127 self.num_pos_feats=128,因為前面輸入向量是256,編碼是一半sin,一半cos
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
# 歸一化
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
pos_x = x_embed[:, :, :, None] / dim_t
pos_y = y_embed[:, :, :, None] / dim_t
# 輸出shape=b,h,w,128
pos_x = torch.stack((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
# 每個特征圖的xy位置都編碼成256的向量,其中前128是y方向編碼,而128是x方向編碼
return pos # b,n=256,h,w
可以看出對于h//32,w//32的2d圖像特征,不是類似vision transoformer做法簡單的將其拉伸為h//32 x w//32,然后從0-n進行長度為256的位置編碼,而是考慮了xy方向同時編碼,每個方向各編碼128維向量,這種編碼方式更符合圖像特定。
還有一個細節需要注意:原始transformer的n個編碼器輸入中,只有第一個編碼器需要輸入位置編碼向量,但是detr里面對每個編碼器都輸入了同一個位置編碼向量,論文中沒有寫為啥要如此修改。
b) QKV處理邏輯不同
作者設置編碼器一共6個,并且位置編碼向量僅僅加到QK中,V中沒有加入位置信息,這個和原始做法不一樣,原始做法是QKV都加上了位置編碼,論文中也沒有寫為啥要如此修改。
其余地方就完全相同了,故代碼就沒必要貼了。總結下和原始transformer編碼器不同的地方:
輸入編碼器的位置編碼需要考慮2d空間位置
位置編碼向量需要加入到每個編碼器中
在編碼器內部位置編碼僅僅和QK相加,V不做任何處理
經過6個編碼器forward后,輸出shape為(h//32xw//32,b,256)。
c) 編碼器部分整體運行流程
6個編碼器整體forward流程如下:
class TransformerEncoder(nn.Module):
def __init__(self, encoder_layer, num_layers, norm=None):
super().__init__()
# 編碼器copy6份
self.layers = _get_clones(encoder_layer, num_layers)
self.num_layers = num_layers
self.norm = norm
def forward(self, src,
mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
# 內部包括6個編碼器,順序運行
# src是圖像特征輸入,shape=hxw,b,256
output = src
for layer in self.layers:
# 每個編碼器都需要加入pos位置編碼
# 第一個編碼器輸入來自圖像特征,后面的編碼器輸入來自前一個編碼器輸出
output = layer(output, src_mask=mask,
src_key_padding_mask=src_key_padding_mask, pos=pos)
return output
每個編碼器內部運行流程如下:
def forward_post(self,
src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
# 和標準做法有點不一樣,src加上位置編碼得到q和k,但是v依然還是src,
# 也就是v和qk不一樣
q = k = src+pos
src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
src = src + self.dropout1(src2)
src = self.norm1(src)
src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
src = src + self.dropout2(src2)
src = self.norm2(src)
return src
(3) 解碼器設計和輸入
解碼器結構設計沒有任何改變,但是輸入也改變了。
a) 新引入Object queries
object queries(shape是(100,256))可以簡單認為是輸出位置編碼,其作用主要是在學習過程中提供目標對象和全局圖像之間的關系,相當于全局注意力,必不可少非常關鍵。代碼形式上是可學習位置編碼矩陣。和編碼器一樣,該可學習位置編碼向量也會輸入到每一個解碼器中。我們可以嘗試通俗理解:object queries矩陣內部通過學習建模了100個物體之間的全局關系,例如房間里面的桌子旁邊(A類)一般是放椅子(B類),而不會是放一頭大象(C類),那么在推理時候就可以利用該全局注意力更好的進行解碼預測輸出。
# num_queries=100,hidden_dim=256
self.query_embed = nn.Embedding(num_queries, hidden_dim)
論文中指出object queries作用非常類似faster rcnn中的anchor,只不過這里是可學習的,不是提前設置好的。
b) 位置編碼也需要
編碼器環節采用的sincos位置編碼向量也可以考慮引入,且該位置編碼向量輸入到每個解碼器的第二個Multi-Head Attention中,后面有是否需要該位置編碼的對比實驗。
c) QKV處理邏輯不同
解碼器一共包括6個,和編碼器中QKV一樣,V不會加入位置編碼。上述說的三個操作,只要看下網絡結構圖就一目了然了。
d) 一次解碼輸出全部無序集合
和原始transformer順序解碼操作不同的是,detr一次就把N個無序框并行輸出了(因為任務是無序集合,做成順序推理有序輸出沒有很大必要)。為了說明如何實現該功能,我們需要先回憶下原始transformer的順序解碼過程:輸入BOS_WORD,解碼器輸出i;輸入前面已經解碼的BOS_WORD和i,解碼器輸出am...,輸入已經解碼的BOS_WORD、i、am、a和student,解碼器輸出解碼結束標志位EOS_WORD,每次解碼都會利用前面已經解碼輸出的所有單詞嵌入信息。現在就是一次解碼,故只需要初始化時候輸入一個全0的查詢向量A,類似于BOS_WORD作用,然后第一個解碼器接受該輸入A,解碼輸出向量作為下一個解碼器輸入,不斷推理即可,最后一層解碼輸出即為我們需要的輸出,不需要在第二個解碼器輸入時候考慮BOS_WORD和第一個解碼器輸出。
總結下和原始transformer解碼器不同的地方:
額外引入可學習的Object queries,相當于可學習anchor,提供全局注意力
編碼器采用的sincos位置編碼向量也需要輸入解碼器中,并且每個解碼器都輸入
QKV處理邏輯不同
不需要順序解碼,一次即可輸出N個無序集合
e) 解碼器整體運行流程
n個解碼器整體流程如下:
class TransformerDecoder(nn.Module):
def forward(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
# 首先query_pos是query_embed,可學習輸出位置向量shape=100,b,256
# tgt = torch.zeros_like(query_embed),用于進行一次性解碼輸出
output = tgt
# 存儲每個解碼器輸出,后面中繼監督需要
intermediate = []
# 編碼每個解碼器
for layer in self.layers:
# 每個解碼器都需要輸入query_pos和pos
# memory是最后一個編碼器輸出
# 每個解碼器都接受output作為輸入,然后輸出新的output
output = layer(output, memory, tgt_mask=tgt_mask,
memory_mask=memory_mask,
tgt_key_padding_mask=tgt_key_padding_mask,
memory_key_padding_mask=memory_key_padding_mask,
pos=pos, query_pos=query_pos)
if self.return_intermediate:
intermediate.append(self.norm(output))
if self.return_intermediate:
return torch.stack(intermediate) # 6個輸出都返回
return output.unsqueeze(0)
內部每個解碼器運行流程為:
def forward_post(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
# query_pos首先是可學習的,其作用主要是在學習過程中提供目標對象和全局圖像之間的關系
# 這個相當于全局注意力輸入,是非常關鍵的
# query_pos是解碼器特有
q = k = tgt+query_pos
# 第一個自注意力模塊
tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
tgt = tgt + self.dropout1(tgt2)
tgt = self.norm1(tgt)
# memory是最后一個編碼器輸出,pos是和編碼器輸入中完全相同的sincos位置嵌入向量
# 輸入參數是最核心細節,query是tgt+query_pos,而key是memory+pos
# v直接用memory
tgt2 = self.multihead_attn(query=tgt+query_pos,
key=memory+pos,
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
tgt = tgt + self.dropout2(tgt2)
tgt = self.norm2(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
tgt = tgt + self.dropout3(tgt2)
tgt = self.norm3(tgt)
return tgt
解碼器最終輸出shape是(6,b,100,256),6是指6個解碼器的輸出。
(4) 分類和回歸head
在解碼器輸出基礎上構建分類和bbox回歸head即可輸出檢測結果,比較簡單:
self.class_embed = nn.Linear(256, 92)
self.bbox_embed = MLP(256, 256, 4, 3)
# hs是(6,b,100,256),outputs_class輸出(6,b,100,92),表示6個分類分支
outputs_class = self.class_embed(hs)
# 輸出(6,b,100,4),表示6個bbox坐標回歸分支
outputs_coord = self.bbox_embed(hs).sigmoid()
# 取最后一個解碼器輸出即可,分類輸出(b,100,92),bbox回歸輸出(b,100,4)
out = {'pred_logits': outputs_class[-1], 'pred_boxes': outputs_coord[-1]}
if self.aux_loss:
# 除了最后一個輸出外,其余編碼器輸出都算輔助loss
out['aux_outputs'] = self._set_aux_loss(outputs_class, outputs_coord)
作者實驗發現,如果對解碼器的每個輸出都加入輔助的分類和回歸loss,可以提升性能,故作者除了對最后一個編碼層的輸出進行Loss監督外,還對其余5個編碼器采用了同樣的loss監督,只不過權重設置低一點而已。
(5) 整體推理流程
基于transformer的detr算法,作者特意強調其突出優點是部署代碼不超過50行,簡單至極。

當然上面是簡化代碼,和實際代碼不一樣。具體流程是:
將(b,3,800,1200)圖片輸入到resnet50中進行特征提取,輸出shape=(b,1024,25,38)
通過1x1卷積降維,變成(b,256,25,38)
利用sincos函數計算位置編碼
將圖像特征和位置編碼向量相加,作為編碼器輸入,輸出編碼后的向量,shape不變
初始化全0的(100,b,256)的輸出嵌入向量,結合位置編碼向量和query_embed,進行解碼輸出,解碼器輸出shape為(6,b,100,256)
將最后一個解碼器輸出輸入到分類和回歸head中,得到100個無序集合
對100個無序集合進行后處理,主要是提取前景類別和對應的bbox坐標,乘上(800,1200)即可得到最終坐標,后處理代碼如下:
prob = F.softmax(out_logits, -1)
scores, labels = prob[..., :-1].max(-1)
# convert to [x0, y0, x1, y1] format
boxes = box_ops.box_cxcywh_to_xyxy(out_bbox)
# and from relative [0, 1] to absolute [0, height] coordinates
img_h, img_w = target_sizes.unbind(1)
scale_fct = torch.stack([img_w, img_h, img_w, img_h], dim=1)
boxes = boxes * scale_fct[:, None, :]
results = [{'scores': s, 'labels': l, 'boxes': b} for s, l, b in zip(scores, labels, boxes)]
既然訓練時候對6個解碼器輸出都進行了loss監督,那么在測試時候也可以考慮將6個解碼器的分類和回歸分支輸出結果進行nms合并,稍微有點性能提升。
2.2.3 實驗分析
(1) 性能對比
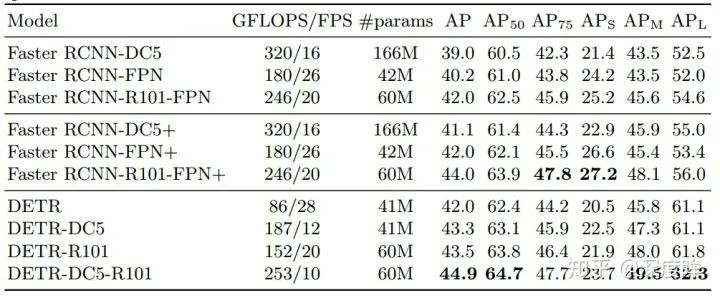
Faster RCNN-DC5是指的resnet的最后一個stage采用空洞率=stride設置代替stride,目的是在不進行下采樣基礎上擴大感受野,輸出特征圖分辨率保持不變。+號代表采用了額外的技巧提升性能例如giou、多尺度訓練和9xepoch訓練策略。可以發現detr效果稍微好于faster rcnn各種版本,證明了視覺transformer的潛力。但是可以發現其小物體檢測能力遠遠低于faster rcnn,這是一個比較大的弊端。
(2) 各個模塊分析
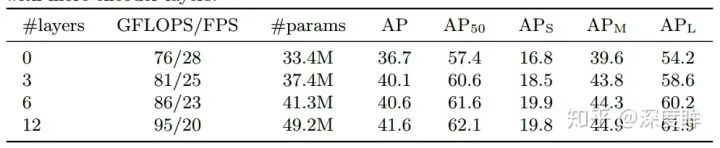
編碼器數目越多效果越好,但是計算量也會增加很多,作者最終選擇的是6。
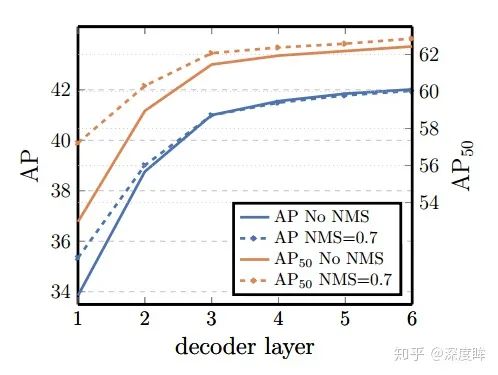
可以發現解碼器也是越多越好,還可以觀察到第一個解碼器輸出預測效果比較差,增加第二個解碼器后性能提升非常多。上圖中的NMS操作是指既然我們每個解碼層都可以輸入無序集合,那么將所有解碼器無序集合全部保留,然后進行nms得到最終輸出,可以發現性能稍微有提升,特別是AP50。
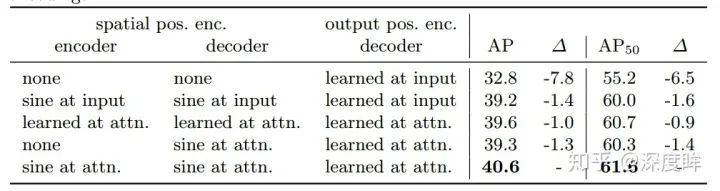
作者對比了不同類型的位置編碼效果,因為query_embed(output pos)是必不可少的,所以該列沒有進行對比實驗,始終都有,最后一行效果最好,所以作者采用的就是該方案,sine at attn表示每個注意力層都加入了sine位置編碼,相比僅僅在input增加位置編碼效果更好。
(3) 注意力可視化
前面說過transformer具有很好的可解釋性,故在訓練完成后最終提出了幾種可視化形式
a) bbox輸出可視化

這個就比較簡單了,直接對預測進行后處理即可
probas = outputs['pred_logits'].softmax(-1)[0, :, :-1]
# 只保留概率大于0.9的bbox
keep = probas.max(-1).values > 0.9
# 還原到原圖,然后繪制即可
bboxes_scaled = rescale_bboxes(outputs['pred_boxes'][0, keep], im.size)
plot_results(im, probas[keep], bboxes_scaled)
b) 解碼器自注意力層權重可視化

這里指的是最后一個解碼器內部的第一個MultiheadAttention的自注意力權重,其實就是QK相似性計算后然后softmax后的輸出可視化,具體是:
# multihead_attn注冊前向hook,output[1]指的就是softmax后輸出
model.transformer.decoder.layers[-1].multihead_attn.register_forward_hook(
lambda self, input, output: dec_attn_weights.append(output[1])
)
# 假設輸入是(1,3,800,1066)
outputs = model(img)
# 那么dec_attn_weights是(1,100,850=800//32x1066//32)
# 這個就是QK相似性計算后然后softmax后的輸出,即自注意力權重
dec_attn_weights = dec_attn_weights[0]
# 如果想看哪個bbox的權重,則輸入idx即可
dec_attn_weights[0, idx].view(800//32, 1066//32)
c) 編碼器自注意力層權重可視化

這個和解碼器操作完全相同。
model.transformer.encoder.layers[-1].self_attn.register_forward_hook(
lambda self, input, output: enc_attn_weights.append(output[1])
)
outputs = model(img)
# 最后一個編碼器中的自注意力模塊權重輸出(b,h//32xw//32,h//32xw//32),其實就是qk計算然后softmax后的值即(1,25x34=850,850)
enc_attn_weights = enc_attn_weights[0]
# 變成(25, 34, 25, 34)
sattn = enc_attn_weights[0].reshape(shape + shape)
# 想看哪個特征點位置的注意力
idxs = [(200, 200), (280, 400), (200, 600), (440, 800), ]
for idx_o, ax in zip(idxs, axs):
# 轉化到特征圖尺度
idx = (idx_o[0] // fact, idx_o[1] // fact)
# 直接sattn[..., idx[0], idx[1]]即可
ax.imshow(sattn[..., idx[0], idx[1]], cmap='cividis', interpolation='nearest')
2.2.4 小結
detr整體做法非常簡單,基本上沒有改動原始transformer結構,其顯著優點是:不需要設置啥先驗,超參也比較少,訓練和部署代碼相比faster rcnn算法簡單很多,理解上也比較簡單。但是其缺點是:改了編解碼器的輸入,在論文中也沒有解釋為啥要如此設計,而且很多操作都是實驗對比才確定的,比較迷。算法層面訓練epoch次數遠遠大于faster rcnn(300epoch),在同等epoch下明顯性能不如faster rcnn,而且訓練占用內存也大于faster rcnn。
整體而言,雖然效果不錯,但是整個做法還是顯得比較原始,很多地方感覺是嘗試后得到的做法,沒有很好的解釋性,而且最大問題是訓練epoch非常大和內存占用比較多,對應的就是收斂慢,期待后續作品。
3 總結
本文從transformer發展歷程入手,并且深入介紹了transformer思想和實現細節;最后結合計算機視覺領域的幾篇有典型代表文章進行深入分析,希望能夠給cv領域想快速理解transformer的初學者一點點幫助。
4 參考資料
1 http://jalammar.github.io/illustrated-transformer/
2 https://zhuanlan.zhihu.com/p/54356280
3 https://zhuanlan.zhihu.com/p/44731789
4 https://looperxx.github.io/CS224n-2019-08-Machine%20Translation,%20Sequence-to-sequence%20and%20Attention/
5 https://github.com/lucidrains/vit-pytorch
6 https://github.com/jadore801120/attention-is-all-you-need-pytorch
7 https://github.com/facebookresearch/detr
編輯:黃飛
?
 電子發燒友App
電子發燒友App



























評論