?
1、什么是深度學習
1.1 機器學習?

? ?
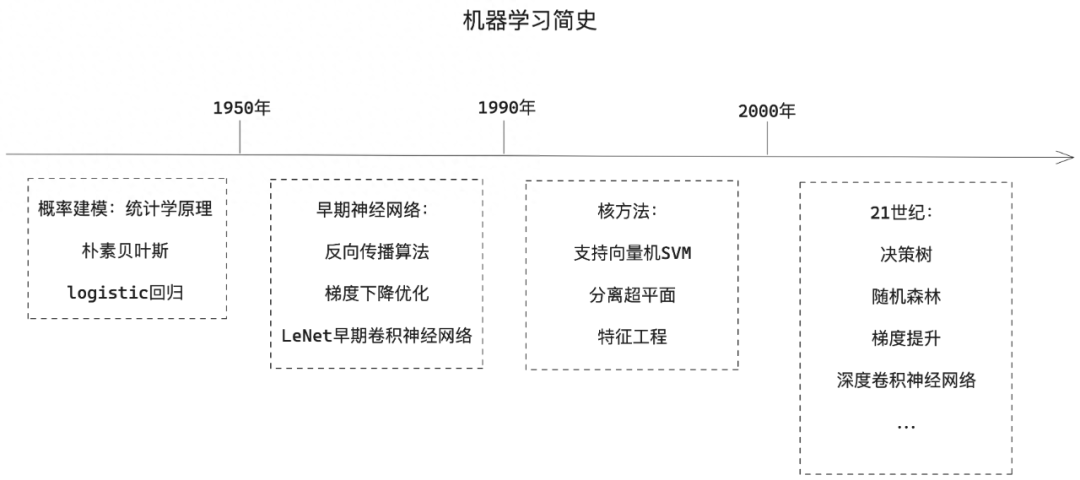
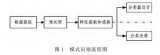
圖1:計算機有效工作的常用方法:程序員編寫規則(程序),計算機遵循這些規則將輸入數據轉換為適當的答案。這一方法被稱為符號主義人工智能,適合用來解決定義明確的邏輯問題,比如早期的PC小游戲:五子棋等,但是像圖像分類、語音識別或自然語言翻譯等更復雜、更模糊的任務,難以給出明確的規則。
圖2:機器學習把這個過程反了過來:機器讀取輸入數據和相應的答案,然后找出應有的規則。機器學習系統是訓練出來的,而不是明確的用程序編寫出來。舉個例子,如果你想為度假照片添加標簽,并希望將這項任務自動化,那么你可以將許多人工打好標簽的照片輸人機器學習系統,系統將學會把特定照片與特定標簽聯系在一起的統計規則。
定義:機器學習就是在預定義的可能性空間中,利用反饋信號的指引,在輸入數據中尋找有用的表示和規則。?
1.2 深度學習
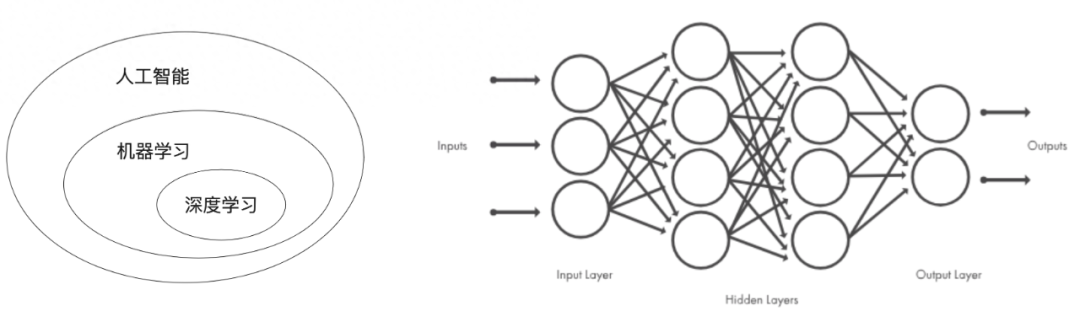
深度學習是機器學習的一個分支領域,強調從一系列連續的表示層中學習。現代的深度學習模型通常包含數十個甚至上百個連續的表示層,它們都是從訓練數據中自動學習而來。與之對應,機器學習有時也被稱為淺層學習。
在深度學習中,這些分層表示是通過叫作神經網絡的模型學習得到的。深度神經網絡可以看作多級信息蒸餾過程:信息穿過連續的過濾器,其純度越來越高。
技術定義:一種多層的學習數據表示的方法。?
??1.3 深度學習工作原理
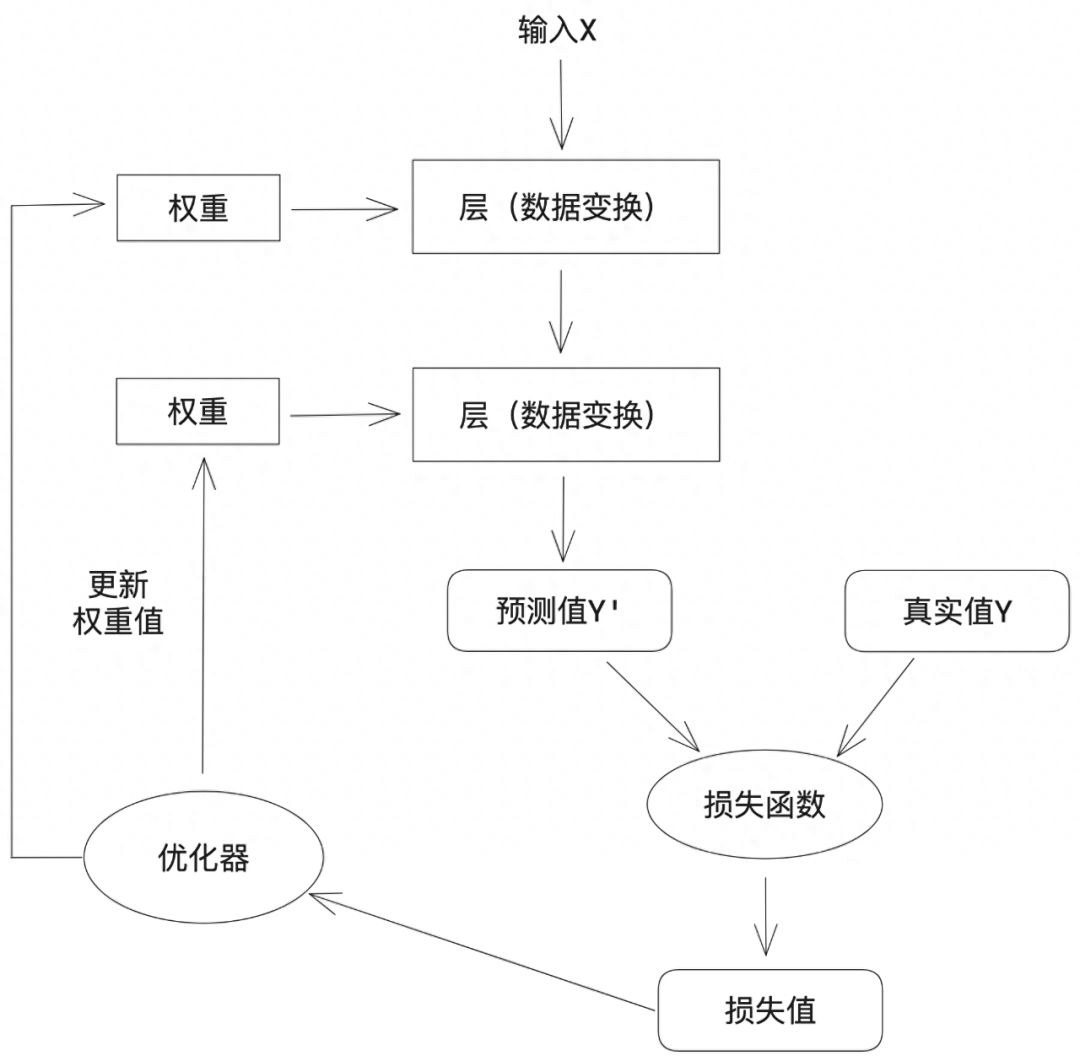
a. 對神經網絡的權重(有時也被稱為該層的參數)進行隨機賦值
b. 經過一系列隨機變換,得到預測值Y'
c. 通過損失函數(有時也被稱為目標函數或代價函數),得到預測值Y'與真實值Y之間的損失值
d. 將損失值作為反饋信號,通過優化器來對權重值進行微調,以降低當前示例對應的損失值
e. 循環重復足夠做的次數(b-d),得到具有最小損失值的神經網絡,就是一個訓練好的神經網絡?
?
2、神經網絡數學基礎
2.1 神經網絡的數據表示
目前所有機器學習系統都使用張量(tensor)作為基本數據結構,張量對這個領域非常重要,TensorFlow就是以它來命名。
張量這一概念的核心在于,它是一個數據容器。它包含的數據通常是數值數據,因此它是一個數字容器。你可能對矩陣很熟悉,它是2階張量。張量是矩陣向任意維度的推廣,張量的維度通常叫做軸。
張量是由以下3個關鍵屬性來定義的。
?軸:軸的個數
?形狀:表示張量沿每個軸的維度大小(元素個數)
?數據類型(dtype):數據的類型,可以是float16、float32、float64、unit8、string等
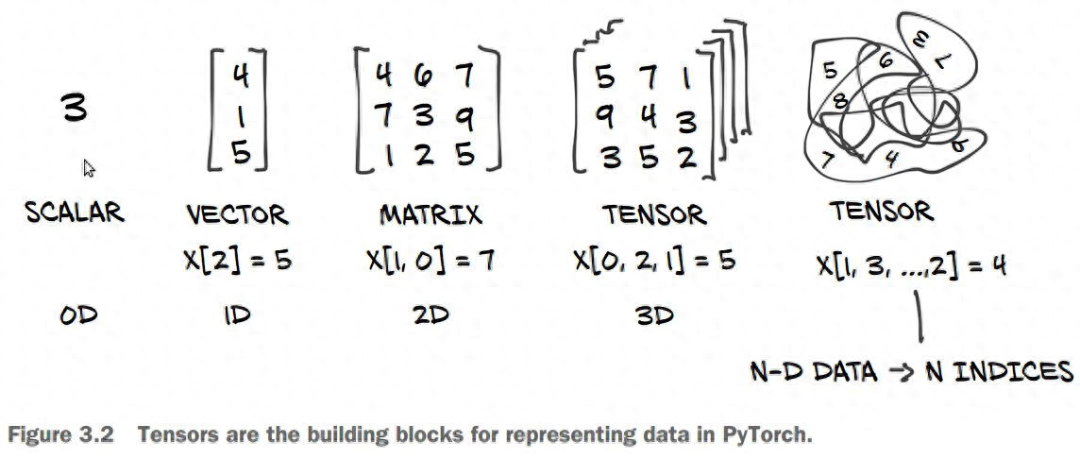
2.1.1 標量(0階張量)
僅包含一個數字的張量叫做標量(SCALAR),也叫0階張量或0維張量。
下面是一個NumPy標量
import numpy as np x = np.array(3) x.ndim // 軸:0, 形狀:()
2.1.2 向量(1階張量)
數字組成的數組叫做向量(VECTOR),也叫1階張量或1維張量。
下面是一個NumPy向量
x = np.array([4, 1, 5]) x.ndim // 軸:1, 形狀:(3,)
這個向量包含3個元素,所以也叫3維向量。不要把3維向量和3維張量混為一談,3維向量只有一個軸,沿著這個軸有3個維度。
2.1.3 矩陣(2階張量)
向量組成的數組叫做矩陣(MATRIX),也2階張量或2維張量。矩陣有2個軸:行和列。
下面是一個NumPy矩陣
x = np.array([
[4, 6, 7],
[7, 3, 9],
[1, 2, 5]
])
x.ndim // 軸:2, 形狀:(3, 3)
現實世界中的向量實例:
向量數據:形狀為(samples, features)的2階張量,每個樣本都是一個數值(特征)向量,向量數據庫存儲的基本單位。
2.1.4 3階張量與更高階的張量
將多個矩陣打包成一個新的數組,就可以得到一個3階張量(或3維張量)
下面是一個3階NumPy張量
x = np.array([
[[4, 6, 7],
[7, 3, 9],
[1, 2, 5]],
[[5, 7, 1],
[9, 4, 3],
[3, 5, 2]]
])
x.ndim // 軸:3, 形狀:(2, 3, 3)
將多個3階張量打包成一個數組,就可以創建一個4階張量。
現實世界中的實例:
時間序列數據或序列數據:形狀為(samples, timesteps, features)的3階張量,每個樣本都是特征向量組成的序列(序列長度為timesteps)
圖像數據:形狀為(samples, height, width, channels)的4階張量,每個樣本都是一個二維像素網格,每個像素則由一個“通道”(channel)向量表示。
視頻數據:形狀為(samples, frames, height, width, channels)的5階張量,每個樣本都是由圖像組成的序列(序列長度為frames)。
? ?
2.2 神經網絡的“齒輪”:張量運算
所有計算機程序最終都可以簡化為對二進制輸入的一些二進制運算,與此類似,深度神經網絡學到的所有變換也都可以簡化為對數值數據張量的一些張量運算或張量函數。
2.2.1 逐元素運算
逐元素運算,即該運算分別應用于張量的每個元素。參與運算的張量的形狀必須相同。
import numpy as np z = x + y // 逐元素加法 z = x - y // 逐元素加法 z = x * y // 逐元素乘積 z = x / y // 逐元素除法 z = np.maximum(z, 0.) //逐元素relu,大于0輸出等于輸入,小于0則輸出為0
rule運算是一種常用的激活函數,rule(x)就是max(x, 0):如果輸入x大于0,則輸出等于輸入值;如果輸入x小于等于0,則輸出為0。
2.2.2 張量積
張量積或點積是最常見且最有用的張量運算之一。注意,不要將其與逐元素乘積弄混。
在NumPy中使用np.dot函數來實現張量積:z = np.dot(x, y)
數學符號中的(·)表示點積運算:z = x · y
?兩個向量的點積是一個標量,而且只有元素個數相同的向量才能進行點積運算。
?一個矩陣x和一個向量y做點積運算,其返回值是一個向量,其中每個元素是y和x每一行的點積。
?對于矩陣x和y,當且僅當x.shape[1] == y.shape[0]時,才可以計算點積,其結果是一個形狀為(x.shape[0], y.shape[1])的矩陣,其元素是x的行與y的列之間的向量點積。
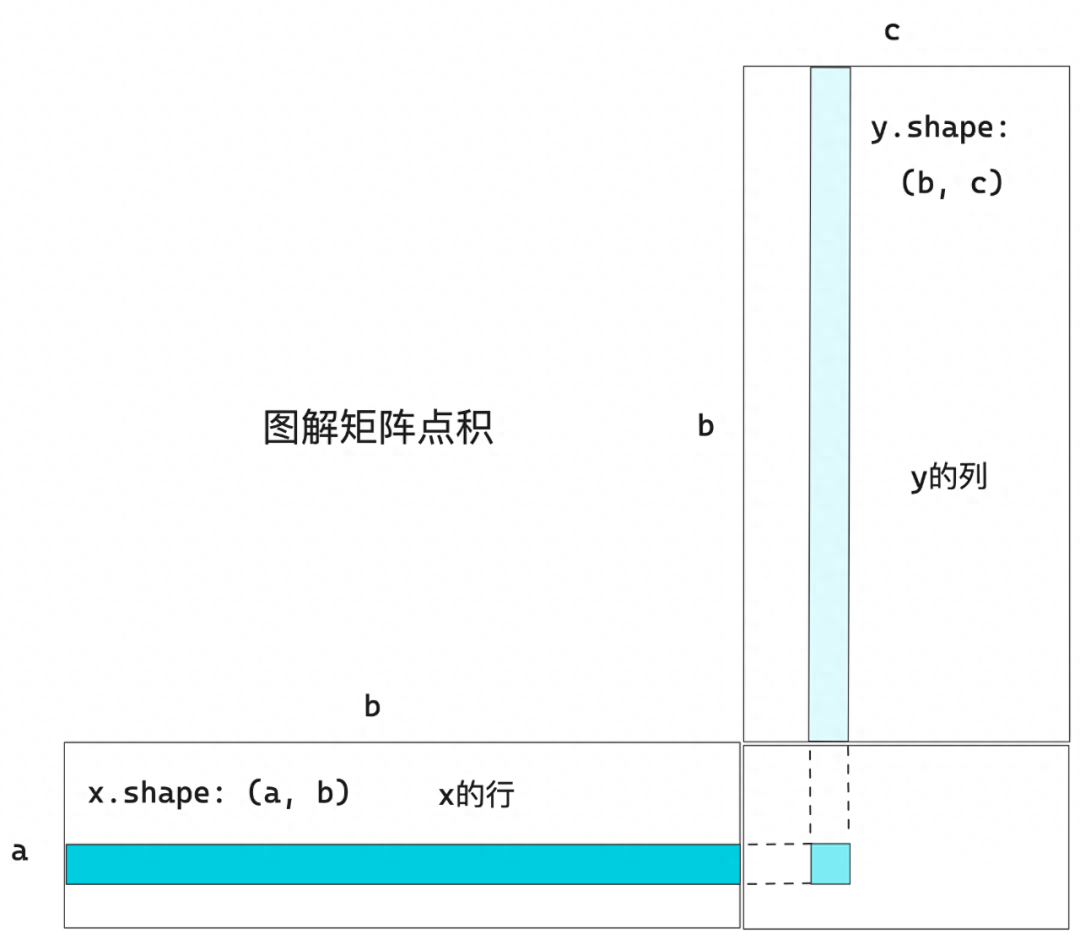
2.2.3 張量變形
張量變形是指重新排列張量的行和列,以得到想要的形狀。變形后,張量的元素個數與初始張量相同。
import numpy as np
x = np.array([[0, 1],
[2, 3]
[4, 5]])
x.shape //(3, 2)
x = x.reshape((6, 1))
>>> x
array([[0],
[1],
[2],
[3],
[4],
[5]])
x = x.reshape(2, 3)
>>> x
array([[0, 1, 2],
[3, 4, 5]])
常見的一種特殊的張量變形是轉置。矩陣轉置是指將矩陣的行和列互換,即x[i, :]變為x[:, i]
x = np.zeros((300, 20)) //創建一個形狀為(300, 20)的零矩陣 x = np.transpose(x) >>> x.shape (20, 300)
2.2.4 張量運算的幾何解釋
平移、旋轉、縮放、傾斜等基本的幾何操作都可以表示為張量運算。?
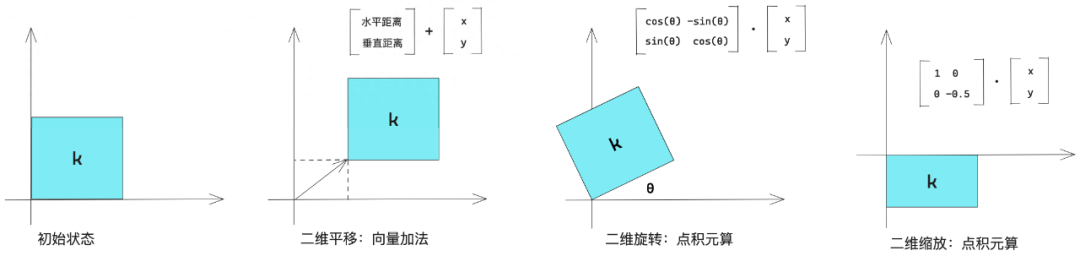
??線性變換:與任意矩陣做點積運算,都可以實現一次線性變換。縮放和旋轉,都屬于線性變換。?仿射變換:一次線性變換與一次平移的組合。?帶有rule激活函數的仿射變換:多次仿射變換相當于一次仿射變換,因此一個完全沒有激活函數的多層神經網絡等同于一層,這種“深度”神經網絡其實就是一個線性模型。?
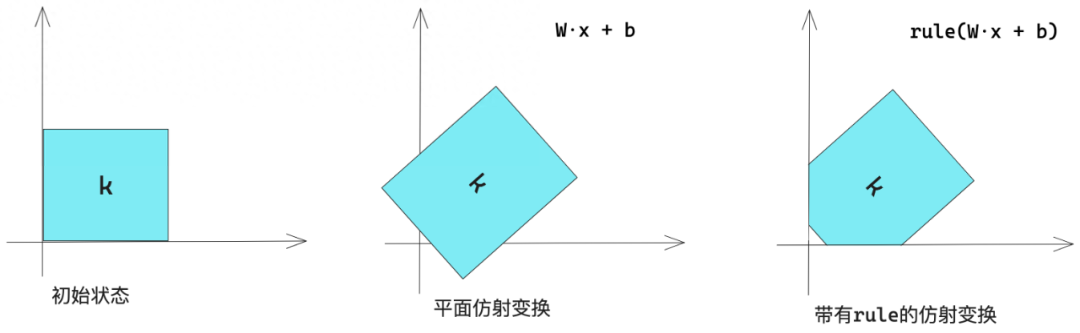
??2.2.5 深度學習的幾何解釋
神經網絡完全由一系列張量運算組成,而這些張量運算只是輸入數據的簡單幾何變換。因此,你可以將神經網絡解釋為高維空間中非常復雜的幾何變換,這種變換通過一系列簡單步驟來實現。
機器學習的目的:為高維空間中復雜、高度折疊的數據流行(一個連續的表面)找到簡潔的表示。深度學習可以將復雜的幾何變換逐步分解為一系列基本變換。
2.3 神經網絡的“引擎”:基于梯度的優化
步驟a看起來很簡單,只是輸入/輸出(I/O)的代碼。步驟b、c僅僅是應用了一些張量運算。難點在于步驟d:更新模型權重。對于模型的某個權重系數,你怎么知道這個系數應該增大還是減小,以及變化多少?
一種簡單的解決方案是,保持模型的其他權重不變,只考慮一個標量系數,讓其嘗試不同的取值。對于模型的所有系數都要重復這一過程。但這種方法非常低效,因為系數有很多(通常有上千個,甚至多達百萬個)。幸運的是,有一種更好的方法:梯度下降法。
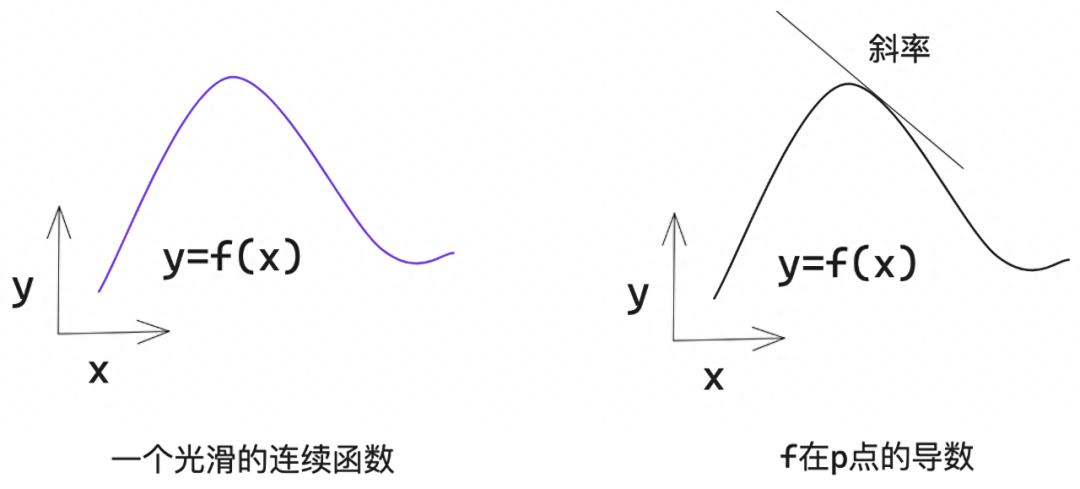
2.3.1 導數
假設有一個光滑連續的函數f(x) = y,由于函數是連續的,因此x的微小變化只會導致y的微小變化。因此在某個點p附近,如果x變化足夠小,就可以將f近似看作斜率為a的線性函數。
斜率a被稱為f在p點的導數。如果a < 0,說明x在p點附近的微增將導致f(x)減小;如果a > 0,那么x在p點附近的微增將導致f(x)增大;?
2.3.2 梯度
導數這一概念可以應用于任何函數,只要函數所對應的表面是連續且光滑的。張量運算的導數叫做梯度。對于一個標量函數來說,導數是表示函數曲線的局部斜率,張量函數的梯度表示該函數所對應多維表面的曲率。
舉例來說,物體位置相對于時間的梯度是這個物體的速度,二階梯度則是它的加速度。
2.3.3 隨機梯度下降
步驟d中更新模型權重,假設我們要處理的是一個可微函數,可以計算出它的梯度,沿著梯度的反方向更新權重,每次損失都會減小一點。
(1)抽取訓練樣本x和對應目標y_true組成的一個數據批量
(2)在x上運行模型,得到預測值y_pred(前向傳播)
(3)計算模型在這批數據上的損失值
(4)計算損失相對于模型參數的梯度(反向傳播)
(5)將參數沿著梯度的反方向移動一小步,從而減小損失值
這個方法叫做小批量隨機梯度下降(SGD),隨機是指每批數據都是隨機抽取的;如果每次迭代都在所有數據上運行,這叫做批量梯度下降,但是計算成本高得多,折中辦法是選擇合理的小批量大小。
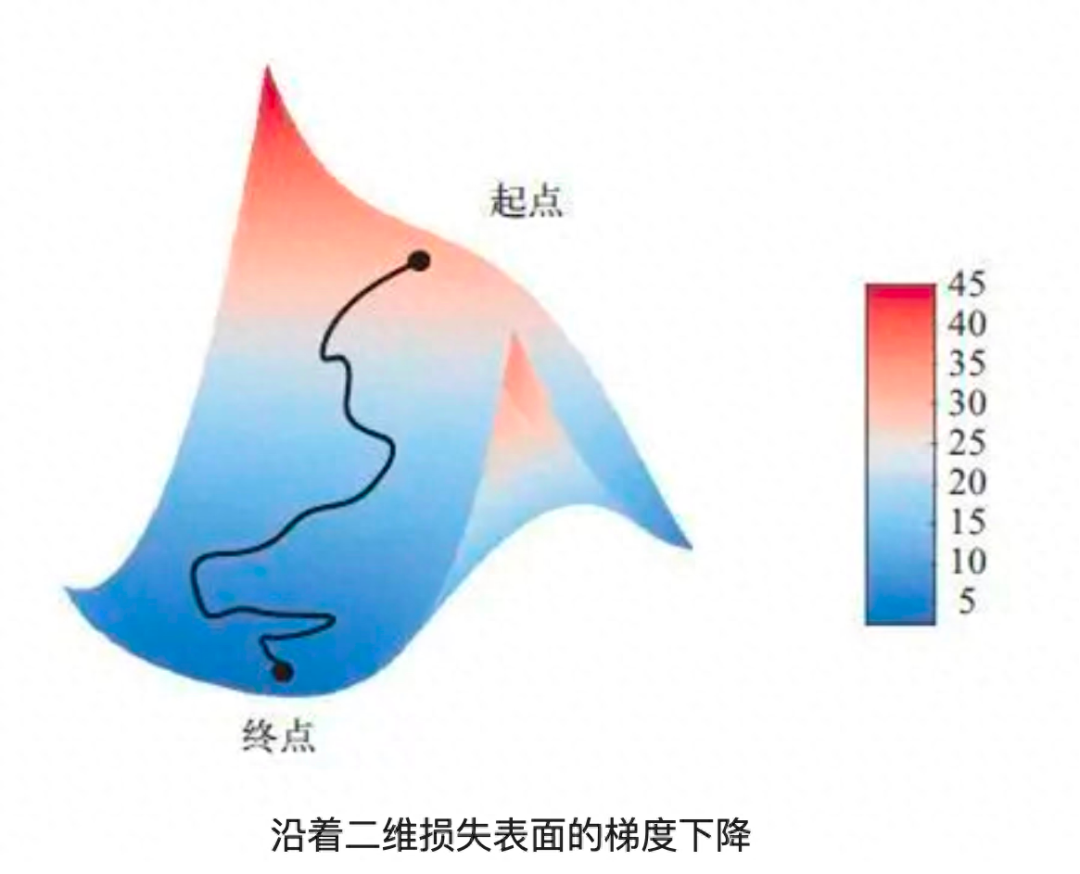
神經網絡的每一個權重系數都是空間中的一個自由維度,為了對損失表面有更直觀的認識,可以將沿著二維損失表面的梯度下降可視化,但你不可能將神經網絡的真實訓練過程可視化,因為無法用人類可以理解的方式來可視化1 000 000維空間。這些低維表示中建立的直覺,實踐中不一定總是準確的。?
??2.3.4 鏈式求導:反向傳播
在前面的算法中,我們假設函數是可微(可以被求導)的,所以很容易計算其梯度。但是在實踐中如何計算復雜表達式的梯度?這時就需要用到反向傳播算法。
(1)鏈式法則
利用簡單運算(如加法、rule或張量積)的導數,可以輕松計算出這些基本運算的任意復雜組合的梯度。鏈式法則規定:grad(y, x) == grad(y, x1) * grad(x1, x),因此只要知道f和g的導數,就可以求出fg的導數。如果添加更多的中間函數,看起來就像是一條鏈。將鏈式法則應用于神經網絡梯度值的計算,就得到了一種叫做反向傳播的算法。
(2)用計算圖進行自動微分
思考反向傳播的一種有用方法是利用計算圖。計算圖是TensorFlow和深度學習革命的核心數據結構。它是一種由運算構成的有向無環圖。如今,現代框架比如TensorFlow,支持基于計算圖的自動微分,可以計算任意可維張量運算組合的梯度,只需寫出前向傳播,而無需做任何額外工作。
GradientTape是一個API,讓你可以充分利用TensorFlow強大的自動微分能力。它是一個Python作用域,能夠以計算圖(tape)的形式記錄在其中運行的張量運算。
?
3、實踐:使用Python的Kears庫識別手寫數字
在這個例子中,我們要解決的問題是,將手寫數字的灰度圖像(28像素 * 28像素)劃分到10個類別(從0到9)中,我們將使用MNIST數據集,它是機器學習領域的一個經典數據集。你可以將解決MNIST問題看作深度學習的“Hello World”。
3.1 加載Kears中的MNIST數據集
from tensorflow.keras.datasets import mnist (train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images, train_labels組成了訓練集,模型將從這些數據中進行學習。我們會在測試集test_images, test_labels上對模型進行測試。
查看數據集形狀:
>>> train_images.shape (60000, 28, 28) //訓練集為60000張圖片,每張圖片中28*28像素點數據 >>> test_images.shape (10000, 28, 28) //測試集為10000張圖片,每張圖片中28*28像素點數據
3.2 神經網絡架構模型
from tensorflow import keras from tensorflow.keras import layers model = keras.Sequential([ layers.Dense(512, activation="relu"), layers.Dense(10, activation="softmax") ])
神經網絡的核心組件是層(layer),大多數深度學習工作設計將簡單的層鏈接起來,從而實現漸進式的數據蒸餾,從輸入數據中提取表示。
本例中的模型包含2個Dense層,每層都對輸入數據做一些簡單的張量運算(relu、softmax),這些運算都涉及權重張量,權重張量是該層的屬性或參數,里面保存了模型所學到的知識。
3.3 模型編譯
model.compile(
optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"]
)
這里指定了編譯的3個步驟:優化器、損失函數以及監控的指標。其中
sparse_categorical_crossentropy是損失函數,用于學習權重張量的反饋信號;使用rmsprop優化器,通過小批量隨機梯度下降(SGD)降低損失值。
3.4 準備圖像數據
train_images = train_images.reshape((60000, 28*28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28*28))
test_images = test_images.astype("float32") / 255
在開始訓練之前,我們先對數據進行預處理,將其變化為模型要求的形狀,并縮放到所有值都在[0, 1]區間。
3.5 擬合模型
model.fit(train_images, train_labels, epochs=5, batch_size=128)
在Keras中通過調用模型的fit方法來完成訓練數據上的擬合模型:模型開始在訓練數據上進行迭代(每個小批量包含128個樣本),共迭代5輪。對于每批數據,模型會計算損失相對于權重的梯度,并將權重沿著減小該批量對應損失值的方向移動,5輪迭代后訓練精度到達了98.9%。
3.6 利用模型預測
>>> test_digits = test_images[0:10] >>> predictions = model.predict(test_digits) >>> predictions[0] //為了方面閱讀,以下數據均為示例 array([1.07, 1.69, 6.13, 8.41, 2.99, 3.03, 8.36, 9.99, 2.66, 3.81], dtype=float32)
這個數組中的每個值,為對應數字圖像test_digits[0]屬于0-9類別的概率,可以看到第7個概率最大,因此這個數字一定是7。檢查測試標簽是否與之一致:
>>> test_lables[0] 7
3.7 在新數據上評估模型
>>> test_loss, test_acc = model.evaluate(test_images, test_lables)
>>> print(f"test_acc: {test_acc}")
test_acc: 0.9785
測試精度約為97.8%,比訓練精度98.9%低不少。訓練精度和測試精度之間的這種差距是過擬合造成的。
編輯:黃飛
?
 電子發燒友App
電子發燒友App











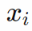













評論