本文中,我們將研究擴散模型的理論基礎,然后演示如何在PyTorch中使用擴散模型生成圖像。 ? 擴散模型的迅速崛起是機器學習在過去幾年中最大的發展之一。在這篇文章中,你能了解到關于擴散模型的一切。 ? ? ?
擴散模型是生成模型,在過去的幾年里已經獲得了顯著的普及。僅在21世紀20年代發表的幾篇開創性論文就向世界展示了擴散模型的能力,比如在圖像合成方面擊敗GANs。以及DALL-E 2,OpenAI的圖像生成模型的發布。 ? ?
? ? 鑒于擴散模型最近的成功浪潮,許多機器學習從業者肯定對它們的內部工作原理感興趣。在本文中,我們將研究擴散模型的理論基礎,然后演示如何在PyTorch中使用擴散模型生成圖像。??
介紹
擴散模型是生成模型,這意味著它們用于生成與訓練數據相似的數據。從根本上講,擴散模型的工作原理是通過連續添加高斯噪聲破壞訓練數據,然后通過學習反轉這個噪聲過程來恢復數據。訓練后,我們可以使用擴散模型通過簡單地通過學習的去噪過程傳遞隨機采樣的噪聲來生成數據。
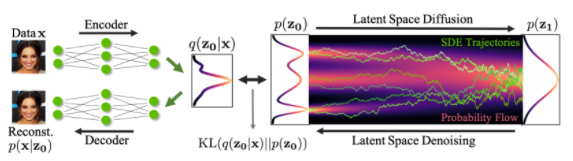
更具體地說,擴散模型是一種潛變量模型,它使用固定的馬爾可夫鏈映射到潛在空間。該鏈逐步向數據中添加噪聲,以獲得近似后驗值,其中為與x0具有相同維數的潛變量。在下面的圖中,我們可以看到這樣一個馬爾可夫鏈。

最后,圖像逐漸變為純高斯噪聲。訓練擴散模型的目標是學習逆向過程,即訓練。通過沿著這條鏈向后遍歷,我們可以生成新的數據。
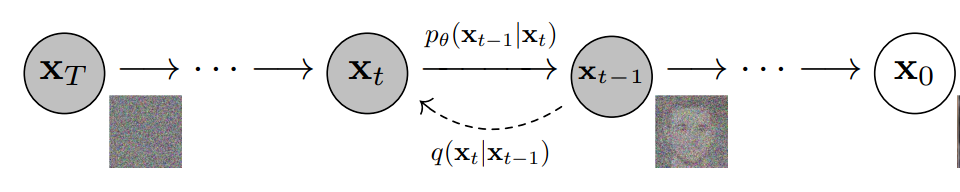
擴散模型的優點
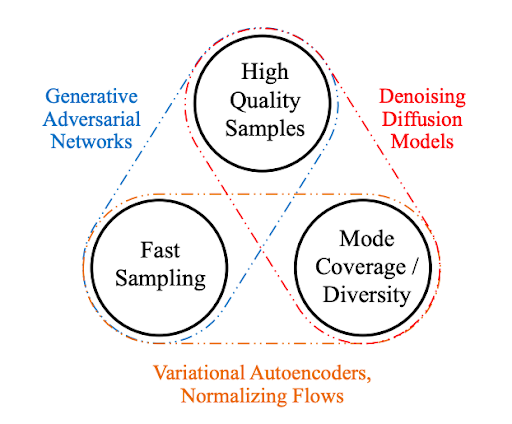
如上所述,對擴散模型的研究近年來呈爆炸式增長。受非平衡熱力學的啟發,擴散模型目前可以生成State-of-the-Art 的圖像質量。
除了頂尖的圖像質量,擴散模型還帶來了許多其他好處,包括不需要對抗性訓練。對抗訓練的困難是有據可查的。在訓練效率的話題上,擴散模型還具有可伸縮性和并行性的額外好處。
雖然擴散模型似乎是憑空產生的結果,但有很多仔細和有趣的數學選擇和細節為這些結果提供了基礎,并且最佳實踐仍在文獻中不斷發展。現在讓我們更詳細地看看支撐擴散模型的數學理論。
擴散模型——深入
如上所述,擴散模型由正向過程(或擴散過程)和反向過程(或反向擴散過程)組成,前者是對數據(通常是圖像)進行逐步噪聲化,后者是將噪聲從目標分布轉化回樣本。
當噪聲水平足夠低時,正向過程中的采樣鏈轉換可以設置為條件高斯。將這與馬爾可夫假設結合起來,就得到了正向過程的簡單參數化:
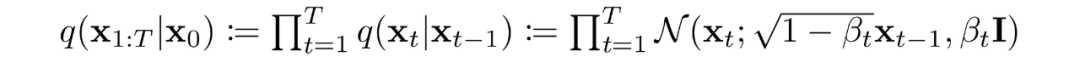
是一個方差策略(學習的或固定的),如果表現良好,確保對于足夠大的T,幾乎是一個各向同性的高斯噪聲。

在馬爾可夫假設下,潛變量的聯合分布是高斯條件鏈變換的乘積 ?
如前所述,擴散模型的“魔力”來自于反向過程。在訓練過程中,模型學習這個擴散過程的反轉,以生成新的數據。從純高斯噪聲開始,模型學習聯合分布為:
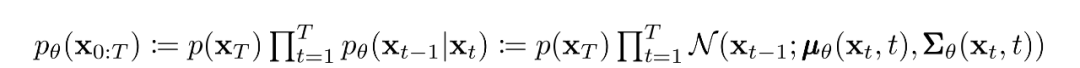
其中高斯變換的隨時間變化的參數被學習到。特別要注意的是,馬爾可夫公式斷言,給定的反向擴散變換分布只依賴于前一個時間步(或下一個時間步,取決于你如何看待它):
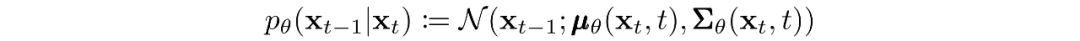
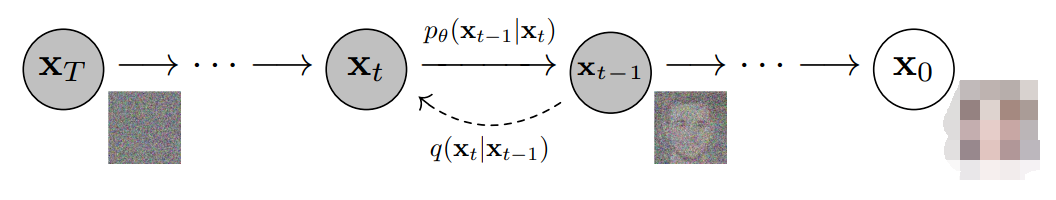
訓練
擴散模型通過尋找反向馬爾可夫變換來訓練,使訓練數據的似然性最大化。在實踐中,訓練等價于最小化負對數似然的變分上界。
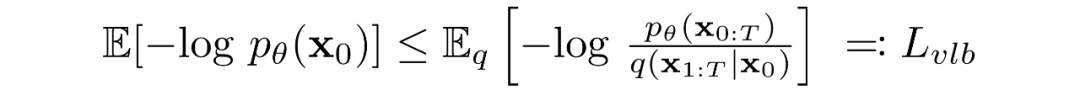
我們試圖根據?Kullback-Leibler (KL) Divergences?重寫。KL 散度是一種不對稱統計距離度量,衡量一個概率分布 P 與參考分布 Q 的差異程度。我們感興趣的是根據 KL 散度來重寫,因為我們的馬爾可夫鏈中的過渡分布是高斯分布,并且高斯分布之間的 KL散度具有封閉形式。
什么是KL散度?
連續分布的KL散度的數學形式:
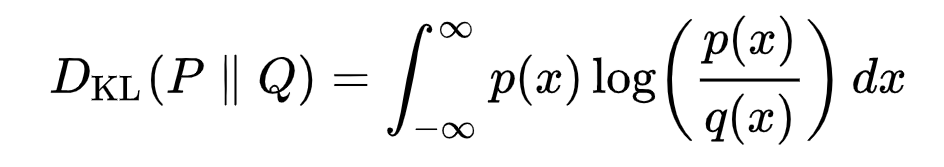
雙杠表示該函數關于其參數不對稱
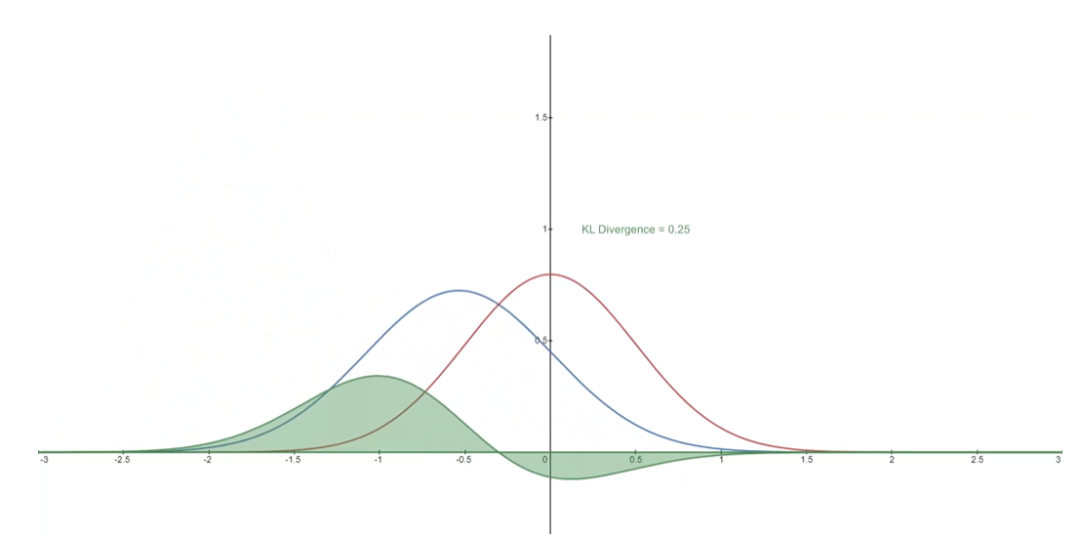
下面你可以看到分布 P(藍色)與參考分布 Q(紅色)的 KL 散度的變化。綠色曲線表示上述KL散度定義中積分內的函數,曲線下的總面積表示任意給定時刻P與Q的KL散度值。
將轉換為KL散度的形式
如上所述,可以將重寫成KL散度的形式:
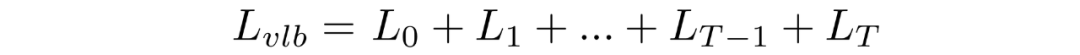
其中
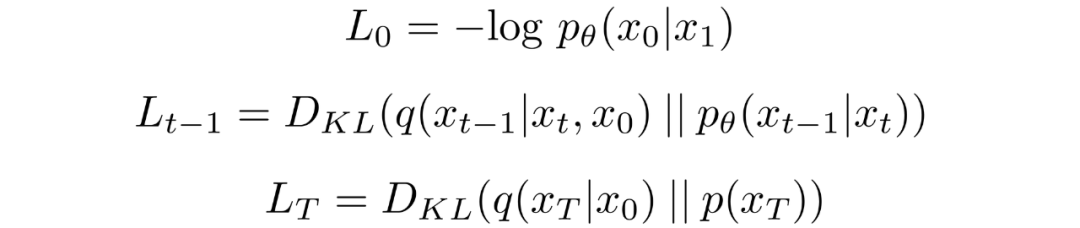
對中的后驗的前向過程進行條件化會導致易于處理的形式,從而導致所有 KL 散度都是高斯分布之間的比較。這意味著可以使用封閉式表達式而不是蒙特卡羅估計來精確計算。
模型選擇
建立了目標函數的數學基礎后,我們現在需要就如何實施擴散模型做出幾個選擇。對于前向過程,唯一需要的是定義方差策略,其值在前向過程中通常會增加。
對于逆向過程,我們多選擇高斯分布參數化/模型架構。請注意擴散模型提供的高度靈活性——我們架構的唯一要求是其輸入和輸出具有相同的維度。
我們將在下面更詳細地探討這些選擇的細節。
前向過程和
如上所述,關于前向過程,我們必須定義方差策略。特別是,我們將它們設置為依賴時間的常數,而忽略了它們可以學習的事實。例如,從到可能使用線性策略,或者可能使用幾何級數。
不管選擇的特定值如何,方差策略是固定的這一事實導致了相對于我們的可學習參數集成為了一個常數,允許我們就訓練而言忽略它。
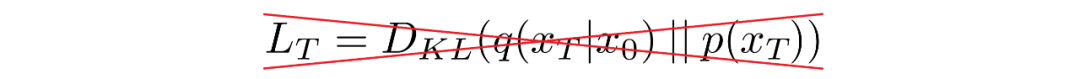
反向過程和
現在我們討論定義反向向過程所需的東西。回想一下,我們將逆馬爾可夫轉換定義為高斯:
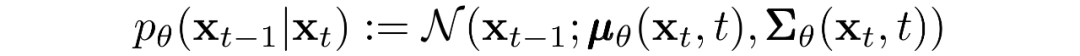
我們現在必須定義?或的函數形式。雖然有更復雜的方法來參數化,我們只需設置:
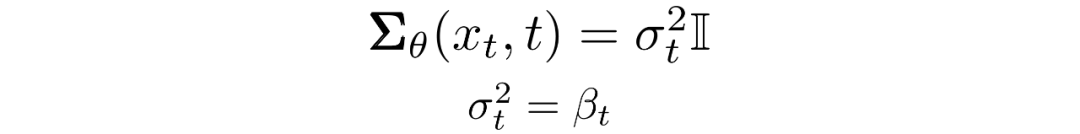
也就是說,我們假設多元高斯分布是具有相同方差的獨立高斯分布的乘積,方差值可以隨時間變化。我們將這些方差設置為我們的前向過程中的方差策略中的值。
給定了新的的形式,我們有:
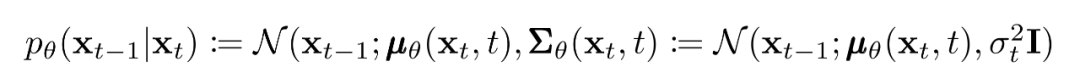
這就允許我們進行變換,將:
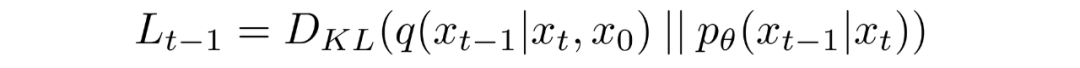
變換為:
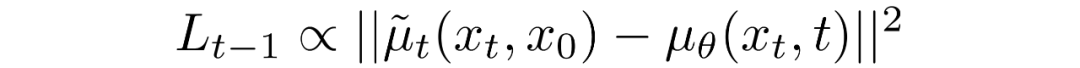
其中差分中的第一項是和的線性組合,它取決于方差策略。此函數的確切形式與我們的目的無關。
上述比例的意義在于最直接的對進行參數化,直接預測擴散的后驗均值。重要的是,有學者發現訓練來預測噪聲,在任何給定時間步長的下都會產生更好的結果。特別地,讓
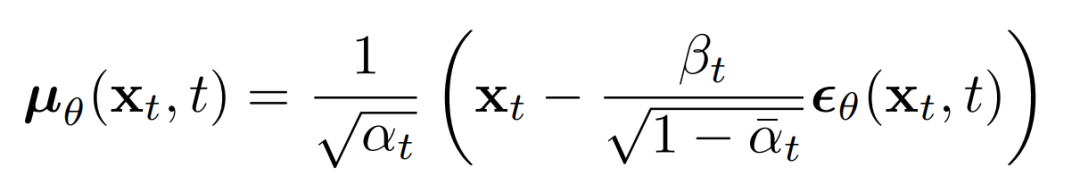
這里:
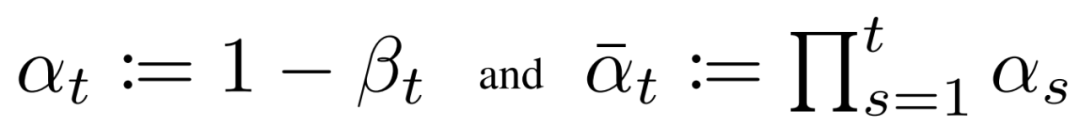
這可以導出下面的替代損失函數,有學者發現可以帶來更穩定的訓練和更好的結果:
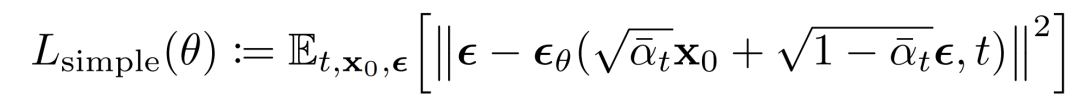
img
該學者還注意到這種擴散模型公式與得分匹配生成模型在基于Langevin 動力學的模型上的聯系 。事實上,擴散模型和基于分數的模型似乎是同一枚硬幣的兩面,類似于基于波的量子力學和基于矩陣的量子力學的獨立和同時發展,揭示了同一現象的兩個等價公式。
網絡結構
雖然我們的簡化損失函數旨在訓練模型,但我們仍未定義該模型的架構。請注意,模型的唯一要求是其輸入和輸出維度相同。
鑒于此限制,圖像擴散模型通常使用類似 U-Net 的架構來實現。
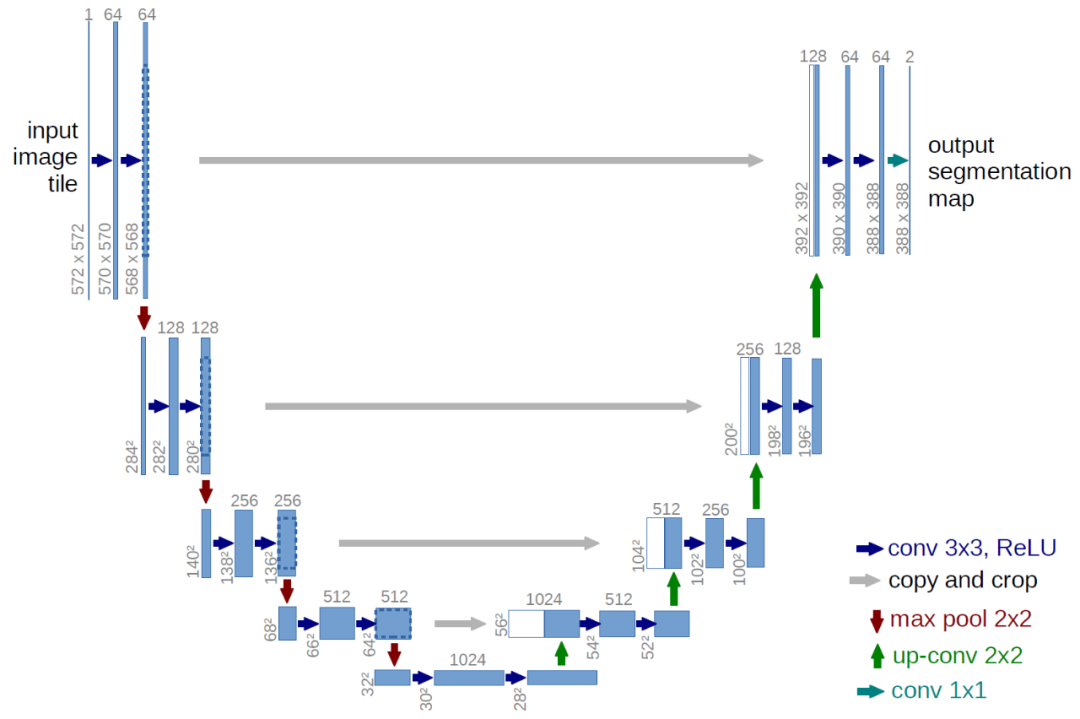
反向過程解碼和
反向過程的路徑由連續條件高斯分布下的許多變換組成。在反向過程結束時,回想一下我們正在嘗試生成一個圖像,它由整數像素值組成。因此,我們必須設計一種方法來獲得所有像素中每個可能像素值的離散(對數)似然。
這樣做的方法是將反向擴散鏈中的最后一個轉換設置為獨立的離散解碼器。為了確定給定生成圖像的可能性,我們首先在數據維度之間施加獨立性:

其中D為數據的維數,上標i表示取一個坐標。現在的目標是在時刻t=1時,一個給定的像素的概率分布和輕微噪聲圖中的對應像素的相似程度:
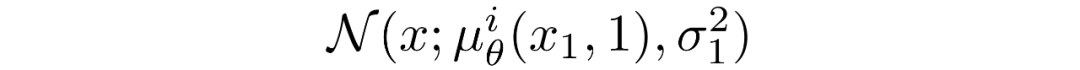
其中t=1 的像素分布源自下面的多元高斯分布,其對角協方差矩陣允許我們將分布拆分為單變量高斯分布的乘積,每個高斯分布對應數據的每個維度:
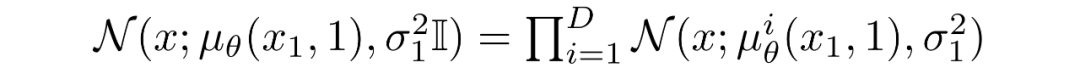
我們假設圖像由 0,1,...,255(作為標準 RGB 圖像)中的整數組成,這些整數已線性縮放到 [?1,1]。其中,對于給定的像素值 x,該像素值的連續變化范圍是 [x?1/255,x+1/255]。給定中相應像素的單變量高斯分布,像素值 x 的概率是以 x為中心的 [x?1/255,x+1/255]范圍內的單變量高斯分布下的面積區域。
下面你可以看到每個范圍中的面積及其均值為 0 高斯的概率,在這種情況下,對應于平均像素值為 255/2(半亮度)的分布。
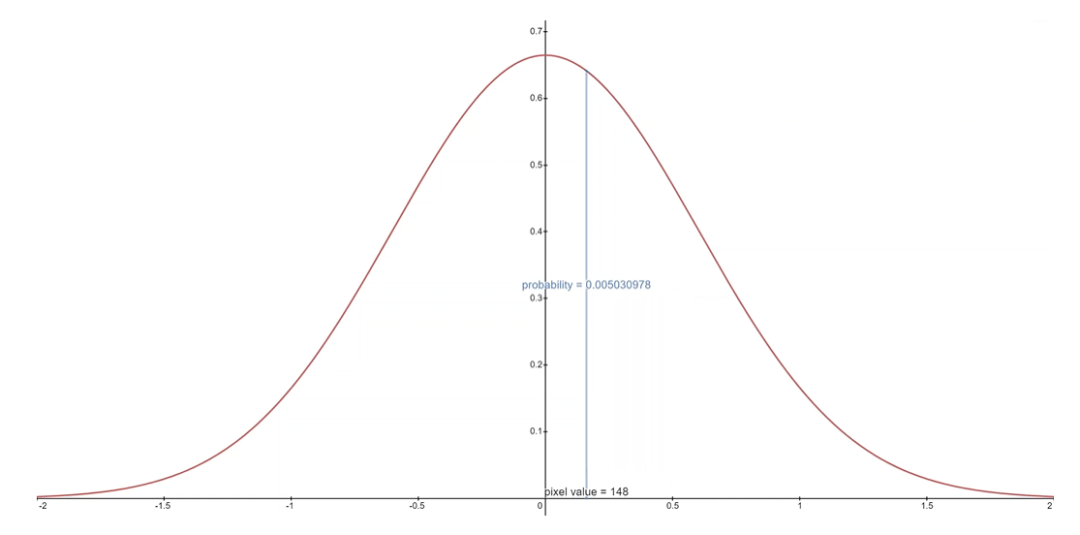
對于每個像素,給定t=0時刻的像素值,就是簡單的相乘就可以,這個過程可以用下面的式子表示:
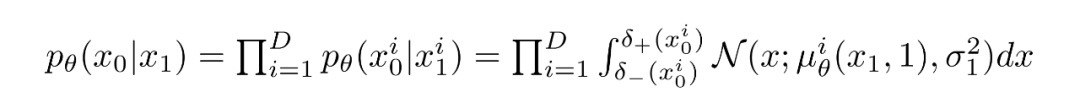
其中
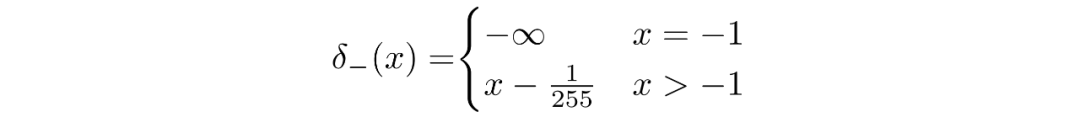
并且
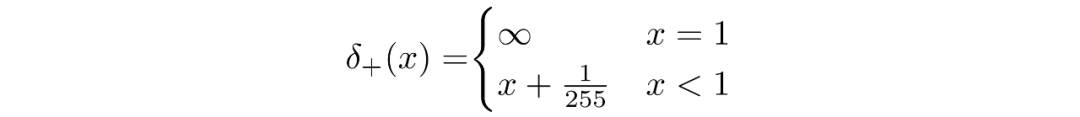
給定了的等式,我們可以計算出最終的的形式,并不是和KL散度一樣的形式:
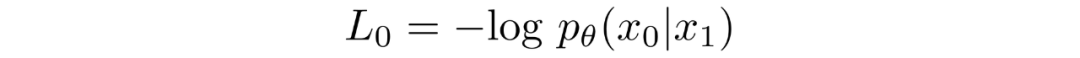
最終目標
如上一節所述,作者發現預測給定時間步長的圖像產生了最好的結果。最終,他們使用以下目標:
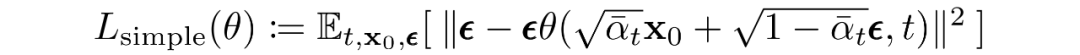
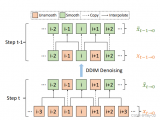
我們的擴散模型的訓練和采樣算法可見下圖:

擴散模型總結
在本節中,我們詳細探討了擴散模型的理論。人們很容易陷入數學細節,因此我們在下面記錄了最重要的要點,以便讓我們從總體的角度來定位:
我們的擴散模型被參數化為馬爾可夫鏈,這意味著我們的潛變量僅取決于之前(或之后)的時間步長。
馬爾可夫鏈中的變換分布是高斯的,正向過程需要方差策略,逆向過程的參數是學習的。
擴散過程確保對于足夠大的 T,漸近分布為各向同性高斯分布。
在我們的案例中,方差策略是固定的,但它也可以學習。對于固定策略,遵循幾何級數可能比線性級數提供更好的結果。在任一情況下,序列中的方差通常隨時間增加。
擴散模型高度靈活,允許使用輸入和輸出維度相同的任何架構。許多實現使用 U-Net-like架構。
訓練目標是最大化訓練數據的似然。這表現為調整模型參數以最小化數據負對數似然的變分上限。
由于我們的馬爾可夫假設,目標函數中的幾乎所有項都可以轉換為 KL 散度。鑒于我們使用的是高斯分布,這些值變得可以計算,因此無需執行蒙特卡羅近似。
最終,使用簡化的訓練目標來訓練預測給定潛變量的噪聲分量的函數會產生最佳和最穩定的結果。
作為反向擴散過程的最后一步,離散解碼器用于獲取像素值的對數似然。
有了這個擴散模型的高級概述,讓我們繼續看看如何在 PyTorch 中使用擴散模型。
PyTorch中的擴散模型
雖然擴散模型還沒有像機器學習中其他結構/方法那樣有很多人的實現,但仍有可用的實現。在 PyTorch 中使用擴散模型的最簡單方法是使用denoising-diffusion-pytorch包,它實現了本文中討論的圖像擴散模型。要安裝軟件包,只需在終端中鍵入以下命令:
pip?install?denoising_diffusion_pytorch
Minimal Example
為了訓練模型生成圖像,我們首先導入必要的包:
import?torch from?denoising_diffusion_pytorch?import?Unet,?GaussianDiffusion
然后,我們定義網絡結構,這里用U-Net,參數中的dim表示第一次下采樣之前的特征圖的數量,dim_mults參數提了每次下采樣時,通道數的乘數。
model?=?Unet( ????dim?=?64, ????dim_mults?=?(1,?2,?4,?8) )? 現在,網絡結構定義好了,我們需要定義擴散模型本身,我們將U-Net模型作為參數輸入到擴散模型中,還有其他幾個參數,生成的圖像的尺寸,擴散過程的步數,選擇L1還是L2歸一化。 ?
diffusion?=?GaussianDiffusion( ????model, ????image_size?=?128, ????timesteps?=?1000,???#?number?of?steps ????loss_type?=?'l1'????#?L1?or?L2 )
現在,擴散模型定義好了,我們通過生成隨機數據來訓練,然后使用常用的流程來訓練:
training_images?=?torch.randn(8,?3,?128,?128) loss?=?diffusion(training_images) loss.backward()
模型訓練完成后,我們最終可以使用 diffusion 對象的 sample() 方法生成圖像。這里我們生成 4 張圖像,由于我們的訓練數據是隨機的,我們也只能得到噪聲:
sampled_images?=?diffusion.sample(batch_size?=?4)
在自定義數據集上訓練
denoising-diffusion-pytorch 包還允許你在特定數據集上訓練擴散模型。只需將下面的 Trainer() 對象中的 path/to/your/images 字符串替換為數據集目錄路徑,并將 image_size更改為適當的值。之后,只需運行代碼來訓練模型,然后像以前一樣進行采樣。請注意,PyTorch 必須在啟用 CUDA 的情況下編譯才能使用 Trainer 類:
from?denoising_diffusion_pytorch?import?Unet,?GaussianDiffusion,?Trainer model?=?Unet( ????dim?=?64, ????dim_mults?=?(1,?2,?4,?8) ).cuda() diffusion?=?GaussianDiffusion( ????model, ????image_size?=?128, ????timesteps?=?1000,???#?number?of?steps ????loss_type?=?'l1'????#?L1?or?L2 ).cuda() trainer?=?Trainer( ????diffusion, ????'path/to/your/images', ????train_batch_size?=?32, ????train_lr?=?2e-5, ????train_num_steps?=?700000,?????????#?total?training?steps ????gradient_accumulate_every?=?2,????#?gradient?accumulation?steps ????ema_decay?=?0.995,????????????????#?exponential?moving?average?decay ????amp?=?True????????????????????????#?turn?on?mixed?precision ) trainer.train()
下面你可以看到從多元高斯噪聲到MNIST數字的漸進去噪,類似于反向擴散:

審核編輯:黃飛
 電子發燒友App
電子發燒友App






























評論