編輯:祝鑫泉
概述
梯度下降算法(Gradient Descent Optimization)是神經(jīng)網(wǎng)絡(luò)模型訓(xùn)練最常用的優(yōu)化算法。對于深度學(xué)習(xí)模型,基本都是采用梯度下降算法來進(jìn)行優(yōu)化訓(xùn)練的。梯度下降算法背后的原理:目標(biāo)函數(shù)
關(guān)于參數(shù)的梯度將是目標(biāo)函數(shù)上升最快的方向。對于最小化優(yōu)化問題,只需要將參數(shù)沿著梯度相反的方向前進(jìn)一個步長,就可以實(shí)現(xiàn)目標(biāo)函數(shù)的下降。這個步長又稱為學(xué)習(xí)速率。參數(shù)更新公式如下:
其中
是參數(shù)的梯度,根據(jù)計(jì)算目標(biāo)函數(shù)采用數(shù)據(jù)量的不同,梯度下降算法又可以分為批量梯度下降算法(Batch Gradient Descent),隨機(jī)梯度下降算法(Stochastic GradientDescent)和小批量梯度下降算法(Mini-batch Gradient Descent)。對于批量梯度下降算法,其是在整個訓(xùn)練集上計(jì)算的,如果數(shù)據(jù)集比較大,可能會面臨內(nèi)存不足問題,而且其收斂速度一般比較慢。隨機(jī)梯度下降算法是另外一個極端,是針對訓(xùn)練集中的一個訓(xùn)練樣本計(jì)算的,又稱為在線學(xué)習(xí),即得到了一個樣本,就可以執(zhí)行一次參數(shù)更新。所以其收斂速度會快一些,但是有可能出現(xiàn)目標(biāo)函數(shù)值震蕩現(xiàn)象,因?yàn)楦哳l率的參數(shù)更新導(dǎo)致了高方差。小批量梯度下降算法是折中方案,選取訓(xùn)練集中一個小批量樣本計(jì)算,這樣可以保證訓(xùn)練過程更穩(wěn)定,而且采用批量訓(xùn)練方法也可以利用矩陣計(jì)算的優(yōu)勢。這是目前最常用的梯度下降算法。
對于神經(jīng)網(wǎng)絡(luò)模型,借助于BP算法可以高效地計(jì)算梯度,從而實(shí)施梯度下降算法。但梯度下降算法一個老大難的問題是:不能保證全局收斂。如果這個問題解決了,深度學(xué)習(xí)的世界會和諧很多。梯度下降算法針對凸優(yōu)化問題原則上是可以收斂到全局最優(yōu)的,因?yàn)榇藭r(shí)只有唯一的局部最優(yōu)點(diǎn)。而實(shí)際上深度學(xué)習(xí)模型是一個復(fù)雜的非線性結(jié)構(gòu),一般屬于非凸問題,這意味著存在很多局部最優(yōu)點(diǎn)(鞍點(diǎn)),采用梯度下降算法可能會陷入局部最優(yōu),這應(yīng)該是最頭疼的問題。這點(diǎn)和進(jìn)化算法如遺傳算法很類似,都無法保證收斂到全局最優(yōu)。因此,我們注定在這個問題上成為“高級調(diào)參師”。可以看到,梯度下降算法中一個重要的參數(shù)是學(xué)習(xí)速率,適當(dāng)?shù)膶W(xué)習(xí)速率很重要:學(xué)習(xí)速率過小時(shí)收斂速度慢,而過大時(shí)導(dǎo)致訓(xùn)練震蕩,而且可能會發(fā)散。理想的梯度下降算法要滿足兩點(diǎn):收斂速度要快;能全局收斂。為了這個理想,出現(xiàn)了很多經(jīng)典梯度下降算法的變種,下面將分別介紹它們。
01
Momentum optimization
沖量梯度下降算法是BorisPolyak在1964年提出的,其基于這樣一個物理事實(shí):將一個小球從山頂滾下,其初始速率很慢,但在加速度作用下速率很快增加,并最終由于阻力的存在達(dá)到一個穩(wěn)定速率。對于沖量梯度下降算法,其更新方程如下:
可以看到,參數(shù)更新時(shí)不僅考慮當(dāng)前梯度值,而且加上了一個積累項(xiàng)(沖量),但多了一個超參
02
NAG
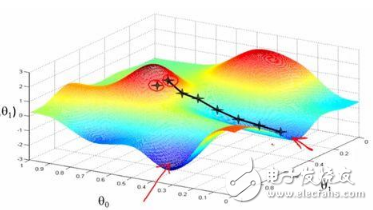
NAG算法全稱Nesterov Accelerated Gradient,是YuriiNesterov在1983年提出的對沖量梯度下降算法的改進(jìn)版本,其速度更快。其變化之處在于計(jì)算“超前梯度”更新沖量項(xiàng),具體公式如下:
既然參數(shù)要沿著
圖1 NAG效果圖
03
AdaGrad
AdaGrad是Duchi在2011年提出的一種學(xué)習(xí)速率自適應(yīng)的梯度下降算法。在訓(xùn)練迭代過程,其學(xué)習(xí)速率是逐漸衰減的,經(jīng)常更新的參數(shù)其學(xué)習(xí)速率衰減更快,這是一種自適應(yīng)算法。其更新過程如下:
其中是梯度平方的積累量,在進(jìn)行參數(shù)更新時(shí),學(xué)習(xí)速率要除以這個積累量的平方根,其中加上一個很小值是為了防止除0的出現(xiàn)。由于是該項(xiàng)逐漸增加的,那么學(xué)習(xí)速率是衰減的。考慮如圖2所示的情況,目標(biāo)函數(shù)在兩個方向的坡度不一樣,如果是原始的梯度下降算法,在接近坡底時(shí)收斂速度比較慢。而當(dāng)采用AdaGrad,這種情況可以被改觀。由于比較陡的方向梯度比較大,其學(xué)習(xí)速率將衰減得更快,這有利于參數(shù)沿著更接近坡底的方向移動,從而加速收斂。
圖2 AdaGrad效果圖
前面說到AdaGrad其學(xué)習(xí)速率實(shí)際上是不斷衰減的,這會導(dǎo)致一個很大的問題,就是訓(xùn)練后期學(xué)習(xí)速率很小,導(dǎo)致訓(xùn)練過早停止,因此在實(shí)際中AdaGrad一般不會被采用,下面的算法將改進(jìn)這一致命缺陷。不過TensorFlow也提供了這一優(yōu)化器:tf.train.AdagradOptimizer。
04
RMSprop
RMSprop是Hinton在他的課程上講到的,其算是對Adagrad算法的改進(jìn),主要是解決學(xué)習(xí)速率過快衰減的問題。其實(shí)思路很簡單,類似Momentum思想,引入一個超參數(shù),在積累梯度平方項(xiàng)進(jìn)行衰減:
可以認(rèn)為僅僅對距離時(shí)間較近的梯度進(jìn)行積累,其中一般取值0.9,其實(shí)這樣就是一個指數(shù)衰減的均值項(xiàng),減少了出現(xiàn)的爆炸情況,因此有助于避免學(xué)習(xí)速率很快下降的問題。同時(shí)Hinton也建議學(xué)習(xí)速率設(shè)置為0.001。RMSprop是屬于一種比較好的優(yōu)化算法了,在TensorFlow中當(dāng)然有其身影:tf.train.RMSPropOptimizer(learning_rate=learning_rate,momentum=0.9, decay=0.9, epsilon=1e-10)。
不得不說點(diǎn)題外話,同時(shí)期還有一個Adadelta算法,其也是Adagrad算法的改進(jìn),而且改進(jìn)思路和RMSprop很像,但是其背后是基于一次梯度近似代替二次梯度的思想,感興趣的可以看看相應(yīng)的論文,這里不再贅述。
05
AdamAdam全稱Adaptive moment estimation,是Kingma等在2015年提出的一種新的優(yōu)化算法,其結(jié)合了Momentum和RMSprop算法的思想。相比Momentum算法,其學(xué)習(xí)速率是自適應(yīng)的,而相比RMSprop,其增加了沖量項(xiàng)。所以,Adam是兩者的結(jié)合體:
可以看到前兩項(xiàng)和Momentum和RMSprop是非常一致的,由于和的初始值一般設(shè)置為0,在訓(xùn)練初期其可能較小,第三和第四項(xiàng)主要是為了放大它們。最后一項(xiàng)是參數(shù)更新。其中超參數(shù)的建議值是
學(xué)習(xí)速率
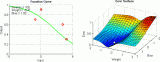
前面也說過學(xué)習(xí)速率的問題,對于梯度下降算法,這應(yīng)該是一個最重要的超參數(shù)。如果學(xué)習(xí)速率設(shè)置得非常大,那么訓(xùn)練可能不會收斂,就直接發(fā)散了;如果設(shè)置的比較小,雖然可以收斂,但是訓(xùn)練時(shí)間可能無法接受;如果設(shè)置的稍微高一些,訓(xùn)練速度會很快,但是當(dāng)接近最優(yōu)點(diǎn)會發(fā)生震蕩,甚至無法穩(wěn)定。不同學(xué)習(xí)速率的選擇影響可能非常大,如圖3所示。
圖3 不同學(xué)習(xí)速率的訓(xùn)練效果
理想的學(xué)習(xí)速率是:剛開始設(shè)置較大,有很快的收斂速度,然后慢慢衰減,保證穩(wěn)定到達(dá)最優(yōu)點(diǎn)。所以,前面的很多算法都是學(xué)習(xí)速率自適應(yīng)的。除此之外,還可以手動實(shí)現(xiàn)這樣一個自適應(yīng)過程,如實(shí)現(xiàn)學(xué)習(xí)速率指數(shù)式衰減:
在TensorFlow中,你可以這樣實(shí)現(xiàn):
initial_learning_rate = 0.1
decay_steps = 10000
decay_rate = 1/10
global_step = tf.Variable(0, trainable=False)
learning_rate = tf.train.exponential_decay(initial_learning_rate,
global_step, decay_steps, decay_rate)
# decayed_learning_rate = learning_rate *
# decay_rate ^ (global_step / decay_steps)
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)
training_op = optimizer.minimize(loss, global_step=global_step)
總結(jié)
本文簡單介紹了梯度下降算法的分類以及常用的改進(jìn)算法,總結(jié)來看,優(yōu)先選擇學(xué)習(xí)速率自適應(yīng)的算法如RMSprop和Adam算法,大部分情況下其效果是較好的。還有一定要特別注意學(xué)習(xí)速率的問題。其實(shí)還有很多方面會影響梯度下降算法,如梯度的消失與爆炸,這也是要額外注意的。最后不得不說,梯度下降算法目前無法保證全局收斂還將是一個持續(xù)性的數(shù)學(xué)難題。
參考文獻(xiàn)
Anoverview of gradient descent optimization algorithms: .
Hands-OnMachine Learning with Scikit-Learn and TensorFlow, Aurélien Géron, 2017.
NAG:.
Adagrad:.
RMSprop:~tijmen/csc321/slides/lecture_slides_lec6.pdf.
Adadelta:https://arxiv.org/pdf/1212.5701v1.pdf.
Adam:https://arxiv.org/pdf/1412.6980.pdf.
不同的算法的效果可視化:https://imgur.com/a/Hqolp.
歡迎大家加群在群中探討
歡迎留言或贊賞。
推
薦
閱
讀
Object Detection R-CNN
掃描個人微信號,
拉你進(jìn)機(jī)器學(xué)習(xí)大牛群。
福利滿滿,名額已不多…
80%的AI從業(yè)者已關(guān)注我們微信公眾號
 電子發(fā)燒友App
電子發(fā)燒友App











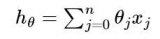
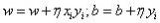
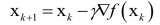










評論