什么是自適應濾波器

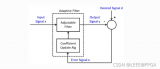
　　自適應濾波器是能夠根據輸入信號自動調整性能進行數字信號處理的數字濾波器。作為對比，非自適應濾波器有靜態的濾波器系數，這些靜態系數一起組成傳遞函數。

　　對于一些應用來說，由于事先并不知道所需要進行操作的參數，例如一些噪聲信號的特性，所以要求使用自適應的系數進行處理。在這種情況下，通常使用自適應濾波器，自適應濾波器使用反饋來調整濾波器系數以及頻率響應。

　　總的來說，自適應的過程涉及到將代價函數用于確定如何更改濾波器系數從而減小下一次迭代過程成本的算法。價值函數是濾波器最佳性能的判斷準則，比如減小輸入信號中的噪聲成分的能力。

　　隨著數字信號處理器性能的增強，自適應濾波器的應用越來越常見，時至今日它們已經廣泛地用于手機以及其它通信設備、數碼錄像機和數碼照相機以及醫療監測設備中。

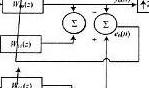
　　下面圖示的框圖是最小均方濾波器（LMS）和遞歸最小平方（en:Recursive least squares filter，RLS，即我們平時說的最小二乘法）這些特殊自適應濾波器實現的基礎。框圖的理論基礎是可變濾波器能夠得到所要信號的估計。

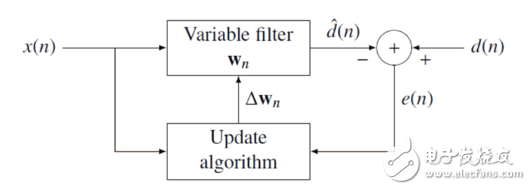
　　自適應濾波器有4種基本應用類型：

　　1） 系統辨識：這時參考信號就是未知系統的輸出，當誤差最小時，此時自適應濾波器就與未知系統具有相近的特性，自適應濾波器用來提供一個在某種意義上能夠最好擬合未知裝置的線性模型

　　2） 逆模型：在這類應用中，自適應濾波器的作用是提供一個逆模型，該模型可在某種意義上最好擬合未知噪聲裝置。理想地，在線性系統的情況下，該逆模型具有等于未知裝置轉移函數倒數的轉移函數，使得二者的組合構成一個理想的傳輸媒介。該系統輸入的延遲構成自適應濾波器的期望響應。在某些應用中，該系統輸入不加延遲地用做期望響應。

　　3） 預測：在這類應用中，自適應濾波器的作用是對隨機信號的當前值提供某種意義上的一個最好預測。于是，信號的當前值用作自適應濾波器的期望響應。信號的過去值加到濾波器的輸入端。取決于感興趣的應用，自適應濾波器的輸出或估計誤差均可作為系統的輸出。在第一種情況下，系統作為一個預測器；而在后一種情況下，系統作為預測誤差濾波器。

　　4） 干擾消除：在一類應用中，自適應濾波器以某種意義上的最優化方式消除包含在基本信號中的未知干擾。基本信號用作自適應濾波器的期望響應，參考信號用作濾波器的輸入。參考信號來自定位的某一傳感器或一組傳感器，并以承載新息的信號是微弱的或基本不可預測的方式，供給基本信號上。

　　這也就是說，得到期望輸出往往不是引入自適應濾波器的目的，引入它的目的是得到未知系統模型、得到未知信道的傳遞函數的倒數、得到未來信號或誤差和得到消除干擾的原信號。

　　自適應濾波通俗點講就是混合信號向期望信號的逼近。在逼近的過程中，根據觀測信號與真實（期望）信號的均放誤差（MSE）為量化指標，按照一定規則進行迭代（迭代規則自己可以設定），直到算法收斂（收斂條件有很多，比如達到預先設定的迭代次數、或達到允許的誤差等）。現有的常見自適應算法有RLS，LMS，NLMS，往往都是按照梯度下降法或牛頓法進行迭代。

　　算法背景

　　經典的濾波算法包括維納濾波，卡爾曼濾波，這些濾波算法都需要對輸入信號的相關系數，噪聲功率等參數進行估計，而實際中很難實現這些參數的準確估計，而這些參數的準確估計直接影響到濾波器的濾波效果。另一方面，這兩類濾波器一般設計完成，參數便不可改變，實際應用中，希望濾波器的參數能夠隨著輸入信號的變化而改變，以取得較好的實時性處理效果。為了彌補傳統濾波算法的不足，滿足信號處理的要求，又發展了自適應濾波。

　　算法基本原理

　　自適應濾波與維納濾波，卡爾曼濾波最大的區別在于，自適應濾波在輸出與濾波系統之間存在有反饋通道，根據某一時刻濾波器的輸出與期望信號的誤差調整濾波器的系數，從而實現濾波器系數的動態調整，實現最優濾波。

　　（1）信號模型

　　自適應濾波的目的仍然是從觀測信號中提取真實準確的期望信號，因此涉及到的信號有：

　　期望信號 d（n）

　　輸入信號 x（n）=d（n）+v（n）

　　輸出信號 y（n）

　　（2）算法原理

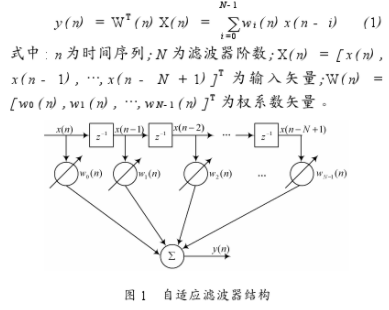
　　一個M階濾波器，系數為w（m），則輸出為：

　　y（n）=Σw（m）x（n-m） m=0…M

　　寫成矩陣形式： y（j）=WT（j）*X（j）

　　n時刻的輸出誤差為： e（j）=d（j）-y（j）= d（j）- WT（j）*X（j）

　　定義目標函數為 E［e（j）^2］，則有：

　　J（j）=E［e（j）^2］= E［（d（j）- WT（j）*X（j））^2］

　　當上述誤差達到最小時，即實現最優濾波，這種目標函數確定的為最小方差自適應濾波。

　　對于目標函數J（j），需要求得使其取到最小值對應的W，這里使用梯度下降法進行最優化：

　　W（j+1）=W（j）+1/2*μ（-▽J（j））

　　▽J（j）=-2E［X（j）*（ d（j）- WT（j）*X（j））］= -2E［X（j）e（j）］

　　W（j+1）=W（j）+μE［X（j）e（j）］

　　其中-2X（j）e（j）稱為瞬時梯度，因為瞬時梯度是真實梯度的無偏估計，這里可以使用瞬時梯度代替真實梯度。

　　W（j+1）=W（j）+μX（j）e（j）

　　由此，可以得到自適應濾波最佳系數的迭代公式。

　　3.算法的收斂性

　　在最小均方誤差自適應濾波算法中，最佳濾波器系數應該滿足：

　　▽J（j）=0

　　即：-2E［X（j）*（ d（j）- WT（j）*X（j））］=0

　　經整理后，可以得到：

　　WoptT =Rxx-1*Rxd

　　上式說明，自適應濾波的最佳濾波器系數同維納濾波相同，與輸入信號以及期望信號的相關矩陣有關。

　　對W（j+1）=W（j）+μX（j）e（j）等號兩邊求期望，并通過一系列推導，可得：

　　E［W（j+1）］=Wopt+Q（I-μΛ）jQH（W0-Wopt）

　　式中Rxx=QHΛQ， W0為自適應濾波系數的初值。

　　當j取到無窮大時，濾波器應達到最優狀態，因此：

　　（I-μΛ）j=0，則有：|I-μΛ|《=1

　　上式即為最小均方自適應濾波的收斂條件。

　　Λ為輸入信號的自相關矩陣Rxx的特征值構成的對角陣。

　　4.變步長自適應濾波算法

　　在整個迭代過程中，步長不變的情況稱為定步長算法。為了保證算法的收斂性，一般要取一個比較小的步長值，但步長過小又容易導致算法收斂過慢。比較理想的情況是，在迭代的初始階段，誤差值較大時，取一個較大的迭代步長，以實現較快的收斂速度；隨著迭代次數增加，誤差逐漸減小，步長也應相應減小，達到較高的收斂精度。這種思想便稱為變步長自適應濾波算法。

　　常用的變步長自適應濾波算法根據輸入信號的或者誤差值確定步長。

　　這里介紹兩種具體的變步長算法：

　　（1）歸一化變步長自適應濾波算法

　　μj =α/（β+XjTXj）

　　α，β均為常數，且滿足0《α《2，β》=0。

　　該算法使用輸入信號的能量對步長因子進行歸一化，確保其取到合適的值。

　　（2）Sigmod函數變步長自適應濾波算法

　　μj=β（1-exp（-αej^2））

　　α，β均為常數，且滿足0《α，0=《β《μmax。

　　從上述表達式中可以明顯看出，隨著誤差增大，步長值也增大。

　　5.解相關自適應濾波算法

　　實驗發現，當輸入信號之間的相關性比較強時，自適應濾波的效果比較差。因此需要去除相鄰兩次輸入信號序列的相關性，以得到較好的濾波效果。

　　解相關自適應濾波算法的實現過程為：

　　r= XjTXj-1/ Xj-1TXj-1

　　Zj=Xj-rXj-1

　　μj=βej/ ZjTXj

　　Wj+1=Wj+μjZj

　　6.變換域自適應濾波算法

　　根據解相關自適應濾波算法的思想，使用一組正交基對輸入信號進行變換，在變換域上進行自適應濾波，最后再將濾波結果逆變換至時間域。常見的變換有傅里葉變換，分數階傅里葉變換，小波變換，余弦變換。

　　算法應用與實現

　　下面講述如何在實際問題中應用自適應濾波算法：

　　問題背景：一個點目標在x，y平面上繞單位圓做圓周運動，由于外界干擾，其運動軌跡發生了偏移。其中，x方向的干擾為均值為0，方差為0.05的高斯噪聲；y方向干擾為均值為0，方差為0.06的高斯噪聲。

　　問題分析與思路：

　　將物體的運動軌跡分解為X方向和Y方向，并假設兩個方向上運動相互獨立。分別將運動軌跡離散為一系列點，作為濾波器的輸入，分別在兩個方向上進行濾波，最終再合成運動軌跡。

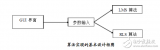
　　程序設計思路：

　　生成期望信號-添加噪聲-設置濾波器系數初值-迭代運算-最優濾波輸出

　　濾波結果分析：

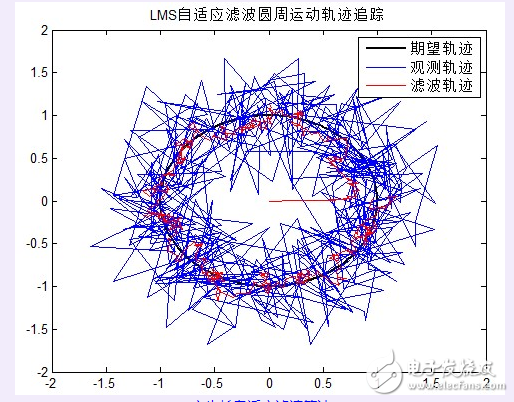
?定步長自適應濾波算法

　　變步長自適應濾波算法

　　解相關自適應濾波算法