前言
本文簡述了機器學習核心結構的歷史發展,并總結了研究者需要熟知的 8 個神經網絡架構。
我們為什么需要「機器學習」?
機器學習對于那些我們直接編程太過復雜的任務來說是必需的。有些任務很復雜,以至于人類不可能解決任務中所有的細節并精確地編程。所以,我們向機器學習算法提供大量的數據,讓算法通過探索數據并找到一個可以實現程序員目的的模型來解決這個問題。
我們來看兩個例子:
寫一個程序去識別復雜場景中照明條件下新視角的三維物體是很困難的。我們不知道編寫什么程序,因為我們并不了解它在我們大腦中運作的機制,即便知道如何實現,寫出來的程序也可能會非常復雜。
寫一個程序去計算信用卡詐騙的概率是很困難的。因為可能沒有任何既簡單又可靠的規則,我們需要結合大量的弱規則去判別。欺騙是可以轉移目標的,程序需要不斷更改。
接著出現了機器學習方法:我們不需為每個特定的任務手動編程,只要收集大量的樣本,為給定的輸入指定正確的輸出。機器學習算法利用這些樣本去生成完成指定工作的程序。學習算法產生的程序可能與典型的手寫程序非常不同,它可能包含數百萬個數字。如果我們做得正確,這個程序將像處理訓練集上的樣本一樣來處理新樣本。如果數據改變,程序也可以通過訓練新數據改變。你應該注意到,目前大量的計算比支付給程序員編寫一個特定任務的程序便宜。
鑒于此,機器學習最適用任務的例子包括:
模式識別:真實場景中的物體,面部識別或面部表情,口語。
異常識別:不尋常的信用卡交易序列,核電站傳感器讀數的異常模式。
預測:未來股票價格或貨幣匯率,一個人喜歡什么電影。
什么是神經網絡?
神經網絡是機器學習文獻中的一類模型。例如,如果你參加了 Coursera 的機器學習課程,很可能會學到神經網絡。神經網絡是一套特定的算法,它徹底改變了機器學習領域。他們受到生物神經網絡的啟發,目前深度神經網絡已經被證實效果很好。神經網絡本身是一般的函數逼近,這就是為什么它們幾乎可以應用于任何從輸入到輸出空間復雜映射的機器學習問題。
以下是說服你學習神經計算的三個理由:
了解大腦是如何工作的:它非常大且很復雜,一旦破壞就會腦死亡,所以我們需要使用計算機模擬。
了解受神經元及其適應性連接啟發的并行計算風格:這種風格與序列計算截然不同。
使用受大腦啟發的新穎學習算法來解決實際問題:即使不是大腦的實際工作方式,學習算法也非常有用。
在完成吳恩達的 Coursera 機器學習課程后,我開始對神經網絡和深度學習產生興趣,因此尋找最好的網上資源來了解這個主題,并找到了 Geoffrey Hinton 的機器學習神經網絡課程。如果你正在做深度學習的工程或想要踏入深度學習/機器學習的領域,你應該參加這個課程。Geoffrey Hinton 毫無疑問是深度學習領域的教父,在課程中給出了非凡的見解。在這篇博客文章中,我想分享我認為任何機器學習研究人員都應該熟悉的八個神經網絡架構,以促進他們的工作。
一般來說,這些架構可分為三類:
1. 前饋神經網絡
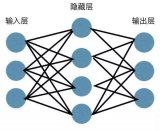
這是實際應用中最常見的神經網絡類型。第一層是輸入,最后一層是輸出。如果有多個隱藏層,我們稱之為「深度」神經網絡。他們計算出一系列改變樣本相似性的變換。各層神經元的活動是前一層活動的非線性函數。
2. 循環網絡
循環網絡在他們的連接圖中定向了循環,這意味著你可以按照箭頭回到你開始的地方。他們可以有復雜的動態,使其很難訓練。他們更具有生物真實性。
目前如何高效地訓練循環網絡正在受到廣泛關注。循環神經網絡是模擬連續數據的一種非常自然的方式。它們相當于每個時間片段具有一個隱藏層的深度網絡;除此之外,它們在每個時間片段上使用相同的權重并且在每個時間片段上輸入。它們可以長時間記住隱藏狀態的信息,但很難訓練其使用這個潛能。
3. 對稱連接網絡
對稱連接網絡有點像循環網絡,但是單元之間的連接是對稱的(它們在兩個方向上權重相同)。比起循環網絡,對稱連接網絡更容易分析。這個網絡中有更多的限制,因為它們遵守能量函數定律。沒有隱藏單元的對稱連接網絡被稱為「Hopfield 網絡」。有隱藏單元的對稱連接的網絡被稱為玻爾茲曼機。
下面介紹研究者需要熟知的 8 個神經網絡架構。
1. 感知器
第一代神經網絡出現時,感知機(perceptron)僅僅是單個神經元的計算模型,其在二十世紀六十年代初被美國計算機科學家 Frank Rosenblatt 推廣。其學習算法非常強大,并且宣稱可以學習很多事情。1969 年,Minsky 與 Papert 出版了一本名為《感知機》的書,這本書分析了這些算法可以做什么,并闡釋了其局限性。許多人就將這個局限性放大到所有的 NN 模型。然而,感知機學習過程仍廣泛用于具有包含數百萬特征的大特征向量的任務。
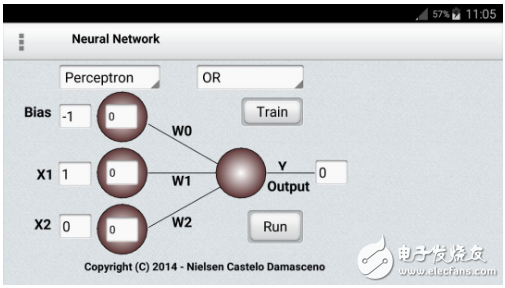
在統計模式識別的標準范例中,我們首先將原始輸入向量轉換為特征激活向量。然后,基于大家的共識手動編程來定義特征。接下來,我們學習如何對每個特征激活進行加權以獲得單一的標量。如果這個標量超過了某個閾值,我們認為輸入向量是目標集中的一個正樣本。
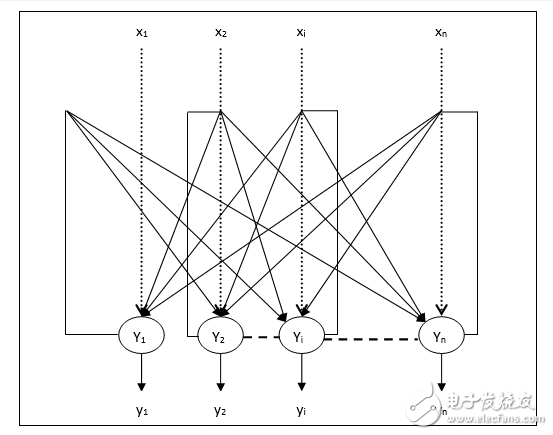
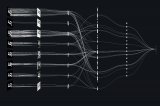
標準的感知機架構遵循前饋模型,輸入被發送到神經元中,經處理后輸出。在下圖中,表示為網絡自下而上讀取:底部輸入,頂部輸出。
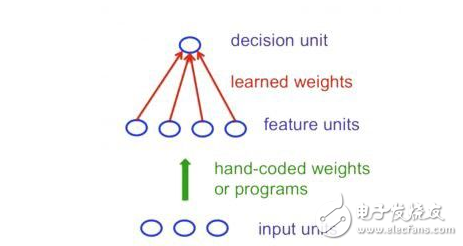
但是,感知機確實存在局限性:如果您使用手動設置特征,并且使用了足夠多的特征,那么你幾乎可以做任何事情。對于二進制輸入向量,我們可以為指數級多的二進制向量分別設置一個特征單元,因此我們可以對二進制輸入向量進行任何可能的區分。但是,一旦確定了手動編程的特征,感知器可以學習的東西就非常有限。
這個結果對于感知機是毀滅性的,因為模式識別是去識別在變換情況下的模式。Minsky 和 Papert 的「組不變性定理」認為感知機的學習部分無法去學習當轉換來自于一個組的情況。為了識別上述那種情況,需要更多的特征單元去識別那些模式中包含的子信息。所以模式識別的技巧部分必須由手動編碼的特征檢測器來解決,而不是學習過程。
沒有隱藏單元的網絡在其可以學習建模的輸入輸出映射中是非常有限的。簡單地增加一些線性單元無濟于事,因為結果還是線性的。固定的輸出非線性也不夠,因此,我們需要多層自適應非線性隱藏單元。問題是怎樣對這樣的網絡進行訓練。我們需要一種適應所有權重的有效方式,而不僅僅是最后一層,所以這很難。學習進入隱藏層的權重等同于學習特征,這是非常困難的,因為沒有人直接告訴我們隱藏層應該怎么做。
2. 卷積神經網絡
機器學習研究已經廣泛地集中在物體檢測問題上。有各種各樣的事情使識別物體變得困難:
圖像分割:真實場景中總是摻雜著其它物體。很難判斷哪些部分屬于同一個對象。對象的某些部分可以隱藏在其他對象的后面。
物體光照:像素的強度被光照強烈影響。
圖像變形:物體可以以各種非仿射方式變形。例如,手寫也可以有一個大的圓圈或只是一個尖頭。
情景支持:物體所屬類別通常由它們的使用方式來定義。例如,椅子是為了讓人們坐在上面而設計的,因此它們具有各種各樣的物理形狀。
視角:標準學習方法無法應對的視點變化導致的圖像變化,得到的信息隨輸入維度(即像素)的變化而變化。
維度跳變:設想一個醫療數據庫,通常用來學習體重的神經元,現在忽然用來學習病人的年齡!要應用機器學習,我們首先要消除這個維度跳躍。
復制特征方法是目前神經網絡解決目標檢測問題的主要方法。在不同的位置使用相同的特征提取器。它也可以在尺寸和方向上復制,這很需技巧并且很貴。復制大大減少了要學習的自由參數的數量。它使用幾種不同的特征類型,每種都有自己的復制檢測器圖像。它也允許以各種方式表示每個圖像塊。
那么復制特征檢測器是如何實現的呢?
激活值等變化量:復制特征的方法并不能使神經元激活值不變,但是能夠使激活值改變量相同。
知識不變量:如果在訓練中一個特征在某些位置有效,則在測試過程中,特征檢測器在各個位置有效。
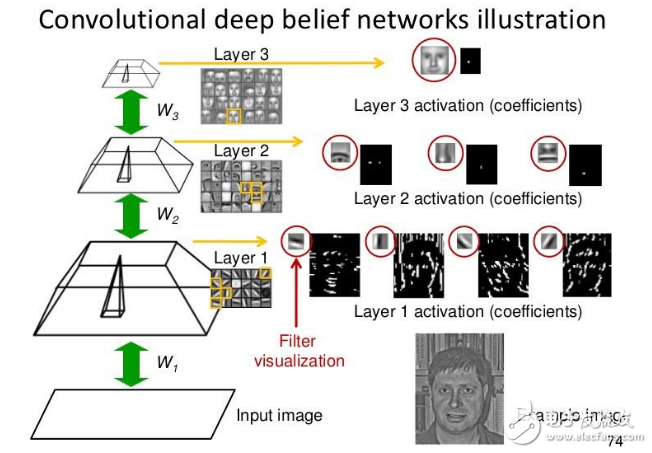
1998 年,Yann LeCun 和他的合作者開發了 LeNet 的手寫數字識別器。它在前饋網中使用反向傳播,這個前饋網絡不僅僅是一個識別器,它有許多隱藏層,每個層有許多復制單元的映射,匯集附近復制單元的輸出,有一個即使重疊也能夠同時處理幾個字符的寬網,以及訓練一套完整的系統的巧妙方式。后來正式命名為卷積神經網絡。一個有趣的事實是:這個網絡被用來讀取北美地區約 10%的支票。
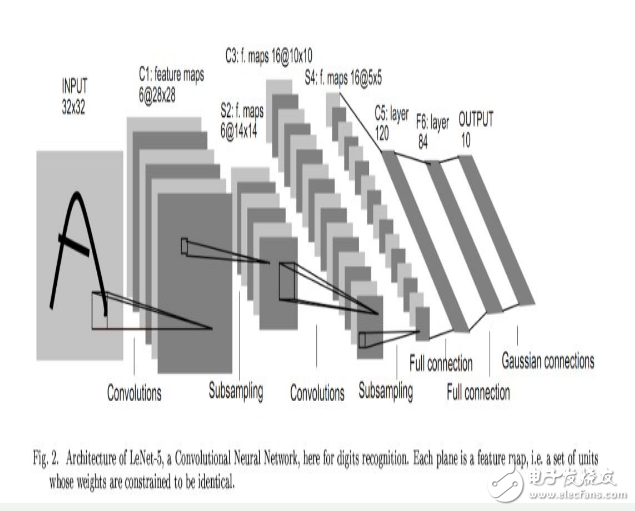
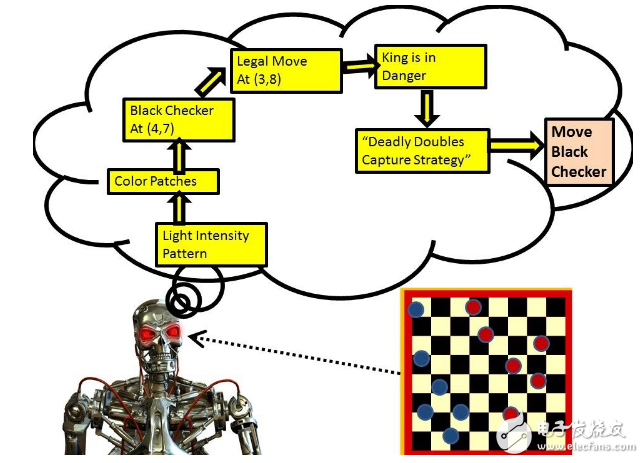
卷積神經網絡可用于從手寫數字到 3D 物體的與物體識別有關的所有工作。但是,從網下載的彩色照片中識別真實物體要比識別手寫數字復雜得多。它百倍于手寫數字的類別(1000:10),數百倍于手寫數字的像素(256×256 色:28×28 灰度),是三維場景的二維圖像,需要分割混亂場景,而且每個圖片有多個對象。這樣的情況下,相同類型的卷積神經網絡會起作用嗎?
之后在 ImageNet 2012 年的 ILSVRC 競賽(這個比賽被譽為計算機視覺的年度奧林匹克競賽)中,題目是一個包含大約 120 萬張高分辨率訓練圖像的數據集。測試圖像不顯示初始注釋(沒有分割或標簽),算法要產生指定圖像中存在什么對象的標簽。來自 Oxford、INRIA、XRCE 等機構的先進計算機視覺小組用已有的最好計算機視覺方法應用于這個數據集。通常計算機視覺系統是復雜的多級系統,往往需要在早期階段通過手動調參來優化。
比賽獲勝者 Alex Krizhevsky(NIPS 2012)開發了由 Yann LeCun 開創的深度卷積神經網絡類型。其架構包括 7 個隱藏層(不包括池化層)。前五層是卷積層,后面兩層是全連接層。激活函數在每個隱藏層中被修正為線性單元。這些訓練比 Logistic 單元更快,更有表現力。除此之外,當附近的單元有更強的活動時,它還使用競爭規范化來壓制隱藏的活動,這有助于強度的變化。
有一些技術手段可以顯著提高神經網絡的泛化能力:
從 256×256 圖像中隨機挑選 224×224 塊圖像以獲取更多數據,并使用圖像的左右反射。在測試時,結合 10 個不同的圖像:四個角落加上中間,再加上它們水平翻轉的五個。
使用「dropout」來調整全局連接層(包含大部分參數)的權重。Dropout 指的是隨機移除每個訓練樣本一層中的一半隱藏單元,使其不再過多地依賴其它隱藏單元。
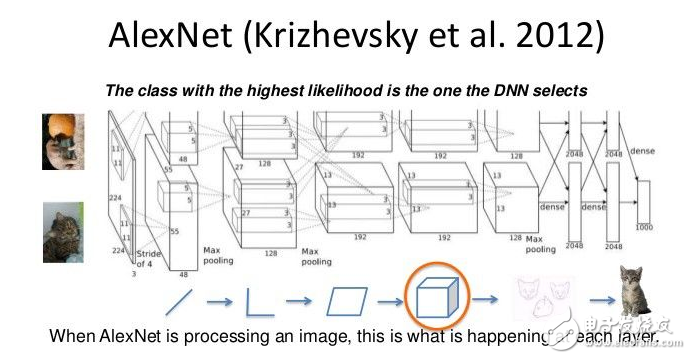
就硬件要求而言,Alex 在 2 個英偉達的 GTX 580 GPU(超過 1000 個快速小內核)上使用了非常高效的卷積網絡實現。GPU 非常適合矩陣乘法,并且具有非常高的內存帶寬。這讓它在一周內訓練了網絡,并在測試時快速結合了 10 個圖像塊的結果。如果我們可以足夠快地交換狀態,我們可以在很多內核上傳播一個網絡。隨著內核越來越便宜,數據集越來越大,大型神經網絡將比老式計算機視覺系統發展得更快。
3. 循環神經網絡
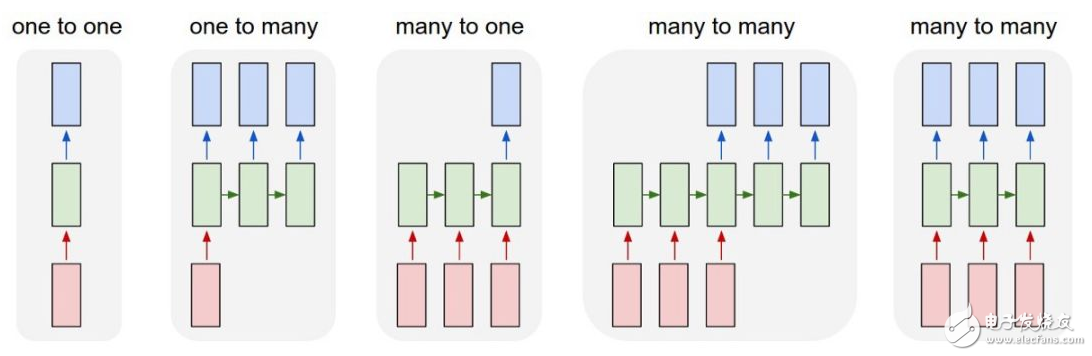
為了理解循環神經網絡,我們需要對序列建模進行簡要概述。當機器學習應用于序列時,我們經常希望將輸入序列轉換為不同域中的輸出序列;例如,將一系列的聲壓轉換成單詞序列。當沒有單獨的目標序列時,我們可以通過嘗試預測輸入序列中的下一項作為網絡的學習目標。目標輸出序列是輸入序列的下一步。比起試圖根據一個圖片的其他像素來預測一個像素或根據圖像的其余部分來預測一個部分,這樣似乎更自然。預測序列中的下一項模糊了有監督學習和無監督學習之間的區別。它使用專為監督學習而設計的方法,但它不需要單獨的目標數據。
無記憶模型是這個任務的標準方法。具體而言,自回歸模型可以通過使用「延遲抽頭」從固定數量的前幾項預測下一項,而且前饋神經網絡是使用一層或多層非線性隱藏單元的廣義自回歸模型。但是,如果我們給生成模型一些隱藏的狀態,使這個隱藏的狀態內部是動態的,我們就會得到一個更有趣的模型:它可以長時間地將信息存儲在隱藏狀態。如果隱狀態的動態從隱狀態中生成輸出是有噪聲的,我們將永遠無法知道它確切的隱藏狀態。我們所能做的是推斷隱狀態矢量空間的概率分布。這種推斷只適用于 2 種隱藏狀態模型。
循環神經網絡是非常強大的,因為它們結合了兩個屬性:1)分布式隱狀態,允許其有效地存儲大量有關過去的信息; 2)非線性動態,使他們能夠以復雜的方式更新隱狀態。有了足夠的神經元和時間,RNN 可以計算任何計算機可以計算出來的東西。那么 RNN 可以表現什么樣的行為呢?它們可以振動,可以穩定在點吸引子,從而表現地很混亂。還可以通過使用隱狀態的不同子集執行許多不同的小程序,每個小程序捕獲一塊知識,而且所有的這些都能并行運行并以更復雜的方式交互。
然而,RNN 的計算能力使它們很難訓練。由于梯度爆發和梯度消失,訓練一個 RNN 是相當困難的。當我們進行多層反向傳播時,梯度的大小會發生什么變化?如果權重很小,則梯度將指數縮小。如果權重很大,梯度將成指數增長。典型的前饋神經網絡可以應付這些指數效應,因為它們只有很少的隱藏層。然而,在訓練長序列的 RNN 中,梯度很容易爆炸或消失。即使初始權重選的很好,也很難檢測到依賴于多個時間步長前的輸入的當前目標輸出,所以 RNN 難以處理序列中的長程依賴。
基本上有 4 種有效的方法來學習 RNN:
長短期記憶:將 RNN 用于長期記憶值的小模塊。
Hessian Free 優化:通過使用酷炫的優化器來處理梯度消失問題,該優化器可以檢測具有更小曲率的微小梯度。
回聲狀態網絡:通過謹慎地初始化層之間的連接(輸入 ->隱層、隱層 ->隱層、輸出 -> 隱層),確保隱藏狀態有巨大的弱耦合震蕩存儲,可以通過輸入選擇性地驅動這些振蕩器。
利用動量進行良好的初始化:像回聲狀態網絡一樣進行初始化,然后使用動量學習所有連接。
4. 長短期記憶網絡
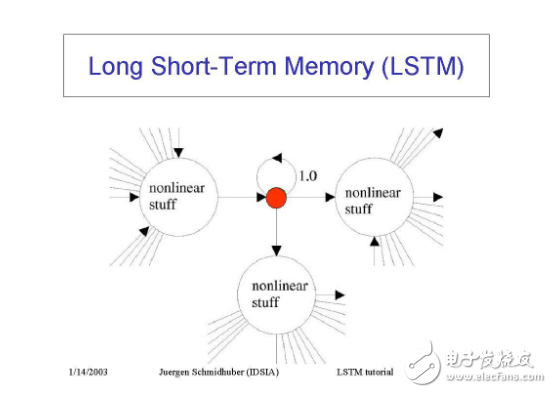
Hochreiter 和 Schmidhuber(1997)通過構建長短期記憶網絡,解決了獲取 RNN 長時間記憶(如數以百計的時間步長)的問題。他們使用具有乘法相互作用的邏輯和線性單元來設計存儲器單元。每當「寫入」門打開時,信息就會進入單元。當「保持」門打開,信息將在單元中保持。信息可以通過打開「讀取」門而從單元中讀取。
手寫草書識別是一個特別適合 RNN 的任務。輸入是筆尖的(x,y,p)坐標序列,其中 p 表示筆是向上還是向下。輸出是一個字符序列。Graves 和 Schmidhuber(2009)表明,帶有 LSTM 的 RNN 是目前草書識別的最佳系統。簡而言之,其使用一系列小圖像代替筆坐標作為輸入。

5. Hopfield 網絡
循環網絡的非線性單元通常很難分析。它們可以表現為不同的方式:穩定到穩定的狀態,振蕩,或遵循不可預測的混沌軌跡。一個 Hopfield 網絡由二元門限單元組成,它們之間有連續的連接。1982 年,John Hopfield 認識到,如果連接是對稱的,就有一個全局能量函數。整個網絡的每個二進制「結構」都有能量,而二進制閾值的決策規則使網絡可以得到能量函數的最小值。利用這類計算的一種簡潔方法是使用記憶作為神經網絡的能量最小值。使用能量最小值來表示記憶從而內存可尋址。可以只知道一個項目的部分內容來訪問這個項目。這對硬件損壞是極大的。
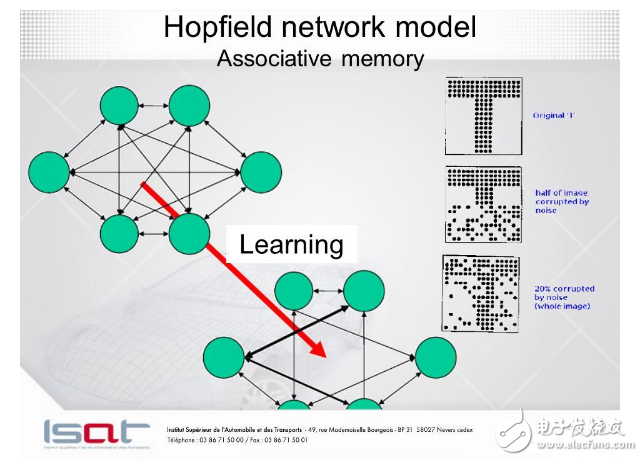
每當記憶一次配置,我們希望創造一個新的能量最小值。但是,如果在中間位置附近有兩個最小值怎么辦呢?這限制了 Hopfield 網絡的容量。那么如何增加 Hopfield 網絡的容量呢?物理學家認為他們已知的數學知識可以解釋大腦的工作機制。物理學期刊上發表了許多關于 Hopfield 網絡及其存儲容量的論文。最終,Elizabeth Gardner 認為,有一個更好的存儲規則——使出權重的「渾身解數」。這不是一次性存儲向量,而是多次循環訓練集,并利用感知機收斂過程來訓練每個單元,使其具有正確的狀態,給定該向量中所有其他單元的狀態。統計學家稱這種技術為「偽可能性」。
Hopfield 網絡還有另一個計算功能。我們不再用網絡來存儲記憶,而是用它來構建感官輸入的信息。用可見單元表示輸入,用隱藏節點的狀態來表達輸入節點的信息,用能量表示信息的不好(低的能量狀態來表達一個好的 interpretation)。
6. 玻爾茲曼機網絡
玻爾茲曼機是一種隨機遞歸神經網絡。它可以被看作是 Hopfield 網絡隨機生成的對應物。它是第一個能夠學習內部表示的神經網絡之一,能夠表示并解決難的組合問題。
玻爾茲曼機學習算法的學習目標是最大化玻爾茲曼機分配給訓練集中二進制向量概率的乘積。這等同于最大化玻爾茲曼分配給訓練向量的對數概率之和。也就是說,如果我們做了如下的事情,最大化我們得到 N 個訓練案例的概率:1)讓網絡在沒有外部輸入的情況下在不同時間穩定分布; 2)每次采樣一次可見向量。
2012 年,Salakhutdinov 和 Hinton 提出了玻爾茲曼機的高效小批量學習程序。
對于正相位,首先將隱藏概率初始化為 0.5,將可見單元上的數據向量進行鉗位,然后并行更新所有隱藏單元,使用平均場方法并行更新隱藏單元直到收斂。在網絡收斂之后,記錄每個連接的單元對 Pi Pj,并在最小批量中對所有數據取平均。
對于負相位:首先保留一組「幻想粒子」(就是一對 (Si,Sj) 形成的系統?)。每個粒子都有全局配置中的一個值。然后串行更新幾次每個幻想粒子中的所有單元。對于每一個連接的單元,對所有的幻想粒子的 SiSj 取平均。
在普通玻爾茲曼機中,單元的隨機更新需要連續。有一個特殊的體系結構允許更有效的交替并行更新(層內沒有連接,沒有跳層連接)。這個小批量程序使玻爾茲曼機的更新更加并行。這就是所說的深度玻爾茲曼機(DBM),一個缺失很多連接的普通玻爾茲曼機。
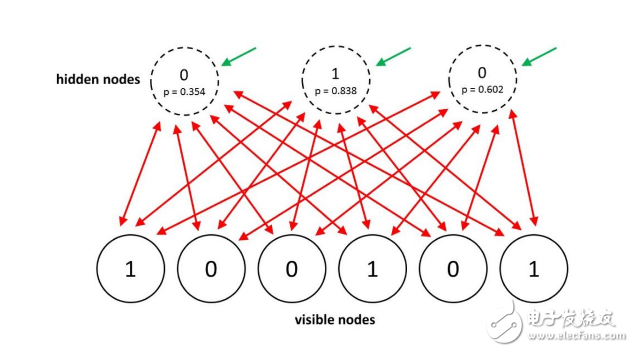
2014 年,Salakhutdinov 和 Hinton 為他們的模型提出了一個升級版,稱之為受限玻爾茲曼機(RBM)。他們通過限制連通性使推理和學習變得更容易(隱藏單元只有一層,隱藏單元之間沒有連接)。在 RBM 中,當可見單元被鉗位時只需要一步就能達到熱平衡。
另一個有效的小批量 RBM 學習程序是這樣的:
對于正相位,首先將可見單元的數據矢量鉗位。然后計算所有可見和隱藏單元對的
對于負相位,也保留一組「幻想粒子」(就是一對 (Vi,Hj) 形成的系統?)。然后交替并行更新幾次每個幻想粒子中的所有單元。對于每一個連接的單位對,所有幻想粒子 ViHj 求平均。
7. 深度信念網絡
反向傳播被認為是人工神經網絡中的標準方法,用于在處理一批數據之后計算每個神經元的誤差貢獻。但是,使用反向傳播存在一些重要的問題。首先,它需要有標簽的訓練數據;而幾乎所有的數據都沒有標簽。其次,學習時間不夠理想,這意味著隱藏層數多的網絡很慢。第三,它可能會陷入局部最小的局面,所以對于深度網絡來說,它們還差得很遠。
為了克服反向傳播的限制,研究人員已經考慮使用無監督的學習方法。這有助于保持使用梯度方法來調整權重的效率和簡單性,還可以用它來對傳感輸入的結構進行建模。特別是,他們調整權重使生成模型產生感官輸入的概率最大化。問題是我們應該學習什么樣的生成模型?可以是像玻爾茲曼機這樣的能量模型嗎?還是由理想化的神經元組成的因果模型?或是兩者的混合?
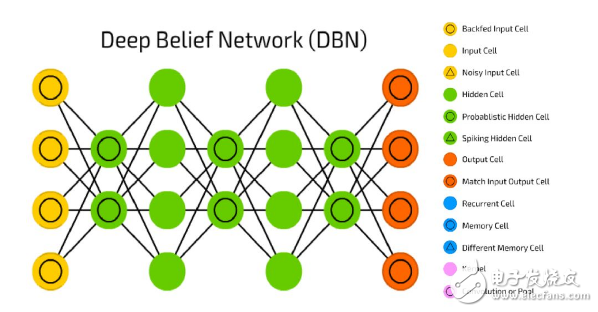
信念網是由隨機變量組成的有向無環圖。使用信念網我們可以觀察到一些變量。我們想要解決 2 個問題:1)推理問題:推斷未觀測變量的狀態; 2)學習問題:調整變量之間的交互作用,使網絡更有可能產生訓練數據。
早期的圖形模型的圖形結構和條件概率是專家定義的。那時,這些圖形連接稀疏,所以研究人員一開始把重點放在做正確的推論,而不是學習上。對于神經網絡來說,學習是關鍵,手寫知識并不酷,因為知識來自于學習訓練數據。神經網絡的目的不在于可解釋性或通過稀疏連接性使其便于推理。不過,還有神經網絡版本的信念網絡。
由隨機二元神經元組成的生成神經網絡有兩種類型:1)基于能量利用對稱連接來連接二元隨機神經元得到玻爾茲曼機; 2)我們通過因果關系在一個有向無環圖中連接二元隨機神經元獲得 SBN。這兩種類型的描述超出了本文的范圍。
8. 深度自動編碼器
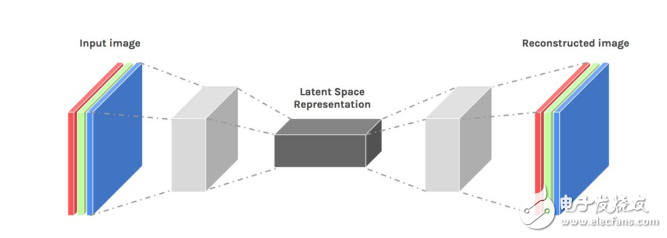
最后,我們來討論深度自動編碼器。深度自動編碼器是非線性降維的非常好的方法,原因如下:它們提供了兩種靈活的映射方式。訓練事例的學習時間是線性的(或更好的),最終的編碼模型相當緊湊和快速。然而,使用反向傳播來優化深度自動編碼器很難。在初始權重較小的情況下,反向傳播梯度消失。現在我們有了更好的方法來優化它們,要么使用無監督的逐層預訓練,要么像回聲狀態網絡那樣謹慎地初始化權重。
對于預訓練任務,實際上有三種不同類型的淺自動編碼器:
受限玻爾茲曼機作為自動編碼器:當我們用一步對比散度訓練受限玻爾茲曼機時,它試圖使重建看起來像數據。它就像一個自動編碼器,但是通過使用隱藏層中的二進制活動來強化正則化。經過最大可能性訓練后,受限玻爾茲曼機不像自動編碼器。我們可以用淺自動編碼器堆棧來代替用于預訓練的 RBM 堆棧;然而,如果淺自動編碼器通過懲罰平方權重而被正規化,那么預訓練就不是有效的(對于隨后的辨別)。
去噪自動編碼器:通過將其許多分量設置為 0(例如輸入的數據丟失的情況),將噪聲添加到輸入向量。他們仍然需要重建這些分量,因此他們必須提取捕獲輸入之間相關性的特征。如果我們使用表示自動編碼器的堆棧,那么預訓練是非常有效的。與 RBM 預訓練一樣好或者更好。由于我們可以很容易地計算目標函數的值,所以評估預訓練也更簡單。它缺乏我們用 RBM 獲得的良好的變分邊界,但這只是理論上的問題。
壓縮自動編碼器:使自動編碼器正規化的另一種方法是盡可能使隱藏單元的活動對輸入不敏感,但是他們不能忽視這些輸入,因為他們必須重建這些輸入。我們通過懲罰每個隱藏活動相對于輸入的平方梯度來達到這個目的。壓縮自動編碼器預訓練時工作得很好。代碼傾向于使一小部分隱藏單元對輸入變化敏感。
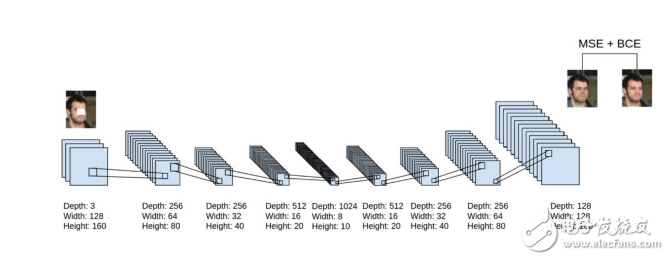
簡而言之,現在有很多不同的方法來進行功能的逐層預訓練。對于沒有大量標簽化的事例的數據集來說,預訓練有助于后續的判別式學習。對于非常大的有標簽的數據集,使用無監督預訓練初始化監督學習中使用的權重進行并不必要,即使對于深度網絡也是如此。預訓練是初始化深度網絡權重的第一個不錯的方法,但現在還有其他方法。但是,如果我們讓網絡很大,我們將再次離不開預訓練!
最后的福利
神經網絡是有史以來最美麗的編程范例之一。在傳統的編程方法中,我們告訴計算機做什么,將大問題分解成計算機可輕松執行的許多精確定義的小任務。相比之下,在神經網絡中,我們不需要告訴計算機如何解決我們的問題,而是讓它通過觀測數據學習,找出解決手頭問題的辦法。
如今,深度神經網絡和深度學習在計算機視覺、語音識別和自然語言處理等許多重要問題上有著出色的表現。它們正在被谷歌、微軟和 Facebook 等公司大規模部署。
我希望這篇文章能幫助你學習神經網絡的核心概念,包括深度學習的現代技術。?
 電子發燒友App
電子發燒友App













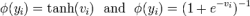











評論